Пример. Задача Найти частные производные второго порядка функции и показать, что она удовлетворяет уравнению. Решение
 Скачать 158.14 Kb. Скачать 158.14 Kb.
|
|
Пример решения типового расчета Задача 1. Найти частные производные второго порядка функции  и показать, что она удовлетворяет уравнению и показать, что она удовлетворяет уравнению  . .Решение. Найдем частные производные первого порядка:  Теперь найдем частные производные второго порядка: 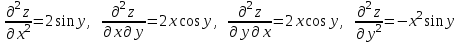 . .Подставим найденные производные в данное уравнение, получим  − тождество. − тождество.Ответ:  . .Задача 2. Дана функция  и точки и точки 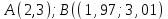 . Вычислить: . Вычислить:точное значение функции  в точке в точке  ; ;приближенное значение функции  в точке в точке  , используя дифференциал; , используя дифференциал;оценить в процентах относительную погрешность; написать уравнение касательной плоскости и нормали к поверхности 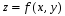 в точке в точке 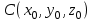 . .Решение. 1. Вычисляем точное значение данной функции в точке  : :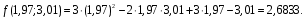 2. Чтобы вычислить приближенное значение данной функции в точке  , за исходную возьмем точку , за исходную возьмем точку 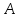 . .Тогда  Находим частные производные данной функции и их значения в точке 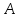 : : Вычисляем значение данной функции в точке 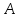 : :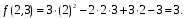 Находим дифференциал и его значение в точке 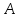 : :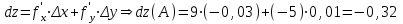 . .Тогда приближенное значение функции в точке  будет равно: будет равно: . .3. Абсолютная погрешность приближенного вычисления равна 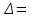  Относительная погрешность 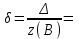 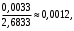 т.е. 0,1%. т.е. 0,1%.Поверхность  задана явно. Будем использовать уравнения касательной плоскости и нормали к поверхности в виде: задана явно. Будем использовать уравнения касательной плоскости и нормали к поверхности в виде: 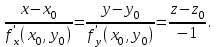 Имеем: 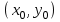 −координаты точки −координаты точки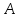 , т.е. , т.е. 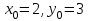 . .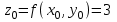 . . 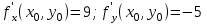 . .Подставляя, получим: уравнение касательной плоскости: 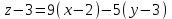 или или  ; ;уравнение нормали к поверхности:  . .Ответ: 1.  4.  − уравнение касательной плоскости; − уравнение касательной плоскости;  − уравнение нормали к поверхности. − уравнение нормали к поверхности.Задача 3. Найти наибольшее и наименьшее значения функции  в замкнутой области в замкнутой области  . . : :  . . 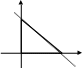  Решение: 1 А Сделаем чертеж области  : : Область  представляет собою ●М представляет собою ●Мвнутреннюю часть треугольника О 0 1 В   . . 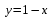 Найдем частные производные, приравняем их нулю и найдем стационарные точки: 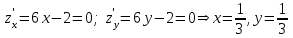 . . Единственная стационарная точка  находится внутри области находится внутри области  . Вычисляем значение функции в этой точке: . Вычисляем значение функции в этой точке: . . Исследуем границу области. Отрезок  . . Тогда  при при 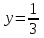 . . Стационарная точка 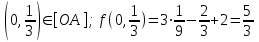 . .Находим значения функции на концах отрезка  : :  . .Отрезок 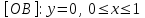 . .Тогда 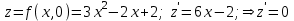 при при 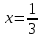 . . Стационарная точка 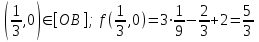 . .Находим значения функции на концах отрезка 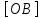 : : 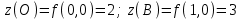 . .Отрезок 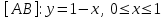 . .Тогда 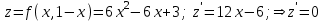 при при  ; ; . .Стационарная точка 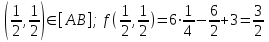 . .Значения функции на концах отрезка  уже найдены. уже найдены.Выбираем из найденных наибольшее и наименьшее значения функции:  . .Ответ:  . .Задача 4. Найти экстремум функции  при условии при условии  . .Решение. Составим функцию Лагранжа:  . .Имеем: 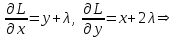  Найдем   . . Значит, ничего сказать о наличии или отсутствии условного экстремум экстремума в точке 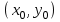 пока нельзя! пока нельзя!Вычислим  : : 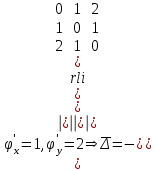 Значит, в точке (2,1) функция  имеет условный максимум, имеет условный максимум,  . .Ответ:  . .Задача 5. Найти градиент скалярного поля 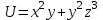 в точке в точке  Решение. Найдем частные производные функции  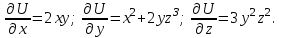 Вычислим значения этих частных производных в точке  Получим:  Значит, 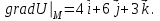 Ответ: 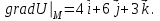 Задача 6. Найти производную скалярного поля 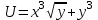 в точке в точке  в направлении единичного вектора в направлении единичного вектора  ; ;наибольшее значение производной функции 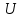 в точке в точке 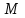 . .Решение. Найдем сначала градиент скалярного поля 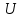 в точке в точке 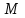 . . Имеем: 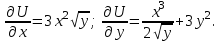  Производная в направлении единичного вектора  равна: равна: Заметим, что 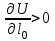 , следовательно, функция , следовательно, функция 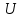 возрастает в направлении вектора возрастает в направлении вектора  , т.е. вдоль оси , т.е. вдоль оси  . .2. Наибольшее значение производной функции 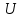 в точке в точке 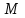 равно модулю градиента: равно модулю градиента: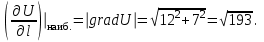 Ответ: 1. 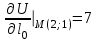 ; 2. ; 2.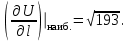 |
