метрология. Мат мод 1. Задача при ограничениях
 Скачать 47.33 Kb.
|
|
Задание 1. Дана исходная задача  при ограничениях  Составить математическую модель симметричной двойственной задачи. По решению двойственной или исходной задачи найти решение другой с использованием основных теорем двойственности. Решение Исходная задача на минимум, следовательно знаки во всех неравенствах должны быть «» - не выполняется. Для получения этого умножим обе части каждого неравенства на –1, получаем  Тогда получаем 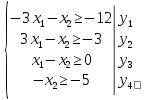  Умножим правые части ограничений на соответствующие переменные двойственной задачи и сложим их, получил целевую функцию  Функция  максимизируется, так как целевая функция исходной задачи минимизируется.Умножим коэффициенты при  в системе ограничений на соответствующие переменные двойственной задачи и сложим их, получим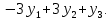 Данная сумма больше или равна коэффициенту при в целевой функции, т.е.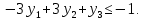 Неравенство имеет вид « 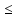 », потому что целевая функция двойственной задачи максимизируется. Аналогично составляем второе ограничение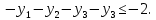 Все переменные двойственной задачи удовлетворяют условию неотрицательности, поэтому что все ограничения исходной задачи неравенства. Окончательно двойственная задача будет иметь вид    Решим исходную задачу графически. Построим следующие прямые     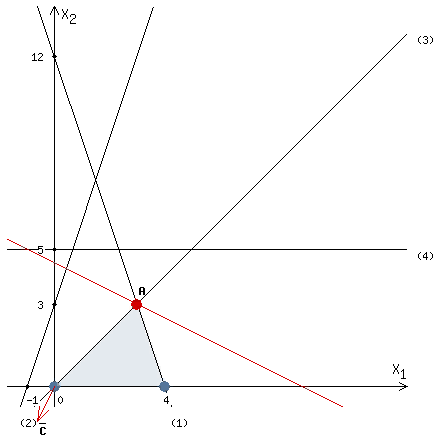 Выделим область допустимых решений. Построенная прямая делит область значений 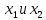 на две подобласти. Для определения подобласти в которой выполняется неравенство подставим в него точку из одного из двух подобластей, если неравенство для этой точки выполняется, то подобласть с этой точкой является областью допустимых решений. Возьмем точку О(3, 1) и подставим ее в заданные неравенства. Допустимые области выделим штриховкой на рисунке. С учетом того, что  получаем область допустимых решений на рисунке.Строим нормаль линий уровня  и одну из линий уровня.Передвигаем линию уровня против направления нормали по области допустимых решений, попадаем в точку А. Для определения ее координат найдем точку пересечения прямых L1 и L3, решая систему уравнений:      Точка минимума 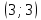 , значение целевой функции  Подставим оптимальное решение 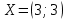 в систему ограничений. Получим, что ограничения (2) и (4) выполняются как строгие неравенства: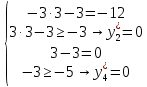 Согласно второй теореме двойственности соответствующие координаты оптимального решения двойственной задачи равны нулю:  и 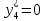 . Учитывая это, из системы ограничений двойственной задачи получим 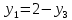  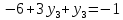    Ответ: 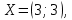  ,  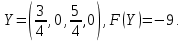|