Контрольная работа по статистике. вариант 10. Задача1

• Название: Задача1
• Анкор: Контрольная работа по статистике
• Дата: 03.07.2021
• Размер: 124.17 Kb.
• Имя файла: вариант 10.docx
• Тип: Задача; #223142

Вариант 10

Задача1.На основе данных задачи 1 варианта 9 проведите группировку страховых организаций по числу договоров страхования. По каждой группе определите количество страховых организаций, а также число страховых случаев, размер страховых взносов, размер страховых выплат в среднем на одну организацию. Результаты группировки представьте в таблице.

Решение:

При 5% выборочном обследовании страховых организаций получены следующие данные:

№ организации	Количество страховых случаев	Размер страховых выплат, д.е.	Число договоров страхования	Размер страховых взносов, д.е.
1	5	25000	100	50000
2	4	17955	95	42750
3	6	31680	110	52800
4	4	10800	85	41650
5	6	36344	118	51920
6	3	21385	65	30550
7	7	54600	143	84000
8	4	13920	60	34800
9	3	10700	70	36400
10	4	11540	82	40180
11	5	17437	94	49820
12	4	12480	78	39000
13	3	12300	63	30240
14	3	10900	87	43065
15	5	9900	96	48480
16	6	47328	136	78880
17	5	31860	120	70800
18	5	20608	115	64400
19	4	16800	112	67200
20	7	31230	128	78080

Определяем оптимальное число групп по формуле:

n =1+ 3,322 lgN,

где N – число единиц совокупности.

n= 1+3,322*lg20=1+3,322*1,301=5,352,

то есть число групп равно 5.

Рассчитаем величину интервала по формуле: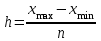

,

где x_max, x_min – наибольшее и наименьшее значение варьирующего признака

h= 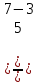=0,8.

Сгруппированные данные будут выглядеть следующим образом (табл.1)

Таблица 1 – Группировка страховых организаций по числу страховых случаев.

Группы страховых случаев	Количество страховых организаций в группе	Число договоров страхования	Размер страховых взносов, д.е.	Размер страховых выплат по группе, д.е.	Размер страховых выплат в среднем на 1 организацию, д.е.
3-3,8	4	285	140255	55285	13821,25
3,8-4,6	6	512	265580	83495	13915,833
4,6-5,4	5	525	283500	104805	20961
5,4-6,2	3	364	183600	115352	38450,667
6,2-7	2	271	162080	85830	42915

Задача 2.

Планом предусмотрено снижение затрат на один рубль товарной продукции на 2,0%. Фактически по сравнению с прошлым годом затраты возросли на 1,8%.

Определите, на сколько процентов фактические затраты на один рубль товарной продукции отличаются от плановых.

Решение:

Планом предусмотрено снижение затрат на один рубль товарной продукции на 2,0% - 98%.

Фактически по сравнению с прошлым годом затраты возросли на 1,8% - 101,8%.

Затраты = 101,8 / 98 = 103,88 % - увеличились фактически затрат по сравнению с планом.
Задача 3.По данным задания 3 варианта 9 определите средний стаж работы мужчин, модальное и медианное значения признака для женщин.

Таблица - Распределения работников предприятия по стажу работы

Стаж работы, лет	Численность работников
	мужчины	женщины
1 2 3 4 5 6 7 8	10 12 28 20 20 12 5 3	5 7 8 9 16 22 17 16
Итого	110	100

Определите средний стаж работы женщин, модальное и медианное значение признака для мужчин, абсолютные и относительные показатели вариации стажа работы для женщин.

Решение:

Рассчитаем средний стаж работы женщин по формуле: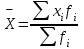

,

где x_i – значение признака;

f_i – частота повторения признака в совокупности;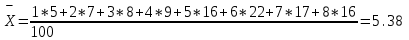

лет.

Средний стаж работы женщин составил 5,38 лет.

Определим абсолютные показатели вариации стажа работы для женщин.

1. 
   Размах вариации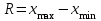
   

,

где x_max, x_min – максимальное и минимальное значение признака.

R=8-1=7.

2. 
   Среднее линейное отклонение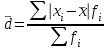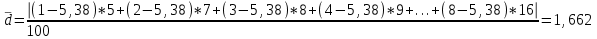
   

,
.

3. 
   Дисперсия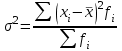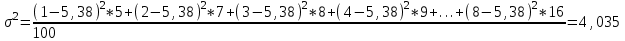
   

,

4. 
   Среднее квадратическое отклонение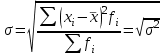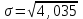
   

,
=2,009.

Определим относительны показатели вариации стажа работы для женщин.

1. 
   Коэффициент осцилляции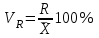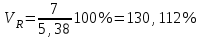
   

,

2. 
   Коэффициент вариации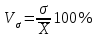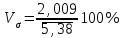
   

,

=37,342%.

Определим модальное и медиальное значение признака для мужчин.

Модой (М₀) называют значение признака, которое встречается наиболее часто у единиц совокупности. Для дискретного ряда модой будет являться вариант с наибольшей частотой.

В нашем примере М₀=3.

Медиана – в дискретном ряду распределения с четным числом вариант – это среднее значение двух серединных вариант.

М_е=4.
Задача 4.Определите, сколько рабочих следует опросить в порядке случайной выборки для определения их среднего заработка, исходя из среднего квадратического отклонения заработка в 230 руб. и допуская ошибку не более 50 руб. с вероятностью 0,997.

Решение:

 = 230 ² = 52900

μ = 52900 / 50 = 1058

∆ = 1058 * 2 = 2116 чел.

Задача 5.По числу вкладов населения в учреждениях сберегательного банка Российской Федерации на начало года имеются следующие данные:

Год	2014	2015	2016	2017
Число вкладов, млн.	141,0	203,7	210,9	234,2

Рассчитайте абсолютные и относительные показатели динамики с постоянной и переменной базами сравнения, а также средние показатели динамики за анализируемый период.

Решение:

Определим среднее число вкладов за ряд лет:

х = (141 + 203,7 + 210,9 + 234,2) / 4 = 197,45 млн.

Рассчитаем абсолютные показатели динамики:

Возьмем 2014г. за постоянную базу.

2015-2014 = 203,7 – 141 = 62,7 млн.

2016-2014 = 210,9 – 141 = 69,9 млн.

2017-2014 = 234,2 – 141 = 93,2 млн.

2015-2014 = 62,7 млн.

2016-2015 = 210,9-203,7 = 7,2 млн.

2017-2016 = 234,2 – 210,9 = 23,3 млн.

Рассчитаем относительные показатели динамики:

2014г.-постоянная база

2015/2014 = 203,7 / 141 = 144 %

2016/2014= 210,9/141 = 149,6%

2017/2014 = 234,2 / 141 = 166,1%

2016/2015 = 210,9/203,7 = 103,5%

2017/2016 = 234,2 / 210,9 = 111,1%


Задача6.Строительно-производственная деятельность двух строительных компаний города характеризуется следующими данными:

Строительная компания	Построено жилья, тыс. м2		Себестоимость 1 м2, тыс. руб.
	2016 г.	2017 г.	2016 г.	2017 г.
1	53	68	25	27
2	179	127	27	29

Рассчитайте индексы себестоимости постоянного состава, переменного состава и структурных сдвигов. Покажите связь между ними.

Решение:
а) индекс себестоимости переменного состава

Рассчитаем средние себестоимости за каждый период:

Средняя себестоимость за отчетный период



Средняя себестоимость за базисный период




Соответственно, индекс себестоимости переменного состава (индекс средних величин) будет представлять собой отношение:


За счет всех факторов себестоимость возросла на 6.63%

б) индекс себестоимости фиксированного (постоянного) состава



За счет изменения структуры себестоимости, средняя себестоимость возросла на 7.6%.

в) индекс влияния изменения структуры услуг на динамику средней себестоимости.


Индекс структурных сдвигов равен отношению индекса переменного состава и индекса фиксированного состава, т.е.:




За счет изменения структуры услуг, средняя себестоимость снизилась на 0.9%.

Кроме этих трех индексов для однородной совокупности может быть рассчитан общий индекс физического объема:



Общий индекс стоимости равен:

I_Q = I_п.c. x I_q = 1.0663 x 0.841 = 0.897

Рассмотрим разложение по факторам абсолютного изменения качественного показателя в однородной совокупности.

Абсолютный прирост средних себестоимости по всем группам будет рассчитываться следующим образом:



Изменение средней себестоимости по всем группам только за счет изменения средней себестоимости будет рассчитываться по формуле:



Аналогичные рассуждения проводятся и для расчета изменения средней себестоимости по всем группам только за счет изменения структуры физического объема:




Очевидно, что общий абсолютный прирост средних себестоимости по всем группам равен сумме факторных изменений: