фыпаыфпа. Задачи оптимизации
 Скачать 116 Kb. Скачать 116 Kb.
|
|
Задачи оптимизации Очень широкий класс задач составляют задачи оптимизации или, как их еще называют, экстремальные задачи. Обычно их решение сопряжено с большим количеством вычислений, что затрудняет их решение вручную. Ниже будут рассмотрены некоторые типы задач оптимизации: решение уравнений с одним неизвестным, задачи линейного программирования и аппроксимация функций. Постановка задачи оптимизации В задачах оптимизации требуется найти значения параметров или функций, реализующих максимум или минимум некоторой зависящей от них величины, например: z = f(x1,x2,…,хn), (3.1) часто при дополнительных условиях-неравенствах: q>i(xux2 x„)<0(z=l,2 т). (3.2) Во многих инженерных и экономических задачах, например, желательно найти максимум меры выполнения или минимум стоимости. Другим приложением задач оптимизации является получение приближенных решений выбором неизвестных значений параметров или функций так, чтобы они давали минимум ошибки. В простейшем случае одной независимой переменной х локальные максимум и минимум функции определяются следующим образом. Действительная функция f(x), определенная при х = а, имеет в точке а (локальный) минимум или (локальный) максимум f(а), если существует такое положительное число δ, что при всех Δх = х - а, для которых выполняются неравенства 0 < |Δх| < δ и существует значение f(a + Δх), соответственно Δf ≡ f(a + Δх) - f(a) < 0 или Δf ≡ f(a + Δx)-f(a) > 0 Максимум и минимум функции объединяются общим названием экстремума функции. Определение локальный подчеркивает тот факт, что понятие экстремума связано лишь с достаточно малой окрестностью точки а. При решении оптимизационных задач важно нахождение не локальных экстремумов, а глобального максимума или глобального минимума (наибольшего или наименьшего значений) функции на промежутке X. Для поиска экстремумов существуют различные методы. Часто случается, что при отыскании максимумов и минимумов функций многих переменных получают сложную систему уравнений, в этих случаях экстремумы находятся численными методами, то есть при помощи последовательного применения метода проб. При этом применение компьютера является практически единственным способом решения задачи. Решение уравнений с одним неизвестным Одним из приложений задач оптимизации является численное решение систем уравнений с одним или несколькими неизвестными вида: f(x) = 0. (3.3) Нахождение корней уравнения вида (3.3) даже в случае алгебраических уравнений выше третьей степени представляет достаточно сложную задачу. Трансцендентные же уравнения чаще всего вообще не имеют аналитического решения. В этих случаях единственным путем является получение приближенных решений, выбором неизвестных значений параметров так, чтобы они давали минимум ошибки некоторой целевой функции (как правило, квадратичной). Обычно используются итерационные методы, когда вначале выбирают некоторое начальное приближение х|0| затем вычисляют последовательные приближения x|j+1| = φ(x|j|) (j = 0,1,2,...). Итерационные методы обеспечивают сходимость таких приближений к искомому значению х. Упражнения 1. Решить уравнение cosx = 0 в диапазоне х € [0; 2]. 2. Решить уравнение 2х2 -3х + 1- 0. 3. Решить уравнение х3 - 3х2 + х = 0. Линейное программирование В случае, когда оптимизируемая целевая функция (3.1) и ограничения (3.2) линейны, задача оптимизации решается методами линейного программирования и обычно называется задачей линейного программирования. Задача линейного программирования заключается в нахождении r переменных x1,x2,…,хr минимизирующих данную линейную функцию (целевую функцию): Z = f(x1,x2,…,хr) ≡ с1x1 + с2x2 + … + сrхr. (3.4) (или максимизирующую — Z) при линейных ограничениях-равенствах: ai1x1 + ai2x2 + … + airхr = Ai, где i = 1,2,...,n (3.5) и линейных ограничениях-неравенствах: Aj1x1 + Aj2x2 + … + Ajrхr = Bj, где j = 1,2,...,m. (3.6) Часто задачу линейного программирования (3.4-3.6) сводят путем введения в случае необходимости вспомогательных переменных к стандартной форме (основной задаче линейного программирования). При этом требуется минимизировать целевую функцию: Z = f(x1,x2,…,хr) ≡ с1x1 + с2x2 + … + сnхn. (3.7) при m < n линейных ограничениях-равенствах ai1x1 + ai2x2 + … + ainхn = bi, где i = 1,2,...,m (3.8) и n линейных ограничениях-неравенствах xk ≥ 0, где k = 1,2,…,n. (3.9) Допустимым решением (планом) задачи линейного программирования является упорядоченное множество чисел (x1,x2,…,хn), удовлетворяющих ограничениям (3.8) и (3.9). Это точка в n-мерном пространстве. Допустимое решение, минимизирующее целевую функцию (3.7), называется оптимальным решением (оптимальным планом). Чаще всего оптимальное решение, если оно существует, является и единственным. Однако возможны случаи, когда оптимальных решений бесчисленное множество. Процесс решения задачи линейного программирования обычно состоит из ряда этапов: 1-й этап: осмысление задачи, выделение наиболее важных качеств, свойств, величин, параметров. Это можно делать, составляя схемы, таблицы, графики и т. п.; 2-й этап: введение обозначений (неизвестных). Желательно ограничиваться как можно меньшим количеством неизвестных, выражая по возможности одни величины через другие; 3-й этап: создание целевой функции. Обычно в качестве цели могут выступать максимальная стоимость всего объема продукции, максимальная прибыль, минимальные затраты и т. п. Целевая функция записывается в виде (3.4) или (3.7). 4-й этап: составление системы ограничений, которым должны удовлетворять введенные величины (3.5), (3.6) или (3.8), (3.9). 5-й этап: решение задачи на компьютере. Упражнения 4. Каждому животному нужно ежедневно выдать не менее 6 единиц белков, 8 единиц жиров и 12 единиц углеводов. Есть два вида корма. Одна единица первого корма содержит 21 единицу белка, 2 единицы жира, 4 единицы углеводов и стоит 3 руб. Для второго корма соответствующие цифры следующие: 3, 2, 2 и 2. Составьте математическую модель и найдите оптимальный рацион питания. 5. Продукцию, производимую на заводах А и В, необходимо развезти по предприятиям № 1, № 2. и № 3. Завод А производит 320 единиц продукции, завод В — 380. Предприятие № 1 реализует за сутки 200 кг, № 2 — 280 кг,-№ 3 — 220 кг. Составьте план перевозок продукции, при котором их стоимость будет наименьшей, если стоимость перевозки 1 кг продукции задана таблицей:
6. Завод планирует выпуск двух видов пакеров: неразбуриваемого и разбуриваемого. Для производства разбуриваемого пакера требуется 1 т стали, 2 т полимеров и 1 человеко-день трудозатрат. Для производства неразбуриваемого пакера — 3,5 т стали, 0,5 т полимера и 1 человеко-день трудозатрат. Всего имеется 350 кг стали и 240 кг полимера, 150 человеко-дней трудозатрат. Предусматривается производство не менее 110 пакеров, причем необходимо обеспечить прибыль не менее 1400 тыс.руб. Определите оптимальное количество пакеров каждого вида, если прибыль от реализации разбуриваемого пакера составляет 10 тыс.руб., а неразбуриваемого — 20 тыс.руб. 7. Составьте оптимальный план производства продукции, чтобы стоимость всего объема произведенного была максимальной, если: цена 1 единицы каждой продукции по 20 денежных единиц. На каждую единицу первой продукции расходуется 2 единицы сырья; 4 единицы материалов и 1 человеко-день; второй продукции — соответственно, 2, 3 и 3. Общие объемы ресурсов: фонд рабочего времени — 12; фонд сырья — 16; фонд материалов — 9; цена 1 единицы сырья — 1 денежная единица; цена материалов — 3 денежных единицы. Проанализируйте математическую постановку этой задачи; как увеличить стоимость всей продукции, если можно привлечь дополнительные ресурсы, лишние продавать? 8. Составьте оптимальный план производства, чтобы стоимость всей продукции была максимальной, если:
Общие объемы ресурсов: трудовых — 48; сырьевых — 56; материалов — 72; цена одной единицы сырья — 2 денежные единицы; материалов — 1,5 денежные единицы. Проанализируйте составленный оптимальный план: как можно увеличить стоимость всей продукции, если исходить из возможности свободно распоряжаться ресурсами. Аппроксимация экспериментальных данных На практике часто приходится сталкиваться с задачей о сглаживании экспериментальных зависимостей или задачей аппроксимации. Аппроксимацией называется процесс подбора эмпирической формулы φ(х) для установленной из опыта функциональной зависимости у = f(x). Эмпирические формулы служат для аналитического представления опытных данных. Одна независимая переменная Обычно задача аппроксимации распадается на две части. Сначала устанавливают вид зависимости у = f(x) и, соответственно, вид эмпирической формулы, то есть решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим. Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком заданной функции. После выбора вида формулы определяют ее параметры. Для наилучшего выбора параметров задают меру близости аппроксимации экспериментальных данных. Во многих случаях, в особенности если функция f(x) задана графиком или таблицей (на дискретном множестве точек), для оценки степени приближения рассматривают разности f(xi) - φ(xi) для точек х0,х1,...,хn. Существуют различные меры близости и, соответственно, способы решения этой задачи. Некоторые из них очень просты, быстро приводят к результату, но результат этот является сильно приближенным. Другие более точные, но и более сложные. Обычно определение параметров при известном виде зависимости осуществляют по методу наименьших квадратов. При этом функция φ(х) считается наилучшим приближением к f(x), если для нее сумма квадратов невязок δi, или отклонений «теоретических» значений φ(хi), найденных по эмпирической формуле, от соответствующих опытных значений уi имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение. Используя методы дифференциального исчисления, метод наименьших квадратов формулирует аналитические условия достижения суммой квадратов отклонений (3.10) своего наименьшего значения. Так, если функция φ(х) вполне определяется своими параметрами k,l,m,…, то наилучшие (в указанном смысле (3.10)) значения этих параметров находятся из решения системы уравнений. Например, в простейшем случае, когда функция φ(х) представлена линейным уравнением у = ах + b, система имеет вид: 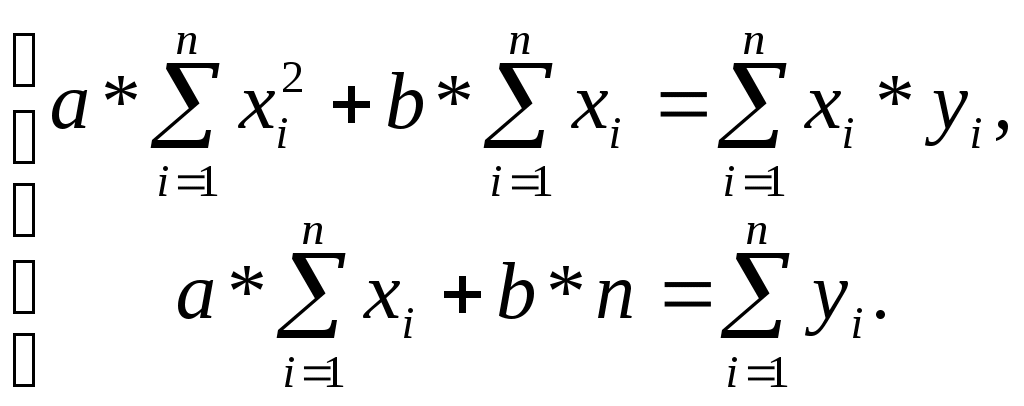 (3.11) (3.11)В простейшем случае задача аппроксимации экспериментальных данных выглядит следующим образом. Пусть есть какие-то данные, полученные практическим путем (в ходе эксперимента или наблюдения), которые можно представить парами чисел (х; у). Зависимость между ними отражает таблица:
На основе этих данных требуется подобрать функцию у = φ(х), которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и по возможности точно отражала общую тенденцию зависимости между х и у, исключая погрешности измерений и случайные отклонения. Это значит, что отклонения yi - yi(xi) в каком-то смысле были бы наименьшими. Например, в смысле (3.10). Выяснить вид функции можно либо из теоретических соображений, либо анализируя расположение точек (хn; уn) на координатной плоскости. Например, пусть точки расположены так, как показано на рис. 3.7. Учитывая то, что практические данные получены с некоторой погрешностью, обусловленной неточностью измерений, необходимостью округления результатов и т. п., естественно предположить, что здесь имеет место линейная зависимость у = ах + b. 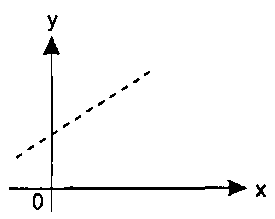 Рис. 3.7. Возможный вариант расположения экспериментальных точек Чтобы функция приняла конкретный вид, необходимо каким-то образом вычислить а и b. Для этого можно решить систему (3.11). Расположение экспериментальных точек в виде кривой на рис. 3.8 наводит на мысль, что зависимость обратно пропорциональна и функцию φ(х) нужно подбирать в виде у = а + b/х. Здесь также необходимо вычислить параметры а и b. 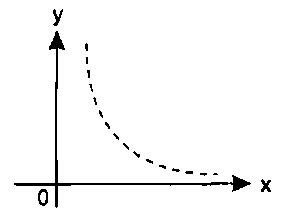 Рис. 3.8. Другой вариант расположения экспериментальных точек Таким образом, расположение экспериментальных точек может иметь самый различный вид, и каждому соответствует конкретный тип функции. Построение эмпирической функции сводится к вычислению входящих в нее параметров, так чтобы из всех функций такого вида выбрать ту, которая лучше других описывает зависимость между изучаемыми величинами. То есть сумма квадратов разности между табличными значениями функции в некоторых точках и значениями, вычисленными по полученной формуле, должна быть минимальна. В MS Excel аппроксимация экспериментальных данных осуществляется путем построения их графика (х — отвлеченные величины) или точечного графика (х — имеет конкретные значения) с последующим подбором подходящей аппроксимирующей функции (линии тренда). Возможны следующие варианты функций: 1. Линейная — у = ах + b. Обычно применяется в простейших случаях, когда экспериментальные данные возрастают или убывают с постоянной скоростью. 2. Полиномиальная — у = а0 + а1х + а2х2 + ... + аnхn, где до шестого порядка включительно (n ≤ 6), аi — константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов (максимумов или минимумов) кривой. Полином второй степени может описать только один максимум или минимум, полином третьей степени может иметь один или два экстремума, четвертой степени — не более трех экстремумов и т. д. 3. Логарифмическая — у = alnx + b, где а и b — константы, In — функция натурального логарифма. Функция применяется для описания экспериментальных данных, которые вначале быстро растут или убывают, а затем постепенно стабилизируются. 4. Степенная — у = bxn, где а и b — константы. Аппроксимация степенной функцией используется для экспериментальных данных с постоянно увеличивающейся (или убывающей) скоростью роста. Данные не должны иметь нулевых или отрицательных значений. 5. Экспоненциальная — у = bеаx, где а и b — константы, е — основание натурального логарифма. Применяется для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируются. Часто ее использование вытекает из теоретических соображений. Степень близости аппроксимации экспериментальных данных выбранной функцией оценивается коэффициентом детерминации (R2). Таким образом, если есть несколько подходящих вариантов типов аппроксимирующих функций, можно выбрать функцию с большим коэффициентом детерминации (стремящимся к 1). Для осуществления аппроксимации на диаграмме экспериментальных данных необходимо щелчком правой кнопки мыши вызвать выплывающее контекстное меню и выбрать пункт Добавить линию тренда. В появившемся диалоговом окне Линия тренда на вкладке Тип выбирается вид аппроксимирующей функции, а на вкладке Параметры задаются дополнительные параметры, влияющие на отображение аппроксимирующей кривой. Упражнения 9. Построить функцию, наилучшим образом отражающую данную зависимость:
10. Уровень дефицита бюджета на предприятиях складывался следующим образом:
Построить функции, наилучшим образом отражающие зависимости дефицита бюджета от времени в обеих странах. 11. Количество вложенных в производство средств и полученная в результате прибыль соотносятся следующим образом:
Запишите аналитическую зависимость между х и у. Проанализируйте полученный ответ. Каковы перспективы предприятия? Какая будет прибыль, если вложить 10,0 единиц? Сколько надо вложить средств, чтобы получить прибыль 100,0 единиц? Несколько независимых переменных В тех случаях, когда аппроксимируемая переменная у зависит от нескольких независимых переменных х1,х2,…,хn, у = f(х1,х2,…,хn), подход с построением линии тренда не дает решения. Здесь могут быть использованы следующие специальные функции MS Excel: Упражнения 12. В условиях примера 3.8 найти параметры аппроксимирующего уравнения и оценить его точность. 13. В условиях примера 3.7 найти расчетные значения интенсивности излучения для следующих значений х1 и х2:
14. Застройщик оценивает стоимость группы небольших офисных зданий в традиционном деловом районе. Оценку цены офисного здания в заданном районе застройщик предполагает осуществлять на основе следующих переменных: у — оценочная цена здания под офис, x1 — общая площадь в квадратных метрах, х2 — количество офисов, х3 — количество входов, х4 — время эксплуатации здания в годах. Предполагается, что существует линейная зависимость между каждой независимой переменной (х1, х2, х3 и х4) и зависимой переменной (у), то есть ценой здания под офис в данном районе. Застройщик наугад выбирает 11 зданий из имеющихся 1500 и получает следующие данные:
Здесь «полвхода» (1/2) означает вход только для доставки корреспонденции. Найти параметры аппроксимирующего уравнения. 15. В условиях упражнения 14 с помощью функции ТЕНДЕНЦИЯ определить оценочную стоимость здания под офис в том же районе, которое имеет площадь 2500 квадратных метров, три офиса, два входа, зданию 25 лет. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
