1.3 Механика. Законы сохранения Замкнутой называется такая система тел, для которой равнодействующая всех внешних сил равна нулю. С их точки зрения, изолированная система всегда

• Название: Законы сохранения Замкнутой называется такая система тел, для которой равнодействующая всех внешних сил равна нулю. С их точки зрения, изолированная система всегда
• Анкор: 1.3 Механика.docx
• Дата: 14.10.2021
• Размер: 125.88 Kb.
• Имя файла: 1.3 Механика.docx
• Тип: Закон; #247894

1.3. Законы сохранения

1. 
   Замкнутой называется такая система тел, для которой равнодействующая всех внешних сил равна нулю. С их точки зрения, изолированная система всегда является замкнутой, но не наоборот. Понятие замкнутой системы является идеализацией, так как гравитационные силы распространяются при любых расстояниях между объектами.
   
2. 
   Зако́н сохране́ния и́мпульса (зако́н сохране́ния количества движения) — закон, утверждающий, что сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю^[1]. В основе закона сохранения момента импульса лежит изотропия пространства, т. е. одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат).
   
3. 
   Центр масс движется так, как двигалась бы материальная точка, масса которой равна массе системы, под действием силы, равной сумме всех внешних сил, действующих на систему
   
4. 
   физике консервати́вные си́лы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки^[1]. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0. Каждое тело создает вокруг себя поле, которое проявляет себя именно воздействием на другие тела. Силы, работа которых не зависит от пути, по которому двигалось тело, а зависит от начального и конечного положения тела называются консервативными. Обозначим A – работа консервативных сил, по перемещению тела из т. 1 в т. 2 (рисунок 5.2) Рисунок 5.2 . A 1a 2  A 1b 2  A 1l 2  A 12 Изменение направления движения на противоположное – вызывает изменение знака работы консервативных сил. Отсюда следует, что работа консервативных сил вдоль замкнутой кривой равна нулю: d 0   12  21  12  12  S F r A A A A (5.2.1) Интеграл по замкнутому контуру S, – называется циркуляцией вектора  S Fdr  F
   
5. 
   Механическая работа (A) — физическая величина, равная произведению вектора силы, действующей на тело, и вектора его перемещения: (A=\vec{F}\vec{S}).
   
6. 
   Механической энергией тела в физике называют сумму кинетической и потенциальной энергий этого тела.
   
7. 
   Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости. E K= m v 2. Кинетическая энергия - энергия движения тела. При нулевой скорости она равна нулю.
   
8. 
   Потенциальная энергия зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы и описывающая взаимодействие элементов системы. Ep=mgh
   
9. 
   Потенциальная энергия – это способность тела совершить работу за счет расположения материальных точек, составляющих систему. Действительно, для тела, которое падает под действием силы тяжести, работа совершается за счет взаимного расположения Земли и тела. В случае силы упругости, работа совершается за счет взаимного расположения молекул внутри телf
   
10. 
    –
    
11. 
    Закон сохранения механической энергии: В изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется. Е = Е к + Е п = const. Закон сохранения механической энергии является частным случаем общего закона сохранения энергии: энергия не создаётся и не разрушается, а преобразуется из одной формы в другую.
    
12. 
    Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение.
    
13. 
    Момент импульса Lz относительно неподвижной оси z равен проекции на эту ось вектора момента импульса относительно произвольной точки О, лежащей на этой оси.
    
14. 
    Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел, которая остается постоянной, пока на систему не воздействуют моменты внешних сил. В основе закона сохранения импульса лежит однородность пространства, т. е. одинаковость свойств пространства во всех точках (симметрия по отношению к сдвигу начала координат).
    
15. 
    Гироскопический эффект – это удержание (устойчивость) оси вращения объекта в пространстве. Этот эффект зависит от массы объекта, угловой скорости и от распределения моментов инерции.
    
16. 
    А=FS=10*3,14*1*2=62,8 Дж
    
17. 
    E(k)=m(v^2)/2=3 кг*(4м/c)^2/2=(3*16)/2=48/2=24 Дж.
    
18. 
    W=mgh=> h= w\mg= 200\0.8*10=25m
    
19. 
    А = ΔEk = m * V12 / 2 - m * V22 / 2. A=64дж
    
20. 
    Энергия "до"---Е1=0.5*m*(V1)^2
    Энергия "после "----Е2=0.5*m*(V2)^2
    Работа А=dE=E1-E2=
    
21. 
    E(потенц)= (k·x²)÷2. Неизвестно K, найдем через Закон Гука F=kx ⇒k=F÷x. Подставляем в первую формулу и получаем Ep=(F·x)÷2 ⇒ Ep=(0.03·20)÷2 ⇒ Ep=0.3 ДЖ.
    
22. 
    –
    
23. 
    A=k*x*x/2=k*0.004*0.004/2=0.02
    

k=2500

A=k*x*x/2=2500*0,04*0,04/2=2Дg

24. 
    E=(m/2)*V^2 => E/p= (m/2)*V^2/mV=V/2 =>V=2 E/р=2 * 20/10=4 м/c
    
25. 
    
    

По закону сохранения импульса





(т.к. стенка до взаимодействия покоялась и её импульс  )



Или



Проекция на ось Y



Импульс, который получает стенка после удара об неё шариком



Скорость шарика перед ударом найдём, используя закон сохранения энергии



 



Скорость шарика после удара



Высота, на которую поднимется шарик после удара





 

С другой стороны высота подъема после удара



 

Время падения шарика



где t₁ – время падения с высоты h₁,



t₂ – время падения с высоты h₂



Время падения шарика



            Ответ: 

            

26. 
    0.5*F*s=m*g*H
    0.5*F=(m*g*H)/s=(600*10*3)/0.06=300000n 0.5*F -средняя сила.
    
27. 
    V = (60 * 8 + 80 * 2,9) / (60 + 80) = 712 / 140 ≈ 5,09 км/ч.
    
28. 
    m=16*10^3 кг    v=0.6 м/с    x=0.08 м    k=?
    
    m*v²/2=k*x²/2
    k=m*(v/x)²=16*10^3*(0.6/0.08)²=9*10^5 Н/м   (900 кН/м)
    

29.а)

Проекция на ось x:

Скорость ружья после выстрела

30. m1 (масса снаряда) = 2 кг; V1 (скорость полета снаряда) = 300 м/с; m2 (масса неподвижной мишени с песком, V2 = 0 м/с) = 100 кг.

Скорость движения мишени после попадания снаряда определим с помощью закона сохранения импульса: m1 * V1 = V1.2 * (m1 + m2) и V1.2 = m1 * V1 / (m1 + m2).

Расчет: V1.2 = 2 * 300 / (2 + 100) = 600 / 102 ≈ 5,88 м/с.

31. Если движение первого осколка продолжается вдоль той же прямой, то и второйосколок должен двигаться вдоль той же прямой. m=m1+m2; m1+m2; m*v=m1*2*v+m2*u; u=(m*v-2*m1*v)/m2; u=(2*m1*v-2*m1*v)/m1=0; Второй осколок начнет свободное падение с начальной скоростью равной 0.

32. Значит, вся кинетическая энергия перешла в потенциальную и они равны. Eк=mV²/2 Eп=mgh mgh=mV²/2 массы сокращаем gh=V²/2 h=V²/2g h=100/2*10=5м ответ 5 метров.

33. 1) 54 км/ч = 15 м/с Полезная мощность: Nпол = F*V = 15*F. 2) КПД = Nпол / N пот 0,75 = 15*F / 600 000 15*F = 450 000 F = 450 000 / 15 = 30 000 Н или 30 кН.

34.  A=m*g*h=2*10*1=20 Дж.

35. Закон сохранения импульса: m1 v1 + m2 v2 = m1 V1 + m2 V2
Закон сохранения энергии: m1 v1^2/2 + m2 v2^2/2 = m1 V1^2/2 + m2 V2^2/2

В нашем случае система немного проще:
m1 v1 = m1 V1 + m2 V2
m1 v1^2/2 = m1 V1^2/2 + m2 V2^2/2

Выражаем V1 из первого уравнения: V1 = v1 - (m2/m1) V2, подставляем во второе, приводим подобные, решаем относительно V2:
V2 = 2 m1 v1 / (m1 + m2)
V1 = v1 - 2 m2 v1 / (m1 + m2)

Подставляя численные значения, получаем ответ:
V1 = - 6 м/с (знак "минус" означает, что первый шар покатится в обратную сторону)
V2 = 4 м/с

36. Закон сохранения импульса (ЗСИ): импульс системы остается постоянным при любых взаимодействиях внутри системы:

 а) 

Проекция на ось x:



Скорость тел после соударения

 

 

б) 

Проекция на ось x:



Закон сохранения энергии



 

Скорость тел после соударения

                                               

                                               

37.

Закон сохранения импульса: импульс системы остается постоянным при любых взаимодействиях внутри, или импульс системы снаряд – орудие до выстрела равен импульсу этой ситсемы после выстрела:

                   (1)

Проекция на ось x:

                  (2)

 

 

Скорость орудия после выстрела

                     (3)

 

Кинетическая энергия снаряда

                    (4)

Скорость снаряда

                     (5)

 

(5) в (3)



Кинетическая энергия орудия



38. A = k*X2^2/2  - k*X1^2/2=k/2(X2^2 - X1^2)=
800/2* (14^2 - 8^2)*10^-4=5,28 Дж

39-

40.-

41.

42. Кинетическая энергия вращающегося тела



 

Угловая скорость    

       

Момент инерции



Момент импульса L вала


43. Т.к. шар участвует в поступательном и вращательном движении одновременно, то полная кинетическая энергия шара



где кинетическая энергия поступательного движения



 

кинетическая энергия вращательного движения



Момент инерции шара



Связь линейной и угловой скорости



Угловая скорость связана с частотой вращения



Тогда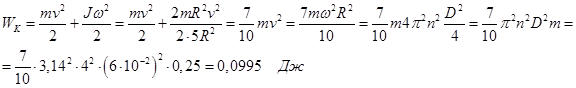


44. Т.к. обруч участвует в поступательном и вращательном движении одновременно, то полная кинетическая энергия обруча



где кинетическая энергия поступательного движения



 

кинетическая энергия вращательного движения



Момент инерции обруча



Связь линейной и угловой скорости



Тогда



Аналогично для диска:

Момент инерции диска





Т.к. по условию m₁ = m₂, то


44. акон сохранения момента импульса





  I₁ – момент инерции платформы с человеком, стоящим на её краю,    

  I₂ – момент инерции платформы с человеком, стоящим в центре,

платформы, ϖ₁ и ϖ₂ – соответствующие угловые скорости.

                                   



Учитывая, что



найдём