кр редуктор. Зап2. 0,98 кпд муфты 1,стр 6,табл 1 0,97 кпд цилиндрической передачи 1,стр 6,табл 1
 Скачать 0.97 Mb. Скачать 0.97 Mb.
|
1 2    1.4 Потребная мощность электродвигателя (мощность с учетом вредных сил сопротивления): Рэд= Рэд =5/0,72=6,94 кВт. 1.5 Частоты вращения барабана (третьего вала): 1.6 Определяем частоту вращения электродвигателя: где По значению Рэди 1.7 Уточнение передаточных чисел редуктора где 1.8 Определение вращающих моментов на валах привода. 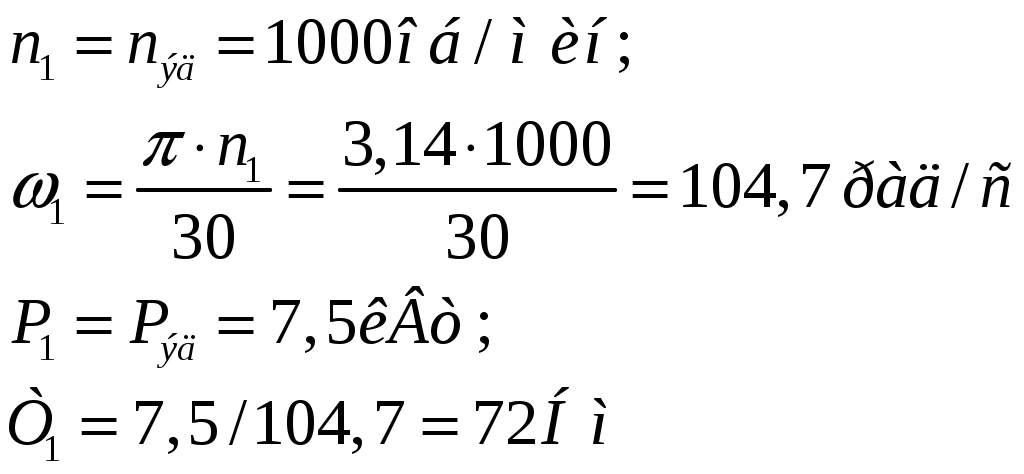 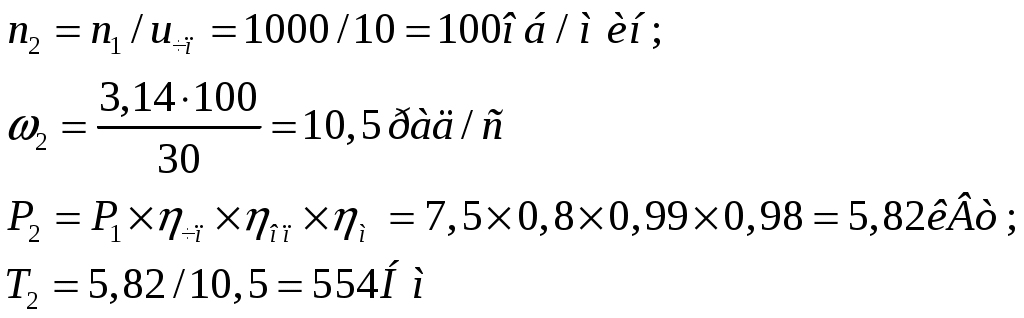 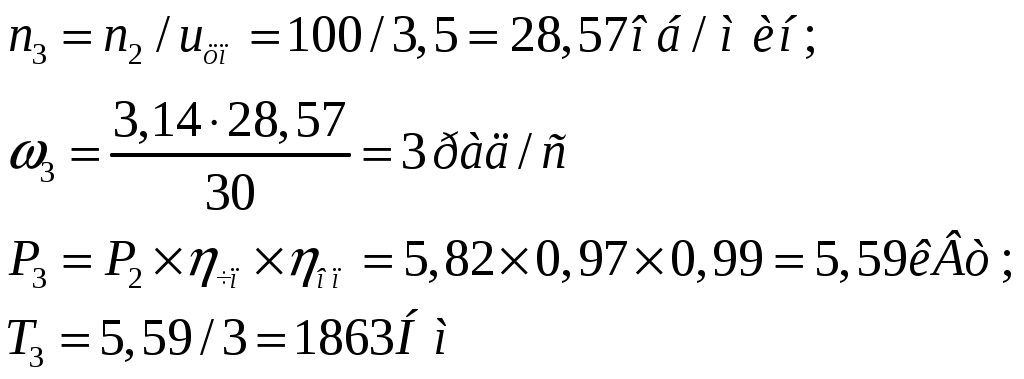 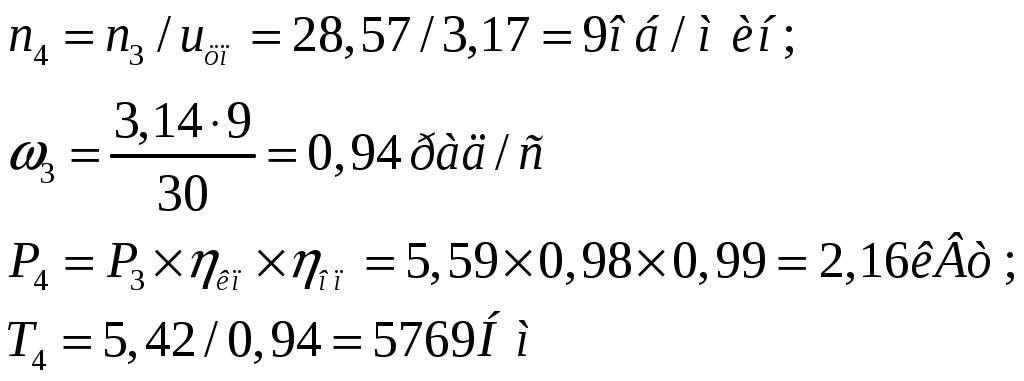 2. РасчЁт редуктора 2.1. Расчёт червячной ступени. Исходные данные: и=10; Т=554Нм; п=100мин-1. График нагрузки 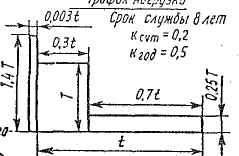 2.1.1. Выбор твёрдости, термической обработки и материала колес. Для колес из бронзы, имеющей предел прочности В>300 МПа, опасным является заедание, и допускаемые напряжения назначают в зависимости от скольжения Vs без учёта количества циклов нагружения. В нашем случае (по таблице 27 из [2]) в зависимости от материала червяка и скорости скольжения без учёта количества циклов нагружения принимаем [H]2=173 МПа. Определим вращающие моменты на валах: Т31 = 1,4 ТН = 1,4 554 = 775,6(Нм); Т32 = ТН = 554 (Нм); Т33 = 0,25ТН = 0,25554 = 138,5 (Нм); Определим время действия вращающих моментов: Выбираем скорость скольжения и материал. Применяют бронзу БрО10Н1Ф1 1 группа стали [1,стр 31 табл. 2.14] [σ]Т = 165 МПа; σв = 385 МПа. 2.1.2. Определяем допускаемые напряжения изгиба: [σ]Нmax = 4 [σ]Т= 4 ∙ 165 = 660 МПа; [σ]Fmax =0,8 [σ]Т= 0,8 ∙ 165 = 132 МПа. 2.1.3 Определяют межосевое расстояние где Ка – коэффициент для косозубых передач, Ка = 610 [1,стр 31]; Кнв – коэффициент нагрузки Кнв = 1 [1,стр 31 табл 2.15] принимаем аW =120мм. 2.1.4. Число зубьев колеса. По таблице выбираем число зубьев червяка Z1 = 4. Z2 = Z1 · Uч = 4 · 10 = 40. 2.1.5. Модуль передачи: Принимаем m=5мм. 2.1.6. Коэффициент диаметра червяка: Принимаем q = 8 . 2.1.7. Коэффициент смещения: 2.1.8. Геометрические параметры червяка Диаметры червяка: d1 = q · m = 8 · 5 = 40 мм; da = d1 + 2m = 40 + 10 = 50 мм; df = d1 - 2,5m = 40 – 12,5 = 27,5 мм. Диаметры колеса: d2= m · z2 = 5 · 40 = 200 мм; dа2 = d2 + 2m(1 + x) = 200 + 10 ∙ (1 – 0) = 210 мм; df2 = d2 - 2m(1,2 - x) = 200 – 10 ∙ (1,2 + 0) = 188 мм. 2.1.9. Проверка зубьев колёс по контактным напряжениям. 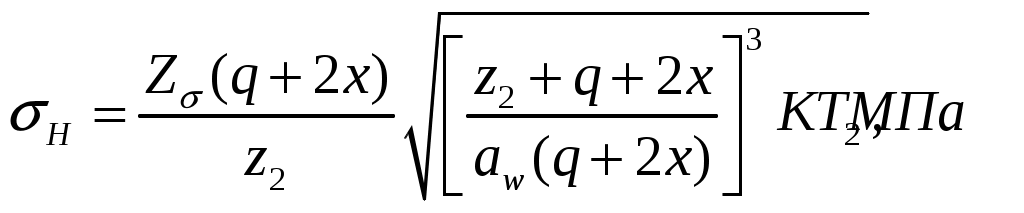 ; [1,стр 34] ; [1,стр 34]где Zσ = 5350 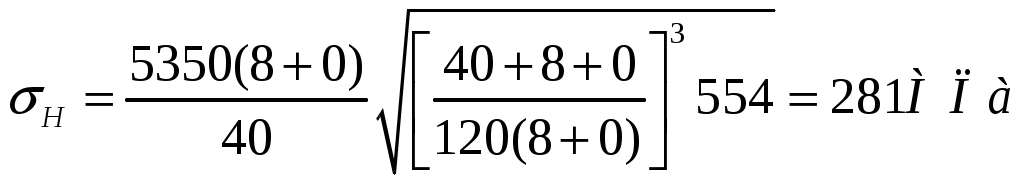 МПа; МПа; 2.1.10. Силы в зацеплении. Окружная сила червяка: Радиальная сила: Окружная сила колеса: Радиальная сила: 2.1.11. Проверка зубьев колёс по напряжения изгиба: σϜ = где σϜ = 2.2. Расчёт цилиндрической ступени. Исходные данные: и=3,5; Т3=1863Нм; п3 = 28,57мин-1. 2.2.1 Определение допускаемых контактных напряжений для шестерни и колеса Примем в дальнейшем, что величины, имеющие индекс «1», относятся к шестерни, а с индексом «2» - к колесу. Определение допускаемых контактных напряжений ГОСТ 21354–75: где: нагружения; Вычислим Вычислим 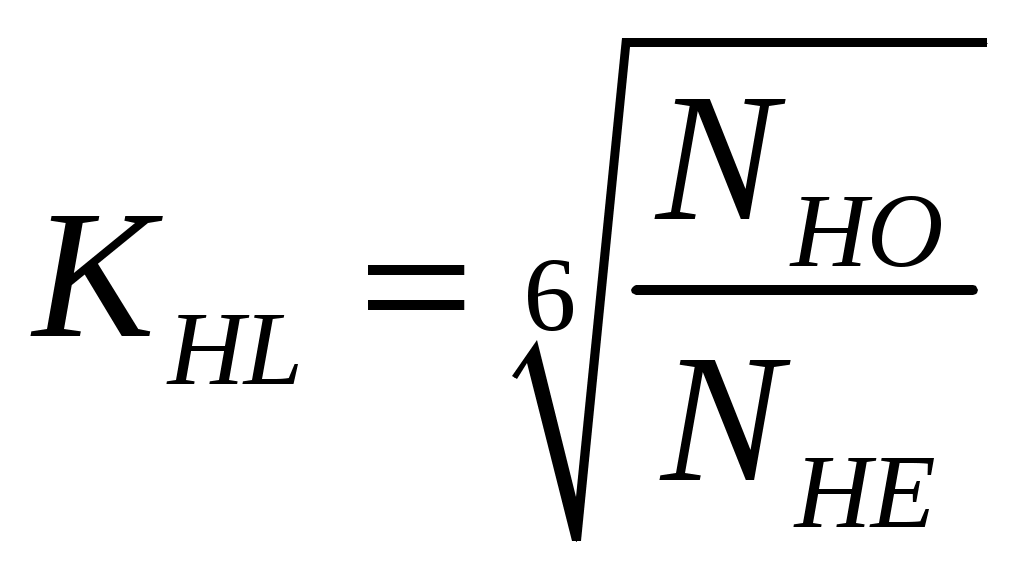 , ,где передачи. Вычислим Вычислим 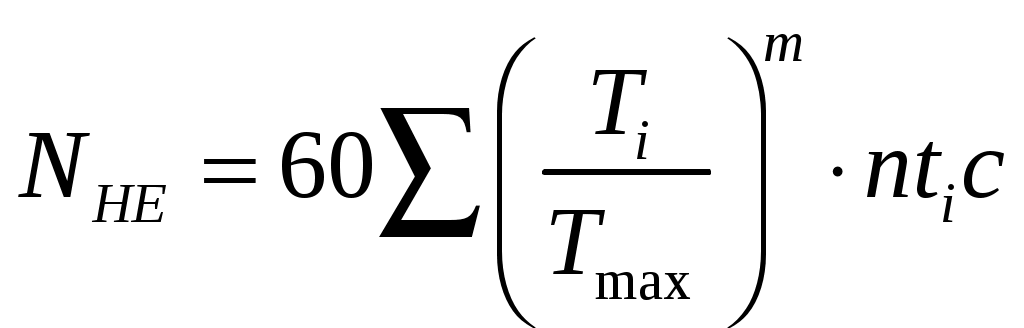 где: Вычислим 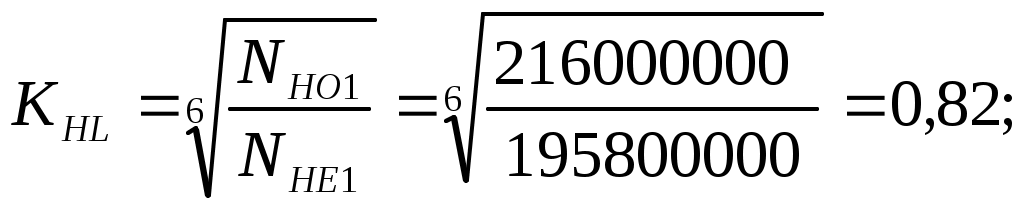 принимаем Определим допускаемые контактные напряжения колеса: Определение допускаемых напряжений при расчете зубьев на изгиб Допускаемые напряжения изгиба где Вычислим Вычислим 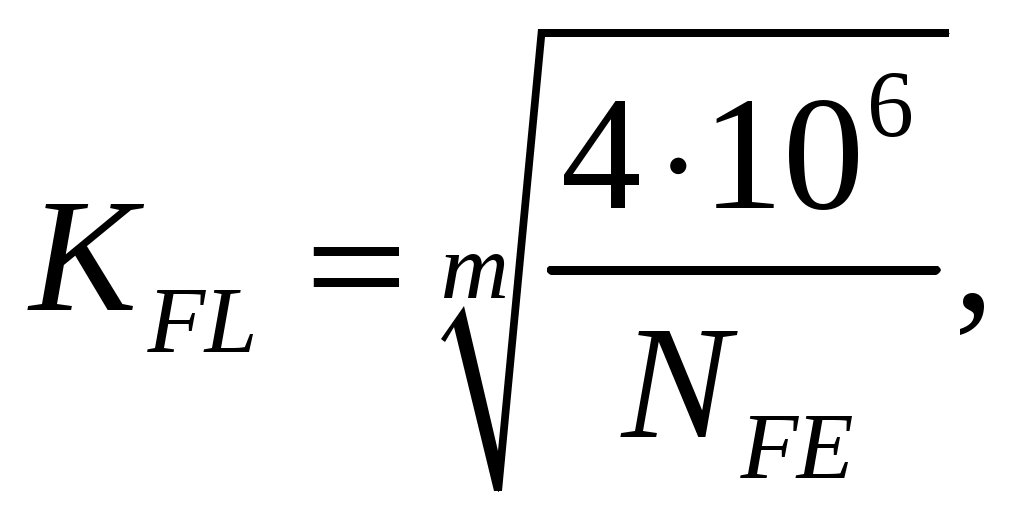 где передачи. Т.к. Вычислим число циклов за весь срок службы передачи только при показателе степени Подставим полученные значения в формулу нахождения 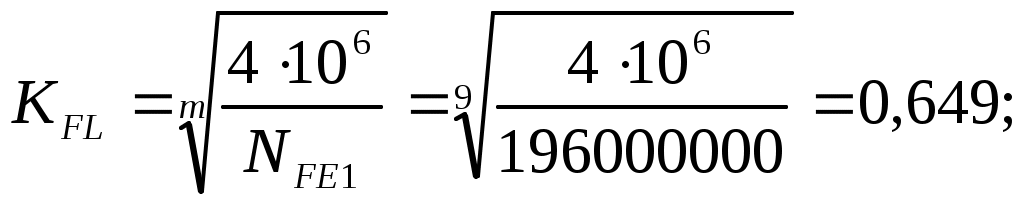 Значения Примем Подставим найденные значения нахождения Определение предельно допускаемых контактных напряжений При кратковременных нагрузках (расчет на пиковые нагрузки) предельно допускаемые напряжения определяются по эмпирическим зависимостям: Определение предельно допускаемых напряжений изгиба При кратковременных нагрузках (расчет на пиковые нагрузки) предельно допускаемые напряжения определяются по эмпирическим зависимостям. 2.2.2 Расчет межосевого расстояния 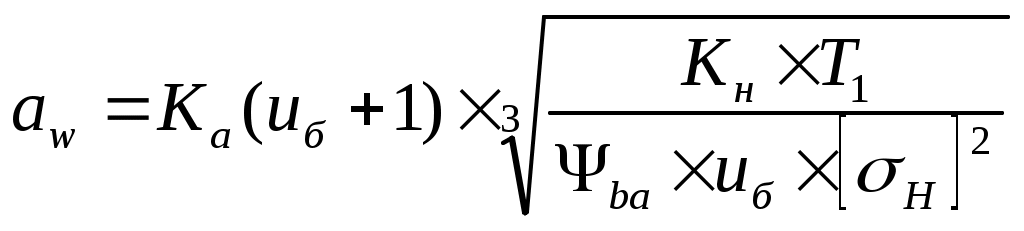 где: колёса расположены симметрично , то ; нагрузки между зубьями, нагрузки по ширине зубчатого венца, Округляем до стандартного значения 190 мм ( из ГОСТ 6639-69) [ 1, с.410] 2.2.3 Определение модуля передачи m. 2.2.4 Суммарное число зубьев. 2.2.5 Число зубьев шестерни и колеса. 2.2.6 Фактическое передаточное отношение. где: 2.2.7 Определение геометрических размеров колес. 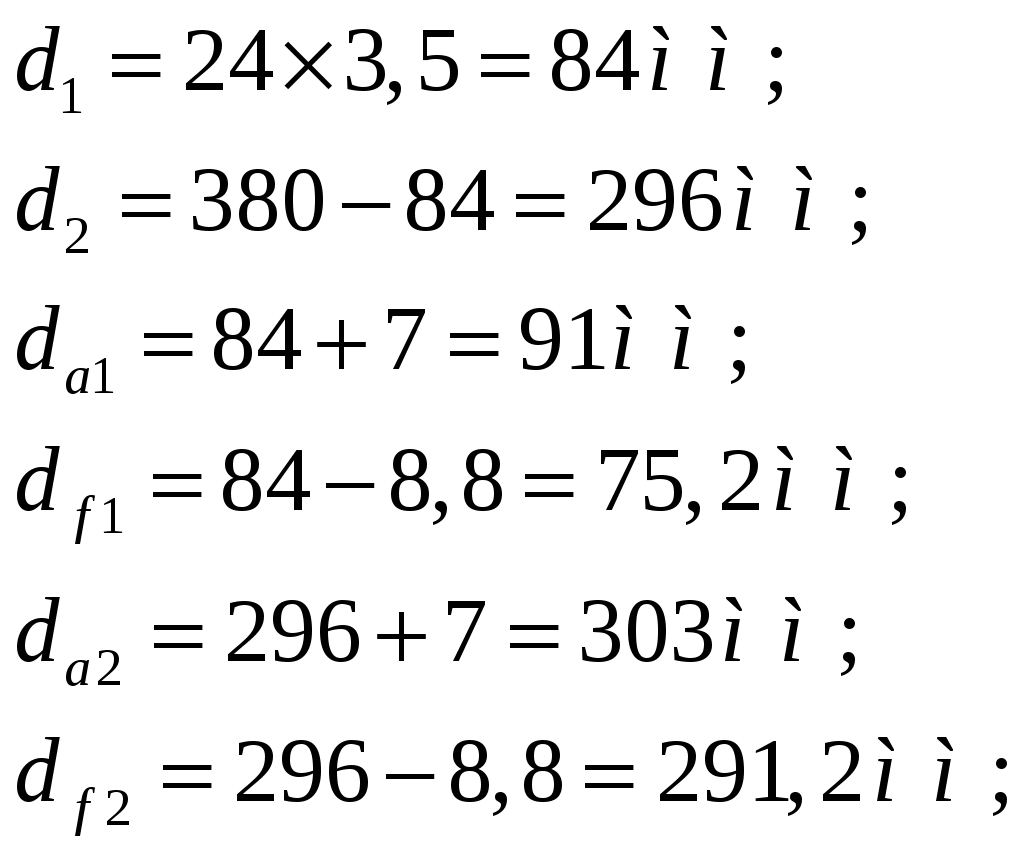 2.2.8 Проверка зубьев колес по контактным напряжениям. 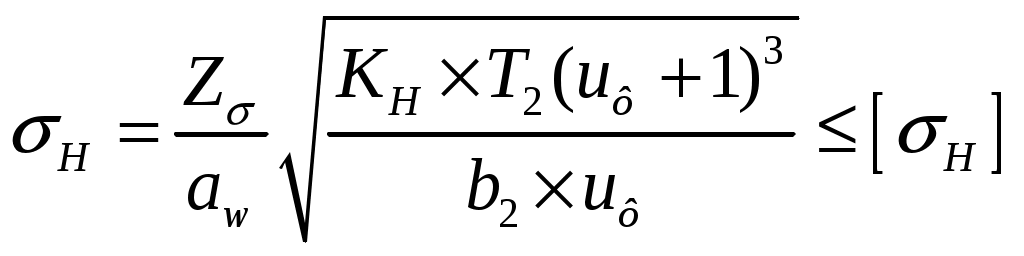 Zσ = 9600 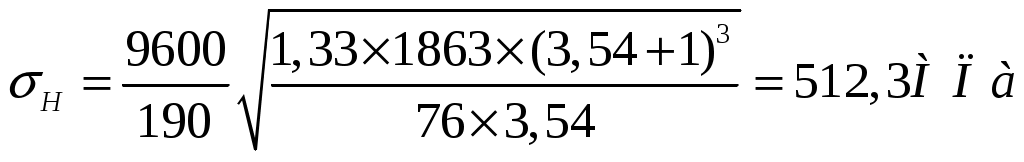 2.2.9 Силы в зацеплении. Окружная: Радиальная: Окружная: Радиальная: 2.2.10 Проверка зубьев колес по напряжения изгиба. напряжений, [ 1,стр 24, табл. 2.10 ] напряжений. [ 1,стр 24, табл. 2.10 ] 2.3 Расчет открытой конической передачи 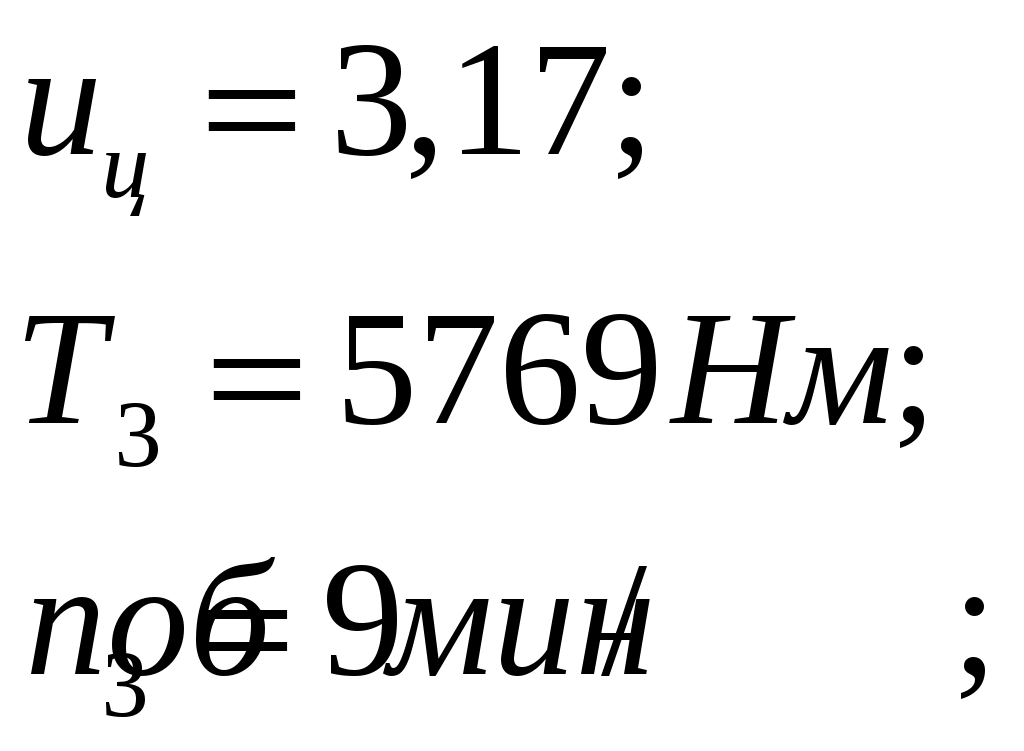 Колесо: материал – сталь 45, термообработка – улучшение; Шестерня: материал – сталь 45, термообработка – улучшение; Рассчитаем допускаемые контактные напряжения: 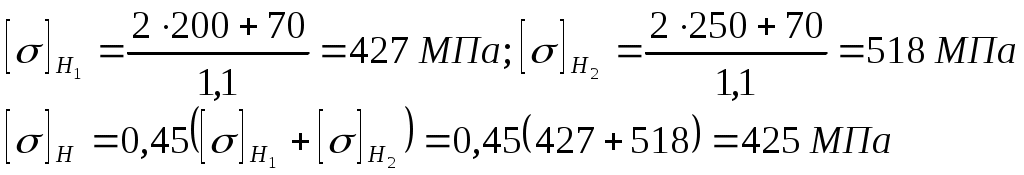 2.3.1 Предварительное значение диаметра внешней делительной окружности шестерни: 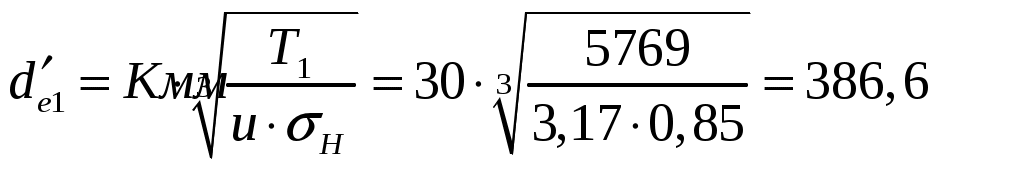 где Т1- вращающий момент на шестерне; u – передаточное число; σН =0,85 – для прямозубой конической передачи; К=30 – принимают в зависимости от твердости зубьев по таблице. Окружная скорость на среднем делительном диаметре: Где n1 – частота вращения шестерни. Принимаем прямозубые конические колеса 7-ой степени точности. Ресурс передачи при переменной нагрузке: Базовое число циклов: НВср – средняя твердость металла. NНО≤12·107 Коэффициент долговечности: Допускаемое контактное напряжение: SН=1,1 – для улучшенной стали. ZR=0.9…1 – коэффициент шероховатости. ZV=1…1,15 – коэффициент окружной скорости. Уточняем предварительно найденное значение диаметра внешней делительной окружности: 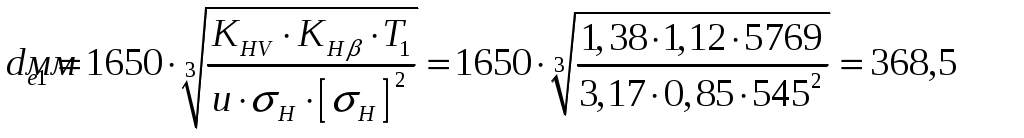 KHV=1,38 – коэффициент внутренней динамической нагрузки, KHβ=1,12 – коэффициент неравномерности распределения нагрузки, KHβ= KоHβ – для конических колес с прямыми зубьями, выбираемый по таблице, в зависимости от ψbd. 2.3.2 Угол делительного конуса шестерни: Внешнее конусное расстояние: Ширина зубчатого венца: 2.3.4 Внешний торцовой модуль передачи: 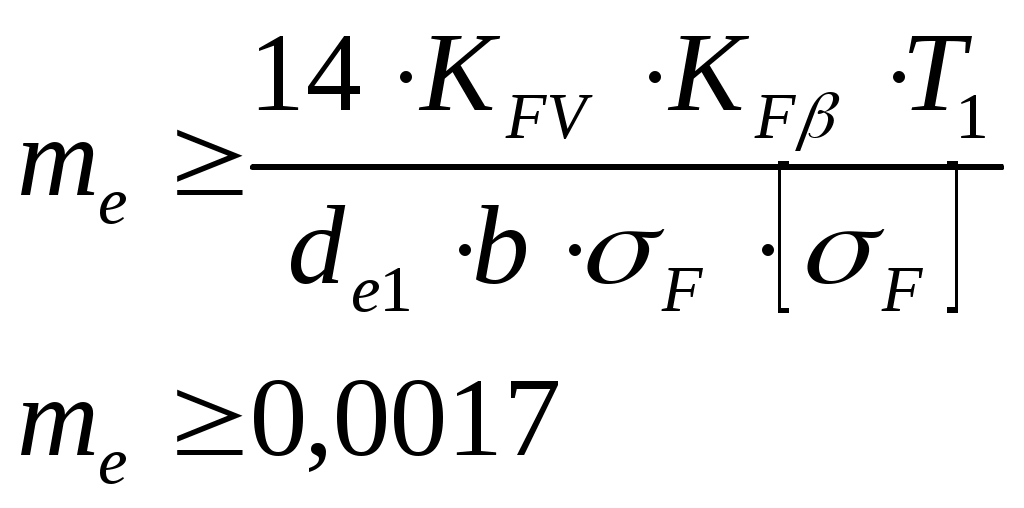 КFV=1,77 – коэффициент динамической нагрузки. Неравномерность распределения напряжений: SF=1,7 – коэффициент запаса прочности для улучшенных зубчатых колес. 2.3.5 Предварительное число зубьев шестерни определяют по графику: для При H1 и H2 ≤ 350 HB: Число зубьев колеса: Внешний окружной модуль передачи: 2.3.6 Фактическое передаточное число: 2.3.7 Окончательное значение размеров колес: Углы делительных конусов шестерни и колеса: 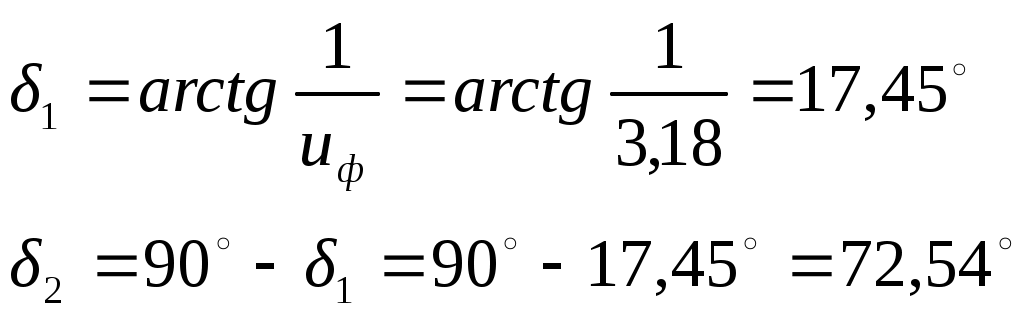 Делительные диаметры колес: Внешние диаметры колес: Коэффициент смещения шестерни: u=3,17 Коэффициент смещения для колеса: 2.3.8 Силы в зацеплении: Окружная сила на среднем диаметре шестерни: Осевая сила на шестерне: Радиальная сила на шестерне: Осевая сила на шестерне: Радиальная сила на шестерне: 2.3.9. Проверка зубьев колёс по контактным напряжениям: 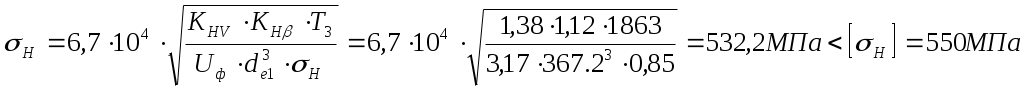 Проверка зубьев колёс на усталостный изгиб: Напряжение изгиба в зубьях колеса: 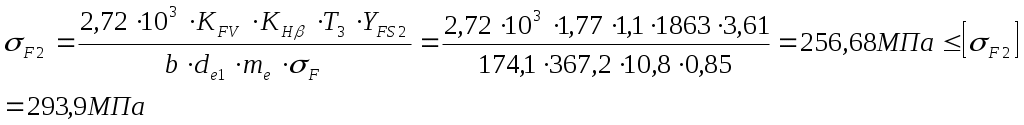 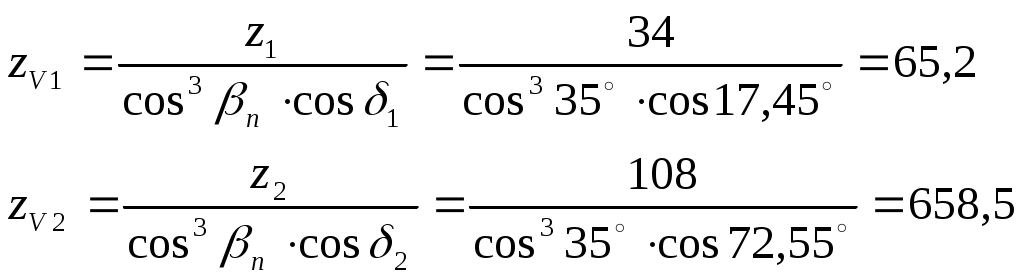 2.3.10 Проверочный расчет на прочность зубьев при действии пиковой нагрузки: Проверка зубьев на контактную прочность: Проверка зубьев на прочность по напряжениям изгиба: 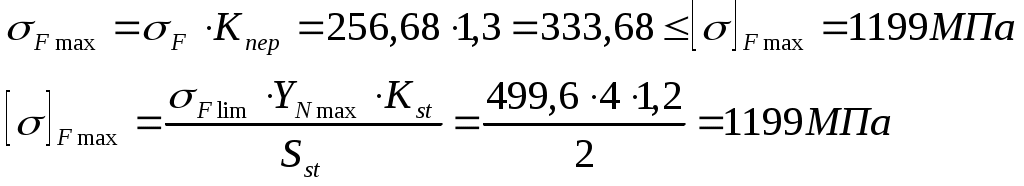 3. РасчЁт валов 3.1. Ориентировочный расчёт валов. 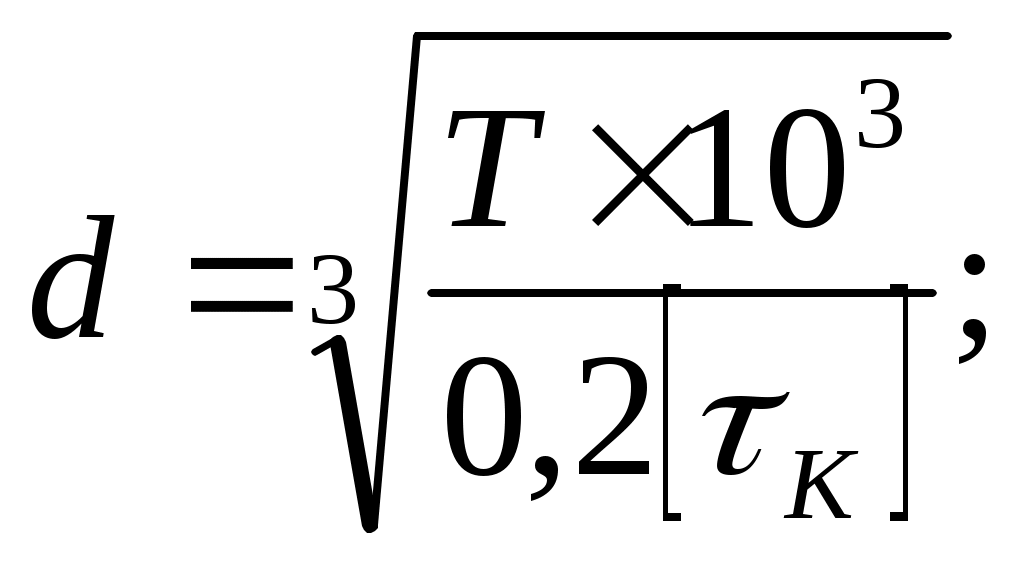 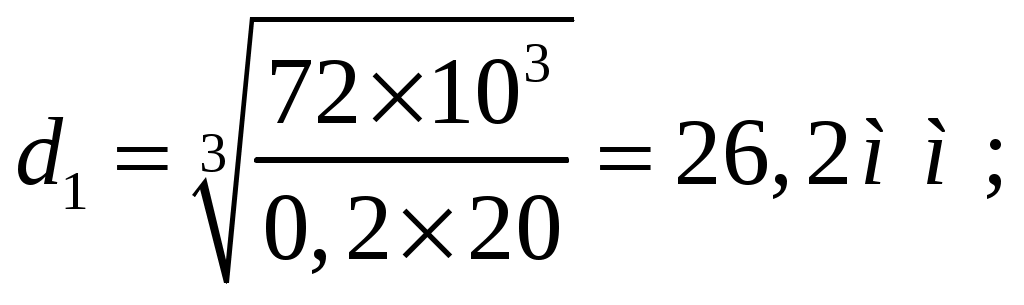 мм; мм; 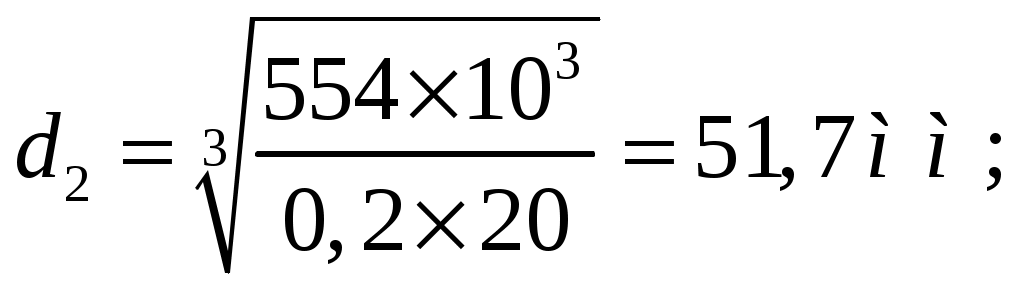 мм; мм;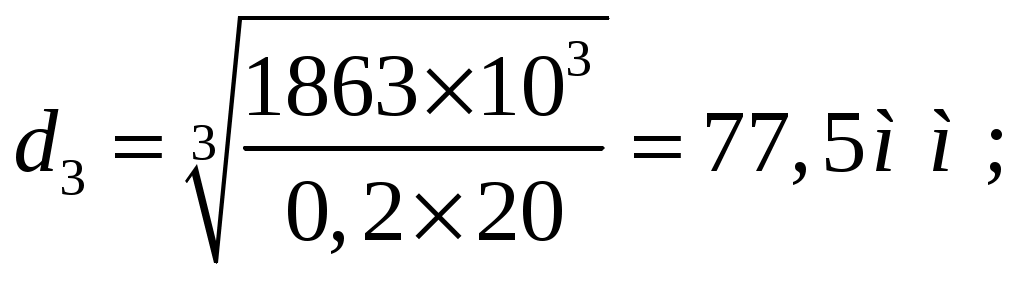 м м 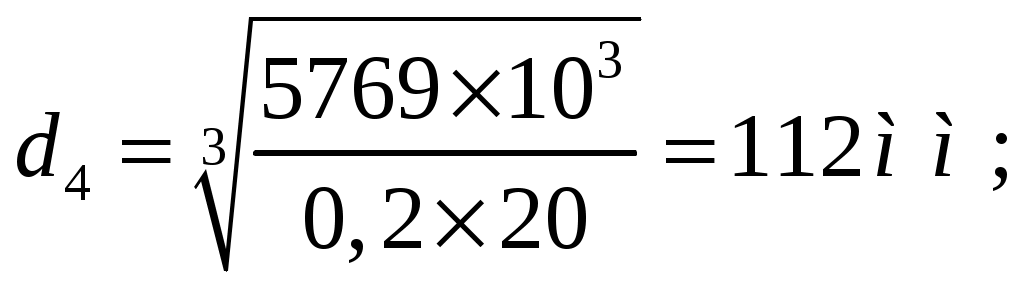 мм. мм.Окончательные значения диаметров валов: d1 = 30мм; d2=55мм; d3=80мм; d4 =120мм. 3.2. Тихоходный вал. d3=80мм. 3.2.1. Расчёт на статическую прочность. Расчёт проводим в следующей последовательности: по чертежу вала составляем расчётную схему, на которые наносят все внешние силы, нагружающие вал, приводя плоскости их действия к двум взаимно перпендикулярным плоскостям. Затем определяем реакции опор в горизонтальной и вертикальной плоскостях. В этих же плоскостях строим эпюры изгибающих моментов Исходные данные: Ϝt = 12588Н; Ϝr=4528Н; а =50мм; b=80мм. Горизонтальная плоскость: Проверка: Вертикальная плоскость: Проверка: 1 2 |
