Статистически значимые различия. испытуемых
 Скачать 42.35 Kb. Скачать 42.35 Kb.
|
|
Задание 3. Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?
Справочный материал Данное задание основано на теории дисперсионного анализа. В общем случае, задачей дисперсионного анализа является выявление тех факторов, которые оказывают существенное влияние на результат эксперимента. Дисперсионный анализ может применяться для сравнения средних нескольких выборок, если число выборок больше двух. Для этой цели служит однофакторный дисперсионный анализ. В целях решения поставленных задач принимается следующее. Если дисперсии полученных значений параметра оптимизации в случае влияния факторов отличаются от дисперсий результатов в случае отсутствия влияния факторов, то такой фактор признается значимым. Как видно из формулировки задачи, здесь используются методы проверки статистических гипотез, а именно – задача проверки двух эмпирических дисперсий. Следовательно, дисперсионный анализ базируется на проверке дисперсий по критерию Фишера. В данном задании необходимо проверить являются ли статистически значимыми различия между временем решения первых трёх заданий теста каждым из шести дошкольников. Нулевой (основной) называют выдвинутую гипотезу Hо. Сущность е сводится к предположению, что разница между сравниваемыми параметрами равна нулю (отсюда и название гипотезы – нулевая) и что наблюдаемые различия имеют случайный характер. Конкурирующей (альтернативной) называют гипотезу H1, которая противоречит нулевой. Решение: Методом дисперсионного анализа при уровне значимости α = 0,05 проверим нулевую гипотезу (Hо) о существовании статистически значимых различий между временем решения первых трёх заданий теста у шести дошкольников. Рассмотрим таблицу условия задания, в которой найдем среднее время решения каждого из трех заданий теста
Находим общую среднюю: 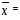 15,86667 15,86667Для того, чтобы учесть значимость временных различий каждого теста, общая выборочная дисперсия разбивается на две части, первая из которых называется факторной 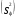 , а вторая – остаточной , а вторая – остаточной 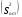 Рассчитаем общую сумму квадратов отклонений вариант от общей средней по формуле 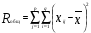 или или 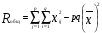 , где р – число измерений времени решений заданий теста, q – количество испытуемых. Для этого составим таблицу квадратов вариант , где р – число измерений времени решений заданий теста, q – количество испытуемых. Для этого составим таблицу квадратов вариант
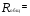 4356 4356Рассчитаем факторную сумму квадратов отклонений групповых средних от общей средней, которая и характеризует значимость данного фактора, т.е. различия между временем решения первых трёх заданий теста, по следующей формуле 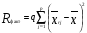 или или 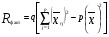 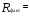 5*(219,04+ 60,84+ 625–3*251,7511) = 748,1333 5*(219,04+ 60,84+ 625–3*251,7511) = 748,1333Остаточная сумма квадратов отклонений получается как разность 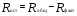 = 4356 – 748,1333 = 3607,867 = 4356 – 748,1333 = 3607,867Определяем факторную и остаточную дисперсии 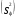 = = 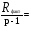 374,0667 374,0667 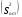 = = 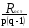 = =  300,6556 300,6556Находим  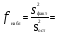 1,547959 1,547959Для уровня значимости α = 0,05 и чисел степеней свободы 2 и 12 находим 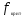 из таблицы распределения Фишера – Снедекора (смотри приложение основной литературы). из таблицы распределения Фишера – Снедекора (смотри приложение основной литературы).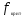 (0,05; 2; 15) = 3,885 (0,05; 2; 15) = 3,885В связи с тем, что 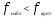 , нулевую гипотезу (Hо) о существовании статистически значимых различий между временем решения первых трёх заданий теста отвергаем и делаем вывод, т.е. принимаем альтернативную гипотезу (H1), что различия между временем решения первых трех заданий теста у пяти дошкольников статистически незначимы. , нулевую гипотезу (Hо) о существовании статистически значимых различий между временем решения первых трёх заданий теста отвергаем и делаем вывод, т.е. принимаем альтернативную гипотезу (H1), что различия между временем решения первых трех заданий теста у пяти дошкольников статистически незначимы.Ответ: При предъявлении теста пяти дошкольникам фиксируемое время решения каждого задания не является статистически значимым между временем решения первых трёх заданий теста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
