Математическое моделирование. Документ Microsoft Word. исследование и оптимизация свойств локальных информационных систем
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
|
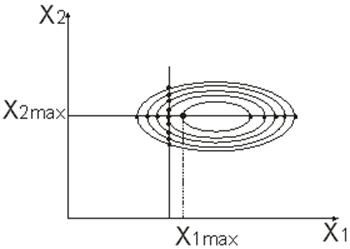
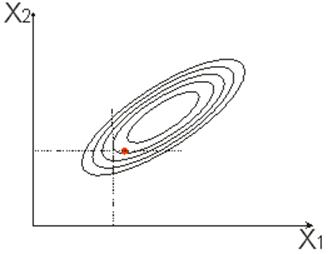
Модель объекта представляет собой аналитическую зависимость отклика от факторов. Чаще всего эта зависимость неизвестна, известными являются факторы xi и выходные величины отклика yi. Часто встречается задача исследования одной выходной величины у как функции нескольких факторов: yj = Fj (x1, x2, ... ,xn) Вид этой зависимости определяется из физической сущности, а численные значения коэффициентов вычисляются в соответствии с результатами эксперимента. Поэтому модель называют также эмпирической. Модель объекта может быть построена и на основе теоретически описания происходящих процессов. В этом случае модель называется теоретической. Одним из основных является требование простоты модели. При планировании эксперимента предполагается, что этому требованию отвечают алгебраические полиномы вида: Y=В0 + B1Х1 + … + BnХn + В12Х1Х2 + … Вnn-1ХnХn-1 + В11Х12 + … + ВnnXn2 +…. Разложение функции в степенной ряд возможно в том случае, если сама функция является непрерывной и гладкой. На практике обычно ограничиваются числом членов степенного ряда и аппроксимируют функцию полиномом некоторой степени. Функция отклика может быть выражена через кодированные факторы Y=f(x1,…, хn) и записана в полиномиальном виде Y=b0 + b1x1 + b2x2 … + bnxn + b12x1x2 + … bnn-1xnxn-1 + b11x12 + … + bnnxn2 +… Очевидно, что Bi≠bi, но Y=F(X1,…, Xi,…, Xn) = f(x1,…, xi,…, хn) Для полинома, записанного в кодированных факторах, степень влияния факторов или их сочетаний на функцию отклика определяется величиной их коэффициента bi. При определении общего числа членов степенного ряда количество парных сочетаний для n факторов в полиноме, тройных сочетаний, i-ых сочетаний при n>i находится по соотношению 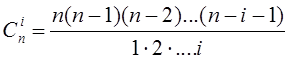 Например, для набора четырех чисел (n=4) - 1, 2, 3, 4 число тройных сочетаний составляет 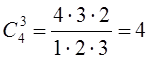 (123, 134, 124, 234) (123, 134, 124, 234)Если считать, что существует фактор х0 всегда равный 1, то 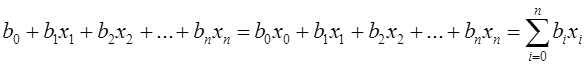 Если дополнительно все двойные, тройные и т.д. сочетания факторов, а также квадраты факторов и все соответствующие им коэффициенты для i=n+1,…m, обозначить через хi и bi, то степенной ряд можно записать в виде 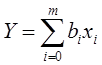 Здесь m+1 общее число рассматриваемых членов степенного ряда. Для линейного полинома с учетом всех возможных сочетаний факторов Полный квадратичный полином будет иметь вид:  где х0=1, х3=х1х2, х4=х12, х5=х22, b3=b12, b4=b11, b5=b22. При использовании методов планирования эксперимента для решения задачи построения математической модели объекта необходимо найти ответы на такие вопросы: · Какие сочетания факторов и сколько таких сочетаний необходимо взять для определения функции отклика? · Как найти коэффициенты В0, В1, … , Bm? · Как оценить точность представления функции отклика? · Как использовать полученное представление для поиска оптимальных значений Y? Математический аппарат планирования экспериментов позволяет проводить активный эксперимент и получать только необходимую информацию отдельно о каждом факторе или сочетании факторов. В частности, коэффициенты регрессии, которые являются основными характеристиками каждого фактора, определяются независимо друг от друга. Управляемость процесса получения информации заключается в том, что в процессе исследований ставятся эксперименты не по всем возможным сочетаниям факторов, а только по сочетаниям (значениям факторов в каждом эксперименте), которые обеспечат получение нужной информации. Это позволяет: 1) резко сократить количество опытов и облегчает обработку и анализ полученных результатов; 2) целенаправленно проводить исследования, четко обосновывая условия и количество экспериментов. Если высказывается гипотеза о линейной зависимости исследуемого процесса, то минимальное значение числа уровней факторов в экспериментах равно двум (-1 и +1), так как прямую линию можно построить по двум точкам. При количестве факторов равном n, количество экспериментов N будет равно . План, построенный таким образом, получил название полного факторного эксперимента (ПФЭ). При многофакторном эксперименте, особенно когда число факторов больше шести, число опытов планов ПФЭ становится слишком большим. Если нам не требуется определение всех коэффициентов неполного квадратичного полинома, то переходят к дробному факторному эксперименту (ДФЭ). Они представляют собой части полного факторного эксперимента (половину, четверть и т.д.) и называются дробными репликами ПФЭ, в которых количество опытов N уменьшается до значения . Вопрос 4. Поиск оптимальных значений. Часто возникающей на практике задачей является задача поиска значений параметров системы, обеспечивающих достижение оптимального значения показателя качества исследуемого объекта при известных ограничениях на значения параметров. Полный перебор всех допустимых сочетаний значений параметров системы с целью поиска оптимального варианта нерационален с точки зрения затрат необходимых ресурсов. Например, имея всего три фактора с пятью уровнями, потребуется провести Для нахождения оптимума может быть использован подход, называемый классическим, или методом Гаусса-Зейделя, который можно пояснить с помощью графического представления зависимости функции отклика одновременно от двух факторов в виде «контурной карты» (рис. 58Рис.):
|