Математическое моделирование. Документ Microsoft Word. исследование и оптимизация свойств локальных информационных систем
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
|
Тема 7. Модели на основе метода статистических испытаний Цели изучения темы: · изучить сущность моделирования на основе метода статистических испытаний. Задачи изучения темы: · изучить схему и границы применимости метода статистических испытаний; · изучить основные принципы компьютерной имитации случайных величин; · изучить способы имитации случайных событий. Успешно изучив тему, Вы: получите представление о: · когда применяется и как практически реализуется модель на основе метода статистических испытаний; · достоинства и недостатки метода статистических испытаний; будете знать: · как практически создаются и реализуются программные модели на основе метода статистических испытаний. Вопросы темы: 1. Метод статистических испытаний. 2. Случайные и псевдослучайные числа. 3. Имитация случайных событий. 4. Пример применения метода Монте-Карло. Вопрос 1. Метод статистических испытаний. Аналитические модели, рассмотренные ранее, могут с успехом применяться на этапе системного анализа и для решения ряда задач этапа проектирования, когда требования к точности результата не являются слишком строгими. Такими задачами могут быть задачи выбора конфигурации или модели сервера, где требуется определить только класс выбираемого устройства или подсистемы. Однако в ряде практических ситуаций применение аналитических моделей приводит к большой потере точности получаемого результата из-за того, что модели строятся на слишком приблизительном описании реальных процессов. В этих случаях можно использовать подход на основе имитационного моделирования процессов, который позволяет практически с любой степенью точности описать исследуемые процессы и отличается универсальностью применения. Рассмотрение имитационных моделей начнем с метода статистических испытаний. Статистическое моделирование является разновидностью имитационного моделирования и состоит в обработке данных о системе (модели) с целью получения статистических характеристик системы. Чаще всего оно применяется как способ исследования процессов поведения систем в условиях, когда внутренние взаимодействия в системах неизвестны, и построение аналитической модели явления затруднено или вовсе неосуществимо. Метод может применяться и на этапе системного анализа информационных систем, но основными для его применения являются задачи исследования операций, массового обслуживания и многие другие, связанные со случайными процессами. Эти задачи возникают в основном на этапах системного проектирования и разработки. Смысл метода Монте-Карло состоит в том, что исследуемый процесс моделируется путем многократных повторений его случайных реализаций (рис. 20). 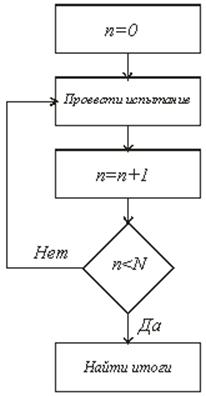 Рис. 20. Блок-схема метода Монте-Карло Единичные реализации называются статистическими испытаниями, в силу чего метод называется также методом статистических испытаний. Пусть, например, нам требуется найти значение числа π. Изобразим на декартовой плоскости две фигуры – квадрат и сектор круга, как это показано рис. 21: 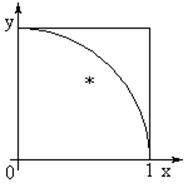 Рис. 21. Нахождение числа π методом Монте-Карло Предположим, что мы имеем генератор случайных чисел в диапазоне от [0;1], которые будем считать координатами x и y точки декартовой плоскости. Точка будет принадлежать области круга, если выполняется условие Тогда после многократно проведенных испытаний значение числа π можно приближенно оценить по формуле 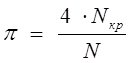 где - число попаданийточки в область квадрата (т.е., общее число реализаций). Метод применяется в тех случаях, когда построение аналитической модели явления затруднено или вовсе неосуществимо, например, при решении сложных задач теории массового обслуживания и ряда других задач исследования операций, связанных с изучением случайных процессов. В зависимости от особенностей решаемых задач метод Монте-Карло имеет ряд разновидностей и модификаций, которые повышают как точность результата, так и вычислительную эффективность процедуры. Недостатком метода Монте-Карло являются большие затраты машинного времени, требуемые для достижения большей статистической точности: известно, что для уменьшения дисперсии результата в k раз, число испытаний необходимо увеличить в раз. Вопрос 2. Случайные и псевдослучайные числа. В основе вычислений по методу статистических испытаний лежит случайный выбор чисел из заданного вероятностного распределения. Чисто случайныепоследовательности выдают аппаратурные средства, например, базирующиеся на усилении и обработке теплового шума электронных схем. При практических вычислениях эти числа берут из таблиц или получают путем выполнения некоторых операций, результатами которых являются псевдослучайные числа с теми же свойствами, что и числа, получаемые путем случайной выборки. Имеется большое число вычислительных алгоритмов, которые позволяют получить длинные последовательности псевдослучайных чисел (последовательности (имеющие цикл повтора, но очень длительный). Реализующие эти алгоритмы программы называются генераторами случайных чисел. Имеется большое число вычислительных алгоритмов, которые позволяют получить длинные последовательности псевдослучайных чисел. Один из наиболее простых и эффективных вычислительных методов получения последовательности равномерно распределенных на интервале [0,1] случайных чисел, включающий только одну операцию умножения, разработан Лехмером и известен как метод линейного конгруента. Алгоритм имеет четыре параметра: m модуль (основание системы), m > 0 a множитель, 0 ≤ a < m c приращение, 0 ≤ с < m начальное значение, Последовательность случайных чисел {Xn} получается с помощью следующего итерационного равенства: Если m, а и с - целые, то создается последовательность целых чисел в диапазоне Выбор значений а, с и m является критичным для разработки хорошего генератора случайных чисел. Очевидно, что m должно быть очень большим, чтобы была возможность создать множество случайных чисел. Считается, что m должно быть приблизительно равно максимальному положительному целому числу для данного компьютера. Для 32-х разрядных ЭВМ обычно значение m близко или равно 231. Значения а, с и m должны быть выбраны таким образом, чтобы эти три критерия выполнялись. В соответствии с первым критерием можно показать, что если m является простым и с = 0, то при определенном значении а период, создаваемый функцией, будет равен m-1. Для 32-битной арифметики соответствующее простое значение m = 231 - 1. Таким образом, функция создания псевдослучайных чисел имеет вид: Только небольшое число значений а удовлетворяет всем трем критериям. Одно из таких значений а = 75 = 16807, которое использовалось в семействе компьютеров IBM 360. Для задания базового значения в программе использовано битовое содержимое таймера компьютера, что обеспечивает случайных характер выбора начальной точки последовательности чисел. Это удобно для проведения экспериментов на модели, но создает сложности в процессе ее отладки, так как не дает возможность обеспечить воспроизводимость запусков. С целью обойти эту проблему следует задавать в качестве начального значения конкретную величину, одну и ту же для всех отладочных тестов. Программа на языке С++ может быть реализована в виде (начальное значение bx получается путем считывания с компьютерного таймера): double rundum(void) { long static bx = (long)time(NULL); unsigned long m =2<<31 - 1; if (bx % 2 == 0) bx++; bx = (16807 * bx) % m ; return((long double) bx / (long double)m); } В случае, если начальное значение bx четное, оно заменяется на ближайшее большее нечетное для улучшения свойств получаемой последовательности. Для получения случайной величины y, равномерно распределенной на интервале (a,b), можно воспользоваться выражением где x - случайная величина, равномерно распределенная на интервале (0,1). Программа на языке С++: double unifrm (float m , float s) { return ( m-s + 2*s*rundum() ); } Вопрос 3. Имитация случайных событий. Во многих программах, которые реализуют метод Монте-Карло необходимо уметь имитировать наступление некоторых событий, например, нахождение некоторого устройство в рабочем или нерабочем состоянии для решения задачи оценивания надежности системы, которая включает это устройство. Для этого используется следующий метод. Пусть некоторое событие А происходит с вероятностью РА. Требуется воспроизвести факт наступления события А. Поставим в соответствие событию А событие В, состоящее в том, что х ≤ РА, где х случайное число с равномерным на интервале (0,1) законом распределения. Вычислим вероятность события В: 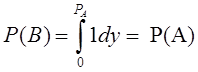 Таким образом, события А и В являются равновероятными. Отсюда вытекает процедура имитации факта появления события А. Она сводится к проверке неравенства х ≤ РА, и алгоритм заключается в следующем: 1) Генерируется случайное число х; 2) Проверяется выполнение неравенства х ≤ Р(А); 3) Если неравенство выполняется, считается, что событие А произошло, если нет – не произошло. Программа на языке С++: int event(double P) { if (rundum()<= P) return (1); else return (0); } Функция event возвращает значение 1 в случае наступления в очередном испытании события с вероятностью Р, и 0 в противном случае. Вопрос 4. Пример применения метода Монте-Карло. Рассмотрим теперь, как практически применяется метод Монте-Карло к решению задачи оценивания надежности простой структуры, изображенной на рис 22. 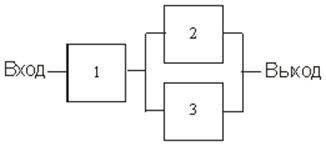 Рис. 22. Пример для метода Монте-Карло Для каждого из блоков 1, 2, 3 заданы вероятности их нахождения в работоспособном состоянии. Считая, что вся схема находится в работоспособном состоянии в случае, если между входом и выходом существует хотя бы одна цепочка работоспособных блоков, необходимо оценить вероятность ее нахождения в работоспособном состоянии. Решить эту задачу без особого труда можно с помощью теории вероятностей. Действительно, сначала заменим блоки 2 и 3 одним блоком с эквивалентной надежностью. Возможными исходами для этого фрагмента схемы будут: где означает работоспособность, а - неработоспособность блока с номером i. Полезными исходами являются первые три из перечисленных, вероятность наступления одного из которых находится как сумма вероятностей наступления каждого: Поскольку все перечисленные исходы составляют полную группу событий, то и Поскольку события а так как вероятность противоположного события находится как разность между 1 вероятностью самого события, то Вся схема будет работоспособна, если одновременно будут работоспособны блок 1 и «виртуальный» блок 23. Поскольку эти события можно считать независимыми, то вероятность одновременного наступления этих событий найдется как произведение вероятностей каждого из событий, т.е.: где Например, для значений вероятностей блоков 1, 2, 3 равных соответственно 0,95; 0,9; 0,85 расчет по формуле (1) (1) дает 0,93575. Решим теперь эту же задачу, воспользовавшись схемой метода Монте-Карло. Целью каждого испытания будет проверка работоспособности схемы. Смоделировать исход каждого испытания в компьютерной модели можно в два этапа: сначала сымитировать работоспособность или поломку каждого из трех блоков, а затем определить конечный результат. Первый этап реализуется как имитация наступления события с заданной вероятностью, процедура которой уже была рассмотрена. Второй этап состоит в проверке истинности логического условия, которое в данном случае выглядит как: Программная модель на языке С++ имеет вид:
Значения параметров моделирования задаются в разделе с заголовком (строкой комментария) «Параметры запуска модели». Здесь задаются число повторений экспериментов N и вероятности работоспособности блоков P1, P2, P3. Значения равномерно распределенного в промежутке [0,1] случайного числа получаются с помощью функции rundum, построенной на основе уже рассмотренного в данной теме конгруентного алгоритма. Функция event позволяет имитировать наступление события с заданной вероятностью (также рассмотрена ранее). Оценка вероятности работоспособного состояния находится как отношение счетчика числа успешных испытаний Результаты выводятся в файл, обозначаемый переменной reportfile. Если провести запуски программы с числом испытаний равным 100, 1000 и 1000000, то результатами будут значения надежности 0,93; 0,947 и 0,936093. Выводы: 1. Аналитические модели во многих практических ситуациях не могут обеспечить требуемой точности результатов. Универсальным средством преодолеть эти трудности является методология имитационного моделирования, практически не имеющая ограничений в смысле возможных применений и точности получаемых с ее помощью оценок показателей системы. 2. В случае, когда задача нахождения значений показателей изучаемого процесса не требует воспроизведения процесса в динамике и в модель не включаются описания внутренних механизмов протекания процессов, весьма полезным является применение метода статистических испытаний. Его схема отличается простотой, реализация на компьютере не требует специальных средств, однако для сложных задач сопряжена с большим расходованием времени на проведение машинных экспериментов. 3. Реализация машинных экспериментов в условиях действия случайных факторов требует использования генераторов случайных чисел и имитаторов случайных событий. Для построения генераторов и имитаторов разработаны специальные алгоритмы, обеспечивающие получение с помощью построенных на их основе компьютерных программ необходимых результатов с требуемыми характеристиками. Вопросы для самопроверки: 1. Что такое компьютерное моделирование, и в каких случаях целесообразно его применять? 2. В чем заключается идея метода статистических испытаний? 3. Когда следует применять метод статистических испытаний? 4. Из каких шагов состоит вычислительная процедура метода статистических испытаний? 5. Поясните применение метода статистических испытаний на примере определения надежности схемы. 6. Чем достигается статистическая точность метода статистических испытаний? 7. Как зависит точность результата, полученного на основе метода статистических испытаний, от числа проведенных испытаний? 8. В чем заключаются основные достоинства и недостатки метода статистических испытаний? Литература по теме: 1. Емельянов А.А., Власова Е.А., Дума Р.В., Емельянова Н.З. Компьютерная имитация экономических процессов: Учебник / Под ред. А.А. Емельянова. – М.: Маркет ДС, 2010. – 464 с. | ||||||||||||||||||||||||||||||||||||||||||||||
