Математическое моделирование. Документ Microsoft Word. исследование и оптимизация свойств локальных информационных систем

• Название: исследование и оптимизация свойств локальных информационных систем
• Анкор: Математическое моделирование
• Дата: 23.06.2021
• Размер: 1.67 Mb.
• Имя файла: Документ Microsoft Word.docx
• Тип: Исследование; #220711
• страница: 5 из 15

Тема5. Непрерывные марковские процессы

 

Цели изучения темы:

·     познакомиться с математическим аппаратом аналитического моделирования непрерывных марковских процессов;

 

Задачи изучения темы:

·     изучить математический аппарат описания марковских процессов;

·     научиться находить характеристики процесса с помощью уравнений Колмогорова.

 

Успешно изучив тему, Вы:

получите представление о:

·     как построить математическую модель непрерывного марковского процесса;

·     что такое стационарный режим и предельные вероятности;

·     как найти вероятности нахождения марковского процесса в своих состояниях;

·     что такое процесс гибели и размножения и как он используется для моделирования практических задач.

 

будете знать:

·     как описать непрерывно протекающие процессы с помощью графа состояний и переходов;

·     что такое интенсивности перехода процесса;

·     как составить уравнения Колмогорова по графу состояний и переходов;

·     как применить аппарат теории марковских процессов к практическим задачам построения систем.

 

Вопросы темы:

1.  Описание непрерывных цепей Маркова.

2.  Уравнения Колмогорова.

3.  Процессы гибели и размножения.

 

Вопрос 1. Описание непрерывных цепей Маркова.

 

Рассмотрим пример. Пусть имеем системуS, включающую один компьютер, который может находиться в одном из пяти возможных состояний:

S₁ — исправен, работает;

S₂ — неисправен, ожидает осмотра;

S₃ — осматривается;

S₄ — ремонтируется;

S₅ — списан.

 

ГСП системы показан на рис. 10.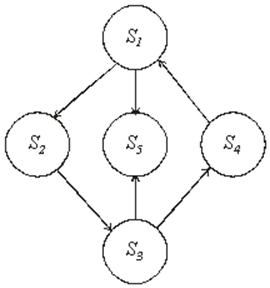

 



 

Рис. 10. Граф состояний и переходов процесса поломок и восстановлений

 

В примере на рис. 10 выход из строя (отказ) компьютера и окончание его ремонта (восстановление) могут произойти в заранее неизвестный момент. Для описания таких процессов может быть применена схема марковского случайного процесса с дискретными состояниями и непрерывным временем. Процессы такого типа известны как непрерывные цепи Маркова. Непрерывной цепью Маркова (марковским процессом) называется процесс, для которого при  выполняется:

 



 

Здесь рассматривается ряд дискретных состояний: S₁, S₂, S₃, ..., S_n, однако переход системы S из состояния в состояние может происходить в произвольный момент времени.

Обозначим через p_i(t) вероятность того, что в момент t система Sбудет находиться в состоянии S_i(i= 1, ... , n). Очевидно, для любого момента t сумма вероятностей состояний равна единице: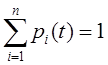

 

            (1)

 

Так как события, состоящие в том, что в момент t система находится в состояниях S₁, S₂ , ..., S_n , несовместны.

Необходимо определить для любого t вероятности состояний:

 

             (2)

 

Для того чтобы найти эти вероятности, необходимо знать характеристики процесса. Поскольку вероятность перехода системы из состояния в состояние точно в момент t будет равна нулю (так же как вероятность любого отдельного значения непрерывной случайной величины), то в качестве характеристик процесса рассматриваются плотности вероятностей, или интенсивности перехода λ_ij из состояния S_iв состояние S_j.

Пусть система S в момент t находится в состоянии S_r. Рассмотрим элементарный промежуток времени Δt, примыкающий к моменту t. Назовем плотностью вероятности переходаλ_ij из состояния i в состояние j предел отношения вероятности перехода системы за время Δt из состояния S_i в состояние S_j к длине промежутка Δt: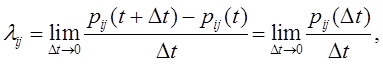

 

               (3)

 

где

Pij(Δt) — вероятность того, что система, находившаяся в момент t в состоянии S_i за время Δt перейдет из него в состояние S_j (плотность вероятностей перехода определяется только для j≠i).

 

Из (3) следует, что при малом Δt вероятность перехода (с точностью до бесконечно малых высших порядков) равна:

 

Pij(Δt)=λij Δt

 

Если все плотности вероятностей перехода λ_ij не зависят от t (от того, в какой момент начинается элементарный участок Δt)

 

,

 

то марковский процесс называется однородным, в противном случае - неоднородным.

Предположим, что известны плотности вероятностей перехода λ_ijдля всех пар состояний S_i,S_j. ГСП системы с проставленными у стрелок плотностями вероятностей перехода называется размеченным графом состояний (рис. 11), на основании которого можно определить вероятности состояний р_i(t) как функции времени (2) .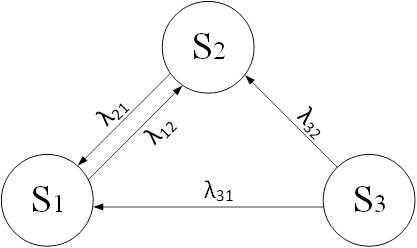

 



 

Рис. 11. Пример размеченного графа состояний и переходов

 

Вопрос 2. Уравнения Колмогорова.

 

Если протекающий в системе случайный процесс является марковским процессом с непрерывным временем, то для вероятностей   можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова. Покажем, как получаются эти уравнения на примере ГСП рис 11.

Рассмотрим вначале вершину графа  . Вероятность  того, что система в момент времени (t + Δt) окажется в состоянии  , определяется на основе рассмотрения трех возможностей попасть в это состояние:

1)      Система в момент времени t с вероятностью  находиласьв состояниии за малоевремя Δt не перешла в состояние . Из состояниясистема может быть выведенапотоком интенсивностью . Вероятность выхода системы из состоянияза время Δt с точностью до величин более высокого порядка малости по Δt равна  , а вероятность сохранения состояния  будет равна  .

При этом вероятность того, что система останется в состоянии, согласно теореме об умножении вероятностей будет равна .

 

2)      Система в момент времени t находилась в состояниии за время Δt под воздействием потока перешла в состояние с вероятностью  . Вероятность того, что система будет находиться в состоянии  ,равна .

3)      Система в момент времени t находилась в состояниии за время Δt под воздействиемпотокаперешла в состояниес цвероятностью  . Вероятность того, чтосистема будет находиться в состоянии,равна .

 

По теореме сложения вероятностей получим:

 



 



 



 

и, переходя к пределу Δt → 0,

 



 

Аналогично, рассматривая вершины графаи  , получим уравнения

 



 



 

К этим уравнениям необходимо добавить нормировочное условие, которое в данном случае имеет вид

 



 

Решение этой системы уравнений в зависимости от времени можно найти либо аналитически, либо численно с учетом начальных условий.

На основе рассмотренного примера можно сформулировать общее правило составления уравнений Колмогорова:

В левой части каждого уравнения стоит производная вероятности какого-то (j-го) состояния. В правой части - сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков, минус суммарная интенсивность всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния.

Это правило составления дифференциальных уравнений для вероятностей состояний является универсальным и применимо к любому марковскому процессу с непрерывным временем; с его помощью можно без проведения специального рассмотрения условий задачи, записывать дифференциальные уравнения для вероятностей состояний непосредственно по размеченному графу состояний.

Весьма важным является вопрос о том, что будет происходить с системой при  , а именно, будут ли функции р(t), р₂(t), ... , р_n(t) стремиться к каким-то пределам. Эти пределы, если они существуют, называются предельными (или финальными) вероятностями состояний.

В самой системе S устанавливается некоторый предельный стационарный режим: система хоть и меняет случайным образом свои состояния, но вероятность каждого из них не зависит от времени и каждое из состояний осуществляется с некоторой постоянной вероятностью, которая представляет собой среднее относительное время пребывания системы в данном состоянии. Например, если у системы три возможных состояния:  ,   и  , причем их предельные вероятности равны 0,2; 0,3 и 0,5, то это означает, что после перехода к установившемуся режиму система в среднем 20% времени будет находиться в состоянии  , 30% — в состоянии   и 50% — всостоянии.

Доказано, что если число состояний системы S конечно и из каждого состояния можно перейти (за то или иное число шагов) в любое другое, то предельные вероятности состояний существуют и не зависят от начального состояния системы. В этом случае в процессе моделирования системы можно ограничиваться для нахождения ее параметров одной достаточно длинной реализацией процесса.

Вычислить все предельные вероятности можно, перейдя от системы дифференциальных уравнений к системе линейных алгебраических уравнений, дополнив ее нормировочным условием.

Найдем финальные вероятности pj системы уравненийдля ГСПна рис 11. Полагая dpi/dt = 0 (j=1,2, 3)получаем три алгебраических уравнения, которые являютсяоднородными. Поэтому одно из них можно отбросить. Отбросим,например, второе уравнение и вместо него запишем нормировочное условие. В результате система уравнений для финальных вероятностей примет вид:

 



 

Из последнего уравнения следует, что

 

p3 = 0

 

Решая оставшиеся уравнения, получим

 

p1= 2/3,

 

p2 = 1/3

 

Т.е., вектор состояния системы в стационарном режиме равен

 



 

Как мы увидели, имея размеченный ГСП системы, можно сразу написать алгебраические уравнения для предельных вероятностей состояний. Таким образом, если две непрерывные цепи Маркова имеют одинаковые графы состояний и различаются только значениями интенсивностей λ_ij, отсутствует необходимость находить предельные вероятности состояний для каждого из графов в отдельности, достаточно составить и решить уравнения для одного из них, а затем подставить вместо λ_ijсоответствующие значения. Для многих часто встречающихся на практике форм графов линейные уравнения без особых затруднений решаются в алгебраическом виде.

Рассмотрим практический пример. Пусть имеется система, состоящая из двух серверов, которая обрабатывает поток поступающих к ней запросов (рис. 12, а).

 



 

Рис. 12. Система с двумя серверами

 

Средний интервал между поступлениями запросов  , производительность серверов неодинакова: среднее время обработки запроса первым сервером составляет  , второго –  ,  .

Если в момент поступления в систему очередной заявки:

·     первый сервер свободен, то заявка берется на обработку первым сервером;

·     первый сервер занят обслуживанием, а второй сервер свободен, то заявка берется на обработку вторым сервером;

·     оба сервера заняты обслуживанием, то заявка теряется.

 

В предположении экспоненциального характера распределения  ,  ,   требуется найти вероятность отказа в обслуживании запроса .

В силу экспоненциального характера распределения временных параметров процесс можно считать марковским. Поэтому решение задачи начинаем с построения ГСП процесса.

Исследуемый процесс может находиться в следующих состояниях:

 

S₀₀ – оба сервера свободны,

S₁₀ – первый сервер занят, второй свободен,

S₀₁ – первый сервер свободен, второй занят,

S₁₁ – оба сервера заняты.

 

Если обозначить

 - интенсивность потока запросов к системе;

 - интенсивность обработки запросов первым сервером;

 - интенсивность обработки запросов вторым сервером.

 

то размеченный ГСП будет иметь вид, показанный на рис. 12, б.

Соответствующие уравнения Колмогорова для установившегося режима:

 



 

Вероятность отказа в обработке запроса есть не что иное как вероятность  занятости обслуживанием обоих серверов. Оставив из имеющихся уравнений три и дополнив их условием нормировки:

 



 

решаем далее полученную систему линейных алгебраических уравнений (например, методом подстановки).

 

Вопрос 3. Процессы гибели и размножения.

 

Важной разновидностью непрерывных марковских цепей является процесс гибели и размножения. Происхождение термин берет в биологии, где такая схема описывает процессы изменения численности популяции, распространения эпидемий и т.п.

Марковская непрерывная цепь называется процессом гибели и размножения, если ее ГСП имеет вид, представленный на рис. 13.

 



 

Рис. 13. Процесс гибели и размножения

 

Граф на рисунке имеет вид цепочки, крайние звенья которой связаны переходами только с одним соседним звеном, а каждое внутреннее связано прямой и обратной связью с каждым из соседних. Величины   (интенсивности переходов системы из состояния в состояние слева направо) можно трактовать как интенсивности рождения, величины   (интенсивности переходов системы из состояния в состояние справа налево) - как интенсивности гибели.

Запишем алгебраические уравнения для вероятностей состояний в установившемся режиме. Для каждого состояния поток, втекающий в данное состояние, должен равняться потоку, вытекающему из данного состояния.

Для состояния  :

 



 

Для состояния  :

 



 

С учетом равенства для состояния S₁ равные друг другу члены справа и слева можно сократить, поэтому получаем:

 



 

Аналогично, для  :

 



 

Вообще для состояния k, k = 2,..n, имеем:

 



 

Таким образом, предельные вероятности состояний  , , ... ,  процесса размножения и гибели можно найти из уравнений:

 



 



 



 



 



 

которые нужно дополнить нормировочным условием: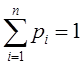

 



 

Последовательно выразим из каждого уравнения переменные через  .

Из первого уравнения выразим :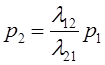

 



 

Из второго уравнения с учетом выражения для   выразим  :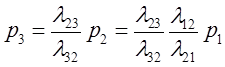

 



 

Вообще, для k , k = 2, ... n, имеем: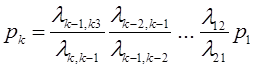

 



 

Подставив полученные выражения для  , , ... , в нормировочное условие и вынося  , получаем:

 



 

Остальные вероятности легко выражаются через  .

Как показано в ряде работ, для существования стационарного режима необходимо и достаточно необходимо и достаточно, чтобы  .

Рассмотрим простой практический пример. Пусть небольшой компьютерный класс состоит из трех одинаковых компьютеров,каждый из которых может выходить из строя с интенсивностью l=1 компьютер/сутки. Отказавший компьютер немедленно начинает восстанавливаться, на восстановление уходят в среднем также одни сутки, m=1 сутки -1. Требуется найти вероятности числа неисправных компьютеров.

Определим возможные состояния системы:

 - все три компьютера исправны;

 - один компьютер восстанавливается, два исправны;

 - два компьютера восстанавливаются, один исправен;

 - все три компьютера восстанавливаются.

 

Размеченный ГСП системы показан на рис. 14.

 



 

Рис. 14. Процесс поломок и восстановлений компьютерного класса

 

Из графа видно, что процесс, протекающий в системе, представляет собой процесс гибели и размножения. Значения интенсивностей переходов для состояния с номером k определяются так: интенсивность перехода в состояние с большим номером равна  , поскольку интенсивность поломок кратна числу исправных компьютеров  ; интенсивность перехода в состояние с меньшим номером равна , поскольку интенсивность восстановления кратна числу неисправных компьютеров  .

Используя выражения для вероятностей состояний процесса гибели и размножения, получаем: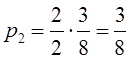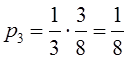

 



 



 



 



 

Выводы:

1.  В ряде практически важных случаев протекающие в системах процессы могут быть описаны как марковские процессы с дискретным множеством состояний и непрерывным временем. Это позволяет применить для их математического описания аппарат дифференциальных уравнений Колмогорова, с помощью которых можно получить числовые характеристики процессов.

2.  Особый интерес во многих прикладных задачах представляет стационарный режим, в который по истечении некоторого времени входит марковский процесс. Если такой режим существует, то предельные вероятности находятся путем решения системы алгебраических линейных уравнений, получаемых из уравнений Колмогорова дополненных нормировочным условием.

3.  Важным частным случаем марковских процессов с непрерывным временем являются процессы гибели и размножения. Их обобщенное решение, получаемое на основе уравнений Колмогорова, позволяет решать целый класс практических задач и строить модели многих систем, в частности, систем массового обслуживания, которые будут рассматриваться в следующей теме.

 

Вопросы для самопроверки:

1.      Дайте определение марковского процесса с непрерывным временем и дискретными состояниями?

2.      Как описывается марковского процесса с непрерывным временем и дискретными состояниями?

3.      Что такое интенсивность перехода?

4.      Что такое установившийся режим?

5.      Каким правилом можно пользоваться для записей уравнений Колмогорова?

6.      Что такое предельные вероятности марковского процесса?

7.      При каких условиях существуют предельные вероятности состояний марковского процесса?

8.      Каков физический смысл предельных вероятностей?

9.      Как найти предельные вероятности системы, имеющей стационарный режим?

10.  Что называется процессами гибели и размножения? Поясните на ГСП.

11.  Запишите выражения для предельных вероятностей процесса гибели и размножения.

12.  Приведите практические примеры процессов, описываемых как марковские процессы с непрерывным временем и дискретными состояниями.

 

Литература по теме:

1.  Емельянов А.А., Власова Е.А., Дума Р.В., Емельянова Н.З. Компьютерная имитация экономических процессов: Учебник / Под ред. А.А. Емельянова. – М.: Маркет ДС, 2010. – 464 с.

2.  Саати Т.Л. Элементы теории массового обслуживания и её приложения. – М.: Радио и связь, 1965. – 512 с.

3.  Климов Г.П. Теория массового обслуживания. – М.: Издательство МГУ, 2011. – 312 с.