Математическое моделирование. Документ Microsoft Word. исследование и оптимизация свойств локальных информационных систем
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
|
Тема 6. Модели систем массового обслуживания Цели изучения темы: · познакомиться с основными аналитическими моделями систем массового обслуживания. Задачи изучения темы: · научиться применять математический аппарат описания марковских процессов к построению моделей систем массового обслуживания; · познакомиться с основными показателями, используемыми в моделях систем массового обслуживания. Успешно изучив тему, Вы: получите представление о: · как строятся математические модели систем массового обслуживания на примере системы с отказами; · как применяются модели систем массового обслуживания; будете знать: · как характеризуется пропускная способность систем с отказами и как они рассчитываются; · какие показатели характеризуют очередь в системе с ожиданием и как они рассчитываются; · как применить модели к решению экономических и инженерных задач. Вопросы темы: 1. Система массового обслуживания. 2. Моделирование одноканальной СМО с отказами. 3. Оптимизация показателей многоканальной СМО с отказами. 4. Обслуживание с очередями. 5. Многоканальная СМО сограниченной очередью. Вопрос 1. Система массового обслуживания. Значительный интерес для практики представляют модели систем массового обслуживания(СМО), к которым сводятся множество задач анализа и проектирования информационных систем. Системы этого класса характеризуются наличием (рис. 15) потока запросов (заявок), поступающих на вход системы (входящим потоком), необязательной очереди ждущих обслуживания заявок, обслуживающим прибором, или каналом и потоком обслуженных заявок (выходящим потоком). 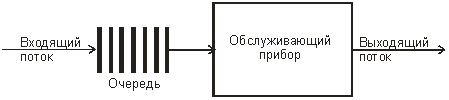 Рис. 15. Элементы СМО Поток заявок (другие названия: запросы, вызовы, требования и т.д.), исходящий из источника заявок, поступает на вход СМО в случайные моменты времени для обслуживания. Этот входной поток может представлять собой вызовы от абонентов, передаваемые сообщения и т.д. Обслуживание поступившей заявки продолжается некоторое случайное время, после чего канал освобождается и готов к принятию следующей заявки. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на входе СМО скапливается излишне большое число заявок (они либо образуют очередь, либо покидают СМО не обслуженными); в другие же периоды СМО будет работать с недогрузкой или простаивать. Для СМО в рамках теории массового обслуживания разработаны математические модели, которые широко применяются для количественного оценивания системных показателей. Многие модели основаны на уже рассмотренном ранее аппарате марковских процессов. Проиллюстрируем применение теории на нескольких моделях СМО. Вопрос 2. Моделирование одноканальной СМО с отказами. Примером одноканальной СМО с отказами, которая является простейшей из моделей, может служить телефонное справочное бюро. В случае незанятой линии происходит соединение с оператором, и абонент получает ответ на заданный вопрос, в противном случае соединение не устанавливается и звонок необходимо повторить. Считая интервалы между звонками и продолжительность разговора случайными величинами, распределенными по экспоненциальному закону, процесс в такой системе можно рассматривать как марковский. Обозначив через l интенсивность входящего потока, m - интенсивность обслуживания, можно построить размеченный ГСП (рис. 16Рис.) . 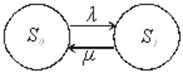 Рис. 16. ГСП одноканальной СМО с отказами Вероятности состояний системы (вероятность того, что в системе находится 0 заявок) и (вероятность того, что в системе находится 1 заявка) для стационарного режима определяются из выражений для вероятностей состояний процесса гибели и размножения, который был рассмотрен в предшествующей теме: 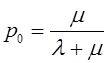 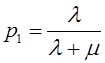 Из этих выражений можно определить показатели одноканальной СМО. В частности, вероятность отказа в обслуживании 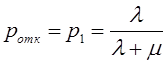 (1) (1)поскольку запрос получает отказ в случае, когда обслуживающий прибор занят, и относительную пропускную способность , которая представляет собой отношение среднего числа обслуженных заявок за единицу времени к среднему числу всех поступивших заявок за тоже время: 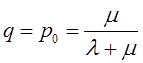 (2) (2)Поскольку есть вероятность того, что в момент t канал свободен, или вероятность того, что заявка, пришедшая в момент t, будет обслужена. Зная q легко найти абсолютную пропускная способность А, которая определяется как среднее число заявок, которое может обслужить СМО в единицу времени. Эти показатели связаны очевидным соотношением Вопрос 3. Оптимизация показателей многоканальной СМО с отказами. В многоканальной СМО имеется n каналов обслуживания, которые функционируют независимо друг от друга. Очередь отсутствует, т.е., заявки, заставшие все каналы занятыми обслуживанием, получают отказ, и уходят из системы. Входной поток заявок и поток обслуживания заявок являются пуассоновскими. Интенсивность поступления заявок равна , интенсивность обслуживания . СМО может находиться в следующих состояниях: · S0 - в СМО 0 заявок (все каналы свободны); · S1 - в СМО 1 заявка (один канал занят, остальные свободны); · Sk - в СМО n заявок (k каналов заняты, остальные свободны); · Sn - в СМО n заявок (все каналы заняты).  Рис. 171. ГСП многоканальной СМО с отказами Если система находится в состоянии S1, то поток, переводящий систему в состояние S0, будет иметь интенсивность μ. Если система находится в состоянии S2, то поток, переводящий систему в состояние S1, будет иметь интенсивность 2μ. (два канала порождают поток с интенсивностью в два раза большей). Если система находится в состоянии Sk, то поток, переводящий систему в состояние Sk-1, будет иметь интенсивность kμ. (k каналов порождают поток с интенсивностью в k раз большей). Процесс, показанный на рис. 17, представляет собой частный случай процесса гибели и размножения. Уравнения Колмогорова для вероятностей состояний системы P0 , P1 , ... , Pn будут иметь следующий вид: 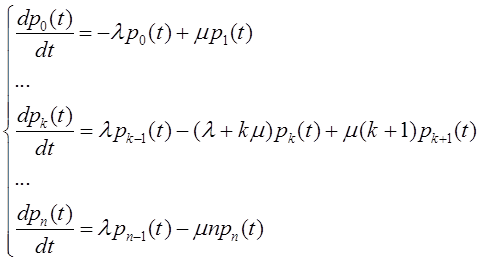 (4) (4)Предельные вероятности имеют вид 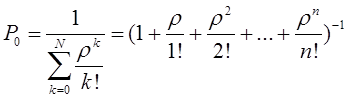  (5) (5)где  . .Соотношения  (5) называются формулами Эрланга. С их помощью можно найти предельные вероятности в зависимости от значений параметров λ и μ. Характеристики стационарного режима таковы. (5) называются формулами Эрланга. С их помощью можно найти предельные вероятности в зависимости от значений параметров λ и μ. Характеристики стационарного режима таковы.Вероятность отказа. Заявка получает отказ, если все каналы заняты. Вероятность этого равна:  (6) (6)Относительная пропускная способность есть вероятностьтого, что заявка будет принята к обслуживаниюи может быть найдена как дополнение Абсолютная пропускная способность находится как Среднее число заявок в системе (среднее число занятых каналов) можно вычислить через вероятности P0, P1, …, Pk,… Pn, по формуле как математическое ожидание дискретной случайной величины. Однако, проще выразить среднее число занятых каналов через абсолютную пропускную способность А, которая уже известна. Действительно, А есть среднее число заявок, обслуживаемых в единицу времени; один занятый канал обслуживает в среднем μ заявок в единицу времени; среднее число занятых каналов получается делением А на  или, переходя к обозначению  : :Посмотрим, как может применяться описанная модель для решения оптимизационной задачи проектирования системы. Пускай нам требуется определить наиболее предпочтительный (в смысле экономического эффекта) вариант многоканальной СМО с отказами. Для этого необходимо определить число обслуживающих приборовn, при котором достигается максимум функции где – величина получаемой прибыли; – получаемый в результате эксплуатации системы доход; – стоимость эксплуатации приборов (все величины приведены к единице времени). Будем искать решение при таких предположениях: · средний интервал времени между заявками в потоке ( ) составляет 5 мин; · заявка обрабатывается в среднем 5 мин ( ); · затраты на эксплуатацию одного прибора ( ) составляют 1 рублей/мин; · доход от одной обслуженной заявки ( ) равен 80 рублей. Значение функции Значение функции находится как произведение затрат на эксплуатацию одного прибора на число приборов: Поэтому, подставляя в Сначала определим значение :  Далее по формуле n=1: По формуле  (2) находим q (2) находим q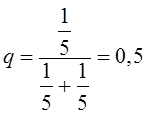 и по формуле 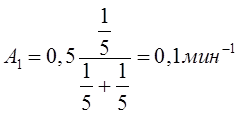 n=2: По формулам 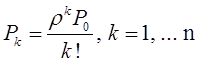 (5) находим сначала (5) находим сначала 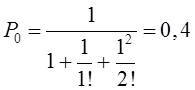 затем по формуле (6) 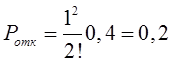 и по формуле 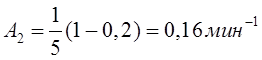 Аналогично получаем: n=3: 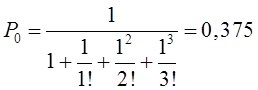 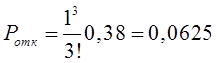 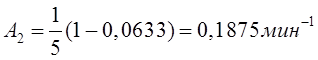 n=4: 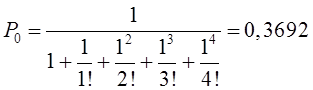 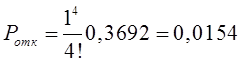 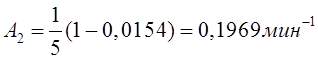 n=5: 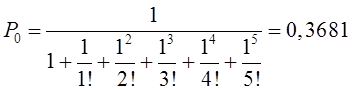 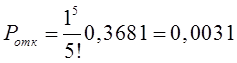 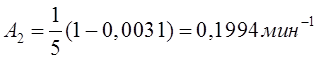 Подставляя найденные значения в График зависимости P от n имеет вид: 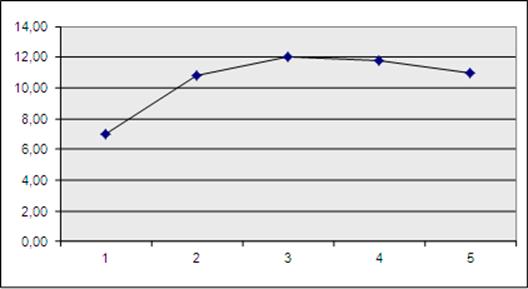 Рис. 18. Зависимость величины приведенной прибыли от числа приборов Как видим, максимум прибыли в единицу времени достигается для числа обслуживающих приборов равного трем. Вопрос 4. Обслуживание с очередями. В системах с ожиданием заявки, заставшие обслуживающий прибор в момент прихода занятым, в отличие от систем с отказами не покидают систему, а остаются ждать в очереди вместе с другими ждущими заявками (рис. 15). Для описания таких систем используются показатели, характеризующие длину очереди и время ожидания заявками обслуживания. В частности, если временной интервал между появлением заявок распределен по экспоненциальному закону (пуассоновский поток), то среднее время ожидания заявки в очереди можно найти по формуле Хинчина-Полачека: 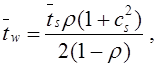 (12) (12)где — среднее время обслуживания заявки; σs— среднеквадратическое (стандартное) отклонение времени обслуживания в приборе; ρ — коэффициент использования прибора 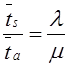 ; ;— средний интервал времени между поступлением заявок; cs — коэффициент вариации времени обслуживания Число заявок, ожидающих обслуживания (среднюю длина очереди), можно найти, умножив на величину λ: 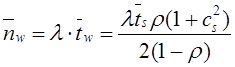 (13) (13)что, с учетом равенства дает 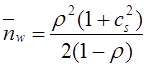 (14) (14)Формула Хинчина-Полачека используется для оценивания длин очередей при проектировании информационных систем. Она применяется в случае экспоненциального распределения времени поступления при любом распределении времени обслуживания и любой дисциплине управления, лишь бы выбор очередного сообщения для обслуживания не зависел от времени обслуживания. При проектировании систем встречаются такие ситуации возникновения очередей, когда дисциплина обслуживания выбирается в зависимости от времени обслуживания. Например, в некоторых случаях для первоочередного обслуживания могут выбираться более короткие сообщения с тем, чтобы получить меньшее среднее время обслуживания (среднее время пребывания в заявки системе). При управлении линией связи (каналом Интернет) можно присвоить входным сообщениям более высокий приоритет, чем выходным, поскольку первые короче. В таких случаях уже необходимо использовать не уравнение Хинчина — Поллачека или производные от него, а более сложные уравнения или использовать метод имитационного моделирования, рассматриваемы далее. Особый интерес для практических применений представляют два случая. 1) Время обслуживания постоянно. При регулярном характере потока рассеяние отсутствует, поэтому среднеквадратическое отклонение , и формулы (12), (13) преобразуются в выражения 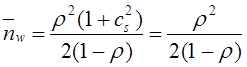 (15) (15)и 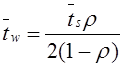 (16) (16)2)Время обслуживания имеет экспоненциальное распределение. В случае экспоненциального распределения, как известно, среднеквадратическое отклонение , поэтому (12), (13) принимают вид: 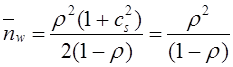 (17) (17)и 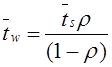 (18) (18)Большинство значений времени обслуживания в информационных системах лежит где-то между этими двумя значениями. Времена обслуживания, равные постоянной величине, встречаются редко. Даже время доступа к твердому диску непостоянно из-за различного положения массивов с данными на поверхности. Одним из примеров, иллюстрирующих случай постоянного времени обслуживания может служить занятие линии связи для передачи сообщений фиксированной длины. С другой стороны, разброс времени обслуживания обычно не так велик, как в случае произвольного или экспоненциального распределения, т.е., редко достигает значений . Этот случай иногда считают наихудшим и потому пользуются формулами, относящимися к экспоненциальному распределению времени обслуживания. Такой расчет может дать несколько завышенные размеры очередей и времен ожидания в них, но эта ошибка, по крайней мере, не опасна. Экспоненциальное распределение времен обслуживания не наихудший случай, с которым приходится иметь дело в действительности. Однако, если времена обслуживания, полученные при расчете очередей, оказываются распределенными хуже, чем времена с экспоненциальным распределением, то его можно рассматривать как предостережение разработчику. Если стандартное отклонение больше среднего значения, то обычно возникает необходимость в коррекции расчетов. Покажем, каким образом можно использовать формулу (13) для улучшения характеристик СМО. Пусть имеются шесть типов сообщений, требующих для своего обслуживания соответственно 15, 20, 25, 30, 35, 40 и 300 временных единиц. Число сообщений каждого типа одинаково. Стандартное отклонение указанных времен несколько выше их среднего. Значение последнего времени обслуживания намного больше других. Это приведет к тому, что сообщения будут находиться в очереди значительно дольше, чем, если бы времена обслуживания были одного порядка. В таком случае при проектировании целесообразно принять меры для уменьшения длины очереди. Например, если указанные значения связаны с длинами приходящих сообщений, то, возможно, очень длинные сообщения стоит разделить на части. Получим количественную оценку системных показателей для первоначального варианта организации информационного обмена и для двух вариантов, в которых длины сообщений передаваемых сообщений выровнены. Вычислим величины, входящие в формулу для средней длины очереди. Будем считать, что средняя продолжительность для всей группы сообщений составляет 600 временных единиц. Тогда коэффициент загрузки 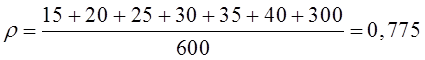 математическое ожидание времени обслуживания 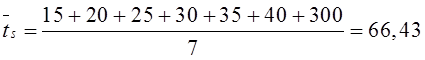 среднеквадратическое отклонение времени обслуживания 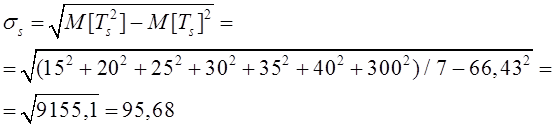 коэффициент вариации времени обслуживания 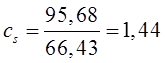 Подставляя в (13) получаем средний размер очереди в первоначальном варианте: 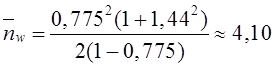 Вычислим теперь этот показатель для случая, когда последнее сообщение разбивается на два сообщения одинаковой длины. Поступая аналогичным образом, будем иметь (очевидно, что значение ρ остается тем же): 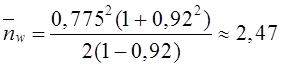 Разбивая длинное сообщение теперь уже на три части, получаем для средней длины очереди значение Видим, что прибегая к разбиению длинного сообщения на три сообщения одинаковой длины можно сократить среднюю длину образующейся в системе очереди более чем вдвое. Помимо моделей теории массового обслуживания для решения задач, связанных с анализом и проектированием информационных систем, структура которых может рассматриваться как СМО, применяются также и имитационные модели, которые рассматриваются далее. Вопрос 5. Многоканальная СМО сограниченной очередью. Входящий поток заявок на обслуживание - простейший поток с интенсивностью λ. Интенсивность потока обслуживания равна μ. Длительность обслуживания – случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Размер очереди допускает нахождение в ней m заявок. СМО может находиться в следующих состояниях: · S0 - в СМО 0 заявок (все каналы свободны, очереди нет); · S1 - в СМО 1 заявка (1 канал занят, очереди нет); · S2 - в СМО 2 заявки (2 канала заняты, очереди нет); · Sk - в СМО k заявок (k каналов заняты, очереди нет); · Sn - в СМО n заявок (n каналов занято, очереди нет); · Sn+1 - в СМО n+1 заявка (n каналов занято, 1 заявка в очереди); · Sn+r - в СМО n+r заявок (n каналов занято, r заявок в очереди); · Sn+m - в СМО n+ m заявок (n каналов занято, m заявок в очереди). ГСП системы показан на рис. 19. ГСП многоканальной СМО с ограниченной очередью: 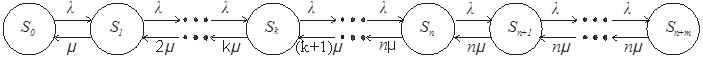 Рис. 19. ГСП многоканальной СМО с ограниченной очередью ГСП есть схема процесса размножения и гибели, для него можно использовать общее решение для предельных вероятностей. 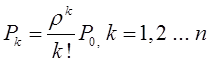 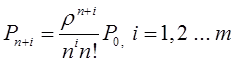 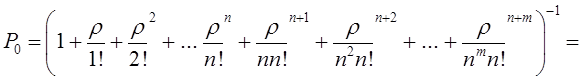 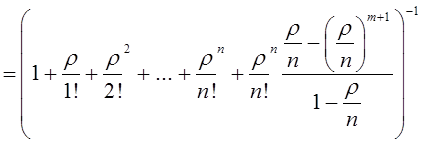 (19) (19)где 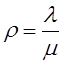 (использовано выражение для суммы геометрической прогрессии со знаменателем ). (использовано выражение для суммы геометрической прогрессии со знаменателем ).Вероятность отказа в обслуживании заявки. Отказ произойдет в случае, если все n каналов заняты и в очереди находятся m заявок: 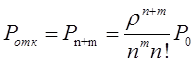 (20) (20)Относительная пропускная способность: 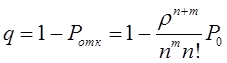 Абсолютная пропускная способность: 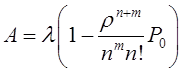 Среднее число занятых каналов. Для СМО с очередью среднее число занятых каналов не совпадает - в отличие от СМО с отказами - со средним числом заявок в системе. Отличие равно числу заявок, ожидающих в очереди. Каждый занятый канал обслуживает в среднем μ заявок в единицу времени, а СМО в целом – А заявок в единицу времени. Разделив А на μ получим 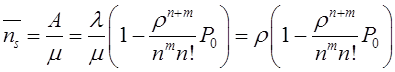 Среднее число находящихся в очереди заявок. Найдем среднее число ожидающих в очереди заявок: 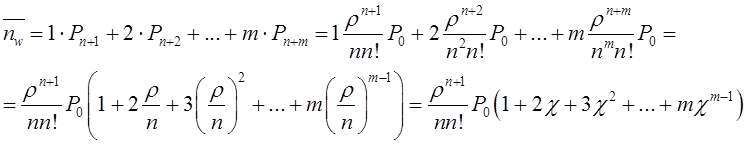 (21) (21)где = . Выражение в скобках можно трактовать (как и ранее) как производную по ρ от суммы геометрической прогрессии и получить выражение: 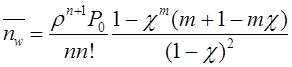 (22) (22)которым можно пользоваться во всех случаях кроме =0. Среднее число находящихся в системе заявок. Поскольку среднее число находящихся в системе заявок Среднее время ожидания заявки в очереди. Рассмотрим возможные ситуации, в которых пришедшая заявка может застать СМО. Если заявка приходит в систему в какой-то момент времени и какой-то канал не занят, то она не будет ждать в очереди. Если заявка приходит в систему в момент, когда заняты все каналы, а очереди нет, то она будет ждать в очереди в среднем 1/nμ (поток освобождения n каналов имеет интенсивность nμ). Если заявка приходит в систему в момент, когда заняты все каналы, а в очереди одну заявку, то она будет ждать в очереди в среднем 2/nμ (по 1/nμ на каждую впередистоящую заявку). Если заявка приходит в систему в момент, когда заняты все каналы, а в очереди стоят k заявок, то она будет ждать в очереди в среднем k/nμ. Если заявка приходит в систему в момент, когда заняты все каналы, а в очереди стоят m заявок, то она не будет ждать, так как покинет систему. Среднее время ожидания определим из выражения 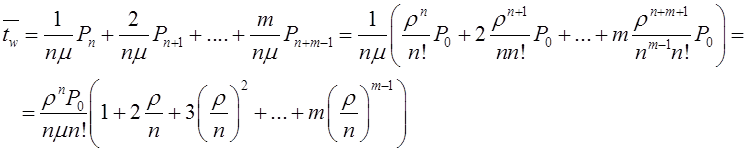 (23) (23)Это выражение отличается от выражения для средней длины очереди только множителем 1/ρμ=λ, откуда 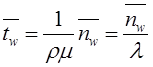 т.е., результат, вытекающий из формулы Литтла, или 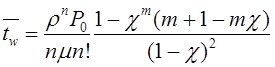 (24) (24)Среднее время пребывания заявки в системе. Так же как и в случае с одноканальной СМО имеем: 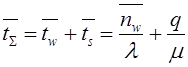 (25) (25)Пример 0‑1. В парикмахерской работают 3 мастера, для очереди посетителямив в зале ожидания предусмотрены 3 места. Клиенты приходят в среднем один раз в 4 минуты, обслуживание длится в среднем 15 мин. Требуется определить относительную и абсолютную пропускные способности парикмахерской, среднее число клиентов, ждущих обслуживани,я, и среднее время нахождения клиента в парикмахерской. Решение: Имеем: n=3, m=3, l=1/4=0,25, m=1/15, ρ =15/4=3,75, χ=ρ /n=1,25. Находим : 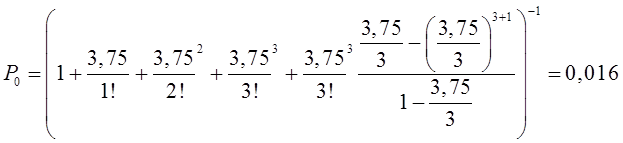 и вероятность отказа в обслуживании. 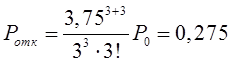 Относительная пропускная способность парикмахерской: Абсолютная пропускная способность: Среднюю длину очереди находим на основе формулы 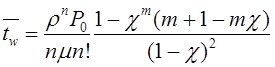 (24): (24):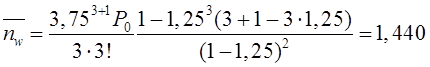 Среднее время нахождения клиента в парикмахерской определяется с помощью 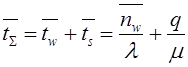 (25): (25):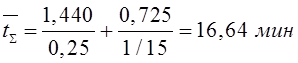 Выводы: 1. Многие задачи анализа и проектирования можно решить с использованием моделей систем массового обслуживания. Это дает возможность применять модели теории с тем же названием, многие из моделей которой получены на основе теории марковских процессов. 2. Основными показателям моделей систем с отказами являются относительная и абсолютная пропускная способность, а также вероятность отказа в обслуживании. Эти показатели для стационарного режима могут быть найдены на основе математических выражений. 3. Важными показателями для системы с ожиданием являются показатели, характеризующие нахождение заявок в очереди. Анализ таких систем может производиться в случае пуассоновского входящего потока на основе формулы Хинчина-Полачека. 4. Модели СМО можно применять для решения разнообразных практических задач. В частности, на примерах данной темы показано, как с помощью модели многоканальной СМО отказами можно решить задачу оптимизации числа каналов по критерию величины прибыли, а с помощью модели СМО с очередью определить требования к размерам заявок для уменьшения размера очереди и связанного с ней размера буферного накопителя. Вопросы для самопроверки: 1. Приведите примеры СМО с отказами. 2. Дайте краткое описание модели СМО с отказами. 3. Как получаются выражения для характеристик СМО с отказами? 4. Что такое относительная пропускная способность СМО с отказами? 5. Что такое абсолютная пропускная способность? 6. Как рассчитывается вероятность одноканальной СМО? 7. Как рассчитывается вероятность одноканальной СМО? 8. Чему равна вероятность отказа обслуживания заявки в многоканальной СМО с отказами? 9. Как подсчитывается среднее число заявок в многоканальной системе с отказами? 10. Как можно определить структуру (число каналов) многоканальной СМО по критерию максимума получаемой прибыли? 11. Какими показателями характеризуется функционирование одноканальной СМО с неограниченной очередью? 12. Что такое дисциплина обслуживания? Назовите примеры наиболее известных дисциплин. 13. Что позволяет определить формула Хинчина-Полачека? Для каких случаев справедлива формула? 14. Какие распределения времени обслуживания в одноканальной СМО с неограниченной очередью представляют наибольший интерес для практики? Опишите эти случаи. 15. Какие основные факторы влияют на значения показателей одноканальной СМО с неограниченной очередью? 16. Каким образом можно улучшить характеристики функционирования одноканальной СМО с неограниченной очередью? Литература по теме: 1. Емельянов А.А. Модели процессов массового обслуживания // Прикладная информатика, 2008, № 5 (17), с. 92-130. 2. Емельянов А.А. Стохастические сетевые модели массового обслуживания // Прикладная информатика, 2009, № 5 (23), с. 103-111. |
