Математическое моделирование. Документ Microsoft Word. исследование и оптимизация свойств локальных информационных систем
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
|
Тема 4. Моделирование марковских процессов Цели изучения темы: · познакомиться с понятием марковского процесса; · познакомиться с математическим аппаратом моделирования дискретно протекающих марковских процессов. Задачи изучения темы: · изучить способ математического описания марковских процессов; · научиться определять характеристики марковских процессов с дискретным временем и дискретным множеством состояний. Успешно изучив тему, Вы: получите представление о: · сущности марковских процессов и их классификации; · как формулируются задача в терминах марковского процесса; · способах построения математической модели и нахождения с ее помощью значений нужных показателей; будете знать: · как описать протекающие процессы с помощью графа состояний и переходов; · как найти вектор вероятностей состояния процесса на определенном шаге; · как вычислить предельные вероятности процесса. Вопросы темы: 1. Понятие марковского процесса. 2. Классификация марковских процессов. 3. Граф состояний и переходов. 4. Марковский процесс с дискретными состояниями и дискретным временем. 5. Предельные вероятности цепи Маркова. Вопрос 1. Понятие марковского процесса. Постановка многих задач анализа и, в особенности, проектирования систем связаны с необходимостью проведения оценивания количественных показателей протекающих в системе процессов. Часто поведение этих развивающихся во времени процессов в силу действия различных случайных факторов не удается исследовать во всех деталях. Следствием этого является невозможность в отличие от детерминированных систем однозначно предсказать поведение системы в какой-то момент в будущем. Такие системы и процессы носят название стохастических (от греческого στοχαστική – умеющий угадывать). Их анализ целесообразно проводить, рассматривая их как случайные процессы, ход и исход которых зависят от ряда случайных факторов, сопровождающих их развитие. Для нахождения числовых значений нужных параметров применяются как аналитические, так и имитационные модели. В настоящей и следующей теме будет рассмотрен подход на основе аналитических моделей. Построение аналитической модели в случае стохастических процессов означает необходимость построения некоторой вероятностной модели явления, в которой будут учтены обусловливающие его развитие случайные факторы. Для математического описания многих случайных процессов может быть применен аппарат, разработанный в теории вероятностей для так называемых марковских случайных процессов. Случайный процесс, протекающий в системе S, называется марковским (или процессом без последействия), если он обладает следующим свойством: для каждого момента времени t0 вероятность любого состояния системы в будущем (при t>t0) зависит только от ее состояния в настоящем (при t= t0) и не зависит от того, когда и каким образом система пришла в это состояние (т.е., как развивался процесс в прошлом). Другими словами, в марковском случайном процессе будущее развитие зависит только от его настоящего состояния и не зависит от «предыстории» процесса. Вопрос 2. Классификация марковских процессов. Марковские случайные процессы делятся на классы. Основными классифицирующими признаками являются: · множество состояний, в которых может находиться система; · моменты времени, в которых происходит изменение состояния системы. Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы S1, S2, S3, ... можно перечислить (перенумеровать) одно за другим, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) переходит из одного состояния в другое. Кроме процессов с дискретными состояниями существуют случайные процессы с непрерывными состояниями: для этих процессов характерен постепенный, плавный переход из состояния в состояние. Например, процесс изменения напряжения в осветительной сети представляет собой случайный процесс с непрерывными состояниями. Если переходы системы из состояния в состояние возможны только в определенные моменты времени t1, t2, t3, … , то марковский процесс относится к процессам с дискретным временем. В противном случае имеет место процесс с непрерывным временем. Вопрос 3. Граф состояний и переходов. Анализ случайных процессов с дискретными состояниями обычно проводится с помощью графа состояний и переходов (ГСП). Пусть имеется система S с n дискретными состояниями: S1, S2, S3 , … , Sn Каждое состояние изображается окружностью или прямоугольником (вершина), а возможные переходы из состояния в состояние («перескоки») — стрелками (дугами), соединяющими эти вершины (рис. 8а). 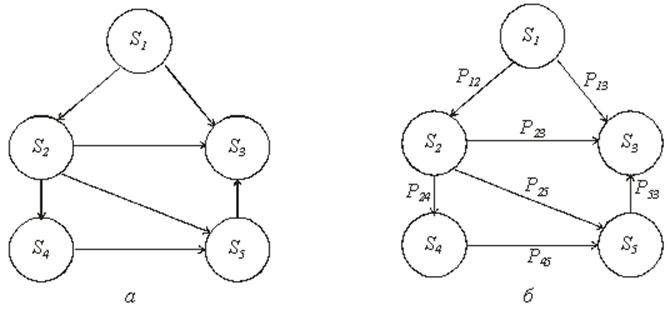 Рис. 8. Пример неразмеченного (а) и размеченного (б) ГСП Заметим, что стрелками можно отмечать только непосредственные переходы из состояния в состояние; если система может перейти из состояния S1в S5только через S2, то стрелками отмечаются только переходы S1—S2 и S2—S5, но не S1—S5. Удобно также пользоваться размеченным графом, который графически изображает не только возможные состояния системы и возможные переходы из состояния в состояние, но также и значения вероятностей перехода (рис. 8 б), о которых речь будет идти ниже. Вопрос 4. Марковский процесс с дискретными состояниями и дискретным временем. Пусть система S может находиться в состояниях: S1, S2, S3, … , Sn и изменения состояния системы возможны только в моменты: t1, t2, t3, … , tn Будем называть эти моменты шагами, или этапами процесса и рассматривать протекающий в системе S случайный процесс как функцию целочисленного аргумента m = 1, 2, ... k, ... , обозначающего номер шага. Указанный случайный процесс состоит в том, что в последовательные моменты времени t1, t2, ... , tk, ... система S оказывается в тех или иных состояниях. Процесс, происходящий в системе, можно представить как последовательность (цепочку) событий, например: называемую марковской цепью, где для каждого шага вероятность перехода из любого состояния Si в любое Sjне зависит от того, когда и как система пришла в состояние Si . Марковскую цепь можно описать с помощью вероятностей состояний, в которых находится система на каком-то шаге. Пусть в любой момент времени (после любого шага) система может пребывать в одном из состояний: S1, S2, S3, … , Sn т.е., в результате шага k осуществится одно из полной группы несовместных событий: Обозначив вероятности этих событий для k -го шага через легко видеть, что для каждого шага k поскольку Вероятности Для любого шага (момента времени t1, t2, ... tk, ... или номера 1, 2, ... , k, ...) существуют некоторые вероятности перехода системы из любого состояния в любое другое (некоторые из них равны нулю, если непосредственный переход за один шаг невозможен), а также вероятность задержки системы в данном состоянии. Эти вероятностиназываются переходными вероятностями марковской цепи. Если значения переходных вероятностей не зависят от номера шага, то марковская цепь называется однородной, или стационарной. В противном случае марковская цепь является неоднородной, или нестационарной. Если из состояния Si не исходит ни одной стрелки (переход из него ни в какое другое состояние невозможен, например, S3 графа рис. 8), соответствующая вероятность задержки Рii равна единице. Графу системы, содержащему n вершин, можно поставить в соответствие матрицу n×n, элементами которой являются вероятности переходов pij между вершинами графа, называемую матрицей вероятностей переходов: 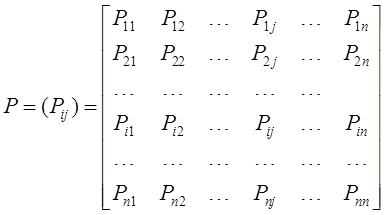 (1) (1)Элементы матрицы переходов, означающие вероятности переходов в системе за один шаг, удовлетворяют условиям: 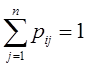 (3) (3)Условие (2) выражает ограничение, накладываемое на значение вероятности, а условие (3) означает, что система S обязательно либо переходит из какого-то состояния Si в другое состояние, либо остается в состоянии Si (иначе говоря, события Обычно на графе вероятности перехода системы из одного состояния в то же самое не отмечаются, так как каждая из них дополняет до единицы сумму переходных вероятностей, соответствующих всем стрелкам, исходящим из данного состояния. Например, для графа рис. 8 б значения переходных вероятностей будут равны: При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы. Имея размеченный ГСП (или, что равносильно, матрицу переходных вероятностей) и зная начальное состояние системы, можно найти вероятности состояний р1(k), р2(k), ... , рn(k) после любого (k-го) шага. Они находятся с помощью следующих рекуррентных соотношений: 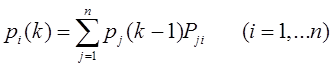 (4) (4)или в матричной форме где , - матрица переходных вероятностей. Предположим, что в начальный момент (перед первым шагом) система находится в каком-то определенном состоянии, например Sm. Тогда для начального момента (0) будем иметь: р1(0) =0, р2(0) =0, ..., рm(0) = 1, ... , рn(0) = 0 , т. е. вероятности всех состояний равны нулю, кроме вероятности начального состояния Sm, равной единице. Найдем вероятности состояний после первого шага. Мы знаем, что перед первым шагом система заведомо находится в состоянии Sm. Значит, за первый шаг она перейдет в состояния S1, S2, ... , Sm, ... , Sn с вероятностями Pm1, Pm2, ... , Pmm, ... , Pmn , находящимися в m-ой строке матрицы переходных вероятностей. Таким образом, вероятности состояний после первого шага будут: Найдем вероятности состояний после второго шага: Вычислим их по формуле полной вероятности с гипотезами: · после первого шага система была в состоянии S1; · после первого шага система была в состоянии S2; · после первого шага система была в состоянии Si; · после первого шага система была в состоянии Sn. Вероятности гипотез известны (6), условные вероятности перехода в состояние Si - при каждой гипотезе тоже известны и записаны в матрице переходных вероятностей. По формуле полной вероятности получим: 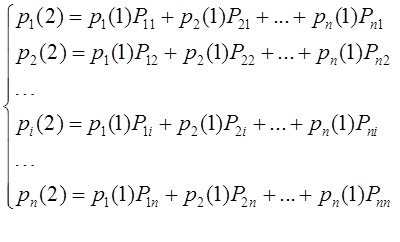 (7) (7)или 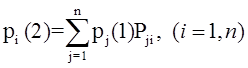 (8) (8)Данное выражение может быть записано в векторно-матричной форме: В формулах (7) – 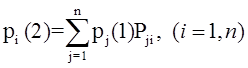 (8) суммирование распространяется формально на все состояния S1, S2, ... , Sm, ... , Sn ; фактически учитывать надо только те из них, для которых переходные вероятности Pij отличны от нуля, т.е. те состояния, из которых может совершиться переход в состояние Sl (или задержка в нем). (8) суммирование распространяется формально на все состояния S1, S2, ... , Sm, ... , Sn ; фактически учитывать надо только те из них, для которых переходные вероятности Pij отличны от нуля, т.е. те состояния, из которых может совершиться переход в состояние Sl (или задержка в нем).Таким образом, вероятности состояний после второго шага известны. Очевидно, после третьего шага они определяются аналогично: 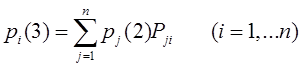 (10) (10)И вообще после k-то шага: 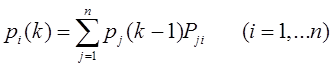 (11) (11)Или в матричной форме Таким образом, вероятности Например, пусть требуется найти вероятность перехода системы из состояния S1 в состояние S2 за 3 шага для графа на рис. 9. 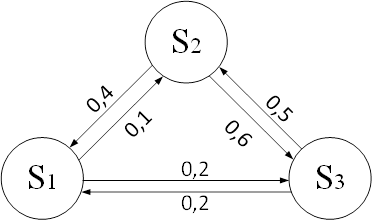 Рис. 9. Пример ГСП Из условия следует, что Вероятности состояния после второго шага: Вероятность состояния S2 после третьего шага Если обозначить через где матрица получается умножением матрицы P саму на себя m раз. Пусть исходное состояние системы задается вектором : где pi, i=1, … n есть вероятность того, что в начальный момент система находится в состоянии Si. Тогда для нахождения вектора вероятностей состояния системы после m шагов можно воспользоваться формулой: Воспользуемся приведенными формулами для нахождения вектора состояния системы, изображенной рис. 9, после двух шагов, для случая, когда исходное состояние системы задается вектором С помощью формулы 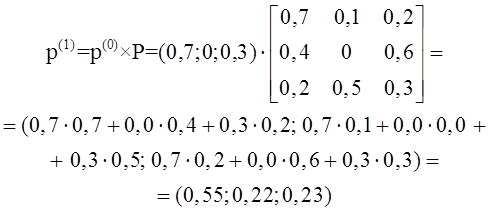 и состояние системы после второго шага 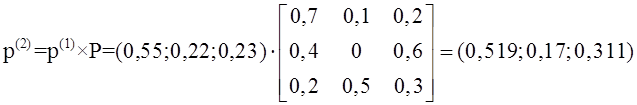 Тот же результат получается с помощью формулы 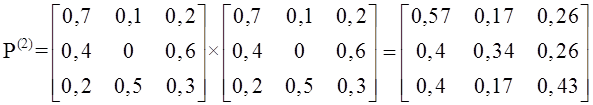 находим: 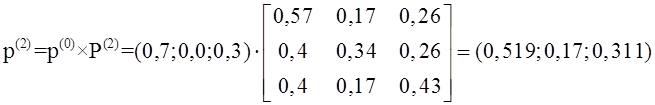 Вопрос 5. Предельные вероятности цепи Маркова. Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими. Если при некотором n все элементы матрицы Р не равны нулю, то такая матрица переходов называется регулярной. Другими словами, регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через n шагов из любого состояния. Такие цепи Маркова так же называются регулярными. Известно (теорема о предельных вероятностях), что для регулярной цепи Маркова с n состояниями и матрицей вероятностей перехода Р существует предел и матрица 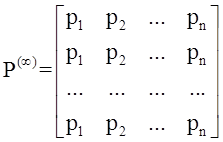 т.е. состоит из одинаковых строк. Величины p1, p2, … , pn называются предельными вероятностями. Эти вероятности не зависят от исходного состояния системы, и вектор вероятности полностью определяется из условий: 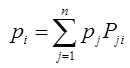 ) )и условия нормировки Пусть требуется найти предельные вероятности для матрицы переходов 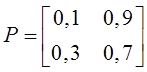 Так как и матрица предельных вероятностей: 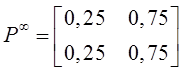 Выводы: 1. Решение многих задач, связанных с анализом процессов и создания систем, основано на рассмотрении протекающих процессов как стохастических. Для оценивания показателей этих процессов и систем применяются аналитические модели. 2. Важным классом случайных процессов является марковский процесс. Марковские процессы протекают в отсутствие предыстории, что значительно упрощает их математическое описание. 3. Для описания процесса с дискретным временем и дискретными состояниями используются граф переходов и состояний, а также связанная с ним матрица переходных вероятностей. На основе этих элементов можно найти вероятности нахождения процесса в каждом из своих состояний после любого шага, для чего применяются рекуррентные или матричные выражения, которые получены на основе формулы полной вероятности. 4. В случае регулярных цепей Маркова процесс обладает предельными вероятностями нахождения в каждом из своих состояний. Эти вероятности не зависят от номера шага и могут быть найдены путем решения системы линейных уравнений, получаемой из выражения для предельных вероятностей и нормировочного условия. Вопросы для самопроверки: 1. Что такое стохастическая система? 2. Какой процесс называется марковским? 3. Как классифицируются марковские процессы? 4. Дайте определение марковского процесса с непрерывным временем и дискретными состояниями. 5. Что такое однородный марковский процесс? 6. Что такое граф состояний и переходов (ГСП) Марковской цепи? Какие бывают ГСП? 7. Что понимается под матрицей переходных вероятностей? 8. Как можно найти вероятность нахождения процесса в определенном состоянии после определенного числа шагов? 9. Что такое нестационарная марковская цепь? 10. Что такое предельные вероятности марковского процесса? 11. Каков физический смысл предельных вероятностей? 12. При каких условиях существуют предельные вероятности состояний марковского процесса? 13. Как найти предельные вероятности системы, имеющей стационарный режим? Литература по теме: 1. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с. 2. Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. – М.: Финансы. 3. Саати Т.Л. Элементы теории массового обслуживания и её приложения. – М.: Радио и связь, 1965. – 512 с. |
