Лекция(Как найти обратную матрицу). Некоторые свойства операций над матрицами. Матричные выражения
 Скачать 150.08 Kb. Скачать 150.08 Kb.
|
|
Некоторые свойства операций над матрицами. Матричные выражения Вернёмся к действиям с матрицами. Можно ли к матрице прибавить число? Например: Матрицу можно умножить на число. Но сложить их нельзя. Следует отметить, что допустимо сложение определителя матрицы с числом: Результат вычисления определителя – число (справедливо и для разности). Как возвести матрицу в квадрат? Операция определена только для квадратных матриц – «два на два», «три на три» и т.д. Возвести квадратную матрицу Пример 1 Возвести в квадрат матрицу 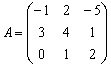 Решение:  – последовательно (слева направо) перебираем столбцывторой матрицы и «пристраиваем» их к каждой строке первой матрицы. Ответ: 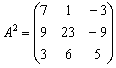 Немного о некоммутативности матричного умножения и единичной матрице Коммутативность = Перестановочность. Обычные числа переставлять можно Справедливо следующее свойство: если произвольную матрицу Коммутативность числового множителя относительно умножения матриц Для матриц То есть числовой множитель можно (и нужно) вынести вперёд. Правило остаётся справедливым, если перемножаются три либо большее количество матриц. Пример 2 Вычислить произведение Решение: 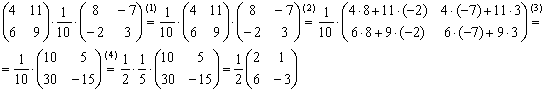 (1) Согласно свойству (2) – (3) Выполняем матричное умножение. (4) Здесь можно поделить каждое число 10, но тогда среди элементов матрицы появятся десятичные дроби, что не есть хорошо. Однако замечаем, что все числа матрицы делятся на 5, поэтому умножаем каждый элемент на Окончательный ответ лучше оставить в виде 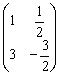 . Ответ: . Ответ: Как умножить три матрицы? Произведение трёх матриц 1) найти 2) либо сначала найти Результаты обязательно совпадут, и в теории данное свойство называют ассоциативностью матричного умножения: Пример 3 Перемножить матрицы двумя способами Алгоритм решения двухшаговый: находим произведение двух матриц, затем снова находим произведение двух матриц. 1) Используем формулу Действие второе: 2) Используем формулу Действие второе: Ответ: Как возвести матрицу в куб и более высокие степени? Данные операции также определены только для квадратных матриц. Чтобы возвести квадратную матрицу Фактически это частный случай умножения трёх матриц, по свойству ассоциативности матричного умножения: Пример 4 Возвести матрицу Решение: Сначала возведём матрицу в квадрат: Возведём матрицу в куб: Возведём матрицу в четвёртую степень двумя способами: Ответ: Матричные выражения Рассмотрим матричное выражение В первом слагаемом Во втором слагаемом С третьим слагаемым Если матричное выражение имеет смысл, то результат его вычисления является матрицей. Пример 5 Вычислить значение матричного многочлена 1) 2) 3) 4) 5) Примечание: выражение можно было вычислить и по-другому – предварительно раскрыть скобки: Как найти обратную матрицу? Что такое обратная матрица? Здесь можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему число Существует два основных метода нахождения обратной матрицы: с помощью алгебраических дополнений и с помощью элементарных преобразований. Рассмотрим квадратную матрицу Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д. Обозначения: обратная матрица обозначается надстрочным индексом Пример 6: Найти обратную матрицу для матрицы 1) Сначала находим определитель матрицы. Если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ. В рассматриваемом примере 2) Находим матрицу миноров Сначала рассмотрим левый верхний элемент: 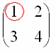 Как найти его минор? А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: 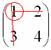 Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров: Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров: 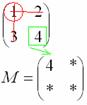 Рассматриваем следующий элемент матрицы Рассматриваем следующий элемент матрицы 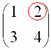 Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент: Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент: 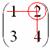 То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу: То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу: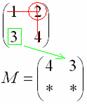 Аналогично рассматриваем элементы второй строки и находим их миноры: 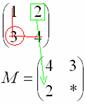 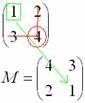 3) Находим матрицу алгебраических дополнений 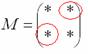 4) Находим транспонированную матрицу алгебраических дополнений 5) Ответ. Вспоминаем нашу формулу Необходимо выполнить матричное умножение Проверка: 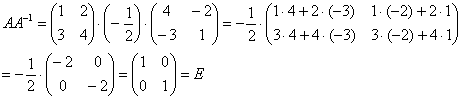 Получена единичная матрица– это матрица с единицами на главной диагонали и нулями в остальных местах. Таким образом, обратная матрица найдена правильно. Пример7: Найти обратную матрицу для матрицы 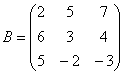 Алгоритм точно такой же, как и для случая «два на два». Обратную матрицу найдем по формуле: 1) Находим определитель матрицы. 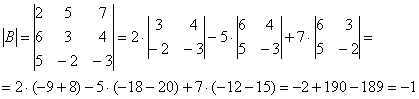 Здесь определитель раскрыт по первой строке. 2) Находим матрицу миноров 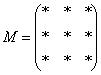 , и нам нужно найти девять чисел. Рассмотрим несколько миноров: , и нам нужно найти девять чисел. Рассмотрим несколько миноров:Рассмотрим следующий элемент матрицы: 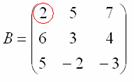 МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: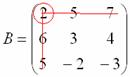 Оставшиеся четыре числа записываем в определитель «два на два» Оставшиеся четыре числа записываем в определитель «два на два»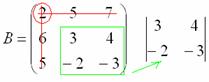 Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить: Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить: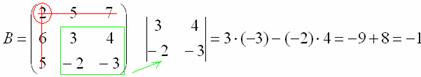 минор найден, записываем его в нашу матрицу миноров: минор найден, записываем его в нашу матрицу миноров: 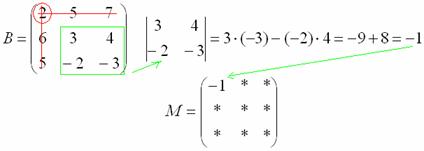 необходимо вычислить девять определителей «два на два». Найдем еще один минор в картинках: 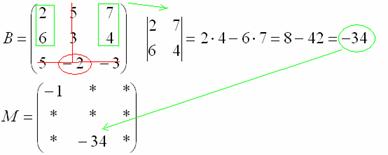 Остальные миноры вычислить самостоятельно. Окончательный результат: решаем самостоятельно– матрица миноров соответствующих элементов матрицы 3) Находим матрицу алгебраических дополнений В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов: 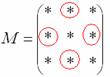 В данном случае: В данном случае:  – матрица алгебраических дополнений соответствующих элементов матрицы – матрица алгебраических дополнений соответствующих элементов матрицы 4) Находим транспонированную матрицу алгебраических дополнений 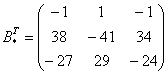 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 5) Ответ: 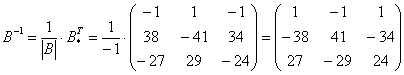 Проверка: 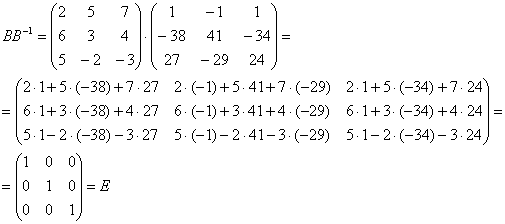 |
