Шпора теория ЛА. 1 Матрицы. Действия над матрицами Матрицей
 Скачать 182.28 Kb. Скачать 182.28 Kb.
|
|
1.1. Матрицы. Действия над матрицами Матрицей размерности 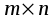 называется прямоугольная таблица, состоящая из называется прямоугольная таблица, состоящая из 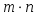 элементов, расположенных в m строках и n столбцах. элементов, расположенных в m строках и n столбцах. Элементы матрицы 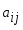 (первый индекс i − номер строки, второй индекс j − номер столбца) могут быть числами, функциями и т. п. Матрицы обозначают заглавными буквами латинского алфавита. (первый индекс i − номер строки, второй индекс j − номер столбца) могут быть числами, функциями и т. п. Матрицы обозначают заглавными буквами латинского алфавита.Матрица называется квадратной, если у нее число строк равно числу столбцов (m = n). В этом случае число n называется порядком матрицы, а сама матрица называется матрицей n-го порядка. Элементы с одинаковыми индексами 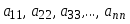 образуют главную диагональ квадратной матрицы, а элементы образуют главную диагональ квадратной матрицы, а элементы 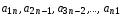 (т.е. имеющие сумму индексов, равную n+1) − побочную диагональ. (т.е. имеющие сумму индексов, равную n+1) − побочную диагональ.Единичной матрицей называется квадратная матрица, все элементы главной диагонали которой равны 1, а остальные элементы равны 0. Она обозначается буквой Е. Нулевая матрица − это матрица, все элементы которой равны 0. Нулевая матрица может быть любого размера. К числу линейных операций над матрицами относятся: 1) сложение матриц; 2) умножение матриц на число. Операция сложения матриц определена только для матриц одинаковой размерности. Суммой двух матриц А и В называется матрица С, все элементы которой равны суммам соответствующих элементов матриц А и В: 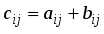 . .Произведением матрицы А на число k называется матрица В, все элементы которой равны соответствующим элементам данной матрицы А, умноженным на число k: 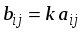 . .Операция умножения матриц вводится для матриц, удовлетворяющих условию: число столбцов первой матрицы равно числу строк второй. Произведением матрицы А размерности 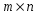 на матрицу В размерности на матрицу В размерности 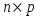 называется матрица С размерности называется матрица С размерности 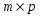 , элемент i-ой строки и j-го столбца которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В: , элемент i-ой строки и j-го столбца которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В: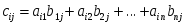 . .Произведение матриц (в отличие от произведения действительных чисел) не подчиняется переместительному закону, т.е. в общем случае А В 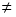 В А. В А.1.2. Определители. Свойства определителей Понятие определителя вводится только для квадратных матриц. Определителем матрицы 2-го порядка 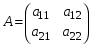 называется число, вычисляемое по следующему правилу называется число, вычисляемое по следующему правилу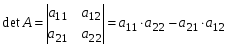 . .Определителем матрицы 3-го порядка 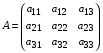 называется число, вычисляемое по следующему правилу: называется число, вычисляемое по следующему правилу: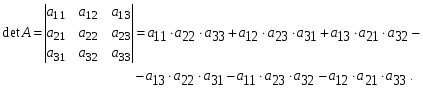 Первое из слагаемых со знаком «+» представляет собой произведение элементов, расположенных на главной диагонали матрицы ( 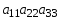 ). Остальные два содержат элементы, расположенные в вершинах треугольников с основанием, параллельным главной диагонали ( ). Остальные два содержат элементы, расположенные в вершинах треугольников с основанием, параллельным главной диагонали (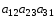 и и 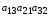 ). Со знаком «-» входят произведения элементов побочной диагонали ( ). Со знаком «-» входят произведения элементов побочной диагонали (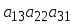 ) и элементов, образующих треугольники с основаниями, параллельными этой диагонали ( ) и элементов, образующих треугольники с основаниями, параллельными этой диагонали (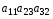 и и 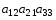 ). ).Это правило вычисления определителя 3-го порядка называется правилом треугольников (или правилом Саррюса). Свойства определителей рассмотрим на примере определителей 3-го порядка. 1. При замене всех строк определителя на столбцы с теми же номерами, что и строки, определитель своего значения не меняет, т.е. строки и столбцы определителя равноправны 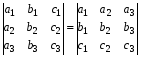 . .2. При перестановке двух строк (столбцов) определитель меняет свой знак. 3. Если все элементы некоторой строки (столбца) нули, то определитель равен 0. 4. Общий множитель всех элементов строки (столбца) можно вынести за знак определителя. 5. Определитель, содержащий две одинаковые строки (столбца), равен 0. 6. Определитель, содержащий две пропорциональные строки (столбца), равен нулю. 7. Если каждый элемент некоторого столбца (строки) определителя представляет сумму двух слагаемых, то определитель равен сумме двух определителей, в одном из которых в том же столбце (строке) стоят первые слагаемые, а в другом − вторые. Остальные элементы у обоих определителей одинаковые. Так, 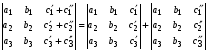 . .8. Определитель не изменится, если к элементам какого-либо его столбца (строки) прибавить соответствующие элементы другого столбца (строки), умноженные на одно и то же число. Следующее свойство определителя связано с понятиями минора и алгебраического дополнения. Минором элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, на пересечении которых этот элемент расположен. Например, минором элемента 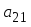 определителя определителя 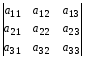 называется определитель называется определитель 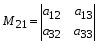 . .Алгебраическим дополнением элемента 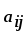 определителя называется его минор, умноженный на определителя называется его минор, умноженный на 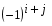 , где i − номер строки, j − номер столбца, на пересечении которых находится элемент , где i − номер строки, j − номер столбца, на пересечении которых находится элемент 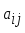 . Алгебраическое дополнение обычно обозначается . Алгебраическое дополнение обычно обозначается 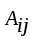 . Для элемента . Для элемента 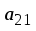 определителя 3-го порядка алгебраическое дополнение определителя 3-го порядка алгебраическое дополнение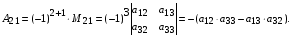 9. Определитель равен сумме произведений элементов какой-либо строки (столбца) на соответствующие им алгебраические дополнения. Например, определитель можно разложить по элементам первой строки 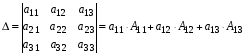 , ,или второго столбца 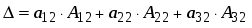 . .Свойства определителей применяются для их вычисления. 1.3. Применение определителей к решению систем линейных алгебраических уравнений. Правило Крамера Рассмотрим систему трех линейных алгебраических уравнений с тремя неизвестными: 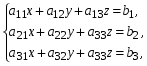 где 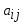 − коэффициенты при неизвестных; x, y, z − неизвестные, − коэффициенты при неизвестных; x, y, z − неизвестные, 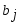 − свободные члены уравнений (i, j = 1, 2, 3). − свободные члены уравнений (i, j = 1, 2, 3).Решением системы называется любая совокупность значений неизвестных, подстановка которых в каждое уравнение системы превращает его в верное равенство (тождество). Система уравнений, имеющая хотя бы одно решение, называется совместной. Система уравнений, не имеющая ни одного решения, называется несовместной. Совместная система называется определенной, если она имеет только одно решение, и неопределенной, если у нее больше одного решения. Определителем системы (основным определителем) называется определитель, составленный из коэффициентов при неизвестных. Правило Крамера: а) если определитель системы трех уравнений с тремя неизвестными отличен от нуля, то эта система имеет единственное решение, которое вычисляется по формулам 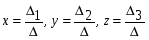 , ,где 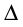 − определитель системы, − определитель системы, 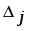 (j = 1, 2, 3) − определитель, отличающийся от определителя системы тем, что в нем i-й столбец заменен столбцом свободных членов уравнений системы; (j = 1, 2, 3) − определитель, отличающийся от определителя системы тем, что в нем i-й столбец заменен столбцом свободных членов уравнений системы;б) если определитель системы 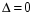 , но хотя бы один из определителей , но хотя бы один из определителей 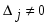 , то система решения не имеет (несовместна); , то система решения не имеет (несовместна);в) если определитель системы 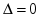 и все определители и все определители 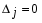 (j = 1, 2, 3), то система либо несовместна, либо имеет бесчисленное множество решений. (j = 1, 2, 3), то система либо несовместна, либо имеет бесчисленное множество решений.Правило Крамера справедливо и для системы из n уравнений с n неизвестными, т.е. для системы вида 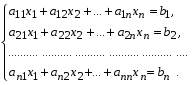 В этом случае, если 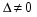 , то , то 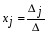 (j = 1, 2, 3,…, n). (j = 1, 2, 3,…, n).1.4. Матричный способ решения систем линейных алгебраических уравнений Квадратная матрица называется невырожденной, если ее определитель отличен от 0. В противном случае (т.е. когда определитель матрицы равен 0) матрица называется вырожденной. Матрица 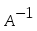 называется обратной матрице называется обратной матрице 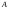 , если для нее выполняется условие , если для нее выполняется условие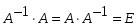 . .где Е − единичная матрица того же порядка, что и матрица 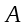 . .Для того чтобы матрица А имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной. Рассмотрим процесс построения обратной матрицы для матрицы 3-го порядка: 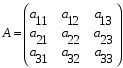 . .Вычисляем определитель det A этой матрицы. Он должен быть отличен от нуля. Затем находим алгебраические дополнения элементов матрицы А (А11, А12, ..., Аnn). Из них строим присоединенную матрицу 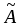 по следующему правилу: алгебраические дополнения элементов строк матрицы А составляют соответствующие столбцы матрицы по следующему правилу: алгебраические дополнения элементов строк матрицы А составляют соответствующие столбцы матрицы 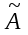 : :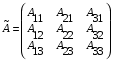 . .Обратную матрицу получаем по формуле: 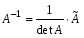 . .Для матрицы А размерности 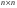 обратная матрица имеет вид: обратная матрица имеет вид: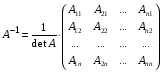 Рассмотрим систему n линейных алгебраических уравнений с n неизвестными: 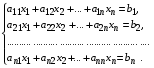 Построим следующие матрицы: 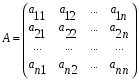 , , 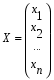 , , 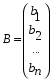 . .Здесь А − основная матрица системы, X − матрица-столбец неизвестных, В − матрица-столбец свободных членов уравнений системы. Тогда, используя операцию умножения матриц, данную систему можно представить в матричном виде 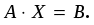 Пусть 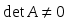 , тогда для матрицы , тогда для матрицы 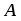 существует обратная матрица существует обратная матрица 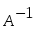 . .Для нахождения элементов неизвестной матрицы 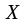 умножим слева полученное матричное уравнение на матрицу умножим слева полученное матричное уравнение на матрицу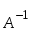 : :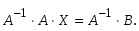 Так как 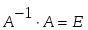 , а , а 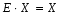 , то получим , то получим 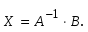 1.5. Общий случай линейной алгебраической системы уравнений. Условие совместности Ранг матрицы Определитель k-го порядка, составленный из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы А, называется минором k-го порядка, порожденным данной матрицей. Например, для матрицы А 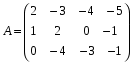 минор второго порядка можно получить, выбрав 1 и 3 строки, а также 1-й и 4-й столбцы: 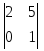 . .  Очевидно, что минорами, порожденными этой матрицей, являются и другие определители 2-го порядка: Очевидно, что минорами, порожденными этой матрицей, являются и другие определители 2-го порядка: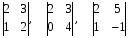 и т.д. и т.д.Данная матрица имеет минорами и определители 3-го порядка 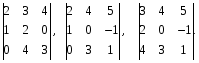 Рангом матрицы А (обозначается 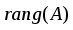 ) называется наивысший порядок отличных от нуля миноров, порожденных этой матрицей. ) называется наивысший порядок отличных от нуля миноров, порожденных этой матрицей.В рассматриваемой матрице А наивысший порядок ее миноров равен трем. Вычислим один из них. 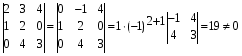 Так как этот минор отличен 0, то 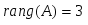 . .Вычислять все миноры, порождаемые данной матрицей, затруднительно. Поэтому для определения ранга матрицы можно использовать метод приведения матрицы к ступенчатому виду с помощью элементарных преобразований. Элементарными преобразованиями матрицы называются: 1) умножение какой-либо строки (столбца) на число 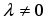 , ,2) перестановка двух строк (столбцов), 3) прибавление к элементам одной строки (столбца) соответственных элементов другой строки (столбца), умноженных на одно и то же число 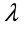 . .Элементарные преобразования не меняют ранг матрицы. Две матрицы называются эквивалентными, если одна из них получена из другой при помощи элементарных преобразований. Эквивалентные матрицы имеют один и тот же ранг. С помощью эквивалентных преобразований матрицу можно привести к ступенчатому виду. Матрица называется ступенчатой, если в ее первой строке имеется хотя бы один элемент отличный от 0, а в каждой последующей строке первый отличный от 0 элемент стоит правее первого отличного от 0 элемента предыдущей строки. Например, 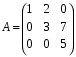 . .Ранг ступенчатой матрицы равен числу ее ненулевых строк. Для определения ранга матрицы нужно, применяя элементарные преобразования, привести ее к ступенчатому виду. Исследование на совместность систем линейных алгебраических уравнений Рассмотрим систему m линейных алгебраических уравнений с n неизвестными x1, x2, …, xn: 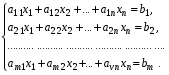 Составим две матрицы: 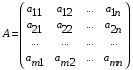 и и 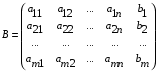 , ,где А − основная матрица системы, В − расширенная матрица системы. Условие совместности любой линейной алгебраической системы определяется теоремой Кронекера-Капелли: для того, чтобы линейная алгебраическая система уравнений была совместна необходимо и достаточно, чтобы ранг основной матрицы системы равнялся рангу расширенной матрицы системы, т. е. 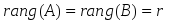 . .При этом возможны два случая: а) 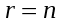 , тогда система имеет единственное решение; , тогда система имеет единственное решение;б) 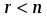 , тогда система имеет бесконечное множество решений (при этом r неизвестных являются основными, остальные n - r неизвестных – свободными, им можно придавать произвольные значения, в зависимости от которых принимают значения основные переменные). , тогда система имеет бесконечное множество решений (при этом r неизвестных являются основными, остальные n - r неизвестных – свободными, им можно придавать произвольные значения, в зависимости от которых принимают значения основные переменные).1.6. Метод Гаусса решения систем линейных алгебраических уравнений Основная идея метода Гаусса − последовательное исключение неизвестных. Решение системы линейных алгебраических уравнений методом Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому виду. На втором этапе (обратный ход) идет последовательное определение неизвестных из ступенчатой системы. На практике удобнее работать не с системой, а с ее расширенной матрицей, выполняя элементарные преобразования над ее строками. Сущность метода проиллюстрируем на примере решения системы из трех уравнений с тремя неизвестными. Таким образом, если число уравнений в полученной ступенчатой системе равно числу неизвестных, то система имеет единственное решение. Все неизвестные в этом случае определяются последовательно, начиная с последнего. Если же число уравнений в ступенчатой системе меньше числа неизвестных ( 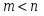 ), то система имеет бесконечное множество решений. В этом случае неизвестные x1, x2,…, xn могут быть выражены через ), то система имеет бесконечное множество решений. В этом случае неизвестные x1, x2,…, xn могут быть выражены через 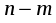 остальные неизвестные. остальные неизвестные.Система не имеет решений, если одно из уравнений имеет отличный от нуля свободный член, а все коэффициенты в левой части равны нулю, т. е. если при преобразованиях получаются уравнения вида 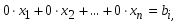 где где 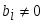 . .Этому случаю соответствует появление в ступенчатой матрице строки вида 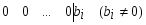 . . |
