Математическое моделирование. Документ Microsoft Word. исследование и оптимизация свойств локальных информационных систем
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
|
Тема 3. Пуассоновский поток и проверка статистических гипотез Цели изучения темы: · познакомиться с пуассоновским потоком заявок, имеющим большое значения для моделирования широкого класса систем и процессов; · изучить математический аппарат проверки гипотез для решения задач этапов сбора данных и обработки результатов моделирования. Задачи изучения темы: · познакомиться с постановкой задачи проверки статистических гипотез применительно к их использованию в моделировании; · понять какие свойства потока позволяют относить поток к классу пуассоновских; · овладеть способом определения характеристик потока с помощью формулы Пуассона. Успешно изучив тему, Вы: получите представление о: · постановке и примерах задач проверки гипотез; · критериях, применяемых при оценивании гипотез; · подходах к сбору исходных данных и анализу результатов моделирования в системах потоками заявок; будете знать: · как практически применить критерий проверки гипотезы к реальной задаче, возникающей при моделировании. Вопросы темы: 1. Постановка задачи проверки гипотез. 2. Пуассоновский поток. 3. Пример проверки гипотез. Вопрос 1. Постановка задачи проверки гипотез. Любое исследование системы методом моделирования основывается на использовании как количественных, так и качественных сведений относительно изучаемой системы. Одним из первых и наиболее важных этапов процесса моделирования является этап сбора исходных данных и приведение их к виду наиболее полно соответствующему требованиям удобства их последующего использования в модели. Например, исследование систем массового обслуживания, о которых будет идти речь далее, начинается с изучения того, что необходимо обслуживать, иначе говоря, с изучения характеристик входящего потока заявок. В нетривиальных случаях требуется также обследование самой системы массового обслуживания с целью нахождения характеристик обслуживания (потока обслуживания). Для каких-либо свойств или показателей системы часто приходится делать некоторое допущение относительно характера и параметров математической зависимости, описывающей значения показателя, основываясь на результатах наблюдения за значением показателя. После этого принятое допущение подвергается проверке. Решение этой задачи носит название проверки статистических гипотез. Существуют различные методы проверки статистических гипотез. Наиболее широко на практике используются критерии: · Пирсона, или (хи-квадрат). · Крамера-фон Мизеса. · Колмогорова-Смирнова. Критерий согласия предпочтителен в тех случаях, если объемы выборок (число значений, полученных или измеренных в результате наблюдений) N, в отношении которых проводится анализ, велики. Это мощное средство, если N > 100 значений. Следует, однако, заметить, что в ряде случаев, в частности, при анализе экономических ситуаций, бывает довольно трудно или невозможно найти 100 одинаковых процессов, развивающихся с различными исходными данными. Сложность заключается не только в том, что не бывает одинаковых объектов экономики, а и втом, что к исходным данным относятся не только исходные вероятностные данные и особенности структуры объекта. Влияние на процесс оказывает также сценарий развития процессов в этом объекте и в тех объектах внешней среды, с которыми он взаимодействует (процессы, протекающие на рынке, указы правительства, принятие новых законов, требования налоговых органов, платежи в бюджеты различных уровней). Критерий Крамера-фон Мизеса дает хорошие результаты при малых объемах выборок, обычно, для N < 10. Однако для N < 10 независимо от применяемого метода вопрос о доверительной вероятности при проверке статистической гипотезы решается плохо - эта вероятность мала при значительных размерах доверительных интервалов. Для выборок с объемами в пределах 10 < N < 100 согласно многим исследованиям хорошие результаты дает критерий Колмогорова-Смирнова. Он применяется в тех случаях, когда проверяемое распределение непрерывно и известны среднее значение и дисперсия испытуемой совокупности. Рассмотрим подробнее методику использования критерия на конкретном примере, предварительно познакомившись с часто встречающимся в моделях стохастических систем классом потоков, называемым пуассоновским. Вопрос 2. Пуассоновский поток. Поток требований называют однородным, если: · все требования потока обслуживаются в системе массового обслуживания одинаково; · рассмотрение требований (событий) потока, которые по своей природе могут быть различными, ограничивается рассмотрением моментов времени их поступления. Потокназывается регулярным, если события в потоке следуют один за другим через интервалы времени одинаковой длительности. Функция f(х) плотности распределения вероятности случайной величины Т, обозначающей интервал времени между событиями, для регулярного потока имеет вид: где - дельта функция; - математическое ожидание случайной величины T. Дисперсия интервала между событиями регулярного потока (моментами поступления требований) D[T] равна 0, а интенсивность наступления событий в потоке (среднее число требований в единицу времени) равна . Потокназывается случайным, если события в потоке следуют один за другим через интервалы времени случайной длительности. Случайный поток может быть описан как случайный вектор, который, в свою очередь, может быть задан одним из двух способов: 1) Функцией распределения моментов наступления событий где ti – значение моментов наступления Ti(i=1, n). 2) Функцией распределения интервалов между наступлением последовательных событий τ1, τ2, … τn: где i - значения интервалов между событиями τi(i=1, n). В последнем случае моменты наступления событий могут при необходимости быть найдены из рекуррентных соотношений: где t0 - момент наступления первого события потока. Поток называется стационарным, если вероятность попадания того или иного числа событий на элементарный участок времени длиной τ зависит только от длины участка и не зависит от того, где именно на оси t расположен этот участок. Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Поток событий называется ординарным, если вероятность попадания на элементарный участок двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Поток событий, обладающий всеми тремя указанными свойствами, называется простейшим, или стационарным пуассоновским потоком. Пуассоновский поток событий тесно связан с известным из теории вероятностей распределением Пуассона: число событий потока, попадающих на временной интервал некоторой величины, распределено по закону Пуассона. Если на временной оси t, где наблюдается поток событий, выделить некоторый участок времени длины τ, начинающийся в момент t0 и заканчивающийся в момент t0 + τ, то нетрудно доказать, что вероятность попадания на этот участок ровно m событий выражается формулой: 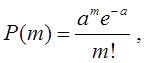 (1) (1)где а — среднее число событий, приходящееся на участок τ; е — основание натуральных логарифмов (2,71828 … ). 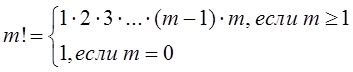 Для стационарного (простейшего) пуассоновского потока величина а равна интенсивности потока λ, умноженной на длину интервала: где интенсивность, или плотность потока λ есть среднее число событий, приходящихся на единичный временной интервал. В зависимости от физической природы изучаемой системы интенсивность может иметь различную размерность, например, чел/мин, руб/день, кг/час, запросов/сек, документов/сутки, отправлений/сутки и т.д. Функция распределения представляющая собой по определению вероятность того, что случайная величина Т (интервал времени между событиями) не превысит значения t, имеет для пуассоновского потока следующий вид: Такой закон распределения называется показательным (или экспоненциальным) с плотностью λ. Величина λ называется также параметром показательного закона. Математическое ожидание случайной величины равно: 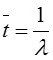 , (3) , (3)а дисперсия составляет: 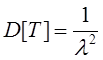 (4) (4)Среднеквадратическое отклонение случайной величины находится как квадратный корень из дисперсии: 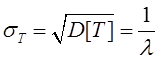 (5) (5)Как нетрудно видеть, математическое ожидание величины Т равно ее среднеквадратическому отклонению, что является характерной особенностью экспоненциального распределения. Таким образом, вероятность появления m событий в заданном промежутке времени описывается пуассоновским распределением, а вероятность того, что временные интервалы между событиями потока не превзойдут некоторого наперед заданного значения, описывается экспоненциальным распределением. Это различные описания одного и того же стохастического процесса. Вопрос 2. Пример проверки гипотез. Решение многих задач анализа и проектирования систем (в частности, систем массового обслуживания) намного упрощается в случаях, когда входящий поток и поток обслуживания являются простейшими (пуассоновскими). Покажем, каким образом можно вынести суждение о принадлежности наблюдаемого потока к пуассоновскому (напомним еще раз, что потоки этого типа имеют очень важное значение для решения практических задач, в чем вы сможете убедиться далее). Предположим, что проводилось наблюдение за потоком посетителей в отделении банка в течение 10 дней его работы. Результаты (число пришедших в течение часа в банк людей) представлены в таблице:
Определим интенсивность входящего потока покупателей за час работы отделения и, используя критерий Пирсона с уровнем значимости α=0,05, подвергнем проверке гипотезу о том, что поток описывается пуассоновским законом распределения. Сгруппируем данные по числу клиентов банка k, посетивших отделение в течение часа, а результаты представим в виде таблицы:
Предварительно заполнив в таблице для удобства вычислений дополнительную строку со значениями произведения
найдем величину интенсивности потока : 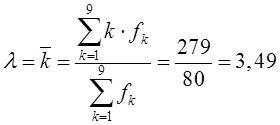 . .По формуле: 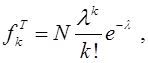 где 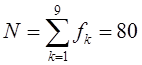 . .Находим и заносим в строку fТ теоретические значения частот:
Вычислим и занесем в строку таблицы: 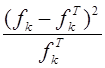 . .Значения, стоящие в числителе выражения под знаком суммы в формуле: 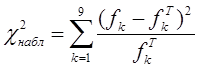 . .Для наблюдаемого значения критерия Пирсона:
В результате получаем наблюдаемое значение По заданному уровню значимости α=0,05 и числу степеней свободы: ν = n-2, где n - число групп в ряду (в нашем случае n=9) по таблице значений критических точек распределения находим Поскольку Вид теоретической и экспериментальной зависимостей для рассмотренного примера показан на диаграмме рис. 6: 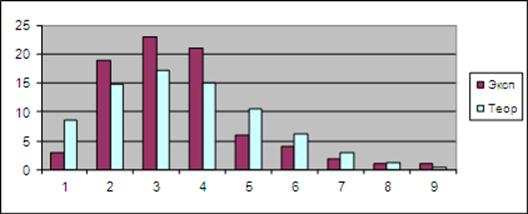 Рис. 6. Графики теоретической и экспериментальной зависимостей частот числа заявок входящего потока Предположим теперь, что проводилось наблюдение за временем обслуживания клиентов отделения банка кассиром, в результате чего получена таблица для частот интервалов следующего вида:
Определим среднее время и интенсивность μ обслуживания клиентов, после чего проверим на уровне значимости α=0,05 гипотезу о том, что время 1) Находим среднее значение каждого временного интервала по формуле: 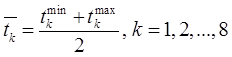 , ,Значения заносим в столбец, добавляемый к таблице справа:
2) Находим среднее время обслуживания 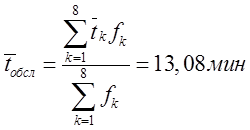 , ,и интенсивность μ обслуживания 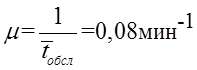 , ,Подсчитаем и занесем в ячейки отдельного столбца произведения
3) По формуле 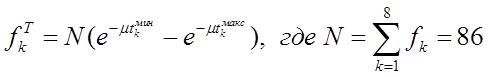 , ,находим теоретические частоты:
4) Вычислим и занесем в отдельный столбец таблицы значения 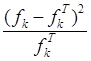 , входящие в выражение под знаком суммы в формуле , входящие в выражение под знаком суммы в формуле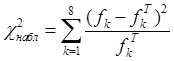 для наблюдаемого значения критерия Пирсона: для наблюдаемого значения критерия Пирсона:
Просуммировав, получим 5) По заданному уравнению значимости α=0,05 и числу степеней свободы ν = n–2 , где n – размер выборки (число групп в ряду, в нашем случае n=8) в таблице критических чисел находим 6) Поскольку Вид теоретической и экспериментальной зависимостей для рассмотренного примера показан на диаграмме: 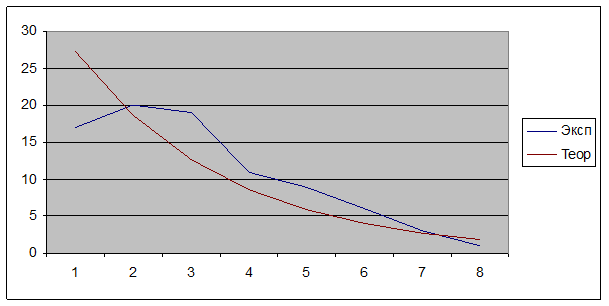 Рис. 7. Графики теоретической и экспериментальной зависимостей частот продолжительности обслуживания заявки Выводы: 1. Для эффективного решения задач на этапах сбора исходных данных для моделирования и анализа полученных результатов необходимо применять специальные методы. Одним из наиболее распространенных методов описания входных и выходных показателей является метод оценивания статистических гипотез. 2. Существуют несколько критериев, которые могут применяться для проверки гипотез. Выбор конкретного критерия зависит от условий, в которых производится оценивание гипотезы, в первую очередь, от объема выборки используемых для оценивания данных. 3. Для моделирования широкого класса систем и процессов необходимо строить математическое описание циркулирующих потоков объектов различного класса (информационных, материальных). Потоки могут характеризоваться различными свойствами, которые обусловливают тот или иной вид их математического описания. 4. Важным частным случаем потоков в моделируемых системах и процессах является пуассоновский поток. Поэтому в практических задачах целесообразно подвергать проверке гипотезу о принадлежности наблюдаемого потока к пуассоновскому, применяя тот или иной критерий. Вопросы для самопроверки: 1. В чем состоит сущность проверки статистических гипотез, и для каких задач моделирования она применяется? 2. Какие критерии проверки гипотез вы знаете? 3. От чего зависит выбор того или иного критерия проверки гипотез? 4. Что такое пуассоновский поток? 5. Как записывается и что позволяет найти формула Пуассона? 6. Как называется и что означает параметр пуассоновского закона? 7. Какому закону распределения подчиняются интервалы между поступлением отдельных заявок потока? 8. Как найти вероятность того, что в течение определенного интервала поступит не более определенного числа требований? 9. Чему равно математическое ожидание интервала времени между событиями в пуассоновском потоке? 10. Чему равно среднеквадратическое отклонение интервала времени между событиями в пуассоновском потоке? 11. Для чего нужно аппроксимировать экспериментальные данные относительно потока заявок и времени обслуживания в системе массового обслуживания теоретическими зависимостями? 12. Какие шаги нужно выполнить, чтобы построить теоретическую зависимость? 13. Зачем нужно проводить оценку статистической значимости результата? Литература по теме: 1. Бусленко Н.П. Моделирование сложных систем. – М.: Наука, 1968. – 356 с. 2. Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. – М.: Финансы и статистика, 2009. – 480 с. 3. Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. – М.: Финансы и статистика, 2009. – 848 с. |
