Математическое моделирование. Документ Microsoft Word. исследование и оптимизация свойств локальных информационных систем
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
|
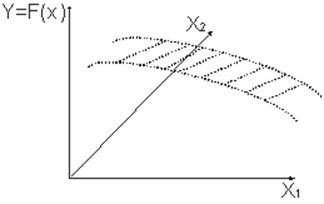
Тема 13. Планирование модельных экспериментов Цели изучения темы: · получить представление о задачах и методиках теории планирования эксперимента и ее приложениях к имитационному моделированию. Задачи изучения темы: · познакомиться с основными понятиями теории планирования эксперимента; · рассмотреть типовые постановки задач модельных экспериментов с точки зрения теории планирования эксперимента; · изучить подходы к решению основных задач. Успешно изучив тему, Вы: получите представление о: · области применения теории планирования эксперимента; · задачах, решаемых теорией планирования эксперимента; будете знать: · как правильно формулировать задачу к исследованиям на имитационных моделях и организовывать процесс экспериментов; · какими методами следует пользоваться для рациональной организации экспериментирования на имитационной модели; · как отбирать существенные факторы для экспериментов на модели. Вопросы темы: 1. Основы теории планирования эксперимента. 2. Отсеивающий эксперимент. 3. Аналитическое описание функции отклика. 4. Поиск оптимальных значений. Вопрос 1. Основы теории планирования эксперимента. Исследования, проводимые на имитационной модели, представляют собой частный случай научного эксперимента. Обычный подход к проведению экспериментов связан с большими временными и трудовыми затратами, поскольку сводится к последовательному варьированию отдельных совокупностей входных переменных при сохранении значений остальных неизменными, и измерению значений выходных переменных, получающихся для каждой совокупности значений входных переменных. Эксперименты на имитационной модели являются, как правило, многофакторными и связаны с поиском рациональной структуры и оптимизацией параметров моделируемой системы, отысканием оптимальных условий ее функционирования и т.д. Степень сложности исследуемой системы и, соответственно, используемой для исследований имитационной модели в очень многих случаях не позволяет провести ее всестороннее теоретическое изучение в разумные сроки. Поэтому, несмотря на значительный объем проведенных на модели экспериментов достаточно полный анализ объекта исследования оказывается невозможным и окончательное решение получается весьма приблизительным. Под экспериментом понимают совокупность операций, совершаемых над объектом исследования с целью получения информации о его свойствах. Если исследователь не может самостоятельно изменять условия его проведения, а лишь регистрирует их, то это случай пассивного эксперимента. Эксперимент, в котором исследователь по своему усмотрению может изменять условия его проведения, называется активным экспериментом. Объект, на котором возможен активный эксперимент, называется управляемым. Опытом называется отдельная часть эксперимента. Целью планирования эксперимента является нахождение таких условий и правил проведения опытов, при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности. Планирование эксперимента есть процесс выбора плана эксперимента, удовлетворяющего заданным требованиям, совокупность действий направленных на разработку стратегии экспериментирования (от получения априорной информации до получения работоспособной математической модели или определения оптимальных условий). Это целенаправленное управление экспериментом, реализуемое в условиях неполного знания механизма изучаемого явления. Результатом планирования эксперимента является план эксперимента, который представляет собой совокупность данных, определяющих число, условия и порядок проведения опытов. Проведение исследований на основе планирования эксперимента требует выполнения некоторых требований. Основными из них являются требования управляемости (см. выше) и воспроизводимости результатов эксперимента. Воспроизводимость характеризуется разбросом значений результата определенных опытов, проводимых через неравные промежутки времени: если разброс не превышает некоторой заданной величины, то объект исследования считается удовлетворяющим требованию воспроизводимости результатов. Хорошо составленный план эксперимента обеспечивает: · минимизацию общего число опытов; · одновременное варьирование всеми входными переменными; · использование математического аппарата, формализующего многие действия экспериментатора; · наличие четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов. Объект исследования в теории планирования эксперимента обычно представляется в виде «черного ящика» (рис. 55):  Рис. 55. Модель «черного ящика» Входы «черного ящика» (стрелки слева), обозначенные Х1, Х2,… Хn и представляющие собой воздействия на «черный ящик», называются факторами. Кроме того, на объект воздействуют возмущающие факторы, которые являются случайными и не поддаются управлению. Факторы, выбранные для эксперимента, должны отвечать требованиям: · однозначности; · независимости: факторы не должны оказывать влияния друг на друга; · совместимости: все комбинации факторов должны быть реализуемы и не приводить к абсурду; · управляемости: значение фактора можно задавать по усмотрению экспериментатора (предполагается активный эксперимент); · полноты: если какой-либо существенный фактор пропущен, это приведёт к неправильному определению оптимальных условий и появлению большой ошибки опыта. Факторы в эксперименте бывают количественными и качественными. Количественные факторы представляются в виде значения шкалы действительных чисел. Например, число обслуживающих приборов в системе массового обслуживания. Качественным факторам, значения которых не могут быть представлены числом, можно поставить в соответствие числовые обозначения, перейдя тем самым к количественным. Например, дисциплину обслуживания в обслуживающем приборе можно кодировать числами натурального ряда: «Первый пришел – первый обслужен»(FIFO) - 1, «Последний пришел – первый обслужен» (LIFO) - 2 и т.д. Для каждого из факторов указывают граничные значения. Диапазоны изменения факторов задают область определения Y. Если принять, что каждому фактору соответствует координатная ось, то полученное пространство называется факторным пространством. При n=2 область определения Y представляет собой прямоугольник, при n=3 – куб, при n >3 - гиперкуб. Факторы могут иметь разные размерности (Мбайт, ГГц, операций/с) и различные диапазоны изменения. В теории планирования эксперимента используют кодирование факторов. Переход к кодированным (безразмерным) значениям задается преобразованием 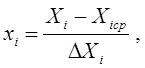 где Хi – натуральное (абсолютное) значение фактора; Хiср – именованное (абсолютное) значение фактора, соответствующее нулю в безразмерной шкале; DХi – интервал варьирования фактора; xi – кодированное значение фактора; Если фактор является качественным, то каждому уровню этого кодированного фактора присваиваются числа в диапазоне от +1 до –1. Так при двух уровнях это +1 и –1, при трех уровнях +1, 0, -1 и т.д. Совокупность основных уровней всех факторов представляет собой точку в пространстве параметров, называемую центральной точкой плана или центром эксперимента (Рис.). 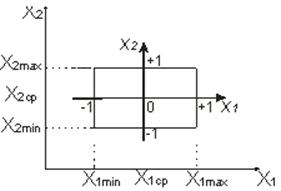 Рис. 53. Пространство параметров С геометрической точки зрения нормализация факторов равноценна линейному преобразованию пространства факторов, при котором проводятся две операции: 1) перенос начала координат в точку, соответствующую значениям основных уровней факторов в точку с координатами Х1сp, Х2сp … , Хnсp; 2) сжатие–растяжение пространства в направлении координатных осей таким образом, что минимальное значение кодированных факторов соответствует «-1», а максимальное значение «+1». Выходы «черного ящика называются откликом, а функция Y=F(Х1, Х2, …, Хn) – функцией отклика. Геометрическое представление функции отклика в факторном пространстве Х1, Х2, … , Хn называется поверхностью отклика (рис. 54):
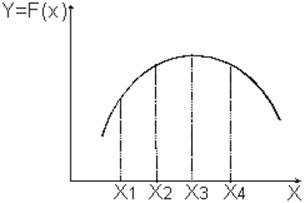
Если исследуется влияние на Y лишь одного фактора Х1, то нахождение функции отклика сложностей не вызывает. Задав несколько значений фактора, в результате опытов получаем соответствующие значения Y и график Y=F(X) (рис. ): Если факторов два, то необходимо провести опыты при разных соотношениях этих факторов. Функцию отклика в трехмерном пространстве можно графически представить в виде «контурной карты», которую можно считать видом сверху на трехмерную поверхность отклика, описывающую функцию Y (рис. 56 а), или же ее можно анализировать, проводя ряд сечений с фиксированными значениями второго (рис. 56,б) или первого факторов (рис. 56, в): 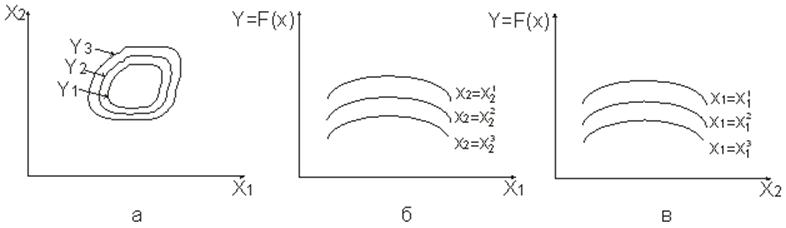 Рис. 56. Представление поверхности отклика двухфакторного эксперимента Если уверенности в том, что опыты хорошо воспроизводятся, нет, то опыты повторяют несколько раз и получают зависимость с учетом разброса опытных данных. По виду полученной функции отклика можно подобрать для нее математическое выражение. Подход к решению этой задачи рассмотрен в следующем вопросе темы. Вопрос 2. Отсеивающий эксперимент. Когда число факторов превышает семь, особую остроту приобретает задача выявления факторов, незначительно влияющих на показатель качества системы (функцию отклика). Планирование и проведение отсеивающего эксперимента позволяет выделить из всей совокупности факторов только наиболее существенные, подлежащие дальнейшему детальному изучению. Соответствующие планы применяют на начальных этапах исследования, когда нет конкретных сведений о влиянии тех или иных параметров. Отсеивание несущественных факторов снижает трудоемкость решения задач оптимизации или приближенного аналитического описания системы. При проведении отсеивающих экспериментов все факторы варьируются на двух уровнях. Нижний и верхний уровень каждого фактора выбираются из технологических соображений и предшествующего опыта. Общее число опытов должно быть не меньше числа исследуемых факторов. Комбинация уровней факторов определяется матрицей планирования - таблицей, показывающей, на каком уровне устанавливается каждый конкретный фактор в каждом опыте. В этой таблице «+1» (или просто «+») означает, что фактор берется на верхнем уровне, «-1» (или «-») - на нижнем. Для качественных факторов эти понятия условны, например, «дисциплина обслуживания» на нижнем уровне может быть LIFO, на верхнем – FIFO. Важно, чтобы отличие между уровнями было как можно больше в рамках допустимых пределов работоспособности исследуемой системы. В каждом конкретном опыте уровни факторов в отсеивающем эксперименте должны быть выбраны так, чтобы матрица планирования обладала следующими свойствами (свойства ортогональности): · сумма чисел в каждом столбце кроме первого равнялась нулю; · сумма произведений элементов, относящихся к одному опыту, для двух любых столбцов равнялась нулю. Примером матрицы планирования может быть следующая таблица (рис. 57):
Рис. 57. Пример матрицы планирования отсеивающего эксперимента Измерялась пропускная способность отделения банка в числе обслуженных клиентов в течение рабочего дня в зависимости от таких факторов как: 1 - день недели, 2 – качество помещения, 3 - район города, 4 - вид банковской операции, 5 - время (период) дня, 6 - категория клиента, 7 - квалификация кассира; Столбец с обозначением «0» не отвечает никакому фактору, он появился вследствие правила формирования матрицы, которое поясняется ниже. Собственно план эксперимента содержится в ячейках таблицы, заполненных символами серого цвета. Например, в опыте 5 первые три фактора берутся на верхнем уровне, а остальные четыре - на нижнем. Чтобы построить матрицу, обладающую свойствами ортогональности, за основу берутся так называемые матрицы Адамара. Матрица Адамара размерности 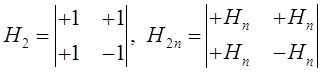 Матрица планирования в примере рис. 57 образована матрицей , отсюда столбец с номером 0. С такой матрицей можно проверить влияние не более семи факторов. Если их больше (от 8 до 15) , то следует строить матрицу . Число опытов в этом случае равно 16, если же факторов меньше 15, то просто отбрасываются последние столбцы матрицы . После выполнения эксперимента по данному плану анализируем его результат следующим образом. Для каждого фактора j,j=1,…7 находится сумма значений выходного параметра по всем опытам, где j-ый фактор был на верхнем уровне (+): 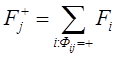 и сумму значений выходного параметра по всем опытам, где j-ый фактор был на нижнем уровне (-): 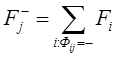 После чего находим разность и вносим результаты в соответствующие столбцы таблицы. Теперь ранжируем факторы по убыванию в предположении того, что более сильно влияющие факторы характеризуются большим значением абсолютной величины разности. Ранг фактора вносится в нижнюю строку таблицы. Это предположение, однако, нуждается в проверке, поскольку влияние может быть вызвано как случайным сочетанием уровней других факторов, так и тем, что максимальное влияние фактора проявляется не обязательно тогда, когда он находится на верхнем или нижнем уровнях, а тогда, когда он находится на каком-то промежуточном. Вопрос 33. Аналитическое описание функции отклика. Традиционные методики проведения экспериментов из-за зависимости компонентов восстанавливаемого аналитического описания не позволяют определить раздельное влияние каждого фактора на результирующий показатель, т. е. эти методики обеспечивают получение аналитических зависимостей, пригодных лишь для решения интерполяционных задач. В отличие от них теория планирования эксперимента дает возможность оценить вклад каждого параметра в значение показателя, т.е. приближенно восстановить закон функционирования объекта по экспериментальным данным. Полученное аналитическое описание объекта можно использовать для предварительного исследования вариантов построения системы или в интересах построения модели старшей системы, включающей данный объект на правах элемента. Эксперименты, направленные на раскрытие механизма исследуемого явления и определяющие аналитическую зависимость, называют интерполяционными или регрессионными. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||