Математическая модель морского волнения. реферат. " Математическая модель морского волнения "
 Скачать 95.16 Kb. Скачать 95.16 Kb.
|
|
Федеральное государственное бюджетное общеобразовательное учреждение высшего профессионального образования «КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Факультет судостроения и энергетики Кафедра Кораблестроения Реферат на тему: " Математическая модель морского волнения " Реферат выполнила студентка гр. 18 КС Москаленко Ю.В. Реферат проверил: д.т.н., доц. Дятченко С.В. Калининград 2022 г. Введение Волновым движением в жидкости называют процесс распространения в ней колебательного движения, а распространяющееся в жидкости периодическое возмущение — волной. Встречающиеся в природе волновые движения весьма разнообразны. К ним относятся: — ветровые волны, вызываемые и поддерживаемые ветром, действующим на свободную поверхность воды; — волны зыби, остающиеся после прекращения действия ветра или вышедшие из сферы его действия; — корабельные волны, создаваемые движением тел по свободной поверхности жидкости или вблизи нее; — внутренние волны, волны, возникающие в глубине морей и океанов в зоне с резким градиентом плотности, обусловленным изменением по вертикали температуры или солености; — морские волны прилива и отлива, вызываемые силами притяжения Луны и Солнца; —сейши, медленные колебания уровня воды, обусловленные неравномерным распределением атмосферного давления; — волны цунами, возникающие в результате подводных землетрясений; — капиллярные волны (так называемая рябь), возникающие под действием сил поверхностного натяжения. При рассмотрении движения корабля или подводных объектов вблизи границы раздела сред из всех перечисленных типов волн наибольшее значение имеют первые четыре. Для судостроительных расчетов важно знать свойства и количественные характеристики ветровых волн, волн зыби, корабельных волн и гравитационных внутренних воли. Это объясняется тем, что периоды остальных типов волновых движений — сейш, цунами, приливов и отливов и др. — во много раз больше периодов собственных колебаний судов и аппаратов, которые практически не реагируют на столь длиннопериодные возмущения. Нетрудно видеть, что приведенная классификация основана на различных причинах, поддерживающих процесс волнообразования. Так, первые четыре типа относятся к гравитационным волнам, ибо они существуют вследствие того, что жидкость находится в поле действия силы тяжести. Волны прилива и отлива существуют вследствие сил притяжения к Луне и Солнцу. Волны цунами в отличие от поверхностных волн охватывают всю массу жидкости, и их относят к разряду упругих волн. Капиллярные волны обусловлены действием сил поверхностного натяжения. Можно выделить четыре основных направления в изучении морских гравитационных волн: статистическое, спектральное, энергетическое и гидродинамическое. В работах статистического направления изучается разнообразие элементов ветровых волн. Многочисленные экспериментальные материалы, полученные с помощью измерений элементов волн (киносъемки, стереофотосъемки, записи колебаний уровня воды и т. д.), подвергаются массовой статистической обработке, анализируются и затем устанавливаются статистико-вероятностные закономерности элементов ветровых воли. Наиболее важными из них являются функции распределения элементов волн. При оценке мореходных качеств судов главным образом используются первые функции распределения. Оценивая степень важности работ статистического направления для расчета мореходности судов, следует признать, что статистика дает важные сведения о количественных характеристиках ветровых воли. Однако эти сведения непосредственно не связаны с гидромеханической сущностью процессов, которой обусловлено действие волнения на движущееся в море судно. Поэтому сама по себе статистика волн не вносит принципиально нового в оценку мореходности судов. Более эффективным в этом отношении является спектральное направление. По этому методу морское волнение рассматривается как сложный колебательный процесс — результат взаимодействия множества простых гармонических составляющих. Каждая из этих составляющих обладает кинематическими и динамическими свойствами прогрессивной волны малой амплитуды. Распределение энергии таких простых волн по спектральным частотам определяется энергетическим спектром. Зная результат воздействия на судно отдельной гармонической составляющей и спектральный состав волнения, можно найти спектр колебания судна. В многочисленных работах энергетического направления описывается процесс образования и развития волн под действием ветра. Составляется уравнение энергетического баланса движения воды и воздуха вблизи свободной поверхности. Решение этих уравнений корректируется по экспериментальным данным, и в результате получаются количественные зависимости характерных элементов волн в функции от скорости ветра и продолжительности его действия. Гидродинамическое направление основывается на математическом изучении волнового движения невязкой жидкости, имеющей свободную поверхность, или границу раздела сред, близких по плотности. К этим границам прикладывается импульс давления (порыв ветра или движение корабля). Гидродинамическая теория воли устанавливает количественные зависимости между отдельными элементами регулярной волны, дает формулы для ординат волнового профиля и давления внутри жидкости. С помощью гидродинамической теории волн можно рассчитать гидродинамические силы и моменты волновой природы, действующие на суда или аппараты. Эти силы и моменты могут существенно изменять гидродинамические характеристики тел по сравнению с таковыми при движении тел в неограниченной жидкости. В частности, к этим силам относится волновое сопротивление, имеющее большое значение с точки зрения ходкости судов [1]. Некоторые результаты классической гидродинамики волн Перед наблюдателем, смотрящим на взволнованную поверхность, проходят волны различных размеров. Однако в классической гидродинамике рассматривается одиночная волна. Полученные результаты основываются на решении уравнений движения идеальной жидкости при граничных и начальных условиях, обеспечивающих описание наиболее общих свойств волнового движения. Несмотря на идеализацию, принимаемую в классической гидродинамике, основные закономерности с достаточной степенью точности можно применить для реального волнения. Выражение для синусоидальной волны любой природы может быть записано двумя способами - в подвижной и неподвижной системах координат. Подвижная система координат О1yz связана c волной и движется вместе с ней. Расположим начало координат на уровне невозмущённой поверхности над подошвой волны. Ось z направим вертикально вниз, ось у -вправо. 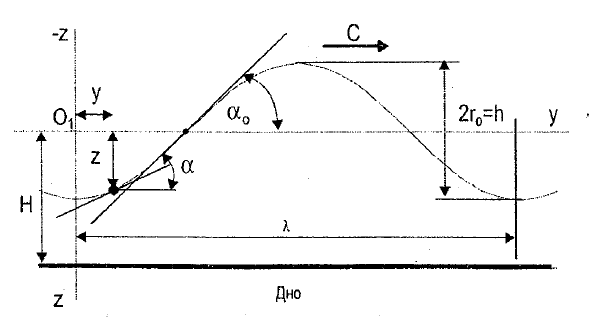 Рисунок 1.1 Основные элементы гармонической волны. Подвижная система координат  (1.1) На рис.1.1 рассмотрен пример гармонической двумерной синусоидальной волны, распространяющейся на акватории с глубиной Н. Тогда уравнение профиля волны будет (1.1): 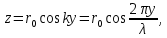  (1.2) где r0 - амплитуда; h=2r0 – высота волны; у – направление распространения волн; k=2/ - волновое число (частота формы). Угол волнового склона α (его тангенс) можно вычислить по формуле: 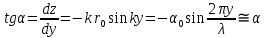 При малой высоте волны (по сравнению с длиной) можно считать, что тангенс угла волнового склона будет примерно равен самому углу (в радианах). Для многих практических задач удобнее записывать уравнение профиля волны в неподвижной системе координат Оζη. В начальный момент времени обо системы координат совпадают (рис. 1.2) 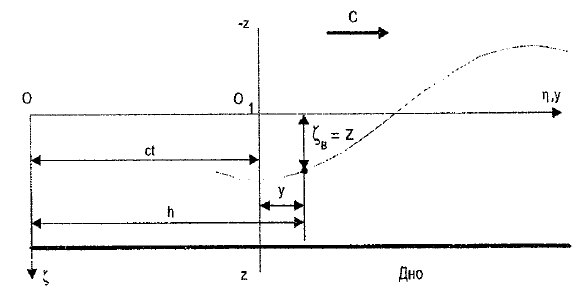 Рисунок 1.2 Основные элементы гармонической полны. Неподвижная система координат Через промежуток времениt подвижная система координат ‘убежит’ от неподвижной на расстояние ct (с – скорость волны). Тогда координаты той же точки будут 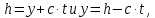 а 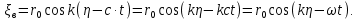 Выражение для утла волнового склона будет 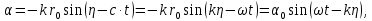 где α0 = kr0  (1.3) Если записать уравнение волны в начале координат (η= 0), то 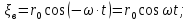 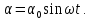 Если скорость волны с, то частота f, с которой будут мелькать гребни, равна f=c/. Круговая частота =2f. Перейдя от одного гребня к другому, мы сместимся на расстояние , а угол изменится на 2. Следовательно, выполняются соотношения k=2 или k=2/, а период =1/f, Таким образом, учитывая, что f=c/, имеем: c=/=f=/k . Если c=/k=const, то волна сохраняет форму (имеет место так называемая бездисперсная мода). Если с не постоянно, то волна при распространении меняет форму (дисперсная мода).  (1.4) Вид свободной поверхности остается неизменным по форме и перемещается с фазовой скоростью с: 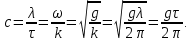 Траектории частиц представляют собой окружности радиуса 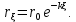  (1.5) 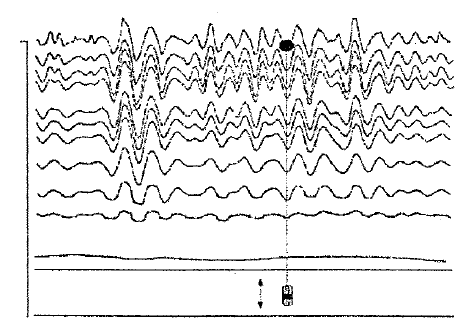 Рисунок 1.3 Схема измерения волнения с помощь поплавкового волнографа с гидростатическим датчиком На поверхности ζ=0, 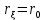 . При ζ=/2 . При ζ=/2 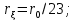 при ζ= при ζ= 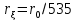 . Следовательно, волнение практически не проникает на глубины большие, чем длина волны. В результате прогрессивная волна не нарушает гидростатического давления на этой глубине. По этой причине гидростатические датчики всех поплавковых волнографов опускаются на глубину, большую длины волны и, несмотря на постоянное расстояние между поплавком и датчиком, возможно измерение волнения (рис 1.3). . Следовательно, волнение практически не проникает на глубины большие, чем длина волны. В результате прогрессивная волна не нарушает гидростатического давления на этой глубине. По этой причине гидростатические датчики всех поплавковых волнографов опускаются на глубину, большую длины волны и, несмотря на постоянное расстояние между поплавком и датчиком, возможно измерение волнения (рис 1.3).  (1.7) (1.6) Если глубина конечна (т.е. глубина моря сравнима с длиной волы), то амплитуда на свободной поверхности и частота волны зависят от глубина Н: 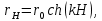 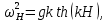   (1.9) (1.8) Здесь символами th и ch обозначены гиперболический тангенс и гиперболический котангенс. Период волны и скорость ее распространения равны: 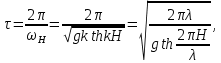 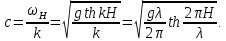 Орбиты, по которым движутся частицы на мелководье, становятся эллипсами (рис 1.4). 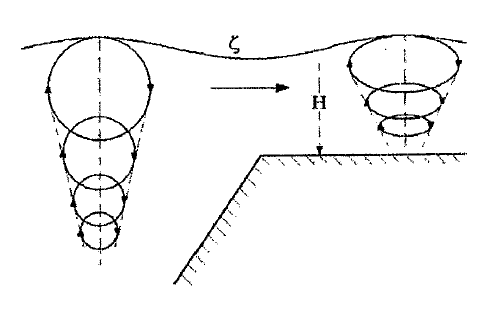 Рисунок 1.4 Траектория орбитальных движений жидких частиц в волне При большой глубине моря значение H/ велико и th(kH)=1, а выражение (1.9) сходится к соотношению (1.4).  (1.10) Если H/ мало, то th(kH)≈kH, тогда из (1.9) следует, что 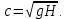 Эта формула Лагранжа, которая характеризует скорость распространения свободных длинных волн (например, приливных или цунами). Скорость распространения коротких гравитационных волн, как следует из (1.4), зависит от частоты или периода волны. Разнообразие волн в море обусловливает различную скорость их распространения. Даже в простейшем случае при распространении двух волн происходит их наложение, и образуются группы волн. Таков явление называют биениями. Групповая скорость сгр=df/dkможет быть также записана в виде: 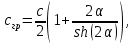 где α=2(Н/). У коротких (ветровых) волн сгр=с/2. У длинных волн sh(2α)=2α и поэтому групповая скорость примерно равна фазовой. В общем случае 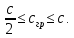 Ниже приведены значения отношения групповой и фазовой скоростей при различной относительной глубине водоема Н/. (табл. 1.1). Таблица 1 Соотношения между групповой и фазовой скоростями
В курсах гидродинамики также доказывается, что энергия волн распространяется с групповой скоростью. Следовательно, фронт возмущения распространяется с фазовой скоростью, но он несет малую энергию, а зона, где амплитуда заметна (внутри волнового пакета), распространяется с групповой скоростью. Приближение теории волн бесконечно малой амплитуды используется, когда амплитуда r0 волны мала по сравнению с ее длиной. Недостатки теории в данном случае связаны с тем, что волновое движение описывается как строго симметричное, с колебанием частиц по замкнутым орбитам. На малых глубинах деформация реальных волн существенно сложней, чем это определяется линейной теорией. В профиле мелководных волн появляется асимметрия, увеличивается волновое течение вследствие незамкнутости движения частиц по орбитам, которая в действительности имеет место. Для объяснения этих и других явлений разработана теория волн конечной амплитуды (нелинейная теория). Теория волн конечной амплитуды основана на следующих положениях: море глубокое; вода состоит из отдельных частиц, лишенных сил внутреннего трения; частицы описывают замкнутые круговые орбиты с одинаковыми радиусами в пределах одной и той же изобары; угловые скорости всех частиц одинаковы. Наиболее известна трохоидальная теория волн. Трохоида представляет след точки, нанесенной на любом расстоянии ζ от центра так называемого катящегося круга радиуса R [2]. Заключение Сложность физических процессов образования и распространения волн, многообразие факторов, от которых зависят характеристики волн, создают большие трудности в изучении морского волнения теоретическим путем и требуют его исследования в натурных условиях и с помощью модельных испытаний. В настоящее время еще не создано единой теории и общепризнанных методов расчета параметров морских волн, учитывающих в полной мере гидродинамические и физические факторы, которыми обусловливаются распространение, рост и затухание волны. Список использованных источников 1 А.Ш. Ачкинадзе, В.В. Васильева, Н.В. Корнев, Ю.И. Фаддеев. Гидромеханика: учебник для вузов/ Под общей редакцией проф. Н.В. Корнева и проф. Ю.И. Фаддеева.– СПб.: Мор Вест, 2007.-552с.,ил. 2 Маков Ю.Л. Качка судов: учеб.пособие/ Ю.Л.Маков.-Калининград: Изд-во ФГОУ ВПО ‘КГТУ’. 2007.-321 с. |
