Лекция. Лекция 12. Поверхности второго порядка

• Название: Лекция 12. Поверхности второго порядка
• Анкор: Лекция
• Дата: 08.04.2022
• Размер: 169.88 Kb.
• Имя файла: Lektsia_12_Poverkhnosti_2_poryadka_2021.docx
• Тип: Лекция; #452984
• страница: 1 из 6

Лекция 12. Поверхности второго порядка

1. 
   Цилиндрическиеповерхности.

Пусть  – цилиндрическая поверхность.

Выберем декартову СК так, чтобы ось 𝑂𝑧 была ^x

параллельна образующим. Кривая 𝛾 пересечения

поверхности Ф с плоскостью 𝑂𝑥𝑦 является направляющей. Пусть ее уравнение в плоскости 𝑂𝑥𝑦:



(в пространстве она задается системой из двух уравнений: 𝜙⁽𝑥, 𝑦⁾ = 0 и 𝑧 = 0).

Пусть 𝑀⁽𝑥, 𝑦, 𝑧⁾ – произвольная точка поверхности

. Тогда ее проекция на плоскость 𝑂𝑥𝑦 будет точка

𝑀₀⁽𝑥, 𝑦, 0⁾; и эта точка должна принадлежать кривой

𝛾. Поэтому ее координаты удовлетворяют (1). Но тогда этому уравнению будут удовлетворять и координаты точки 𝑀₀: координаты 𝑥 и 𝑦 у них одинаковы, а 𝑧 в уравнение не входит.

Обратно, пусть координаты точки 𝑀⁽𝑥, 𝑦, 𝑧⁾

удовлетворяют (1). Тогда этому же уравнению _x

удовлетворяют и координаты точки 𝑀₀⁽𝑥, 𝑦, 0⁾, а т.к.

𝑀₀ ∈ 𝑂𝑥𝑦, то 𝑀₀ ∈ 𝛾. При этом 𝑀 и 𝑀₀ лежат на одной прямой, параллельной оси 𝑂𝑧  M.

Итак, мы установили, что (1) и есть уравнение поверхности , т.е. уравнениецилиндрической поверхности совпадает с уравнением ее направляющей кривой  вплоскости 𝑂𝑥𝑦, если образующие параллельны оси 𝑂𝑧. Аналогично, если образующие параллельны 𝑂𝑦, то уравнение цилиндрической поверхности совпадает с уравнением направляющей кривой в плоскости 𝑂𝑥𝑧.

И обратно, если в уравнении поверхности отсутствует, например, координата x, то сразу можем сделать вывод, что эта поверхность цилиндрическая, а ее образующие параллельны 𝑂𝑥.

Пример.Пусть поверхность задана уравнением

𝑦² = 2𝑧. Тогда это цилиндрическая поверхность, ее образующие параллельны 𝑂𝑥, а направляющей служит парабола

_{𝑦² = 2𝑧,

𝑥 = 0.

Такая поверхность называется «параболическийцилиндр».

Поскольку уравнение цилиндрической поверхности совпадает с уравнением направляющей кривой, то список цилиндрических поверхностей

второго порядка совпадает со списком их направляющих кривых второго порядка.

Цилиндрические поверхности второго порядка

1. Эллиптический цилиндр	𝑥2 𝑦2 𝑎2 + 𝑏2 = 1
2. Мнимый эллиптический цилиндр ()	𝑥2 𝑦2 𝑎2 + 𝑏2 = −1
3. Гиперболический цилиндр	𝑥2 𝑦2 𝑎2 − 𝑏2 = 1
4. Параболический цилиндр	𝑦2 = 2𝑝𝑥
5. Пара пересекающихся плоскостей	𝑎2𝑥2 − 𝑏2𝑦2 = 0
6. Пара мнимых плоскостей, которые пересекаются по действительной прямой	𝑎2𝑥2 + 𝑏2𝑦2 = 0
7. Пара параллельных плоскостей	𝑥2 = 𝑎2
8. Пара совпадающих плоскостей	𝑥2 = 0
9. Пара мнимых параллельных плоскостей ()	𝑥2 = −𝑎2

y


z

y

_xy

2. 
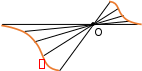   Коническиеповерхности.

Выберем ДСК так, чтобы начало координат совпадало с вершиной конической поверхности .

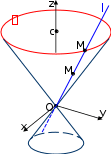Пусть 𝐹⁽𝑥, 𝑦, 𝑧⁾ = 0 – уравнение поверхности , где

𝐹 – многочлен второй степени от 3 переменных. Тогда функция двух переменных

𝜙⁽𝑥, 𝑦⁾ = 𝐹⁽𝑥, 𝑦, 𝑐⁾

будет многочленом второй степени для любого 𝑐 ∈ ℝ, а система

𝜙⁽𝑥, 𝑦⁾ = 0,

^{ 𝑧 = 𝑐

будет задавать сечение поверхности  плоскостью 𝑧 = 𝑐.

Получающуюся в сечении кривую 𝛾 выберем в качестве направляющей. Т.к. 𝜙⁽𝑥, 𝑦⁾ – многочлен 2 степени, то 𝛾 – кривая 2 порядка. Если 𝛾 – центральная, то можем считать, что ось Oz проходит через ее центр.

Предположим сначала, что направляющая – эллипс

_𝑥2 _𝑦2

_{𝛾: {𝑎2} + _𝑏2 − 1 = 0,

𝑧 = 𝑐.

(∗)

Пусть 𝑀(𝑥₁, 𝑦₁, 𝑧₁) – произвольная точка поверхности . Тогда вся прямая 𝑂𝑀

должна лежать на поверхности. Ее параметрические уравнения:

𝑥 = 𝑥₁𝑡,

_{𝑂𝑀: {}𝑦 = 𝑦₁𝑡,

𝑧 = 𝑧₁𝑡.

Пусть она пересекает направляющую 𝛾 в точке 𝑀₀(𝑥₀, 𝑦₀, 𝑐). Тогда ее координаты должны удовлетворять уравнению прямой 𝑂𝑀:

𝑥₀ = 𝑥₁𝑡,

_{𝑦₀ = 𝑦₁𝑡,

𝑐 = 𝑧₁𝑡,

𝑥₀ = 𝑥₁𝑐/𝑧₁,

⇒ {^{𝑦0 = 𝑦1𝑐/𝑧1,}

𝑡 = 𝑐/𝑧₁.

А теперь подставим найденные выражения в уравнение эллипса:

⁽𝑥₁𝑐/𝑧₁⁾²

_𝑎2 +

⁽𝑦₁𝑐/𝑧₁⁾²

_𝑏2 − 1 = 0.

Домножим это уравнение на




1

(
^𝑧 ) и получим

𝑐

_𝑥2

1 <sub>+

𝑎</sub>2

_𝑦2



1
_𝑏2

_𝑧2


1
− _𝑐2

= 0. (∗∗)

Обратно, пусть координаты точки 𝑀(𝑥₁, 𝑦₁, 𝑧₁) удовлетворяют уравнению (**).

Тогда этому уравнению удовлетворяют и координаты любой точки на прямой 𝑂𝑀:

⁽𝑥₁𝑡⁾²



_𝑎2

⁽𝑦₁𝑡⁾²

+ _𝑏2

⁽𝑧₁𝑡⁾²

− <sub>𝑐2

𝑥</sub> 2


₂ 1
= 𝑡 (

_𝑎2

_𝑦2


1
+ <sub>𝑏2

𝑧</sub>2

− ¹ ) = 𝑡² ⋅ 0 = 0

_𝑐2

а подставив в (2) 𝑧 = 𝑐, получим уравнение эллипса (_*). Значит, (2) и есть уравнение конической поверхности. Опуская индексы, окончательно получаем

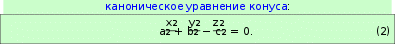
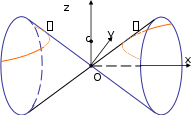Аналогично, если направляющая кривая – это гипербола

_𝑥2 _𝑦2

_{𝑎2 − _𝑏2 − 1 = 0,

𝑧 = 𝑐,

получим уравнение конической поверхности

_𝑥2

_𝑦2

_𝑧2

_𝑥2

_𝑦2

_𝑧2

_𝑎2 − _𝑏2 − _𝑐2 = 0 ⇔ − _𝑎2 + _𝑏2 + _𝑐2 = 0

Это такой же «эллиптический» конус, только ось его будет не 𝑂𝑧, а 𝑂𝑥.

Пусть теперь направляющая 𝛾 – это парабола

_{𝑥² = 2𝑝𝑦,

𝑧 = 𝑐.

Тогда тем же способом получим уравнение

𝑥² = ^2𝑝 𝑦𝑧. (∗∗)

𝑐

Повернем СК на 45° вокруг оси 𝑂𝑥.

Тогда формулы замены координат имеют вид

𝑥 = 𝑥^′,





𝑦 = ^{√2 (}𝑦^′ + 𝑧′⁾,


2

𝑧 = ^{√2 (}−𝑦^′ + 𝑧′⁾.

{

Подставим их в (



2

_**), и, обозначив
_𝑎2

= ^𝑝, получим

𝑐

𝑥² = 𝑎²(−𝑦^′2 + 𝑧^′2) ⇔ ^𝑥2 + 𝑦^′2 − 𝑧^′2 = 0.

_𝑎2

Таким образом, уравнение (_**) тоже определяет конус, ось которого является биссектрисой угла 𝑦𝑂𝑧.

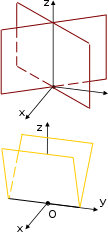Если направляющей служит пара прямых, то коническая поверхность представляет собой пару плоскостей, обязательно пересекающихся или совпадающих, т.к. обе плоскости должны проходить через начало координат. Эти поверхности относятся также к цилиндрическим, и они были рассмотрены в п.1.

y

3. 
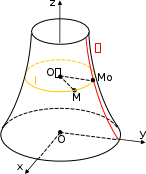
   Пусть некоторая кривая 𝛾 расположена в плоскости 𝑂𝑦𝑧. Будем вращать ее вокруг оси 𝑂𝑧. Получим некоторую поверхность , которая называется поверхностьювращения. Каждая точка кривой 𝛾 описывает окружность – параллель, центр которой лежит на оси 𝑂𝑧.
   
   Поверхностьвращения.

Пусть

𝜙⁽𝑦, 𝑧⁾ = 0 ⁽3⁾

– уравнение кривой 𝛾 в плоскости 𝑂𝑦𝑧. Тогда в пространстве она задается системой

_{𝜙⁽𝑦, 𝑧⁾ = 0,

𝑥 = 0.

Пусть 𝑀⁽𝑥, 𝑦, 𝑧⁾ – произвольная точка поверхности . Тогда она лежит на одной из таких

параллелей 𝑙 и может быть получена поворотом точки 𝑀₀⁽0, 𝑦₀, 𝑧₀⁾ = 𝛾 ∩ 𝑙. Очевидно, что

𝑧₀ = 𝑧 (∗)

и центр 𝑂′ параллели 𝑙 имеет координаты 𝑂′(0,0, 𝑧).

Кроме того, ^|𝑂′𝑀^| = ^|𝑂^′𝑀₀^| . В координатах это условие имеет вид





𝑦₀ = ^√𝑥² + 𝑦² (∗∗)


Координаты точки 𝑀₀ должны удовлетворять уравнению (3): 𝜙⁽𝑦₀, 𝑧₀⁾ = 0. Подставляя сюда (_*) и (_**), получаем

Обратно, пусть координаты точки 𝑀⁽𝑥, 𝑦, 𝑧⁾ удовлетворяют (4). Тогда, если выполнено (_*) и (_**), то этому уравнению будут удовлетворять координаты точки

𝑀₀⁽0, 𝑦₀, 𝑧₀⁾, а значит 𝑀₀ ∈ 𝛾. Кроме того, в силу (_*) и (_**) точка 𝑀₀ лежит на одной параллели с 𝑀, а значит 𝑀 может быть получена поворотом точки 𝑀₀ вокруг оси 𝑂𝑧


 𝑀 ∈ Φ.



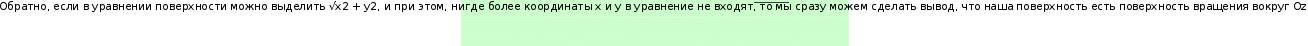
Пример1.Пусть 𝛾 – окружность в

плоскости 𝑂𝑦𝑧 радиуса 𝑏 с центром в ^z

точке 𝐴⁽0, 𝑎, 0⁾ ∈ 𝑂𝑦, 𝑎 > 𝑏. Будем вращать ее вокруг Oz. Получим поверхность, которая называется

^{тором. Уравнение окружности в} y

плоскости Oyzимеет вид:

⁽𝑦 − 𝑎⁾² + 𝑧² = 𝑏².

Вращаем вокруг 𝑂𝑧. Поэтому 𝑧 оставляем без изменений, а 𝑦 заменяем (𝑦 ↦ √𝑥² + 𝑦²):

(^√𝑥² + 𝑦² − 𝑎)2 + 𝑧² = 𝑏².

Получили уравнение тора. Заметим, что тор не относится к поверхностям 2 порядка.

Пример2.Поверхность  задается уравнением

𝑥² + 𝑧² = 2𝑦.

Мы можем переписать его так:

2

(^√𝑥² + 𝑧²) = 2𝑦.

Координаты 𝑥 и 𝑧 входят в уравнение только в выражении √𝑥² + 𝑧². Значит, наша поверхность – это поверхность вращения

вокруг 𝑂𝑦. Для того, чтобы получить

уравнение кривой, которая вращается, мы заменяем √𝑥² + 𝑧² на 𝑥 и получаем уравнение

кривой 𝛾 в плоскости 𝑂𝑥𝑦: 𝑥² = 2𝑦. В пространстве эта кривая задается системой

_{𝑥² = 2𝑦,

𝑧 = 0.

Точно так же мы можем заменить √𝑥² + 𝑧² на 𝑧 и получить уравнение кривой 𝛾′ в плоскости 𝑂𝑦𝑧: 𝑧² = 2𝑦. Вращая вокруг 𝑂𝑦 первую или вторую кривую, мы получим одну и ту же поверхность.