Лекция. Лекция 12. Поверхности второго порядка

• Название: Лекция 12. Поверхности второго порядка
• Анкор: Лекция
• Дата: 08.04.2022
• Размер: 169.88 Kb.
• Имя файла: Lektsia_12_Poverkhnosti_2_poryadka_2021.docx
• Тип: Лекция; #452984
• страница: 2 из 6

Эллипсоид.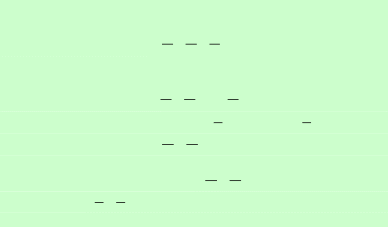

Определение.Эллипсоидомназывается поверхность , имеющая каноническое уравнение вида

_𝑥2 _𝑦2 _𝑧2

_𝑎2 + _𝑏2 + _𝑐2 = 1. (5)

Исследуем ее форму методомпараллельныхсечений. В сечениях плоскостями 𝑧 = ℎ получаем кривую

_𝑥2 _𝑦2 _ℎ2

_𝑎2 + _𝑏2 = 1 − _𝑐2 . (∗)

Если ^|ℎ^| ≠ 𝑐, то обозначим ⁽𝑎^′)2 = 𝑎² |1 − ^ℎ2|, ⁽𝑏^′)2 = 𝑏² |1 − ^ℎ2|.

_𝑐2 _𝑐2

_′2
При ^|ℎ^| < 𝑐 получаем эллипсы ^𝑥2

𝑎

_𝑦2


+
_𝑏′2

= 1, полуоси которых 𝑎^′ и 𝑏^′ достигают

максимального значения 𝑎 и 𝑏 при ℎ = 0.


_′2
При ^|ℎ^| > 𝑐 получаем мнимые эллипсы ^𝑥2

𝑎
_𝑦2


+
_𝑏′2
= −1 ⁽∅⁾. А при ℎ = ±𝑐 из (_*)

получаем уравнение ^𝑥2 + ^𝑦2 = 0, которое задает только одну из точек 𝐶

⁽0,0, 𝑐⁾ или

𝐶₂⁽0,0, −𝑐⁾.

_𝑎2

_𝑏2 1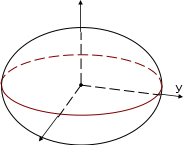

Аналогично, в сечениях плоскостями 𝑥 = ℎ (𝑦 = ℎ) в случае |ℎ| < 𝑎 (|ℎ| < 𝑏) получаем только эллипсы, полуоси которых достигают максимальных значений при ℎ = 0. При ℎ = ±𝑎 (ℎ = ±𝑏) будем получать одну точку. Прочиегеометрическиесвойстваэллипсоида. 1. Из уравнения (5) получаем, что |𝑥| ≤ 𝑎, |𝑦| ≤ 𝑏, |𝑧| ≤ 𝑐. Значит, весь эллипсоид
содержится в параллелепипеде, который определяется этими неравенствами.			z
2. Координатные оси пересекают		B1
эллипсоид в точках 𝐴1(𝑎, 0,0), 𝐴2(−𝑎, 0,0),
𝐵1(0, 𝑏, 0), 𝐵2(0, −𝑏, 0), 𝐶1(0,0, 𝑐),
𝐶2(0,0, −𝑐), которые называются вершинами
эллипсоида.		O
3. Координатные оси являются осями симметрии эллипсоида, координатные плоскости – плоскостями симметрии, начало		A1		C1
координат О– центром симметрии.	x

Действительно, пусть 𝑀⁽𝑥, 𝑦, 𝑧⁾ – произвольная точка эллипсоида. Тогда ее координаты ⁽𝑥, 𝑦, 𝑧⁾ удовлетворяют уравнению (5). Но тогда этому уравнению удовлетворяют также тройки чисел ⁽𝑥, −𝑦, −𝑧⁾, ⁽−𝑥, 𝑦, −𝑧⁾, ⁽−𝑥, −𝑦, 𝑧⁾, ⁽𝑥, 𝑦, −𝑧⁾, ⁽𝑥, −𝑦, 𝑧⁾, ⁽−𝑥, 𝑦, 𝑧⁾, ⁽−𝑥, −𝑦, −𝑧⁾, которые определяют точки симметричные 𝑀 соответственно относительно осей 𝑂𝑥,

𝑂𝑦, 𝑂𝑧, плоскостей 𝑂𝑥𝑦, 𝑂𝑥𝑧, 𝑂𝑦𝑧 и точки 𝑂. Поэтому все эти точки тоже принадлежат эллипсоиду.

M₂(x,y, z) ^z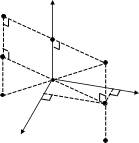


O

M_o(x,y,z)
x

M(x, y, z)
y

M₁(x, y, z)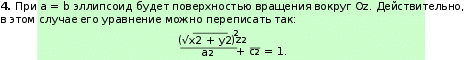

Аналогично, при 𝑎 = 𝑐 эллипсоид будет поверхностью вращения вокруг 𝑂𝑦, а при

𝑏 = 𝑐 – вокруг 𝑂𝑥.

При 𝑎 = 𝑏 = 𝑐 эллипсоид будет сферой:

𝑥² + 𝑦² + 𝑧² = 𝑎². (∗∗)

Произвольный эллипсоид может быть получен из сферы (_**) в результате равномерного сжатия (растяжения) по двум взаимно перпендикулярным


**
направлениям. Действительно, если в ( ) сделать замену координат 𝑥 = 𝑥′, 𝑦 = ^𝑎 𝑦′,

𝑏

𝑧 =

^𝑎 𝑧′, то получим уравнение (5), только со штрихами.

𝑐

5. Определение.Однополостнымидву поверхности, имеющие канонические уравн 𝑥2 𝑦2 𝑧2 Φ1 : 𝑎2 + 𝑏2 − 𝑐2 = 1 (6) В сечениях плоскостями 𝑧 = ℎ получае 𝑥2 𝑦2 ℎ2 𝑎2 + 𝑏2 = 1 + 𝑐2 Обозначим со 2 ℎ2 2 ℎ2 𝑎′ = 𝑎2 (1 + ) , 𝑏′ = 𝑏2 (1 + ) 𝑐2 𝑐2 при любом ℎ получаем эллипсы 𝑥2 𝑎′2 + 𝑏		полостнымгиперболоидаминазываются ения соответственно вида 𝑥2 𝑦2 𝑧2 Φ2 : 𝑎2 + 𝑏2 − 𝑐2 = −1 (7) м соответственно кривые 𝑥2 𝑦2 ℎ2 𝑎2 + 𝑏2 = −1 + 𝑐2 (∗) ответственно 2 ℎ2 2 ℎ2 𝑎′ = 𝑎2 |−1 + | , 𝑏′ = 𝑏2 |−1 + | 𝑐2 𝑐2 при |ℎ| > 𝑐 получаем эллипсы 2 ′2 = 1,
   полуоси которых 𝑎′ и 𝑏′ неограниченно возрастают при возрастании |ℎ|, и достигают минимумов 𝑎 и 𝑏 при ℎ = 0		полуоси которых 𝑎′ и 𝑏′ неограниченно возрастают при возрастании |ℎ|;

   
   
   
   Однополостныйидвуполостныйгиперболоиды.

𝑦

			при |ℎ| < 𝑐 получаем мнимые эллипсы 𝑥2 + 𝑦2 = 1 (∅), а при ℎ = ±𝑐 (*) 𝑎′2 𝑏′2 2 2 превращается в 𝑥 + 𝑦 = 0, которое 𝑎2 𝑏2 задает 𝐶1(0,0, 𝑐) или 𝐶2(0,0, −𝑐).
В сечениях плоскостями 𝑦 = ℎ получаем соответственно кривые 𝑥2 𝑧2 ℎ2 𝑥2 𝑧2 ℎ2 𝑎2 − 𝑐2 = 1 − 𝑏2 (∗∗) 𝑎2 − 𝑐2 = −1 − 𝑏2 Обозначим соответственно
2 ℎ2 2 ℎ2 𝑎′ = 𝑎2 |1 − | , 𝑐′ = 𝑐2 |1 − | 𝑏2 𝑏2 при ℎ ≠ ±𝑏 получаем гиперболы 𝑥2 𝑧2 𝑎′2 − 𝑐′2 = ±1, а при ℎ ≠ ±𝑏 (**) превращается в 2 2 уравнение 𝑥 − 𝑧 = 0, которое задает 𝑎2 𝑐2 пару пересекающихся прямых			2 ℎ2 2 ℎ2 𝑎′ = 𝑎2 (1 + ) , 𝑐′ = 𝑐2 (1 + ) 𝑏2 𝑏2 при любом ℎ получаем гиперболы 𝑥2 𝑧2 − + = 1. 𝑎′2 𝑐′2

Аналогично, в сечениях Φ₂ плоскостями 𝑦 = ℎ получаем только гиперболы, а в сечениях Φ₁ – гиперболы или пары прямых при ℎ = ±𝑎.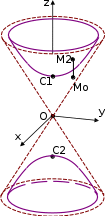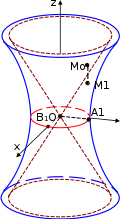

y

Прочиегеометрическиесвойствагиперболоидов.

1. 
   Из уравнения (7) получаем, что ^|𝑧^| ≥ 𝑐, т.е. в пространственном слое ^|𝑧^| < 𝑐 нет точек Φ_2. Координатные оси 𝑂𝑥 и 𝑂𝑦 пересекают Φ₁ в точках 𝐴₁⁽𝑎, 0,0⁾, 𝐴₂⁽−𝑎, 0,0⁾,
   

𝐵₁⁽0, 𝑏, 0⁾, 𝐵₂⁽0, −𝑏, 0⁾, которые называются его вершинами. Ось 𝑂𝑧 его не

пересекает.

Зато ось 𝑂𝑧 пересекает Φ₂ в точках 𝐶₁⁽0,0, 𝑐⁾, 𝐶₂⁽0,0, −𝑐⁾, которые называются его вершинами. Оси 𝑂𝑥 и 𝑂𝑦 не пересекают Φ₂.

2. 
   Точно так же, как и для эллипсоида доказывается, что координатные оси являются осями симметрии гиперболоидов, координатные плоскости – плоскостями симметрии, а точка 𝑂 – центром симметрии.
   
3. 
   При 𝑎 = 𝑏 гиперболоиды будут поверхностями вращения, а при 𝑎 = 𝑐 гиперболы в сечениях плоскостями 𝑦 = ℎ будут равнобокими. При 𝑏 = 𝑐 равнобокими будут гиперболы в сечениях плоскостями 𝑥 = ℎ.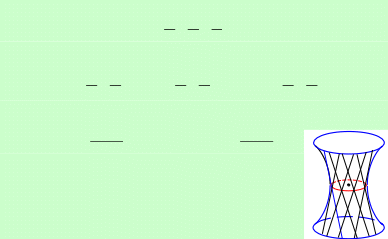
   
4. 
   Пусть Φ₀ – конус, заданный уравнением
   

_𝑥2 _𝑦2 _𝑧2

Φ₀ : _𝑎2 + _𝑏2 − _𝑐2 = 0.

Пусть 𝑀₀⁽𝑥, 𝑦, 𝑧₀⁾ ∈ Φ₀, 𝑀₁⁽𝑥, 𝑦, 𝑧₁⁾ ∈ Φ₁, 𝑀₂⁽𝑥, 𝑦, 𝑧₂⁾ ∈ Φ₂ – три точки с одинаковыми координатами 𝑥 и 𝑦, лежащие на конусе и на гиперболоидах. Тогда

_𝑥2

𝑧² = 𝑐² (

_𝑦2

+

_𝑥2

) , 𝑧² = 𝑐² (

_𝑦2

+

_𝑥2

− 1) , 𝑧² = 𝑐² (

_𝑦2

+

+ 1),

0 <sub>𝑎2

𝑏2</sub> 1

_𝑎2

_𝑏2

2 <sub>𝑎2

𝑏</sub>2

⇒ ^|𝑧^2| < ^|𝑧^2| < ^|𝑧^2|, а значит, Φ₁ лежит снаружи конуса Φ₀, а Φ₂ – внутри. Кроме

1 0 2

того, из тех же равенств следует 𝑧² − 𝑧² = 𝑧² − 𝑧² = 𝑐² ⇒

0 1 2 0

1 1

𝑀₀𝑀₁ = ^|𝑧₀ − 𝑧₁^| = <sub>|𝑧

+ 𝑧 |</sub> → 0, 𝑀₂𝑀₀ = ^|𝑧₂ − 𝑧₀^| = _|𝑧

+ 𝑧

_| → 0,

0 1 2 0

когда точки 𝑀₀, 𝑀₁, 𝑀₂ уходят на бесконечность (необходимо при этом заметить, что 𝑧₀, 𝑧₁ и 𝑧₂ все стремятся к бесконечности при

𝑥 → ∞ или 𝑦 → ∞). Значит, оба гиперболоида асимптотически приближаются к конусу.

5. 
   Φ₁ является линейчатой поверхностью и через каждую его точку проходит пара прямых, лежащая на поверхности.