Лекция. Лекция 12. Поверхности второго порядка
 Скачать 169.88 Kb.
|
Решение.Пусть M(x, y) – произвольная точка поверхности. Тогда | MF| = (x– a)2 + y2+z2,а расстояние от M до плоскости равно | x+ a|. По условию 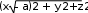 = | x+ a|.Возводим это равенство в квадрат: x2 – 2ax + a2 + y2+z2 = x2 + 2ax + a2 y2+z2 = 4ax y2  2a+ z2  2a= 2ax.Это уравнение задает эллиптический параболоид, осью которого является Ox. x2 y2 z2 x–1 y–4   Найдитеточкипересеченияэллипсоида= z+ 6 . 12 9 + 36 + 81 = 1 ипрямой 1 = – 6 Решение.Перепишем уравнение прямой в параметрическом виде: 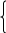 x = 1 + t, y= 4 – 6t,z= – 6 + 12t. Подставим эти равенства в уравнение эллипсоида: (1 + t )2  9 +4(2 – 3t)2  36 +9(–2 + 4t)2  81 = 1,1 + 2t+ t2 + 4 –12t+ 9t2 + 4 – 16t+ 16t2 = 9, 26t2 – 26t= 0 26t(t– 1) = 0. Имеем два решения: t1= 0, t2= 1. Подставляя их в уравнение прямой, находим две точки M1(1, 4,– 6), M2(2, –2, 6). Ответ: M1(1, 4,– 6), M2(2, –2, 6). x2 y2 – z2  Определить,какаякриваяполучаетсявсеченииповерхностиплоскостьюа) y= 2z; б) y= 2z+2. 9 + 16 4 = 1 Решение.а) Данная поверхность – это однополостный гиперболоид. Подставим y= 2zв уравнение поверхности: x2 (2z)2 – z2 2  9 + 164 = 1 x = 9. Это уравнение проекции данной кривой на координатную плоскость Oxz. Оно задает пару параллельных прямых. Следовательно, наша кривая – это тоже пара параллельных прямых.  б) Подставим y= 2z+4 в уравнение поверхности:x2 (2z+2)2 – z2 x2 z2 +4z+4 – z2 2  9 + 164 = 1 9 + 4 = 1 x = 9z. Это уравнение проекции данной кривой на координатную плоскость Oxz. Оно задает параболу. Следовательно, наша кривая – это тоже парабола. |