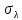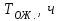Основы научных исследований и инновационной деятельности. курсовая работа. N 1 4 1 3 число степеней свободы. 23
 Скачать 2.99 Mb. Скачать 2.99 Mb.
|
1 2 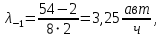 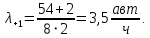 Интенсивность обслуживания – среднее число обслуженных автомобилей в единицу времени. 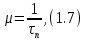  Потоки обслуживания и поступления носят вероятностный характер, как правило, описываемый нормальным законом распределения с коэффициентом вариации υ = 0,1…0,33. Принимаем: υ𝛌 = 0,2, υμ=0,2. Для них рассчитаем среднеквадратическое отклонение:  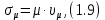   Далее строится матрица спектра плана. Для получения 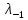 и и  изменим суточную программу соответственно 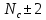 . .Для получения значений 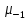 и и 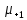 изменим число рабочих, изменим число рабочих, одновременно работающих на посту (соответственно 1 и 3 человека). 1.5 Установления основного содержания модели Зона ТР относится к системе массового обслуживания. Работа системы массового обслуживания заключается в следующем. В данную систему в случайный момент времени поступают заявки на обслуживание, они оформляются в контрольно-техническом пункте (КТП). Далее автомобиль поступает в зону ТР, где проводятся следующие работы: – контрольные работы: контроль технического состояния деталей, аппаратов, узлов и агрегатов, обеспечивающих работоспособность подвижного состава, безопасность дорожного движения, электро- и пожаробезопасность, контроль подвижного состава в целом; – уборочно-моечные работы; – смазочные, очистительные и заправочные работы. После прохождения зоны ЕО автомобиль поступает в зону Д, где проводится диагностирование либо отдельных узлов и агрегатов, либо технического состояния автомобиля в целом, после чего автомобиль направляется в зону ТО-1 либо в зону ожидания если пост ТО-1 занят, после освобождения поста ТО-1 на него поступает автомобиль. Далее автомобиль передается в зону хранения, откуда передается заказчику через КТП. Схема движения автомобиля в зоне ТР представлена на рисунке 1.1.  Рисунок 1.1 – Схема движения автомобиля в зоне ТР 1.6 Обоснование критериев моделирования и проверка достоверности концептуальной модели Зону ТР ОАС относим к системе массового обслуживания. Работа системы массового обслуживания заключается в следующем. В данную систему в случайный момент времени поступают заявки на обслуживание, которое осуществляется на соответствующих постах, после чего заявки покидают систему. Работа системы массового обслуживания характеризуется: пропускной способностью, то есть числом поступивших и обслуженных заявок средним числом заявок в очереди, средним временем ожидания в очереди, средним временем пребывания в системе. В качестве критериев моделирования принимаем абсолютную пропускную способность, среднее время ожидания в очереди, относительная пропускная способность. Среднее время нахождения в системе – критерий, характеризуемый средним временем пребывания автомобиля в системе за определённый промежуток времени. Среднее время ожидания в очереди – критерий, характеризуемый средним временем пребывания автомобилей в очереди за определённый промежуток времени. Абсолютная пропускная способность характеризуется средним числом заявок, которую может обслужить система массового обслуживания в единицу времени. Относительная пропускная способность – отношение числа обслуженных заявок к количеству заявок поступивших в систему. Вероятность обслуживания характеризуется законом распределения, который характеризуется коэффициентом вариации. Также систему массового обслуживания характеризуют: среднее число заявок в очереди, среднее число заявок в системе, среднее время ожидания в очереди, среднее время пребывания в системе. Эти критерии характеризуют эффективность работы системы. Критерии моделирования: число постов, число рабочих на посту, время работы зоны ТР, суточное поступление автомобилей, трудоемкость одного воздействия, дни работы в году, интенсивность поступления автомобилей в зону ТР, интенсивность обслуживания. Критерии моделирования должны иметь экономические и технико-экономические показатели. Критерии отвечающие экономическим и технико-экономическим показателям приведены в таблице 1.4. Таблица 1.4 – Значимые критерии моделирования
С помощью этих критериев решаются задачи оптимизации работы зоны ТР, позволяют смоделировать зону и получить показатели ее работы. Эти критерии характеризуют эффективность работы системы. 2 Алгоритмизация модели системы 2.1 Построение логической схемы работы зоны ТР 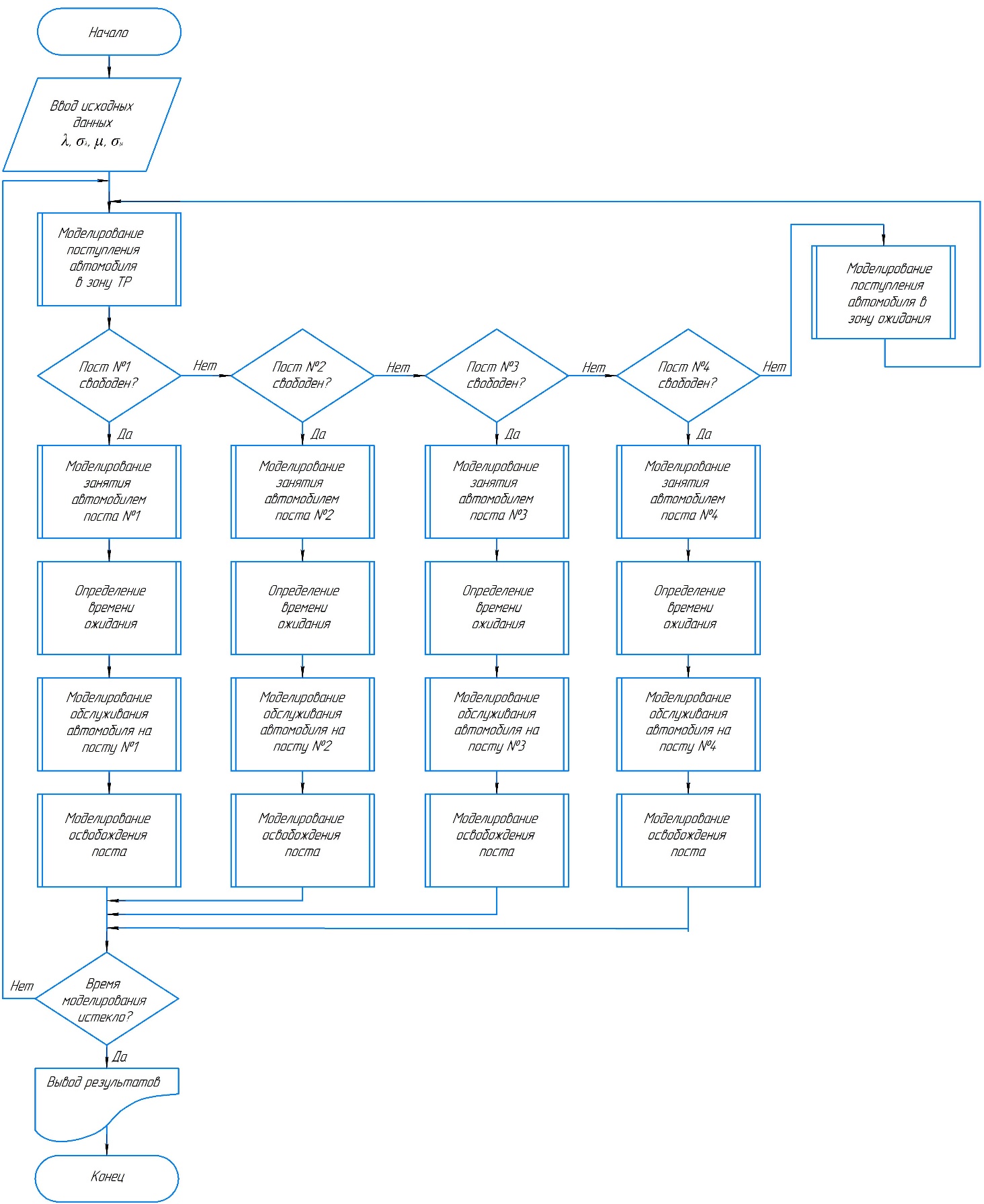 Рисунок 2.1 – Схема алгоритма моделирования работы зоны ТР 2.2 Получение математических соотношений для описания функционирования системы Из анализа уравнения Эрланга для систем массового обслуживания с ожиданием при установившемся режиме работы, вероятности нахождения системы в состоянии:   , при а ≤ к ≤ n , при а ≤ к ≤ n(2.1) 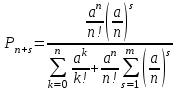 при 1 ≤ s ≤ m при 1 ≤ s ≤ mгде 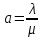 - новая переменная. - новая переменная.Уравнения (2.2) получают путём анализа уравнения Эрланга, при котором определяется закономерность поведения вероятностей. Вероятность отказа в обслуживании наступит при занятии всех постов и всех мест в очереди. 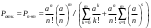 (2.2) (2.2)Вероятность обслуживания будет равна:  (2.3) (2.3)Относительная пропускная способность будет равна: 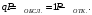 (2.4) (2.4) (2.5) (2.5)2.3 Выбор вычислительных средств для моделирования Решение поставленной задачи обеспечивает персональный компьютер, оснащённый процессором AMD Intel i5 c установленной памятью 8,00 ГБ, 64-разрядной операционной системой, операционной системой Windows 10, монитором VGA. В связи с использованием процессора с высокой тактовой частотой используем модулятор DOSbox. Вводим команды: mount с: с:\sim с: simsim После чего модулятор DOSbox запускает программу simsim и проводим серию экспериментов. 3 Регрессионный анализ работы системы 3.1 Результаты вычислительного эксперимента Регрессионный анализ необходим для получения математических соотношений между используемыми в модели параметрами или факторами и показателями эффективности работы системы. Необходимое число опытов N для полно-факторного эксперимента.  (3.1) (3.1) где V – число уровней варьирования, V = 2; n – число значимых факторов, n = 2 За число учитываемых факторов целесообразно принять такие комплексные факторы как средняя интенсивность поступления автомобилей λ и среднюю интенсивность обслуживания автомобилей μ. Составленная матрица спектра плана приведена в таблице 3.1. Таблица 3.1 – Матрица спектра плана
Построим матрицу спектра плана. Для получения 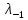 и и  изменим суточную программу соответственно изменим суточную программу соответственно 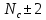 . .Для получения значений 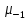 и и 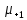 изменим число рабочих, одновременно работающих на посту (соответственно 1 и 3 человека). изменим число рабочих, одновременно работающих на посту (соответственно 1 и 3 человека).Результаты расчёта сведём в таблицу 3.2. Таблица 3.2 – Результат расчёта
В соответствии с матрицей спектра плана проводим эксперимент с использованием программы «simsim.exe». Накопители, используемые в модели, не ограничиваем по ёмкости и времени ожидания. В качестве основных критериев эффективности, принимаем среднее время нахождения в системе, среднее число занятых каналов, среднее время ожидания в очереди. Результаты эксперимента представим в таблице 3.3. При этом время моделирования Тм рассчитывалось по формуле:  (3.2) (3.2)Tмод = 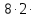 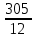 = 407 ч. = 407 ч.В результате проведения опыта получили некоторые значения функции отклика. Представим их в таблице 3.3. Таблица 3.3 – Матрица спектра плана и функции отклика для каждого опыта
Результаты эксперимента представим в таблице 3.4. Таблица 3.4 – Результаты эксперимента
Окончание таблицы 3.4
3.2 Оценка значимости коэффициентов уравнения регрессии Общий вид уравнения регрессии: 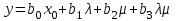 (3.3) (3.3)где b0, b1, b2, b3 - коэффициенты линейного уравнения регрессии. Определение коэффициентов уравнения регрессии осуществляется по матричному уравнению: 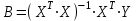 (3.4) (3.4)где Х матрица спектра плана; ХТ транспонированная матрица спектра плана; Y матрица результатов эксперимента. Таким образом, последовательно перемножая обратную матрицу (ХТ Х)-1 на транспонированную матрицу ХТ и на матрицу результатов Y, можно определить значения коэффициентов b0,b1,…,bj,…,bn. Для нахождения среднего числа занятости каналов коэффициенты регрессии будут равны:
Для нахождения среднего числа заявок в системе коэффициенты регрессии будут равны:
Для определения значимости коэффициентов уравнения регрессии необходимо их сравнить с половиной доверительного интервала  . Коэффициенты уравнения регрессии значимы, если половина доверительного интервала разброса коэффициентов . Коэффициенты уравнения регрессии значимы, если половина доверительного интервала разброса коэффициентов  ≤ bj. Если это условие не выполняется, то коэффициент незначим. Стоящий при нём фактор не оказывает влияния на критерий эффективности и его можно исключить из уравнения регрессии. ≤ bj. Если это условие не выполняется, то коэффициент незначим. Стоящий при нём фактор не оказывает влияния на критерий эффективности и его можно исключить из уравнения регрессии. (3.5) (3.5)где Sbj – среднеквадратическое отклонение коэффициента; t(α;k2) – критерий Стьюдента; α – уровень значимости, α = 0,05; k2 – число степеней свободы, k2 = 2; tα(0,05;2) = 4,3 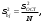 (3.6) (3.6)где Sост. - остаточная дисперсия  (3.7) (3.7)где yiр - рассчитанное по уравнению регрессии значение критерия эффективности в i-ой точке спектра плана. Расчётные значения для среднего числа занятости каналов: 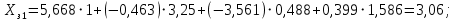 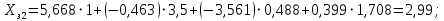 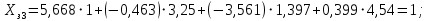  Расчётные значения для среднего числа заявок в системе:    ; ; . .По формуле (3.7) определим остаточную дисперсию. Для среднего числа занятости каналов остаточная дисперсия будет равна: 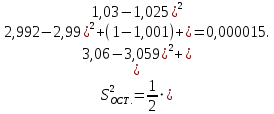 Для среднего числа заявок в системе остаточная дисперсия будет равна: 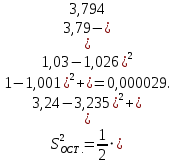 По формуле (3.6) определим квадрат среднеквадратического отклонения коэффициента. Для среднего числа занятости каналов Sbj2 равно:  Для среднего числа заявок в системе Sbj2 равно:  По формуле (3.5) определим половину доверительного интервала δ. Для абсолютной пропускной способности δ равна: 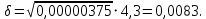 Для числа обслуженных автомобилей δ равна:  Сравним коэффициенты первого уравнения регрессии с половиной доверительного интервала: 5,668 >  ; |-0,463| > ; |-0,463| >  ; |-3,561| > ; |-3,561| >  ; ;0,399 >  . Отсюда следует, что коэффициенты b0, b1, b2, b3 значимы. . Отсюда следует, что коэффициенты b0, b1, b2, b3 значимы.Уравнение регрессии для среднего числа занятости каналов принимает вид: 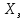 = 5,668-0,463·λ-3,561·µ+0,399·λ·µ. = 5,668-0,463·λ-3,561·µ+0,399·λ·µ.Сравним коэффициенты второго уравнения регрессии с половиной доверительного интервала: 16,622 > 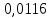 ; |-3,486| > ; |-3,486| > 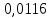 ; ; |-11,396| > 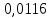 ; 2,561 > ; 2,561 > 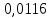 . .Отсюда следует, что коэффициенты b0, b1, b2, b3 значимы. Уравнение регрессии для среднего числа заявок в системе имеет вид: Хс = 16,622-3,486·λ-11,396·µ+2,561·λ·µ. 3.3 Оценка адекватности математической модели Уравнение регрессии должно адекватно описывать поведение реальной системы. Степень адекватности, соответственно, точность регрессионной модели оценивается с помощью критерия Фишера. Если опытный критерий Fоп ≥ Fт табличному критерию, то модель адекватна и наоборот. FT(α;k1;k2) ≤ Fоп, (3.8) где К1 = N – 1 = 4 – 1 = 3 – число степеней свободы. FT(0,05;3;2)=19,3.  (3.9) (3.9)где Sy2 – дисперсия среднего: 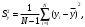 (3.10) (3.10)где  - среднее значение функции отклика - среднее значение функции отклика (3.11) (3.11)Для среднего числа занятости каналов способности  равно: равно: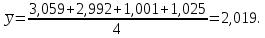 Для среднего числа заявок в системе  равно: равно: По формуле (3.10) определим дисперсию воспроизводимости. Для среднего числа занятости каналов  равно: равно: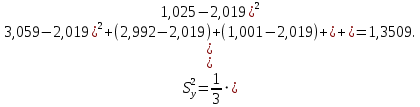 Для среднего числа заявок в системе  равно: равно: По формуле (3.9) определим опытное значение критерия Фишера. Для среднего числа занятости каналов 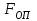 равно: равно: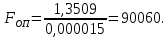 Для среднего числа заявок в системе 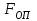 равно: равно: Сравним опытное и табличное значения критерия Фишера соответственно для среднего числа занятости каналов, среднего числа заявок в системе.   Обе модели адекватны. т.к. модель адекватна, то, анализируя уравнение регрессии, получим лучшие значения и , соответствующие оптимальному значению критерия эффективности. Для среднего числа занятости каналов: 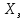 = 5,668-0,463·λ-3,561·µ+0,399·λ·µ. = 5,668-0,463·λ-3,561·µ+0,399·λ·µ. . . Процесс определения области экстремума сведем в таблицу 3.5: Таблица 3.5 – Процесс определения области экстремума
Получаем оптимальные значения интенсивности поступления и обслуживания для среднего числа занятости каналов: 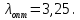 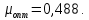 Для среднего числа заявок в системе: Хс = 16,622-3,486·λ-11,396·µ+2,561·λ·µ.  . . Процесс определения области экстремума сведем в таблицу 3.6: Таблица 3.6 – Процесс определения области экстремума
Получаем оптимальные значения интенсивности поступления и обслуживания для среднего числа заявок в системе: 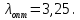  . .4 Оптимизации производственного процесса зоны Используемая в настоящее время методика определения числа постов в производственных зонах не позволяет выбирать их оптимальное количество. Для решения этой задачи необходимо использовать имитационные модели производственных подразделений. Для оптимизации производственного процесса необходимо вычислить суммарные затраты, связанные с ним. При этом расчёты проведём для различного числа обслуживаемых каналов для того, чтобы после сравнения затрат выбрать оптимальное число каналов на участке.  (4.1) (4.1)где  - суммарные затраты; - суммарные затраты; - затраты, связанные с простоем автомобиля; - затраты, связанные с простоем автомобиля; - затраты на содержание производственного участка; - затраты на содержание производственного участка;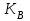 - капитальные вложения в создание производственного участка; - капитальные вложения в создание производственного участка; - число обслуживаний за период моделирования; - число обслуживаний за период моделирования; - нормативный коэффициент капвложений, - нормативный коэффициент капвложений,  Проведём моделирование системы на компьютере для 1,2,3,4,5 постов. Результаты моделирования представим в таблице 4.1. Таблица 4.1 – Значения, полученные в ходе моделирования для выбранного числа постов
Имея эти значения найдём затраты, связанные с простоем автомобиля:  (4.2) (4.2)где  – плата за 1 час использования автомобиля, – плата за 1 час использования автомобиля,      Эксплуатационные затраты на содержание производственного участка: 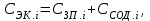 (4.3) (4.3)где  - зарплата ремонтных рабочих; - зарплата ремонтных рабочих; - затраты на содержание рабочих постов. - затраты на содержание рабочих постов.Затраты на зарплату ремонтных рабочих:  (4.4) (4.4)где Р – число рабочих на одном посту, Рп=2;  - моделируемое число постов; - моделируемое число постов;S – часовая тарифная ставка рабочего, S=0,4 у.е.; 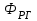 - годовой фонд времени рабочего, - годовой фонд времени рабочего,   - коэффициент доплат, - коэффициент доплат,  с – коэффициент сменности, с = 2. По формуле (4.4) рассчитаем  : :     Затраты на содержание рабочих постов:  (4.5) (4.5)где 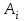 - амортизационные отчисления на ремонт и замену оборудования; - амортизационные отчисления на ремонт и замену оборудования; - эксплуатационные затраты на электроэнергию, воду, сжатый воздух и т.д. - эксплуатационные затраты на электроэнергию, воду, сжатый воздух и т.д. (4.6) (4.6)где  - стоимость оборудования одного поста, - стоимость оборудования одного поста, 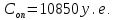  - коэффициент амортизационных отчислений, - коэффициент амортизационных отчислений,  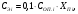 (4.7) (4.7)По формуле (4.7) определим  : :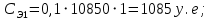  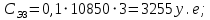   По формуле (4.6) определим 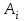 : : ; ; ; ;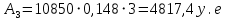 ; ; ; ; . .По формуле (4.5) определим  : :  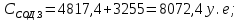  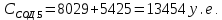 По формуле (4.3) определим  : :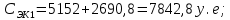  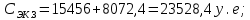   Капитальные затраты определяются суммой стоимостей приобретения и монтажа оборудования, а также стоимость строительства производственного участка  . . 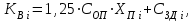 (4.8) (4.8)где  - стоимость зданий, сооружений при определённом числе постов. - стоимость зданий, сооружений при определённом числе постов.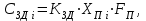 (4.9) (4.9)где 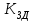 - стоимость строительства 1м2 производственного участка, - стоимость строительства 1м2 производственного участка, 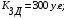  - площадь одного рабочего поста. - площадь одного рабочего поста.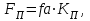 (4.10) (4.10)где fa – площадь автомобиля Honda Civic в плане, fa = 4,39  = 7,419 = 7,419   - коэффициент плотности расстановки, - коэффициент плотности расстановки,  . .По формуле (4.10) определим  : : = 7,419 = 7,419 4 = 29,676 4 = 29,676 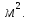 По формуле (4.9) определим  : :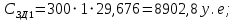 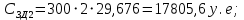    По формуле (4.8) определим 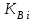 : :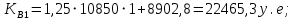   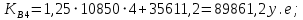  По формуле (4.1) определим  : :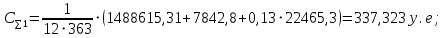 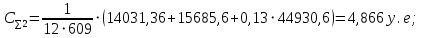  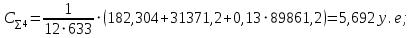  Список технологического оборудования и организационной оснастки с ценами приведен в таблице 4.2 Таблица 4.2 – Сводная ведомость технологического оборудования и организационной оснастки производственной зоны ТР
Все оборудование представленное в таблице 4.2 подобрано в соответствии с требованиями предъявляемыми к посту ТР, оборудование учитывает тип подвижного состава. Схема поста ТР представлена на рисунке 4.1.  Рисунок 4.1 – Схема поста ТР Заключение В ходе курсовой работы было выполнено моделирование работы зоны ТР дорожной ОАС на дороге 1 категории. В первом разделе была разработана концептуальная модель, а именно, была поставлена задача моделирования, проанализирована задача, выбрана исходная информация о системе, а также были определены параметры и переменные модели системы. Также было установлено содержание модели, обоснованы критерии моделирования. Во втором разделе приведен алгоритм соответствующей модели. В третьем разделе было произведено кодирование входных величин модели и составлена матрица спектра плана. Затем было произведено моделирование с помощью программы simsim.exe. Результаты моделирования представлены в этом же разделе. Также была рассчитана регрессионная модель и составлены уравнения регрессии для двух выбранных факторов, влияющих на поведение системы. Также были проверены на значимость коэффициенты уравнений регрессии. После этого была проведена проверка полученных моделей на адекватность. Проверка показала, что все модели являются адекватными. В четвертом разделе с помощью моделирования было установлено оптимальное количество постов ТР, при котором суммарные затраты минимальны. Это количество равно одному посту. При этом удельные затраты составили 4,45 у.е. Список литературы 1 Коваленко, Н. А. Техническая эксплуатация автомобилей : учеб. пособие / Н. А. Коваленко, В. П. Лобах, Н. В. Вепринцев. – Минск : Новое знание, 2008. – 352 с. 2 Коваленко, Н. А. Научные исследования и решение инженерных задач в сфере автомобильного транспорта : учеб. пособие. – Минск : Новое знание, 2011. – 298 с. 3 Коваленко, Н. А. Организация технического обслуживания и ремонта автомобилей : учеб. пособие / Н. А. Коваленко. – Минск : Новое знание; Москва : ИНФРА-М, 2016. – 229 с. 4 Напольский, Г. М. Техническое проектирование автотранспортных предприятий и станций технического обслуживания / Г.М. Напольский. Москва : Транспорт, 1993.271 с. 5 Проектирование предприятий автомобильного транспорта: учебник для студентов специальности «Техническая эксплуатация автомобилей» / М. М. Болбас, [и др.]; под ред. М. М. Болбаса. Минск : Адукацыя i выхаванне, 2004. – 528 с. 6 Советов, Б. Я. Моделирование систем: учебник для вузов по специальности АСУ / Б.Я. Советов, С.А. Яковлев. Москва : Высш. шк., 2001.271 с. 7 Тарасик, В. П. Математическое моделирование технических систем / В. П. Тарасик. – Минск : Дизайн ПРО, 2004. 640 с. 8 Техническая эксплуатация автомобилей /Под ред. Е.С. Кузнецова. Москва : Транспорт, 1992. 431 с. 9 ТКП 248-2010. Техническое обслуживание и ремонт автомобильных транспортных средств. Нормы и правила проведения. – Минск : Транстехника», 2010. 42 с. 10 ОНТП-01-91. Общесоюзные нормы технологического проектирования предприятий автомобильного транспорта. – Москва : Гипроавтотранс, 1991. – 184 с. Приложение А (Обязательное) Результаты экспериментов  Рисунок А.1 - Результаты первого эксперимента  Рисунок А.2 – Результаты второго эксперимента 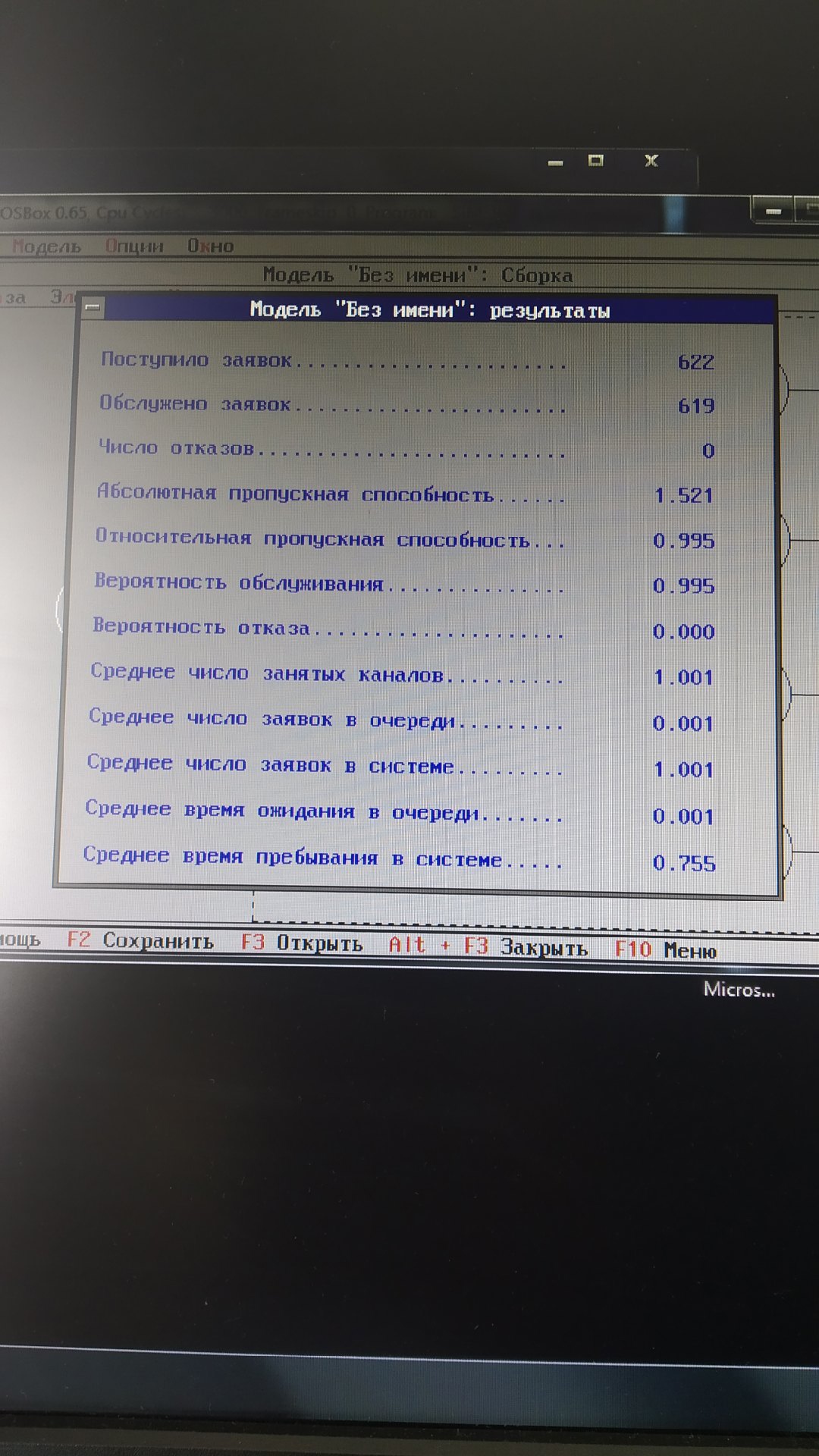 Рисунок А.3 – Результаты третьего эксперимента  Рисунок А.4 – Результаты четвертого эксперимента 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||