ЖБК 1 СРс. " Расчет трехпролетной двухэтажной рамы гражданского здания в соответствии с методикой и рекомендациями Еврокодов. Общие положения. Сбор нагрузок."

• Название: " Расчет трехпролетной двухэтажной рамы гражданского здания в соответствии с методикой и рекомендациями Еврокодов. Общие положения. Сбор нагрузок."
• Дата: 15.02.2023
• Размер: 115.06 Kb.
• Имя файла: ЖБК 1 СРс.docx
• Тип: Реферат; #938732

Министерство образования и науки Республики Казахстан

Международная образовательная корпорация

Казахская головная архитектурно-строительная академия



РЕФЕРАТ

Тема: " «Расчет трехпролетной двухэтажной рамы гражданского здания в соответствии с методикой и рекомендациями Еврокодов. Общие положения. Сбор нагрузок.»"

Выполнил: Базар А.Т

Группа: РПЗС 20-11

Проверила: Ажгалиева Б.А.

Алматы 2023 г.

Содержание

1. Расчет трехпролетной двухэтажной рамы гражданского здания в соответствии с методикой и рекомендациями Еврокодов. Общие положения. Сбор нагрузок.

2. Укрупненная сетка колонн второго этажа

3. Список литературы

Введение

Для здания второго этажа выполняется статический расчет трехпролетной двухэтажной плоской рамы. Для данных конкретных рам, из-за наличия температурного шва по оси, при расчете возможен учет только раздельного воздействия ветровой нагрузки на наветренные или подвстренные стороны рам здания. В рассмотренных расчетах учитывается возможность совместного воздействия встровой нагрузки на навстренные или подветренные стороны здания, что чаще встречается на практике.

- Расчеты выполнялись для трех случаев:

1. При использовании в методиках Еврокодов частных коэффициентов надежности, рекомендованных Еврокодами.

2. При использовании в методиках Евроколо частных дежности из национальных стандартов Рф (СНиП и СП).

3. По национальным стандартам РФ

Для всех трех случает выполнятся расчет арматуры в наиболее нагруженной.

Укрупненная сетка колонн второго этажа


Удорожание площади отводимой под строительство производственных зданий вызвало необходимость разработки двухэтажных производственных зданий с укрупненной сеткой колонн. Это конструктивное решение позволяет сэкономить до 30-40% площади территории, более эффективно использовать строительный объем здания, снизить стоимость используемых площадей, а также в ряде случаев целесообразно для организации технологического процесса. Двухэтажные многопролетные здания все чаще заменяют одноэтажные. Двухэтажные промышленные здания: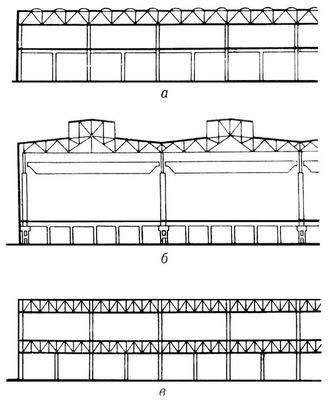



а — многопролетное здание со световыми фонарями и укрупнённой сеткой колонн в верхнем этаже; б — здание с нижним техническим этажом; в — здание с промежуточным техническим этажом.

Технологическое оборудование, создающее большие статические и динамические нагрузки, в таких зданиях располагают на первом этаже, а легкое оборудование – на втором. За счет этого конструкция междуэтажного перекрытия остается достаточно простой, уменьшается протяженность инженерных коммуникаций, т.к. имеется возможность обслуживания сразу двух этажей, а использование укрупненной сетки колонн позволяет располагать на втором этаже относительно легкое технологическое оборудование.

Возможность размещения на первом этаже различных коммуникаций позволяет отказаться от подвалов и подпольных каналов, что приводит к экономичному использованию объема здания. Наиболее эффективно такое размещение при значительном перепаде высот в пределах участка застройки, т.к. это приводит к уменьшению объемов земляных работ и позволяет устроить въезды на необходимых отметках на оба уровня.

Двухэтажные здания с укрупненной сеткой колонн верхнего этажа нашли широкое применение в отечественной и зарубежной практике для автомобильного производства и других отраслей машиностроения. Применение таких зданий обусловлено не только экономическими соображениями, но и технологическими особенностями производства. Яркими примерами являются – автомобильный завод «Фольксваген», завод двигателей и фургонов в Ганновере (Германия), автосборочные заводы «Крайслер» в Фентоне и Бельвидире (США) и др.

Чугунолитейный корпус Камского автомобильного завода (рисунок 1.7) одно из самых крупных двухэтажных производственных зданий в России. Его 18 размеры в плане - 715×241м, площадью застройки более 140 тыс. м2 [101], высота первого (технического) этажа - 8,4 м, сетка колонн - 12×6 м на первом этаже и 24×12 м - на втором.



Чугунолитейный корпус КамАЗа (Промстройпроект)

Стоимость единицы площади двухэтажного здания на 5-15% меньше, чем одноэтажного. Это обусловлено тем, что расходы на междуэтажное перекрытие, лестницы, лифты покрываются с избытком снижением стоимости земельного участка, покрытия, кровли, исключением стоимости подвалов, каналов и приямков. Также двухэтажные здания также более привлекательны с точки зрения эстетичности восприятия здания в застройке.

Имеется рама, состоящая из 3 горизонтальных и 4 вертикальных элементов. На горизонтальные элементы рамы действует вертикальная равномерно распределенная нагрузка q.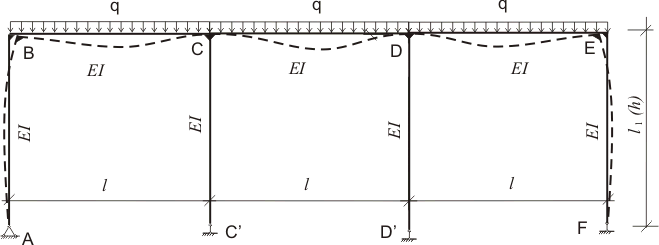



Рисунок 16.5. Расчетная схема для простой трехпролетной рамы.

1 этап

На этом этапе расчета такую раму можно рассматривать как неразрезную балку с 5 пролетами, равными по длине. Необходимо составить 4 уравнения трех моментов, но так как рама и нагрузка являются симметричными, т.е. M_B = M_E и М_С = М_D, то достаточно составить 2 уравнения:

2M_B1э(2l) + M_C1эl = - 6·R^ф₁; (12.1)

M_B1эl + 2M_C1э(2l) + М_D1эl = - 6·R^ф₂; (12.2)

где

R^ф₁ = А_B^ф = ql³/24 (12.3)

R^ф₂ = В_C^ф + А_D^ф = ql³/12 (12.4)

Тогда

2M_B1э(2l) + M_C1эl = - ql³/4; (12.5)

M_B1эl + 2M_C1э(2l) + М_D1эl = - ql³/2; (12.6)

4M_B1эl = - ql³/4 - M_C1эl; М_В1э = -ql²/16 - M_C1э/4 (13.1)

-ql³/16 - M_C1эl/4 + 4M_C1эl + М_C1эl = - ql³/2; 19M_C1эl/4 = -7ql³/16 (13.2)

Тогда

М_С1э = M_D1э = - 7ql²/76 ≈ - ql²/10.85; M_B1э = M_E1э = -ql²/16 + 7ql²/304 = - 12ql²/304 = -3ql²/76 ≈ - ql²/25.33 (13.3)

При этом угол наклона в точке C будет составлять:

θ^пр_C = -ql³/24EI - M_C1эl/3EI - M_D1эl/6EI = - ql³/24EI + 7ql³/(3·76EI) + 7ql³/(6·76EI) = ql³/228EI (13.5)

Такой угол наклона поперечного сечения является относительно небольшим и даже без дальнейших расчетов ясно, что сильно промежуточные стойки на окончательный результат не повлияют. Поэтому для упрощения расчетов значение момента на 2 этапе расчета можно принять равным М_2э = ql²/228.

Тем не менее продолжим.

Положительное значение угла поворота в начале рассматриваемого пролета показывает, что растягивающие напряжения будут возникать в правой части сечения стойки CC'. При определении угла наклона в точке D мы получили бы точно такой же результат, но с обратным знаком, что означает возникновение растягивающих напряжений в левой части сечения стойки DD'. Таким образом для дальнейших расчетов мы можем заменить промежуточные на положительные моменты, приложенные в точках С и D. M'_C = M'_D = 3ql³/228l = ql²/76.

2 этап

Как мы выяснили, определение момента на 2 этапе будет достаточно простым, если у рамы всего 3 стержня, при этом одинаковая длина, жесткость элементов и условия закрепления. Тогда значение момента М_С на втором этапе составило бы М_С2э = -ql²/(76·3) = -ql²/228 для всех элементов в точке С. Но в нашей раме 7 стержней и действие фиктивного момента будет распространяться на все 7 стержней, хотя и с разной долей эффективности. К тому же фиктивный момент приложен к двум стойкам. Т.е. для одних стержней (для левого горизонтального элемента и стойки в точке С) значение момента на втором этапе будет больше, а для других (правого горизонтального элемента в точке С) - меньше.

Если мы не будем обращать на это внимания и составим уравнения трех моментов, то можем определить значение момента на втором этапе для одного из трех стержней.

2M_B2э(2l) + M_C2эl = 0 (13.6)

M_B2эl + 2M_C2э(3l) + М_D2э(2l) = - 6·R^ф_С; (13.7)

где фиктивная опорная реакция в точке В слева равна нулю, так как мы прикладываем моменты (для упрощения расчетов) чуть правее точки С и чуть левее точки D (другими словами мы рассекаем раму так, что обе стойки попадают в среднее сечение). Это также означает, что сами по себе эти моменты первого уравнения поворота на опоре С не создают, а являются лишь следствием момента, заменяющего стойку. Другими словами, каково бы ни было значение момента в точке С, значение момента в точке В в данном случае будет в 4 раза меньше и будет иметь обратный знак. Соответственно фиктивная опорная реакция для второго уравнения согласно расчетной схеме 3.3, таблицы 315.1 составит:

R^ф_С = В_C^ф + А_D^ф = 3M'l/6 = ql³/(76·2) = ql³/152  (13.8)

Тогда

4M_B2эl = - M_C2эl;  M_B2э = - M_C2э/4 (491.16.4)

- M_C2эl/4 + 6M_C2эl + 2М_C2эl = - 6ql³/152; 31M_C2эl/4 = -6ql³/152 (13.9) 

М_С2э = M_D2э = - 3ql²/589; M_B2э = M_E2э = 3ql²/(589·4) = 3ql²/2356 (14.1)

Судя по знаку - это М_С^лев_2э. Тогда уточненное значение момента слева от стойки СС' составит:

М^лев_C = -7ql²/76 - 3ql²/589 = -4351ql²/44764 ≈ -ql²/10.29 (14.2)

Т.е. в итоге максимальное изменение значения момента составит 10.85/10.29 = 1.055 раза или 5.5% (где 10.85 и 10.29 - знаменатели значений моментов первого и второго этапа).

В целом, для того, чтобы узнать значение М_С^прав_2э, нужно рассматривать влияние каждой стойки отдельно, т.е. составить и решить 2 системы из 4 уравнений, так как в данном случае нагрузка будет несимметричной, причем уравнения нужно составлять очень внимательно. Затем на основании решения 2 систем уравнений построить эпюры моментов отдельно для каждого фиктивного момента, затем суммарную эпюру и уже по этой суммарной эпюре можно определить значения моментов 2 этапа. В итоге мы узнаем, что М_С^прав_2э будет немного меньше (примерно на 1/6), чем -М_С^лев_2э.

Вот только, на мой взгляд, в данном случае в этом нет совершенно никакой необходимости. Тем более, когда речь идет о расчете рамы, которая будет выполнена в единственном экземпляре.

Достаточно и того, что мы определили максимально возможное изменение момента для левого горизонтального элемента. Для упрощения расчетов и повышения надежности рамы изменение момента М_С^прав_2э вообще можно не учитывать, тогда

3 этап

Уточненные значения моментов для рассматриваемых элементов рамы составят:

М^с_С = - 2·3ql²/589 ≈ -ql²/98.2  (14.3)

М^лев_С ≈ -ql²/10.29  (14.4)

М^пр_С = М_С1э ≈ ql²/10.85  (14.5)

Более того, и для стойки можно принять большее значение расчетного момента, например, равным фиктивному моменту с обратным знаком -М'_С = -ql²/76. Еще более того, для правого горизонтального элемента мы для большей надежности можем не просто оставить так как есть значение первого этапа расчетов, а и увеличить его на значение момента второго этапа, в итоге М^лев_С = М^пр_С.

У механиков есть такое неписанное правило: чем проще система (т.е. чем меньше в ней деталей и узлов сопряжения), тем она надежнее. Это же можно сказать и о расчетах: чем проще расчет, тем он надежнее.

Например, при расчетах на втором этапе мы где-то ошиблись со знаками (при таком обилии данных это бывает), в результате значения моментов справа и слева от промежуточных стоек поменяются местами. Между тем, если задаться соответствующим коэффициентом надежности по нагрузке, учитывающим возможные изменения момента при наличии вертикальных стоек и просто умножить значения момента первого этапа на этот коэффициент, то возможное влияние указанной ошибки, как и других возможных ошибок будет нивелировано, а кроме того сам расчет значительно упростится.

Более того, чем больше пролетов в раме, тем меньше будет в итоге влияние промежуточных стоек. Ведь при этом углы наклона поперечных сечений на промежуточных опорах будут стремиться к нулю, а значения моментов на промежуточных опорах будут стремиться к -ql²/12, а значит и балки в таких пролетах все больше будут подходить под определение балки с жестко защемленными опорами, у которых угол поворота поперечного сечения на опорах равен нулю. Так что для таких рам даже без первого этапа расчетов можно обойтись, если использовать соответствующий коэффициент надежности и учитывать то, что моменты для горизонтальных элементов в крайних пролетах будут отличаться от моментов в промежуточных пролетах. В итоге чем более сложной изначально является рама, тем более простым может оказаться расчет, как ни парадоксально это звучит.

Общий вывод: Для упрощения расчетов многопролетных простых рам влиянием промежуточных стоек на изменение угла поворота горизонтальных элементов можно пренебречь, задавшись соответствующим дополнительным коэффициентом надежности по нагрузке, учитывающим возможное изменение момента γ_нм.

А вот какое именно лучше принять значение коэффициента надежности по нагрузке, зависит от множества факторов, частично мы их рассмотрели в 1 примере расчета.

Возможные значения коэффициентов надежности по нагрузке при упрощенном расчете рам

1. Рамы, элементы которых имеют одинаковую длину, жесткость и условия закрепления на опорах.

1.1. Для однопролетной рамы определять дополнительный коэффициент надежности по нагрузке нет необходимости, так как можно сразу воспользоваться результатами расчета такой рамы.

1.2. Для двухпролетной рамы при действии равномерно распределенной нагрузки в обеих пролетах определять дополнительный коэффициент надежности по нагрузке также нет необходимости, так как угол поворота на промежуточной опоре будет равен нулю.

1.3. Для трехпролетной рамы, как мы выяснили выше,  дополнительный коэффициент нагрузки можно определить следующим образом. Так как максимальное изменение момента составляет 5.5%, то γ_нм1.3 = 1 + 0.055 = 1.055.

1.4. Для рам с 4 пролетами значение дополнительного коэффициента надежности по нагрузке согласно формуле (13.2) может составлять γ_нм1.4 = 1.04.

1.5. Для рам с 5 и более пролетами значение дополнительного коэффициента надежности по нагрузке будет еще меньше. При расчете таких рам можно пользоваться γ_нм1.5 = 1.04.

2. Рамы, элементы которых имеют разную длину и жесткость, или разные условия закрепления на опорах.

2.1 Если у стоек снизу не шарнирная опора, а жесткое защемление, то это, как мы уже выяснили, приведет к увеличению расчетного момента второго этапа в 1.2 раза. Таким образом значение коэффициента составит γ_нм2.1 = 1 + 0.055·1.2 = 1.067. 

2.2. Если длина стоек в 2 раза меньше длин горизонтальных элементов или жесткость стоек в 2 раза больше, чем горизонтальных элементов, то это также приведет к увеличению расчетного момента, принимаемого на 2 этапе, Максимальное изменение, как мы выяснили будет составлять 1.5 раза. Соответственно в этом случае для упрощения расчетов можно принимать коэффициент γ_нм2.2 = 1 + 0.055·1.5 = 1.083.

2.3. Если длина стоек в 2 раза больше длин горизонтальных элементов или жесткость стоек в 2 раза меньше, чем горизонтальных элементов, то это приведет к уменьшению расчетного момента, принимаемого на 2 этапе, Максимальное изменение, как мы выяснили будет составлять 0.6 раза. Соответственно в этом случае для упрощения расчетов можно принимать коэффициент γ_нм2.2 = 1 + 0.055·0.6 = 1.033.

2.4. Если все стойки имеют длину, близкую к нулевой, или жесткость, близкую к бесконечной. То все горизонтальные элементы рамы рассчитываются как жестко защемленные рамы на обеих опорах. Никаких дополнительных коэффициентов при этом не требуется.

2.5. Если стойки имеют длину, близкую к бесконечной или жесткость близкую к нулевой, то никакого влияния такие стойки на горизонтальные элементы рамы не оказывают и их можно рассчитывать как простую неразрезную балку. Никаких дополнительных коэффициентов при этом не требуется.

Примечание: При промежуточном значении длин и(или) жесткостей значение дополнительного коэффициента можно определить интерполяцией.

3. Если у многопролетной рамы одноэтажного здания горизонтальные элементы будут сверху и снизу, образуя замкнутые контуры, и при этом опирание внизу остается шарнирное, то при одинаковой вертикальной нагрузке на верхние и на нижние горизонтальные элементы, при одинаковой жесткости и длине элементов расчетная длина промежуточных стоек в результате деформации уменьшится в 2 раза. Т.е. в этом случае можно принимать коэффициент γ_нм3 = γ_нм2.2 = 1.0.83.

4. 1. Для рам многоэтажных зданий, горизонтальные элементы которых загружены одинаковой равномерно распределенной нагрузкой, кроме того соблюдаются условия п.3, коэффициент γ_нм4.1 = γ_нм2.2 = 1.083

4.2. Если у рамы многоэтажного здания нижние стойки имеют жесткое защемление и соответственно горизонтальные элементы на уровне низа стоек отсутствуют, то в этом случае значение коэффициента можно принимать в пределах γ_нм4.2 = 1.067÷1.083.

В целом, как я уже говорил в начале, практически для любой плоской рамы при расчете на вертикальную равномерно распределенную нагрузку можно принимать дополнительный коэффициент надежности по нагрузке 1.1, а если колонны рамы будут иметь меньшую длину и жесткость чем горизонтальные элементы, а так оно чаще всего и бывает, то достаточно и коэффициента 1.05.

Список литературы

1. Долгун А.И. Строительные конструкции: учебник для студентов. – М.: изд. центр «Академия», 2013. – 432 с.

2. Добромыслов А.Н. Железобетонные конструкции.- М.: Изд-во АСВ, 2012.- 464 с.

3. Евстифеев В.Г. Железобетонные и каменные конструкции. В 2 ч. Ч.1. Железобетонные конструкции: учебник для студентов. – М.: изд. центр «Академия», 2011. – 432 с.

4. Евстифеев В.Г. Железобетонные и каменные конструкции. В 2 ч. Ч.2. Каменные и армокаменные конструкции: учебник для студентов. – М.: изд. центр «Академия», 2011. – 192 с.

5. Яковлев С.К. Расчет железобетонных конструкций по Еврокоду EN1992: в 2 ч.: учебно-методическое пособие / С.К. Яковлев, Я.И. Мысляева; Москва: МГСУ, 2015. Ч.1: Изгибаемые и сжатые железобетонных элементы без предварительного напряжения. Определение снеговых, ветровых и крановых нагрузок. Сочетание воздействий. Москва: МГСУ, 2015. 204 с.