ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ Лобачев Р.Н.. Седловая точка отсутствует. Ищем решение игры в смешанных стратегиях
 Скачать 121.44 Kb. Скачать 121.44 Kb.
|
|
№1. Исходные данные:
Нижняя цена игры a = max(ai) = 8, которая указывает на максимальную чистую стратегию A2. Верхняя цена игры b = min(bj) = 9. Седловая точка отсутствует. Ищем решение игры в смешанных стратегиях. Графически: Для 1го игрока v = 14 + (8 - 14)p2 v = 6 + (9 - 6)p2 Откуда p1 = 1/9 p2 = 8/9 Цена игры, v = 26/3 Для 2го игрока: 14q1+6q2 = 26/3 8q1+9q2 = 26/3 q1+q2 = 1 Решая эту систему, находим: q1 = 1/3. q2 = 2/3. 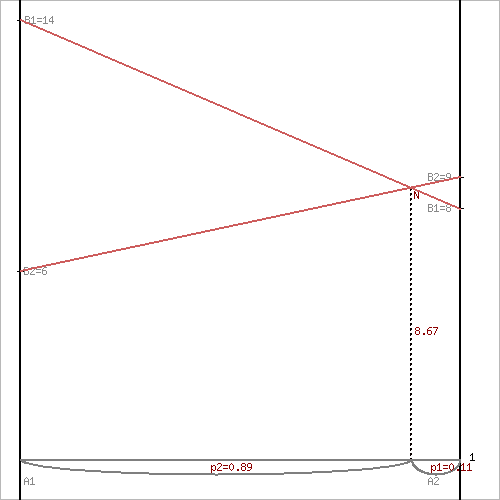 Аналитическое решение: Ответ: v= 26/3 P(1/9, 8/9), Q(1/3, 2/3). №2. Исходные данные:
Нижняя цена игры a = max(ai) = -1, которая указывает на максимальную чистую стратегию A1. Верхняя цена игры b = min(bj) = 3. Седловая точка отсутствует. Ищем решение в смешанных стратегиях. В платежной матрице отсутствуют доминирующие строки/столбцы. Составляем пары двойственных задач: найти минимум функции F(x) при ограничениях (для игрока II): 9x1+4x2+7x3 ≥ 1 2x1+x2+8x3 ≥ 1 5x1+6x2 ≥ 1 F(x) = x1+x2+x3 → min найти максимум функции Z(y) при ограничениях (для игрока I): 9y1+2y2+5y3 ≤ 1 4y1+y2+6y3 ≤ 1 7y1+8y2 ≤ 1 Z(y) = y1+y2+y3 → max Решаем задачу на максимум. Приводим к каноническому виду: 9y1+2y2+5y3+y4 = 1 4y1+y2+6y3+y5 = 1 7y1+8y2+y6 = 1 Опорный план:
В качестве ведущего выберем столбец, соответствующий переменной y3, так как это наибольший коэффициент по модулю. 2я строка является ведущей:
Вместо переменной y5 в план 1 войдет переменная y3.
|
