ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ Лобачев Р.Н.. Седловая точка отсутствует. Ищем решение игры в смешанных стратегиях

• Название: Седловая точка отсутствует. Ищем решение игры в смешанных стратегиях
• Дата: 05.04.2023
• Размер: 121.44 Kb.
• Имя файла: ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ Лобачев Р.Н..docx
• Тип: Документы; #1040493
• страница: 3 из 4

Ответ:

P(0,0,0,1)
Q(0,0,0,1)
№5.

Исходные данные:

Игроки	B1	B2	a = min(Ai)
A1	2	4	2
A2	8	3	3
b = max(Bi)	8	4

Нижняя цена игры a = max(a_i) = 3, которая указывает на максимальную чистую стратегию A₂.
Верхняя цена игры b = min(b_j) = 4. Седловая точка отсутствует. Ищем решение в смешанных стратегиях аналитически:






Ответ: y=3⁵/₇
P(⁵/₇, ²/₇)
Q(¹/₇, ⁶/₇)

№6.

Исходные данные:

Игроки	B1	B2	B3	B4	a = min(Ai)
A1	5	6	0	7	0
A2	1	1	6	5	1
A3	4	8	9	8	4
A4	1	4	6	8	1
b = max(Bi)	5	8	9	8

Нижняя цена игры a = max(a_i) = 4, которая указывает на максимальную чистую стратегию A₃.
Верхняя цена игры b = min(b_j) = 5. Седовая точка отсутствует. Ищем решение в смешанных стратегиях.

Стратегия A₃ доминирует над стратегией A₂ (все элементы строки 3 больше или равны значениям 2-ой строки), следовательно, исключаем 2-ую строку матрицы. Вероятность p₂ = 0.
Стратегия A₃ доминирует над стратегией A₄ (все элементы строки 3 больше или равны значениям 4-ой строки), следовательно, исключаем 4-ую строку матрицы. Вероятность p₄ = 0:

Игроки	B1	B2	B3	B4
A1	5	6	0	7
A3	4	8	9	8

С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₂ (все элементы столбца 1 меньше элементов столбца 2), следовательно, исключаем 2-й столбец матрицы. Вероятность q₂ = 0.
С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₄ (все элементы столбца 1 меньше элементов столбца 4), следовательно, исключаем 4-й столбец матрицы. Вероятность q₄ = 0:

Игроки	B1	B3
A1	5	0
A3	4	9

Решаем аналитически:






Ответ: y=4¹/₂
P(¹/₂, 0, ¹/₂, 0)
Q(⁹/₁₀, 0, ¹/₁₀, 0)
№7а.

Исходные данные:

Игроки	B1	B2	B3	B4	a = min(Ai)
A1	5	0	9	7	0
A2	4	8	8	2	2
A3	1	5	6	1	1
A4	4	0	7	0	0
b = max(Bi)	5	8	9	7

Нижняя цена игры a = max(a_i) = 2, которая указывает на максимальную чистую стратегию A₃.
Верхняя цена игры b = min(b_j) = 5. Седовая точка отсутствует. Ищем решение в смешанных стратегиях.

Стратегия A₁ доминирует над стратегией A₄ (все элементы строки 1 больше или равны значениям 4-ой строки), следовательно, исключаем 4-ую строку матрицы. Вероятность p₄ = 0.
Стратегия A₂ доминирует над стратегией A₃ (все элементы строки 2 больше или равны значениям 3-ой строки), следовательно, исключаем 3-ую строку матрицы. Вероятность p₃ = 0:

Игроки	B1	B2	B3	B4
A1	5	0	9	7
A2	4	8	8	2

С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₃ (все элементы столбца 1 меньше элементов столбца 3), следовательно, исключаем 3-й столбец матрицы. Вероятность q₃ = 0:

Игроки	B1	B2	B4
A1	5	0	7
A2	4	8	2

Решаем игру графически. Для 1го игрока:

v = 0 + (8 - 0)p₂
v = 7 + (2 - 7)p₂
Откуда
p₁ = ⁶/₁₃
p₂ = ⁷/₁₃
Цена игры, v = ⁵⁶/₁₃

Для 2го игрока:

7q₃ = ⁵⁶/₁₃
8q₂+2q₃ = ⁵⁶/₁₃
q₂+q₃ = 1
Решая эту систему, находим:
q₂ = ⁵/₁₃.
q₃ = ⁸/₁₃.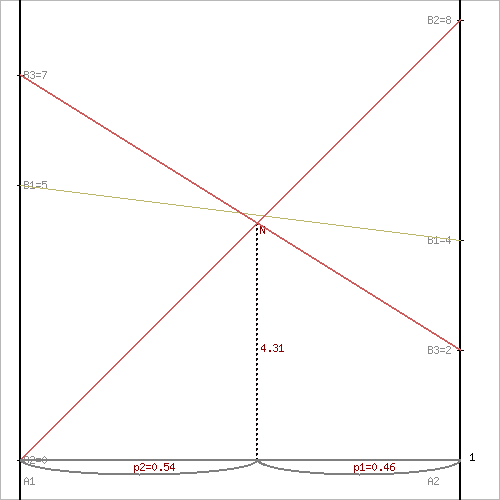



Ответ:
v = ⁵⁶/₁₃.

P(⁶/₁₃, ⁷/₁₃), Q(0, ⁵/₁₃, ⁸/₁₃).
№7б.

Исходные данные:

Игроки	B1	B2	B3	B4	a = min(Ai)
A1	7	5	1	7	1
A2	4	8	5	9	4
A3	9	5	0	1	0
A4	4	6	2	2	2
b = max(Bi)	9	8	5	9