Лекция№20. Выпуклые множества и выпуклые функционалы. Теорема Хана Банаха
 Скачать 48.05 Kb. Скачать 48.05 Kb.
|
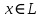 он разделяет множества он разделяет множества 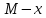 и и 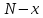 . .Из теоремы Хана — Банаха легко получается следующая теорема об отделимости выпуклых множеств в линейном пространстве, имеющая многочисленные применения. Теорема 5. Пусть 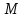 и и 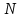 — выпуклые множества в действительном линейном пространстве — выпуклые множества в действительном линейном пространстве 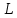 , причем ядро хотя бы одного из них, скажем , причем ядро хотя бы одного из них, скажем 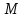 , не пусто и не пересекается с другим множеством. Тогда существует ненулевой линейный функционал. на , не пусто и не пересекается с другим множеством. Тогда существует ненулевой линейный функционал. на 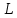 , разделяющий , разделяющий 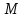 и и 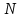 . .Доказательство. Без ограничения общности можно считать, что точка 0 принадлежит ядру 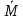 множества множества 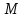 . (Иначе мы рассмотрели бы множества . (Иначе мы рассмотрели бы множества 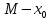 и и 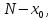 где где 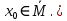 Пусть Пусть 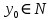 , тогда точка , тогда точка 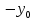 принадлежит ядру множества принадлежит ядру множества 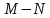 а 0 принадлежит ядру а 0 принадлежит ядру 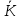 множества множества 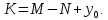 Так как Так как 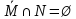 , то 0 не принадлежит ядру , то 0 не принадлежит ядру 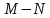 и и 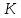 . Пусть . Пусть 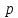 — функционал Минковского для — функционал Минковского для 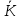 . Тогда . Тогда 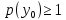 поскольку поскольку 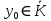 . Введем линейный функционал . Введем линейный функционал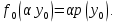 Он определен на одномерном пространстве, состоящем из элементов вида 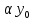 , и удовлетворяет условию , и удовлетворяет условию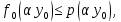 поскольку 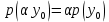 при при 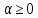 , и , и 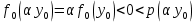 при при 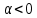 . По теореме Хана — Банаха функционал . По теореме Хана — Банаха функционал 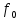 . можно продолжить до линейного функционала . можно продолжить до линейного функционала 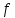 , определенного на всем , определенного на всем 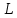 и удовлетворяющего на и удовлетворяющего на 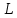 условию условию 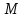 и и 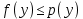 . Отсюда следует, что . Отсюда следует, что 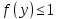 при при 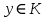 и в то же время и в то же время 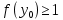 . Таким образом, . Таким образом, 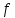 разделяет множества разделяет множества 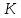 и и 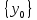 , а следовательно, , а следовательно, 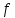 разделяет разделяет 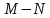 и {0}; но тогда и {0}; но тогда 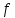 разделяет множества разделяет множества 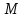 и и 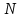 . .Теорема доказана. |
