Лекция№20. Выпуклые множества и выпуклые функционалы. Теорема Хана Банаха
 Скачать 48.05 Kb. Скачать 48.05 Kb.
|
Функционал Мннковского. Пусть 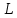 — произвольное линейное пространство и — произвольное линейное пространство и 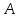 — выпуклое тело в — выпуклое тело в 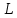 , ядро которого содержит точку 0. Функционал , ядро которого содержит точку 0. Функционал 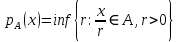 (6) (6)называется функционалом Минковского выпуклого тела 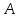 . .Теорема 3. Функционал Минковского (6) — однородно- выпуклый и неотрицательный. Обратно, если 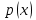 — произвольный однородно-выпуклый неотрицательный функционал на линейном пространстве — произвольный однородно-выпуклый неотрицательный функционал на линейном пространстве 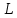 и и 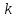 — положительное число, то — положительное число, то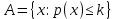 (7) (7)есть выпуклое тело, ядром которого служит множество 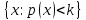 (содержащее точку 0). Если в (7) (содержащее точку 0). Если в (7) 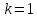 , то исходный функционал , то исходный функционал 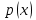 есть функционал Минковского для есть функционал Минковского для 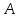 . .Доказательство. Для всякого 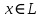 элемент элемент 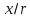 принадлежит принадлежит 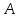 , если , если 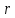 достаточно велико; поэтому величина определяемая равенством (6), неотрицательна и конечна. Проверим положительную однородность функционала (6). Если достаточно велико; поэтому величина определяемая равенством (6), неотрицательна и конечна. Проверим положительную однородность функционала (6). Если 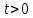 и и 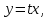 то то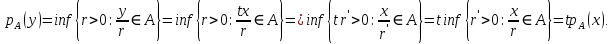 (8) (8)Проверим выпуклость 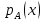 . Пусть . Пусть 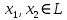 и и 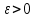 произвольно. Выберем числа произвольно. Выберем числа 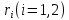 так, что так, что 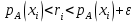 ; тогда ; тогда 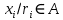 . Положим . Положим 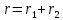 , тогда точка , тогда точка 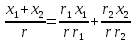 принадлежит отрезку с концами принадлежит отрезку с концами 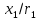 и и 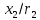 . В силу выпуклости . В силу выпуклости 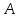 этот отрезок, а значит, и точка этот отрезок, а значит, и точка 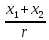 принадлежат принадлежат 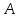 , откудa , откудa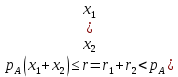 . .Так как 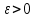 здесь произвольно, то здесь произвольно, то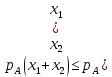 Следовательно, 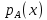 удовлетворяет условиям (2') и (3), а потому это — неотрицательный однородно-выпуклый функционал. удовлетворяет условиям (2') и (3), а потому это — неотрицательный однородно-выпуклый функционал.Рассмотрим теперь множество (7). Если 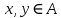 и и 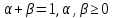 , то , то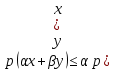 т. е. 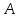 выпукло. Далее, пусть выпукло. Далее, пусть 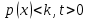 и и 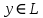 , тогда , тогда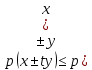 . .Если 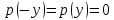 , то , то 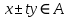 при всех при всех 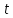 если же хотя бы одно из неотрицательных чисел если же хотя бы одно из неотрицательных чисел 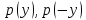 отлично от 0, то отлично от 0, то 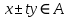 при при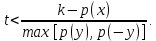 Непосредственно из введенных определений ясно, что р служит функционалом Минковского для множества 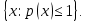 Итак, введя понятие функционала Минковского, мы установили соответствие между неотрицательными однородно-выпук- лыми функционалами и выпуклыми телами с ядром, содержащим точку 0. Примеры. 1. При 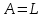 имеем, очевидно, имеем, очевидно,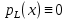 . .Пусть 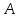 — шар с центром 0 и радиусом — шар с центром 0 и радиусом 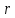 в в 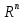 . Тогда . Тогда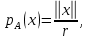 где 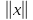 — длина вектора — длина вектора 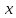 . .Пусть 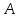 — «слой» — «слой» 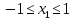 в пространстве в пространстве 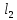 последовательностей последовательностей 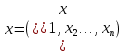 . Тогда . Тогда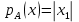 . .Замечания. 1. Иногда удобно рассматривать однородно- выпуклые функционалы, которые могут принимать не только конечные значения, но и значение 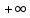 (но не (но не 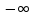 ). Тогда из равенства ). Тогда из равенства 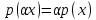 (где (где 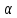 > 0) следует, что > 0) следует, что 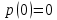 или или 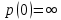 . Легко проверить, что в этом последнем случае можно, не нарушая однородной выпуклости функционала, изменить его значение в одной точке, положив . Легко проверить, что в этом последнем случае можно, не нарушая однородной выпуклости функционала, изменить его значение в одной точке, положив 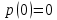 вместо вместо 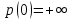 . Так обычно и делают. . Так обычно и делают.Если 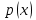 — однородно-выпуклый, но не обязательно конечный, функционал, то — однородно-выпуклый, но не обязательно конечный, функционал, то 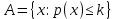 есть выпуклое множество, но не обязательно выпуклое тело. Обратно, если есть выпуклое множество, но не обязательно выпуклое тело. Обратно, если 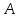 — произвольное выпуклое множество, содержащее точку 0, то для него можно определить функционал Минковского формулой (6), но при этом придется для — произвольное выпуклое множество, содержащее точку 0, то для него можно определить функционал Минковского формулой (6), но при этом придется для 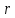 допускать и значение допускать и значение2. Если 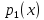 и и 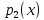 — однородно-выпуклые функционалы, то таковы же — однородно-выпуклые функционалы, то таковы же 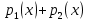 и и 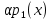 при при 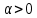 . Далее, если . Далее, если 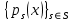 — произвольное семейство однородно-выпуклых функционалов, то таков и функционал — произвольное семейство однородно-выпуклых функционалов, то таков и функционал 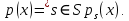 В частности, верхняя грань В частности, верхняя грань 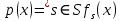 любого непустого множества линейных функционалов на L есть однородно-выпуклый функционал. Воспользовавшись теоремой Хана — Банаха, легко показать^ что так можно представить всякий (конечный) однородно-выпуклый функционал. любого непустого множества линейных функционалов на L есть однородно-выпуклый функционал. Воспользовавшись теоремой Хана — Банаха, легко показать^ что так можно представить всякий (конечный) однородно-выпуклый функционал.Упражнение. Множество 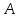 в линейном пространстве в линейном пространстве 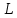 называется поглощающим, если для всякого называется поглощающим, если для всякого 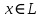 существует такое существует такое 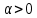 , что , что 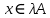 для всех для всех 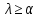 . Доказать, что выпуклое множество . Доказать, что выпуклое множество 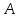 —поглощающее в том и только том случае, если его ядро содержит точку —поглощающее в том и только том случае, если его ядро содержит точку 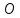 . .4. Теорема Хана — Банаха. Пусть 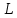 — действительное линейное пространство и — действительное линейное пространство и 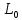 — некоторое его подпространство. Пусть, далее, на подпространстве — некоторое его подпространство. Пусть, далее, на подпространстве 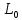 задан некоторый линейный: функционал задан некоторый линейный: функционал 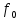 . Линейный функционал . Линейный функционал 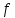 , определенный на всем пространстве , определенный на всем пространстве 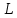 , называется продолжением функционала , называется продолжением функционала 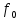 , если , если 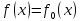 для всех для всех 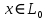 Задача о продолжении линейного функционала часто встречается в анализе. Основную роль во всем этом круге вопросов^ играет следующая теорема. Теорема 4 (Хан —Банах). Пусть 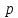 — однородно-выпуклый функционал, определенный на действительном линейном: пространстве — однородно-выпуклый функционал, определенный на действительном линейном: пространстве 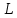 , и пусть , и пусть 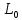 — линейное подпространство в — линейное подпространство в 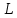 . Если . Если 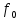 — линейный функционал на — линейный функционал на 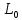 , подчиненный на , подчиненный на 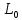 функционалу функционалу 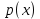 , т. е. если на , т. е. если на 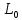 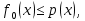 (9) (9)то 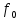 может быть продолжен до линейного функционала может быть продолжен до линейного функционала 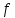 на на 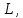 подчиненного подчиненного 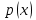 на всем на всем 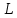 . .Доказательство. Покажем, что если 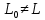 , то функционал , то функционал 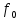 можно продолжить с можно продолжить с 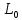 на некоторое большее подпространство на некоторое большее подпространство 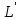 с сохранением условия (9). Действительно», пусть с сохранением условия (9). Действительно», пусть 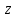 — произвольный элемент из L, не принадлежащий и пусть — произвольный элемент из L, не принадлежащий и пусть 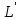 — подпространство, порожденное — подпространство, порожденное 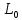 и и 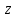 . Каждый элемент из . Каждый элемент из 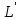 имеет вид имеет вид 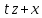 , где , где |
