рр. 060 Механические колебания и волны
 Скачать 2.05 Mb. Скачать 2.05 Mb.
|
|
, м и 2) 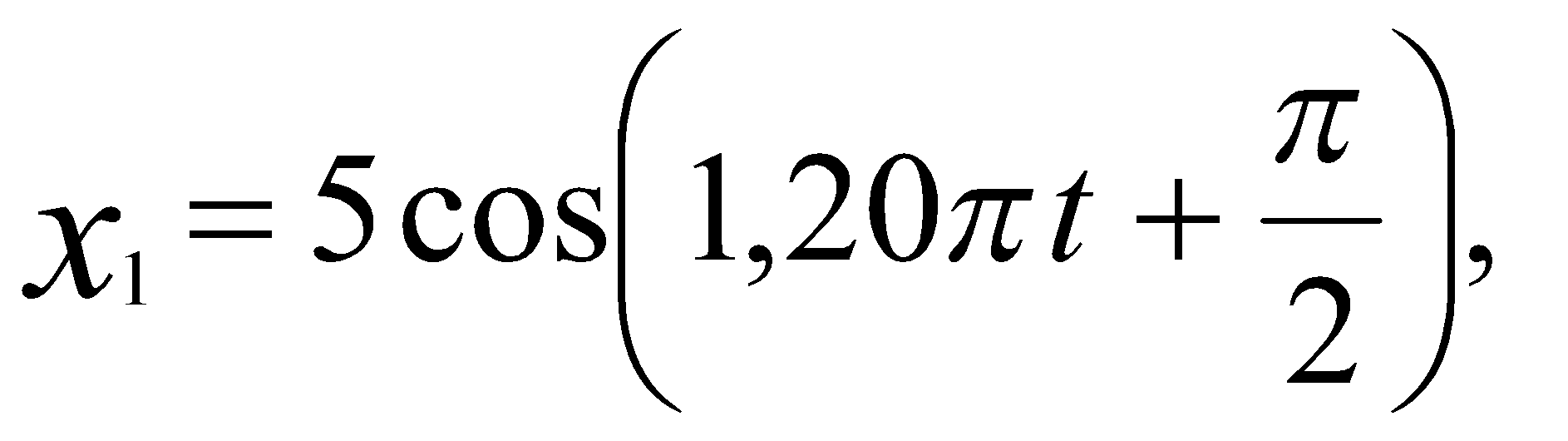 м и м и 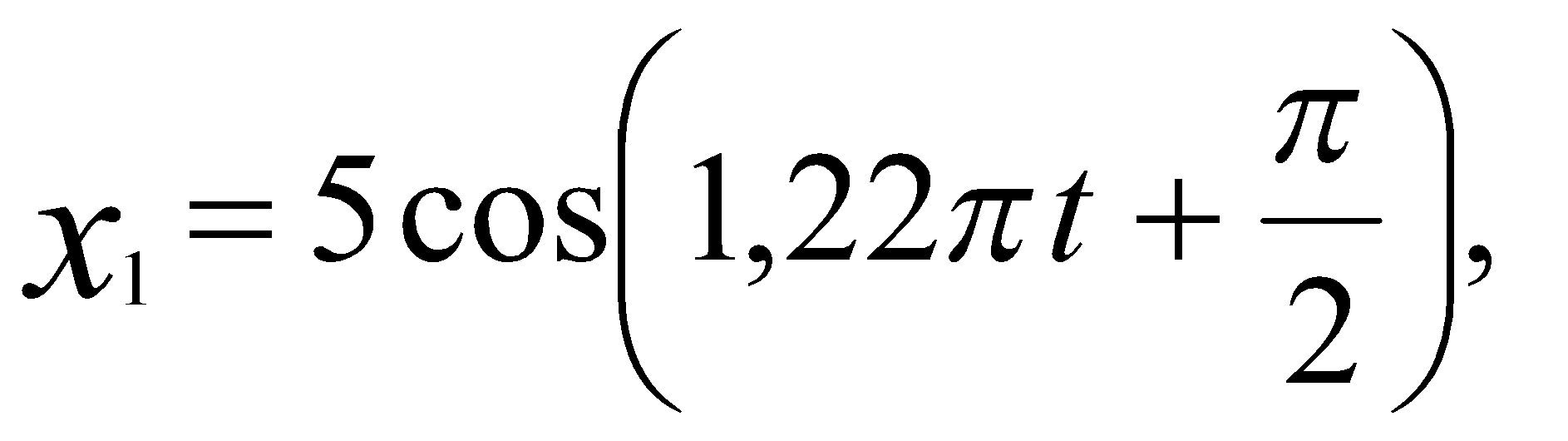 м. м.3) 4) 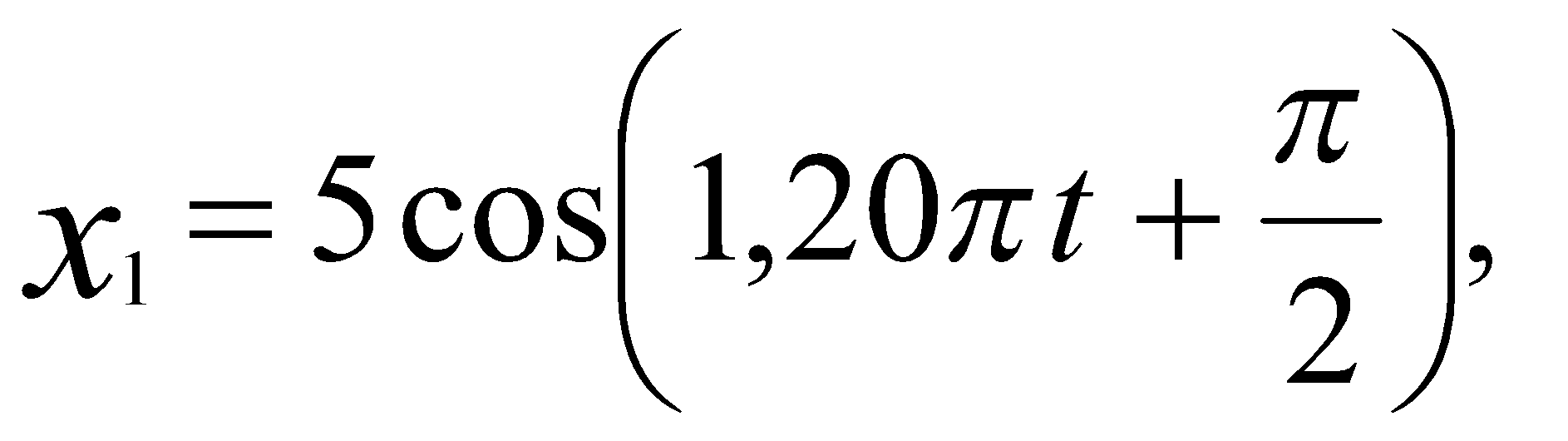 м и м и 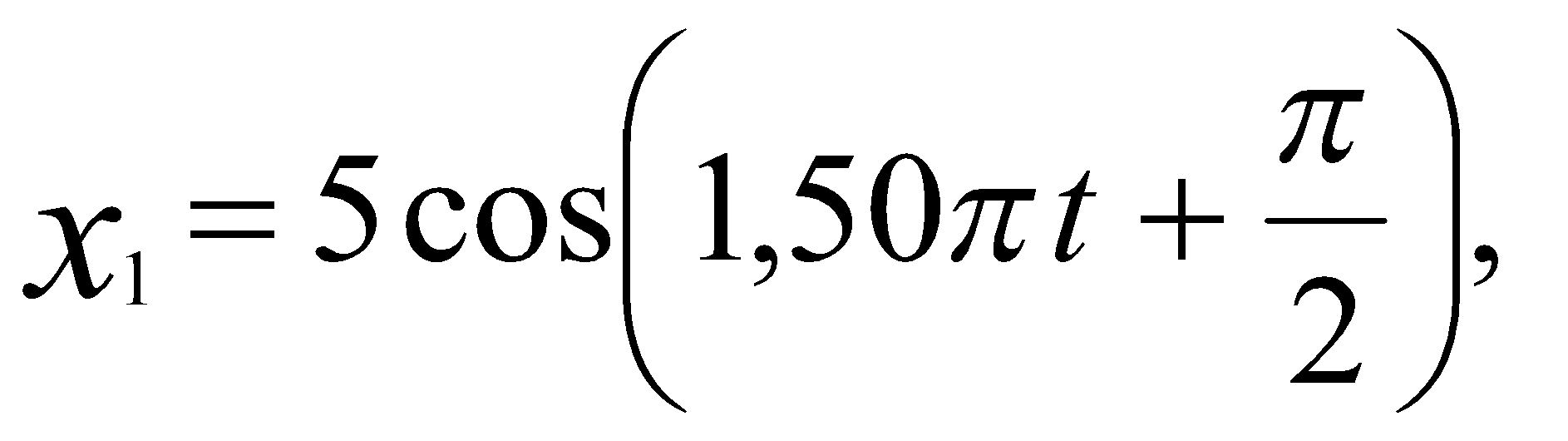 м. м.Результирующее движение называется биением в (во) … случае. 1) 1 2) 2 3) 3 4) 4 :2 4. [Уд1] (ВО1) Складываются два гармонических колебания, происходящих в одном направлении: 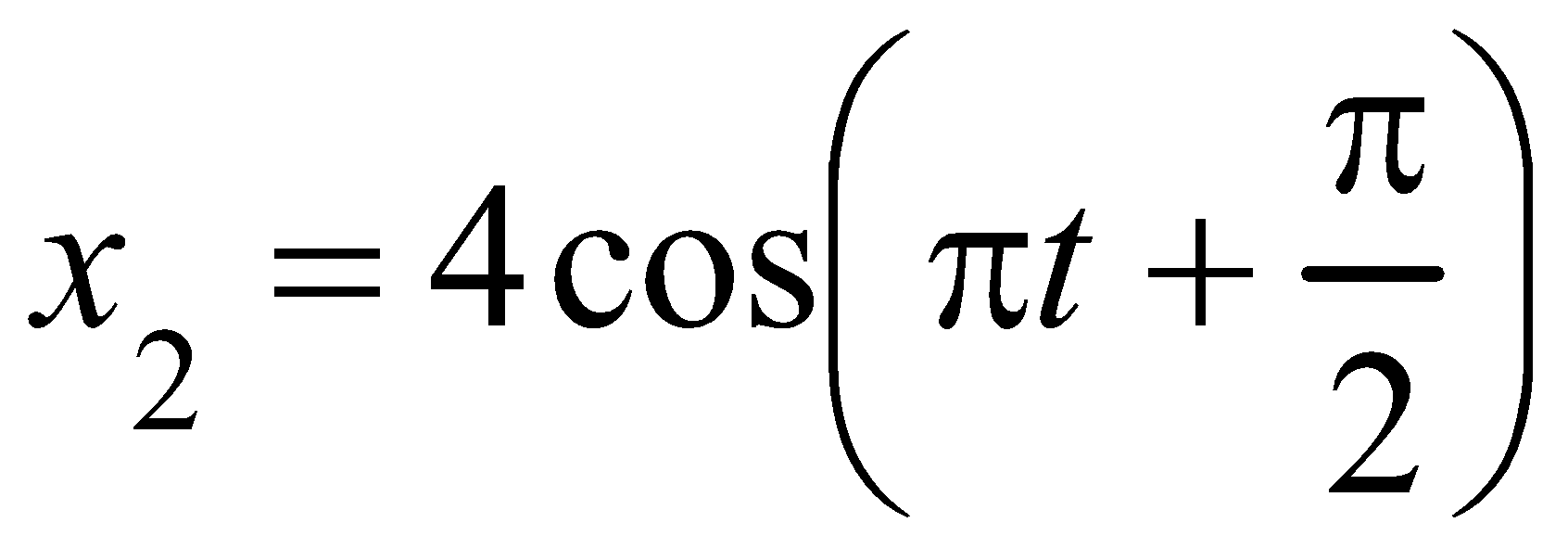 см и см и 1) 7 2) 5 3) 3,5 4) 1 :2 5. [Уд1] (ВО1) Результат сложения двух гармонических колебаний одного направления с одинаковыми амплитудами и близкими частотами описывает уравнение 1) х = Acos (ω0t +ϕo) 2) A2 = A12 +A22 + 2A1A2 cos Δϕ 3) x = 2A cos 4) 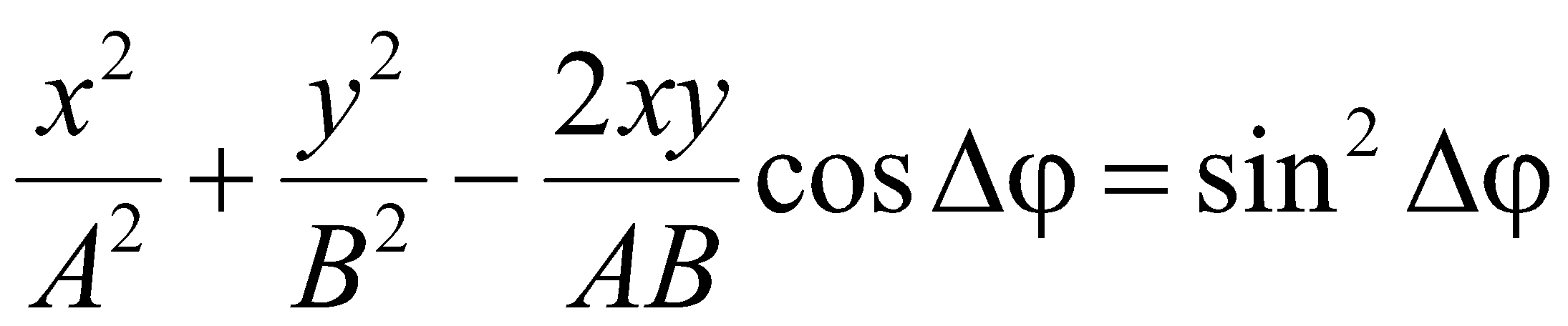 :3 6. [Уд1] (ВО1) Уравнение траектории при сложении двух гармонических колебаний взаимно перпендикулярных направлений с отличающимися амплитудами и одинаковыми частотами – 1) х = Acos (ω0t +ϕo) 2) A2 = A12 +A22 + 2A1A2 cos Δϕ 3) x = 2A cos 4) 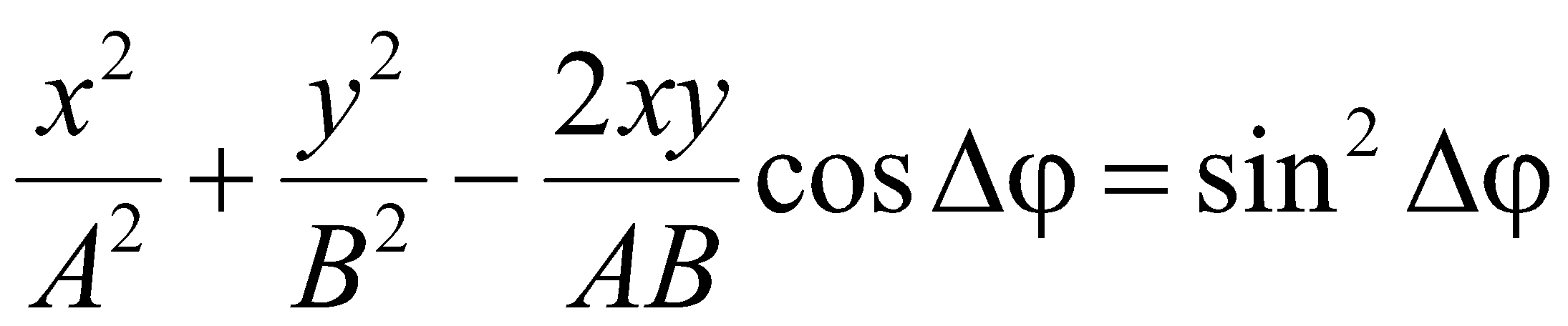 :4 7. [Уд1] (ВО1) Точка М одновременно совершает колебания по гармоническому закону вдоль осей координат ОХ и ОУ с одинаковыми амплитудами, разность фаз равна 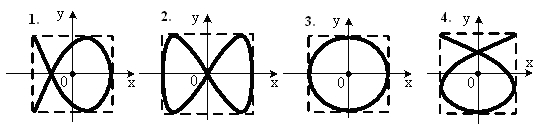 1) 1 2) 2 3) 3 4) 4 :3 8. [Уд1] (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с различными амплитудами, но одинаковыми частотами. При разности фаз π траектория точки имеет вид, соответствующий схеме под номером 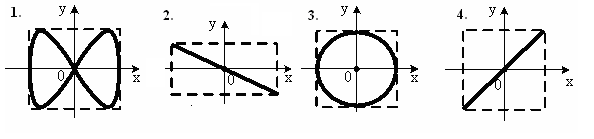 1) 1 2) 2 3) 3 4) 4 :2 9. [Уд1] (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с одинаковыми амплитудами, и одинаковыми частотами. При разности фаз 0 траектория точки имеет вид, соответствующий схеме под номером  1) 1 2) 2 3) 3 4) 4 :4 10. [Уд1] (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с одинаковыми амплитудами, но разными частотами. При разности фаз π/2 траектория точки имеет вид, соответствующий схеме под номером  1) 1 2) 2 3) 3 4) 4 :1 11. [Уд1] (ВО1) Точка М одновременно колеблется по гармоническому закону вдоль оcей координат ОХ и ОУ с одинаковыми амплитудами, разность фаз равна 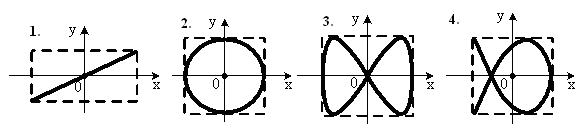 1) 1 2) 2 3) 3 4) 4 :4 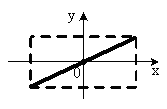 12. [Уд1] (ВО1) При сложении двух взаимно-перпендикулярных колебаний одинаковой частоты траектория результирующего движения материальной точки представлена на рисунке. Тогда разность фаз Δϕ складываемых колебаний равна 1) π 2) 0 3) 3π 4) π/2 :2 13. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1=4 см и А2=3 см. Амплитуда их результирующего колебания Ар=7 см. Разность фаз складываемых колебаний равна 1) ∆φ = 0 2) ∆φ = 3) ∆φ = 4) ∆φ = π :1 14. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Амплитуда их результирующего колебания Ар = 5 см. Разность фаз складываемых колебаний равна 1) ∆φ = 0 2) ∆φ = 3) ∆φ = 4) ∆φ = π :3 15. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Амплитуда их результирующего колебания Ар = 1 см. Разность фаз складываемых колебаний равна 1) ∆φ = 0 2) ∆φ = 3) ∆φ = 4) ∆φ = π :4 16. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Разность фаз складываемых колебаний равна ∆φ = 1) 7 2) 5 3) 1 4) 12 :2 Дисциплина: Физика Тема: 060 Механические колебания и волны V064 – П Волновое движение S064 – П Волновое движение - 10 заданий 1. [Уд1] (ВО1) Решением волнового уравнения 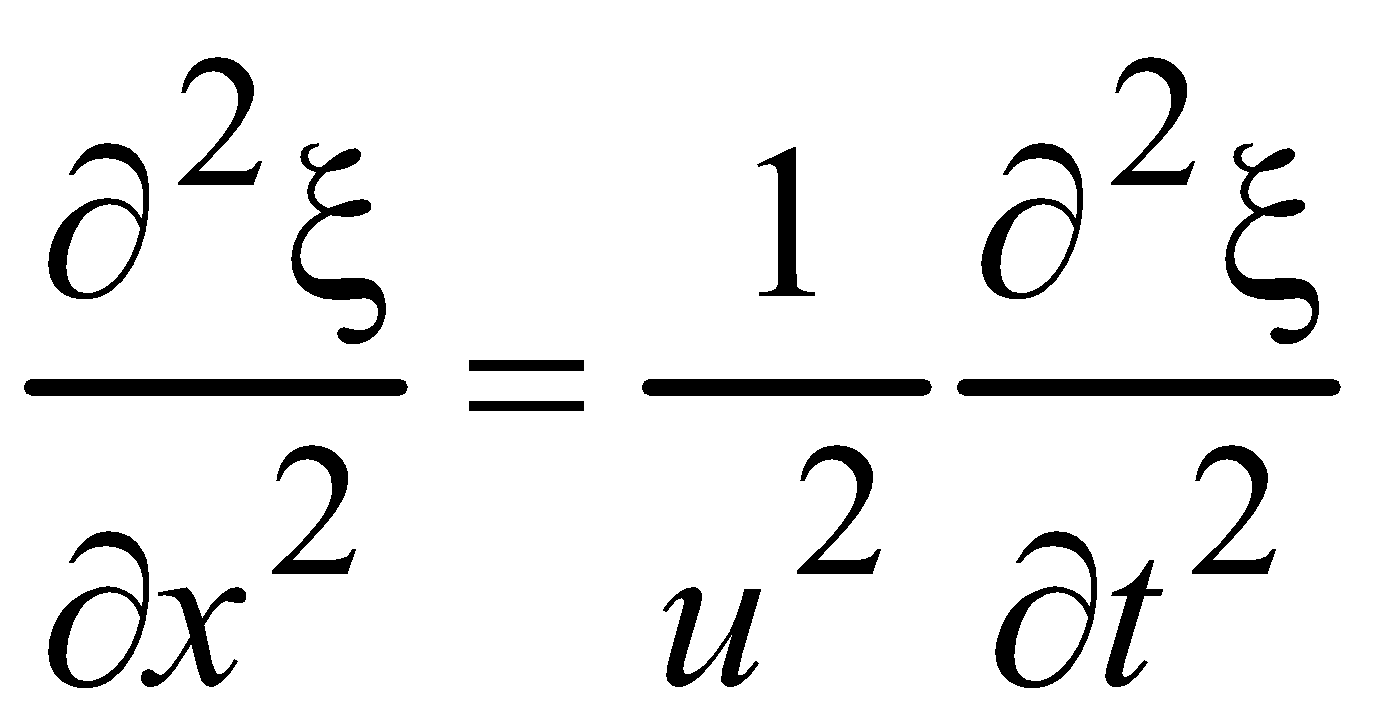 является уравнение плоской монохроматической волны ξ, которая распространяется вдоль направления оси Ох. Это уравнение представлено формулой является уравнение плоской монохроматической волны ξ, которая распространяется вдоль направления оси Ох. Это уравнение представлено формулой 1) 2) 3) 4) :4 2. [Уд1] (ВО1) Уравнение плоской синусоидальной волны, распространяющейся вдоль оси Ох со скоростью v = 500 м/с, имеет вид ξ = 0,01 sin (ωt – 2х). Циклическая частота ω равна … рад·с-1. 1) 1000 2) 159 3) 0,02 4) 0,001 :1 3. [Уд1] (ВО1) Уравнение плоской монохроматической волны ξ, которая распространяется вдоль положительного направления оси Ох представлено формулой 1) 2) 3) 4) :4 4. [Уд1] (ВО1) Уравнение сферической монохроматической волны ξ представлено формулой 1) 2) 3) 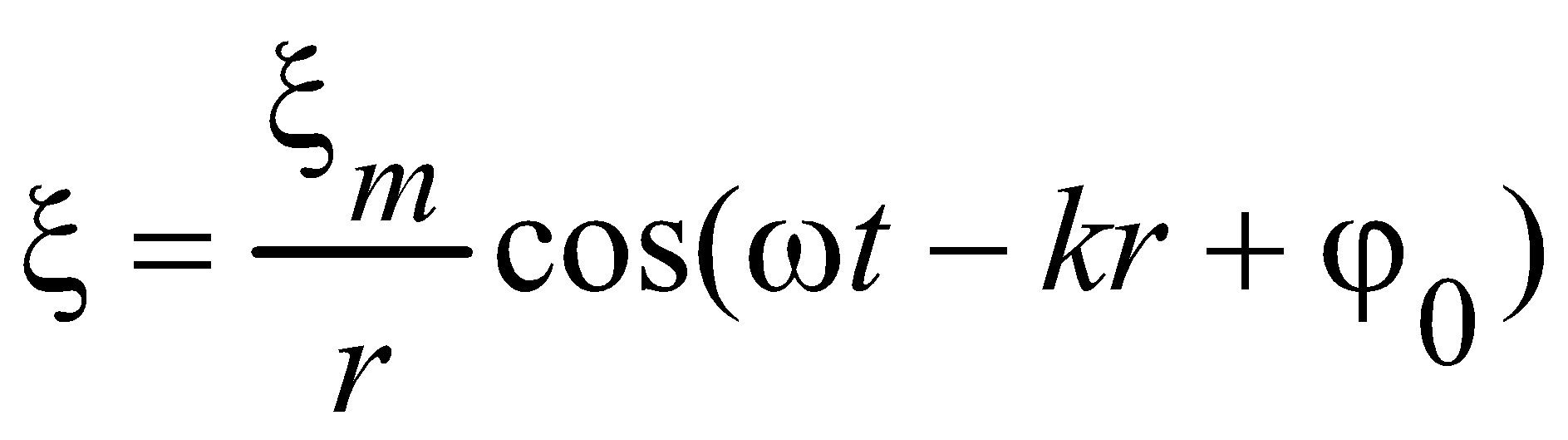 4) :3 5. [Уд1] (ВО1) Уравнение стоячей волны ξ представлено формулой 1) 2) 3) 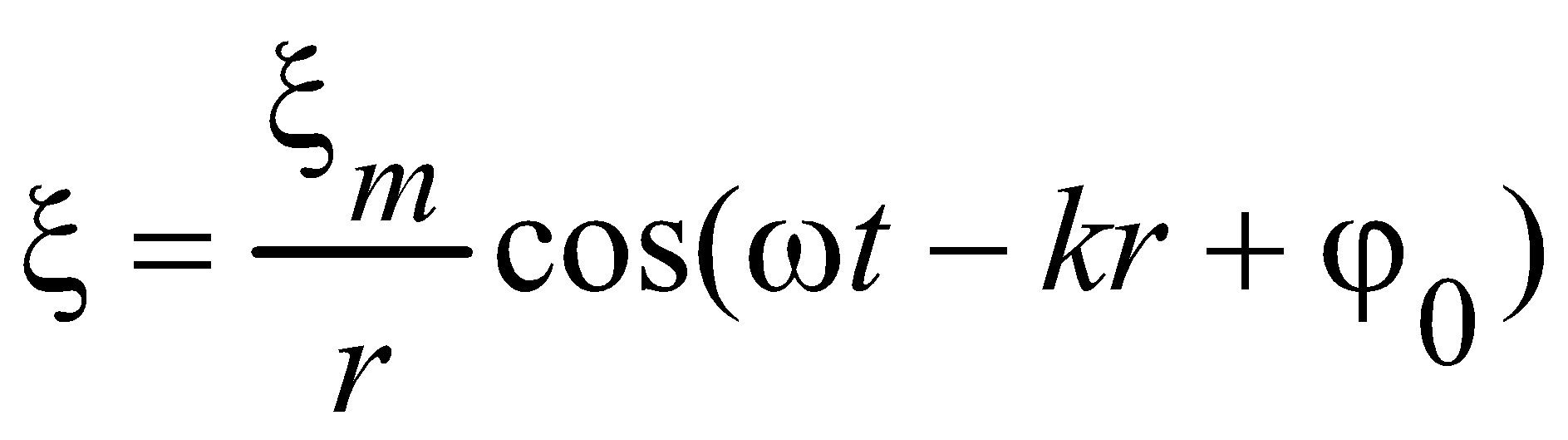 4) :2 6. [Уд1] (ВО1) При интерференции двух волн результирующая волна характеризуется изменением 1) частоты волны 2) длины волны 3) распределения энергии в пространстве 4) периода колебаний :3 7. [Уд1] (ВО1) Источник колебаний, находится в упругой среде, и точки этой среды находятся на расстоянии 1) 2π 2) 0,5π 3) 0,25π 4) 0,33π :2 8. [Уд1] (ВО1) Если разность фаз колебаний источника волн в упругой среде равна 1) 20 2) 30 3) 40 4) 50 :3 9. [Уд1] (О) Точки пространства, в которых амплитуда колебаний стоячей волны, равна нулю, называются … стоячей волны. Узлы, узлами 10. [Уд1] (ВО1) В стоячей волне расстояния между двумя соседними пучностями равно 1) λ 2) λ/2 3) 3λ/2 4) 2λ :2 C064 – П Волновое движение (графики) – 4 задания 1. [Уд1] (ВО1) В упругой среде в положительном направлении оси 0x распространяется плоская волна. На рисунке приведен график зависимости смещения ξ частицы среды от времени t в произвольной точке оси 0х 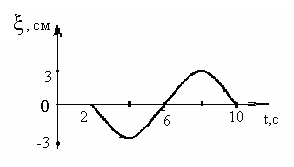 . Циклическая частота волны … рад/c.1) 2π 2) 0,8π 3) π/4 4) π/3 :3 2. [Уд1] (ВО1) В упругой среде в положительном направлении оси 0x распространяется плоская волна. На рисунке приведен график зависимости смещения ξ частицы среды от времени t в произвольной точке оси 0х  . Если длина волны равна 40 м, то скорость распространения составляет … м/c.1) 2 2) 5 3) 8 4) 10 :2 3. [Уд1] (ВО1) На рисунке приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 6 с. Источник колебаний находится в точке с координатой х = 0. В начальный момент времени (t 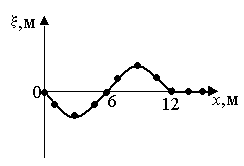 = 0) все частицы среды находились в покое. Фазовая скорость волны равна … м/c.1) 12 2) 6 3) 4 4) 2 :4 4. [Уд1] (ВО1) На рисунке приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 6 с. Источник колебаний находится в точке с координатой х = 0. В начальный момент времени (t  = 0) все частицы среды находились в покое. Циклическая частота волны равна … рад/c.1) 2π 2) 0,8π 3) π/4 4) π/3 :4 Дисциплина: Физика Тема: 240 Электромагнитная индукция |
