рр. 060 Механические колебания и волны
 Скачать 2.05 Mb.
|
|
Не могут быть измерены одновременно в условиях одного опыта сколь угодно точно пары величин, записанные под номерами 1) (λ,v) 2) (х,рУ) 3) (z,рz) 4) (у,рУ) :3, 4 11. [Уд1] (ВОМ) Соотношение неопределенностей для энергии и времени записывается так:  В этом соотношении... 1) ΔW - разность энергий электрона в возбужденном (Wn) и основном (W1) состояниях 2) .. ΔW - неопределенность энергии W электрона 3) . Δt - неопределенность времени жизни электрона в состоянии с энергией W 4).. Δt - промежуток времени, в течение которого происходит переход электрона из основного состояния (W1) в возбужденное (Wn) Верные утверждения о неопределенности энергии и времени приведены под номерами… :2, 3 Дисциплина: Физика Индекс темы 420 «Волновые свойства частиц» Вариация v424 Уравнение Шредингера. Решение квантовомеханических задач Контроль: П - промежуточный П С424 Кластер (Волновая функция. МКЧ в потенциальной яме. Барьер ) 7 заданий 1. [Уд] (ВО1) Квадрат модуля амплитуды волновой функции равен … микрочастицы. 1) плотности вероятности местонахождения 2) вероятности местонахождения 3) плотности энергии 4) импульсу :1 2. [Уд] (ВО1) Если частица находится в основном состоянии в одномерной бесконечно глубокой потенциальной яме, то 1) потенциальная энергия ее внутри ямы отлична от нуля 2) у стенок ямы потенциальная энергия постепенно возрастает от нуля до бесконечности 3) волновая функция равна нулю внутри ямы 4) волновая функция обращается в нуль на границах потенциальной ямы : 4 3. [Уд] (ВО1) Ошибочное утверждение об энергии частицы в бесконечно глубокой потенциальной яме – 1) энергетический спектр частицы в яме является дискретным 2) интервал между соседними энергетическими уровнями растет с увеличением энергии частицы 3) интервал между соседними энергетическими уровнями уменьшается с увеличением энергии частицы 4) интервал между соседними энергетическими уровнями зависит от квантового числа :3 4. [Уд] (ВО1) Вероятность прохождения микрочастицы с энергией W через высокий потенциальный барьер конечной ширины d зависит от … частицы. 1) заряда 2) массы 3) собственного магнитного момента 4) собственного момента импульса :2 5. [Уд] (ВО1) Вероятность прохождения микрочастицы через потенциальный барьер, высота U0 которого больше полной энергии W  частицы не зависит от1) массы m частицы 2) энергии W частицы 3) спина  частицы4) ширины d потенциального барьера 5) высоты U0 потенциального барьера :3 6. [Уд] (ВОМ) Уравнение Шредингера для стационарных состояний в однородном случае имеет вид: 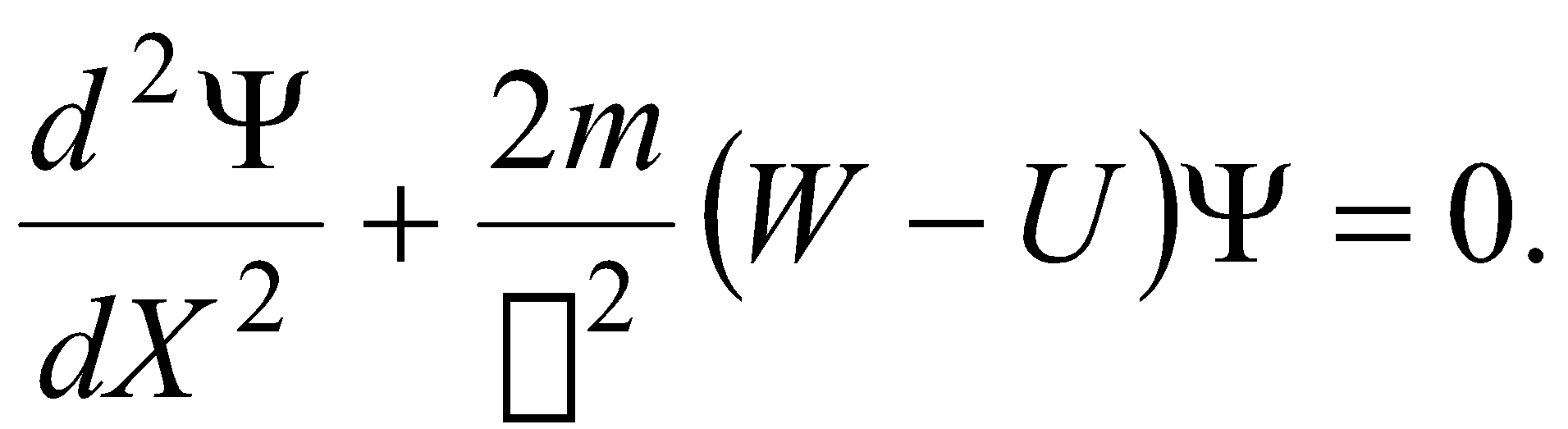 Верные утверждения: 1) в этом уравнении  .– волновая функция, зависящая от координаты Х и времени t2) m – масса частицы 3) W – полная энергия частицы 4) (W – U) – кинетическая энергия частицы : 2, 3, 4 7. [Уд] (ВОМ) Решение уравнения Шредингера для стационарных состояний частицы в бесконечно глубокой одномерной потенциальной яме шириной l имеет вид:  , где  .Число n в этом уравнении 1) определяет возможные значения длин волн де Бройля частицы в яме 2) определяет возможные значения энергии частицы в яме 3) может принимать значение n = 0 4) определяет вероятность обнаружить частицу в различных частях ямы :1, 2, 4 Контроль: П - промежуточный П S424 Сингл ( ) 12 заданий 1. [Уд] (ВО1) Для свободной микрочастицы неверным является утверждение, что у нее … 1) энергия квантована 2) потенциальная энергия равна нулю 3) длина волны де Бройля может иметь любые значения 4) импульс может принимать любые значения :1 2. [Уд] (ВО1) Плотность вероятности обнаружения свободной микрочастицы 1) одинакова во всех точка пространства 2) уменьшается при удалении от частицы 3) возрастает при удалении от частицы 4) не определена в данный момент времени :1 3. [Уд] (ВО1) Микрочастица находится в одномерной прямоугольной бесконечно глубокой потенциальной яме конечной ширины. Энергетический спектр этой частицы 1) сплошной 2) дискретный, сходящийся 3) дискретный, расходящийся 4) дискретный, эквидистантный :3 4. [Уд] (ВОМ) Для микрочастицы, находящейся в бесконечно глубокой потенциальной яме, главное квантовое число n 1) может принимать любые значения 2) определяет возможные значения энергии частицы в яме 3) может принимать целочисленные значения, начиная с n =0 4) определяет вероятность обнаружить частицу в различных интервалах ямы :2,4 5. [Уд] (ВО1) Волновая функция частицы в потенциальной яме с бесконечно высокими стенками шириной L имеет вид: Ψ =  . Величина импульса этой частицы в основном состоянии равна1)  2)  3)  4)  : 4 6. [Уд] (ВО1) Если электрон находится в потенциальной яме с бесконечно высокими стенками, то 1) вероятность обнаружить электрон у стенок ямы равна нулю 2) длина волны де Бройля может иметь любое значение 3) энергетический спектр электрона дискретный, сходящийся 4) волновая функция убывает по экспоненциальному закону вне ямы : 1 7. [Уд] (О) На рисунке изображены графики волновых функций для различных состояний частицы в бесконечно глубокой потенциальной яме шириной l. Частица обладает наибольшей энергией в случае … :4 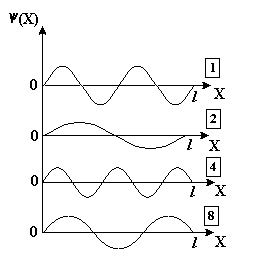 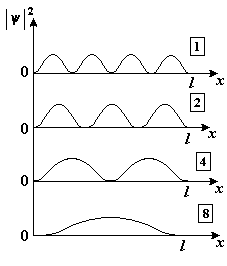 8. [Уд] (О) На рисунке изображены графики плотности вероятности обнаружить частицу на различных расстояниях от стенок бесконечно глубокой одномерной потенциальной ямы шириной l. Микрочастица имеет наибольший импульс в случае …:1 9. [Уд] (ВО1) На рисунках изображены прямоугольные потенциальные барьеры различной ширины d и высоты U0 (на всех рисунках масштабы вдоль осей одинаковы). В направлении потенциального барьера параллельно оси Ох движется частица с энергией W, причем W<U0. Вероятность туннельного эффекта наибольшая в случае 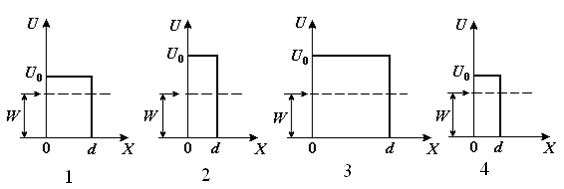 1) 1 2) 2 3) 3 4) 4 :4 10. [Уд] (ВО1) Движущаяся микрочастица с энергией W встречает на своем пути прямоугольный потенциальный барьер ширины d и высоты U0 (U0>W ). При увеличении ширины потенциального барьера вероятность проникновения микрочастицы сквозь барьер (коэффициент прозрачности) 1) увеличится 2) уменьшится 3) не изменится :2 11. [Уд] (ВО1) На рисунке изображена плотность вероятности обнаружения микрочастицы на различных расстояниях от «стенок» ямы. Вероятность её обнаружения на участке 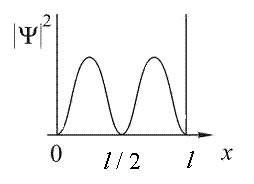  равна1)  2)  3)  4)  :2 |