|
|
ГЛ1. 1 тарау. Жиындар теориясыны элементтері жиыны жиыныны жиыншасы болан жадайда жиыны жиынын амтиды
3 – ескерту. Ашық та емес, тұйық та емес жиындар бар. Мәселен, 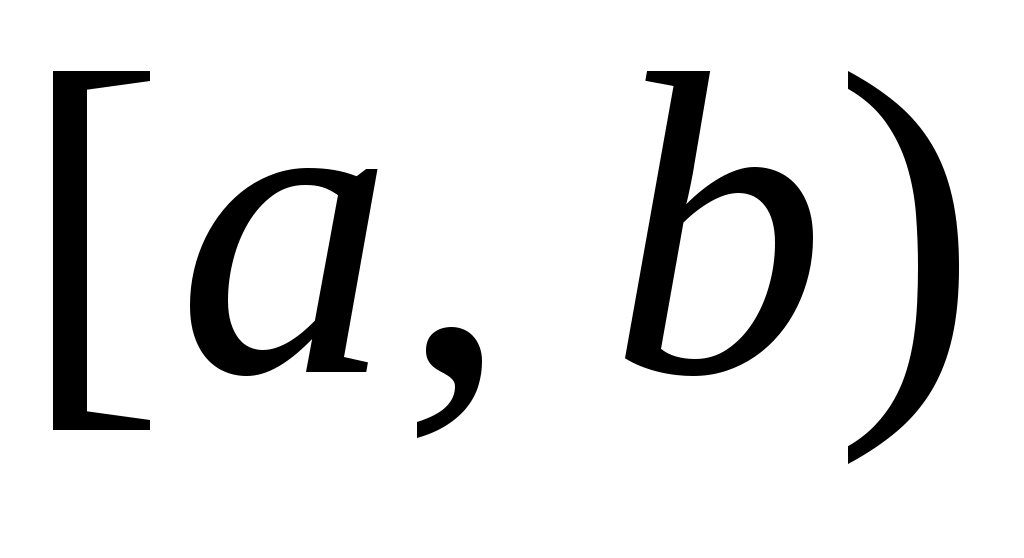 аралығы – ашық жиын да, тұйық жиын да емес. аралығы – ашық жиын да, тұйық жиын да емес.
5 – теорема. Егер 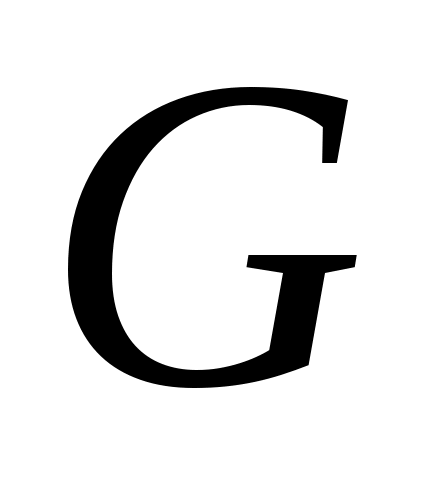 ашық жиын болса, онда ашық жиын болса, онда 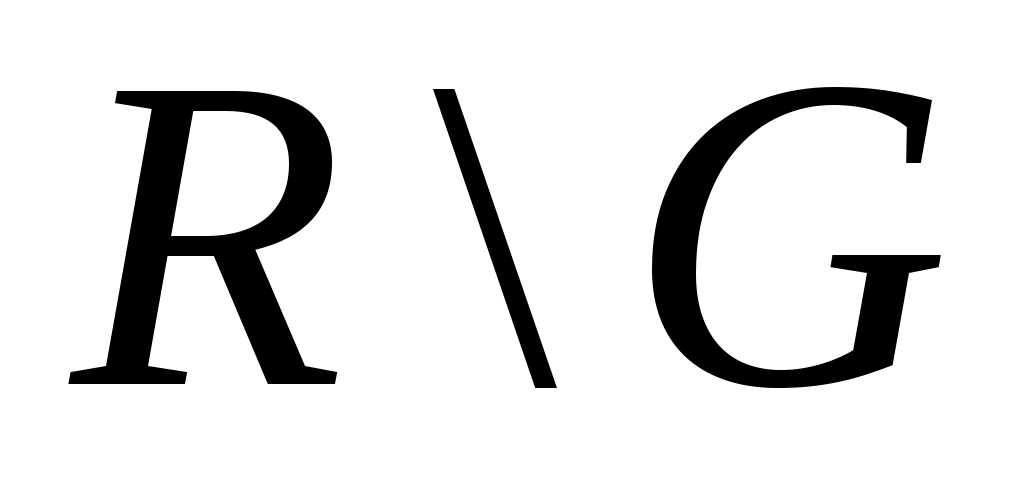 жиыны тұйық жиын болады. жиыны тұйық жиын болады.
Дәлелдеуі. Кері жорысақ, 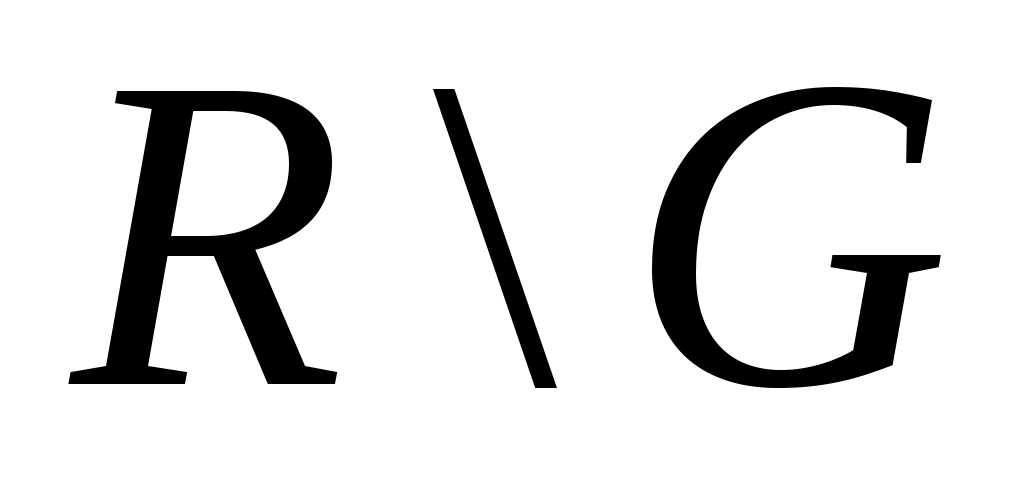 жиынының жиынының 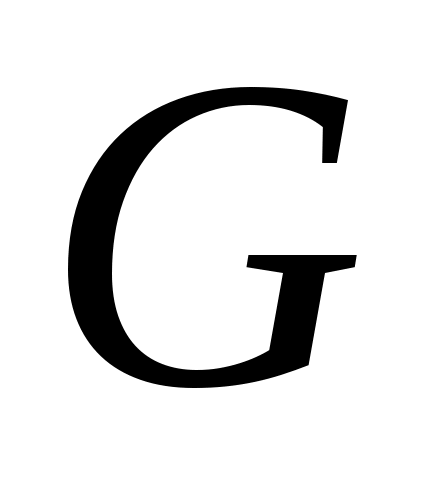 жиынында жататын шектік нүктесі бар болады. Сол нүктені жиынында жататын шектік нүктесі бар болады. Сол нүктені 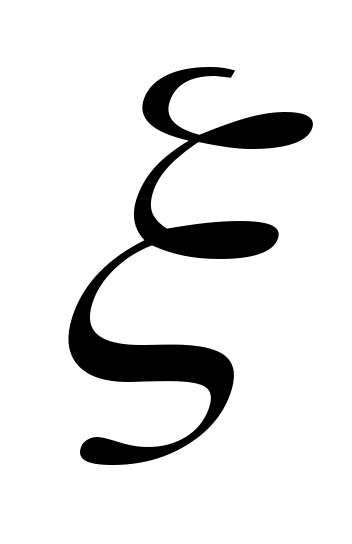 арқылы белгілейік. арқылы белгілейік. 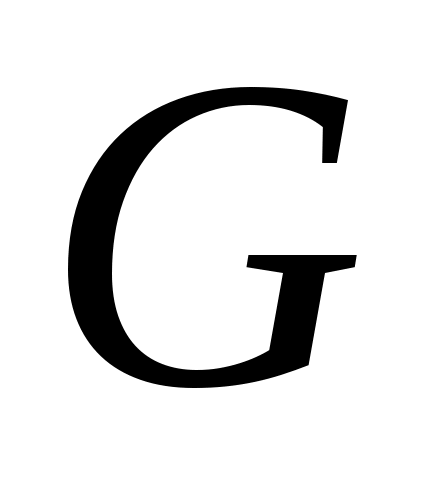 жиынының кез келген нүктесі ішкі нүкте екенін ескерсек, жиынының кез келген нүктесі ішкі нүкте екенін ескерсек, 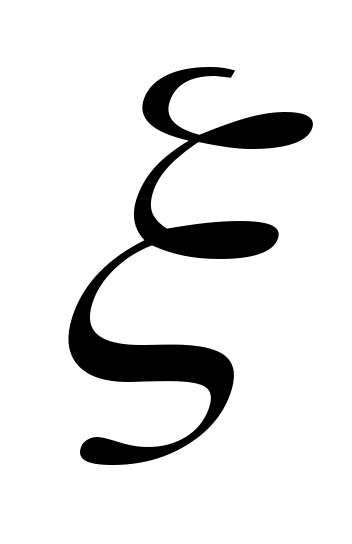 нүктесінің қайсыбір нүктесінің қайсыбір 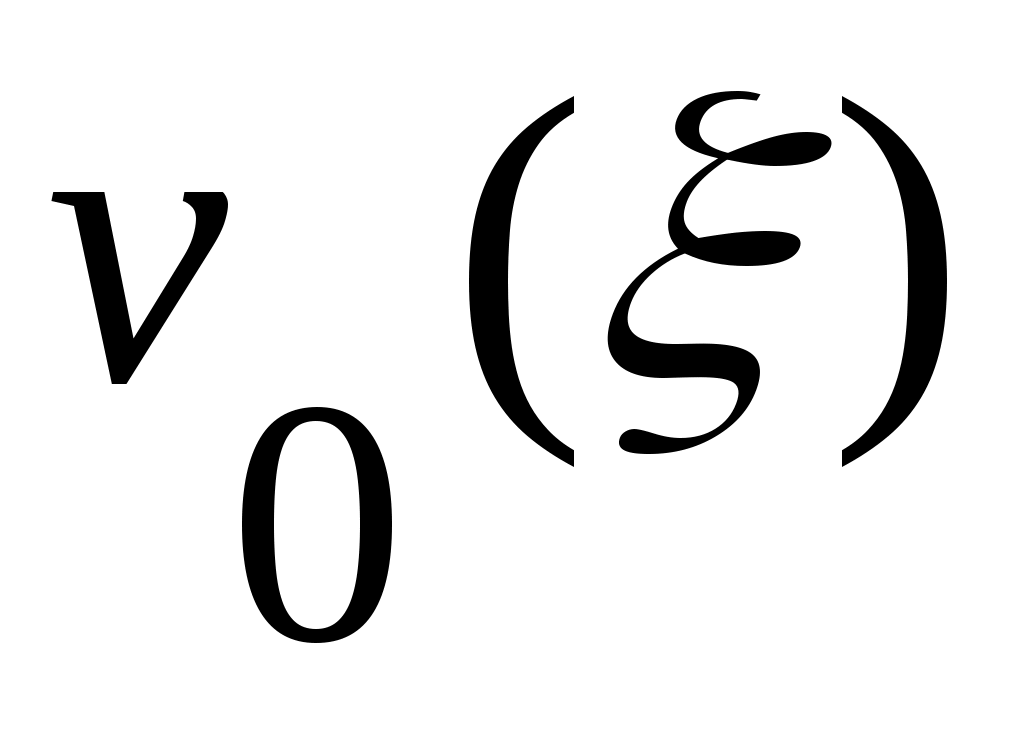 маңайы маңайы 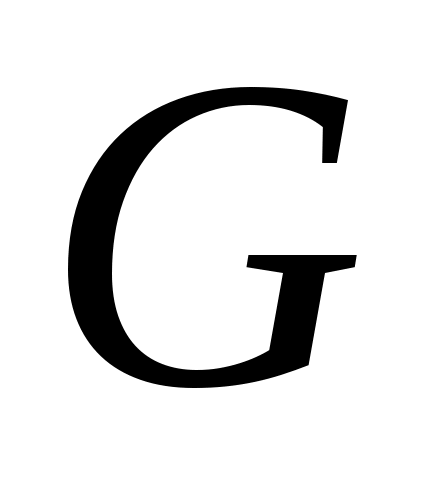 жиынының жиыншасы болады. Демек, жиынының жиыншасы болады. Демек, 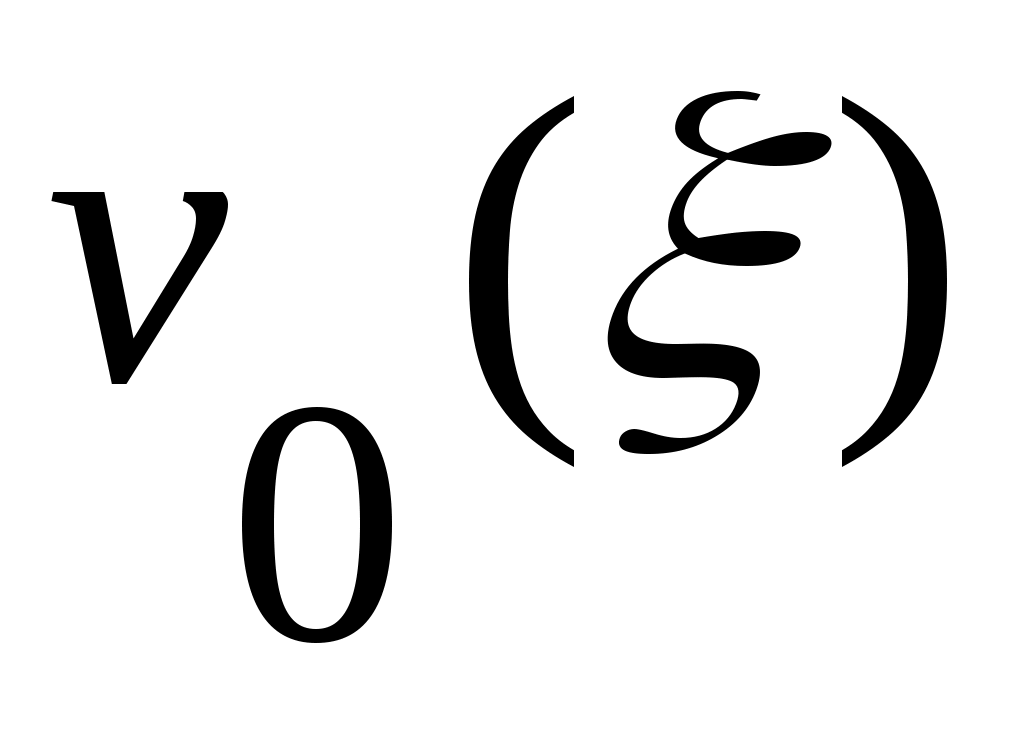 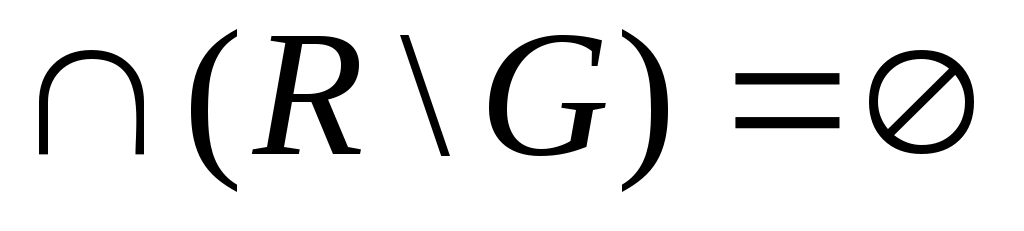 теңдігі орындалады. Бұл теңдік теңдігі орындалады. Бұл теңдік 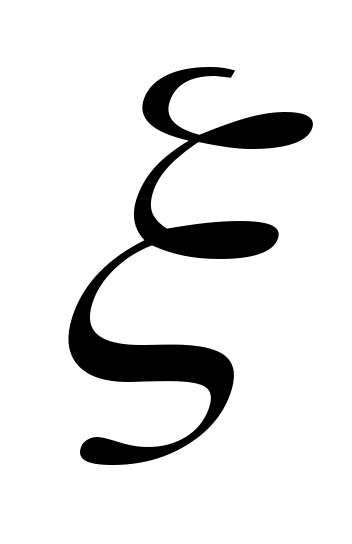 нүктесінің нүктесінің 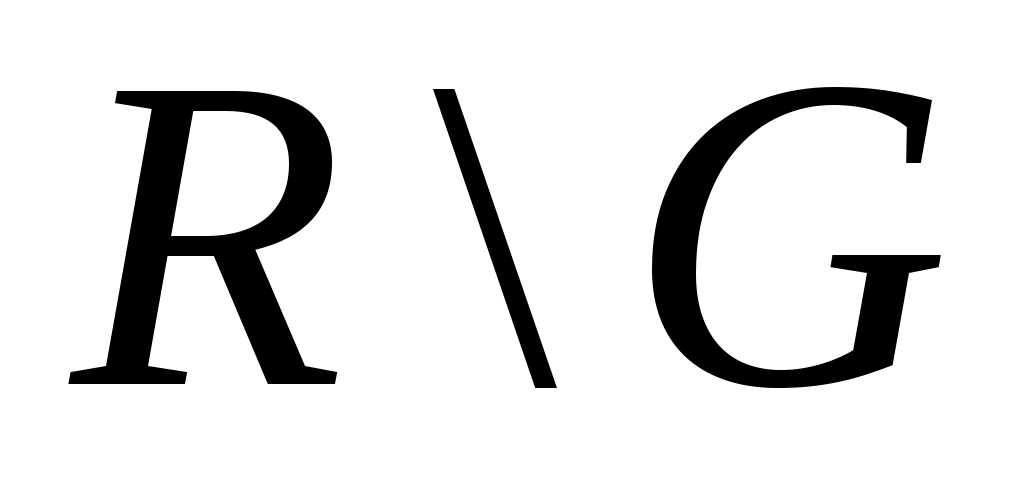 жиынының шектік нүктесі екеніне қайшы. Ендеше, жиынының шектік нүктесі екеніне қайшы. Ендеше, 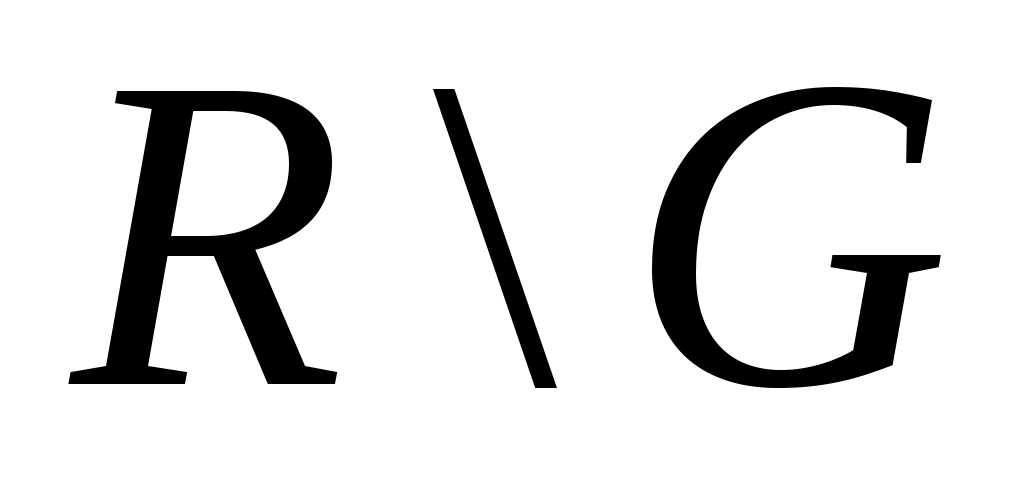 жиыны – тұйық жиын. жиыны – тұйық жиын.
5 – теореманы былай да айтуға болады: ашық жиынның толықтауышы – тұйық жиын.
6 – теорема. Егер 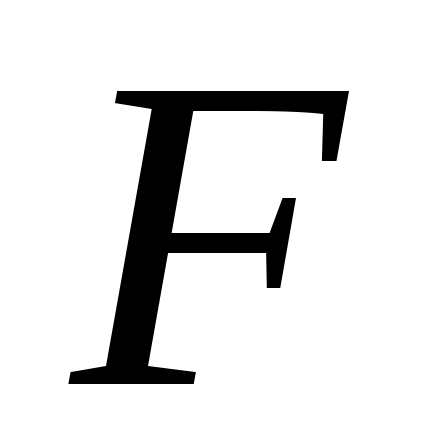 тұйық жиын болса, онда тұйық жиын болса, онда 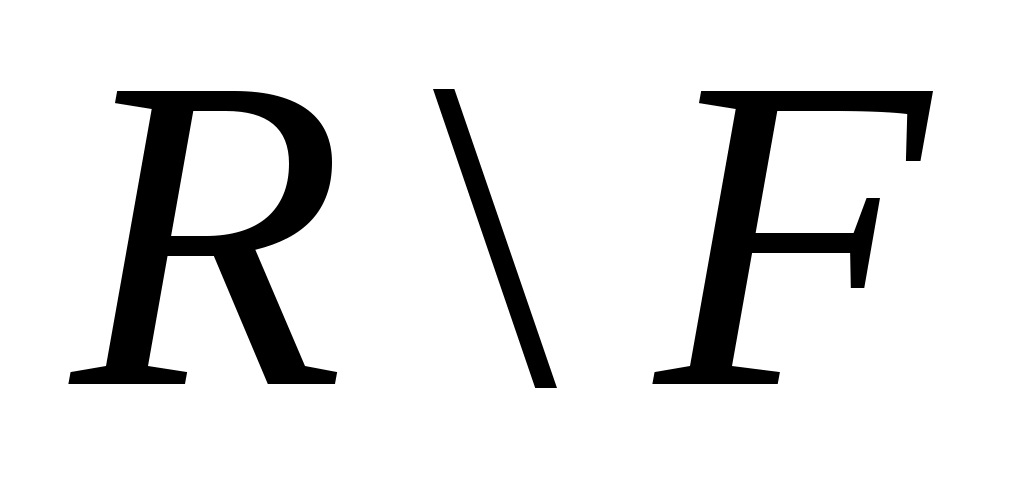 жиыны ашық жиын болады. жиыны ашық жиын болады.
Дәлелдеуі. Егер 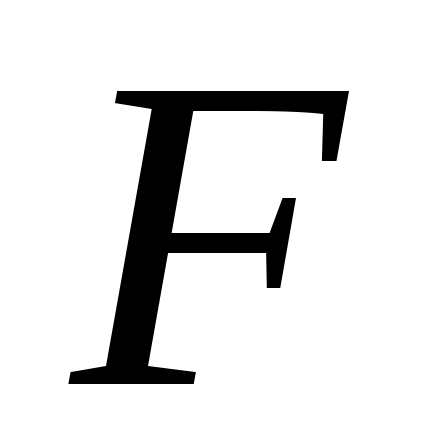 жиыны тұйық болса, онда жиыны тұйық болса, онда 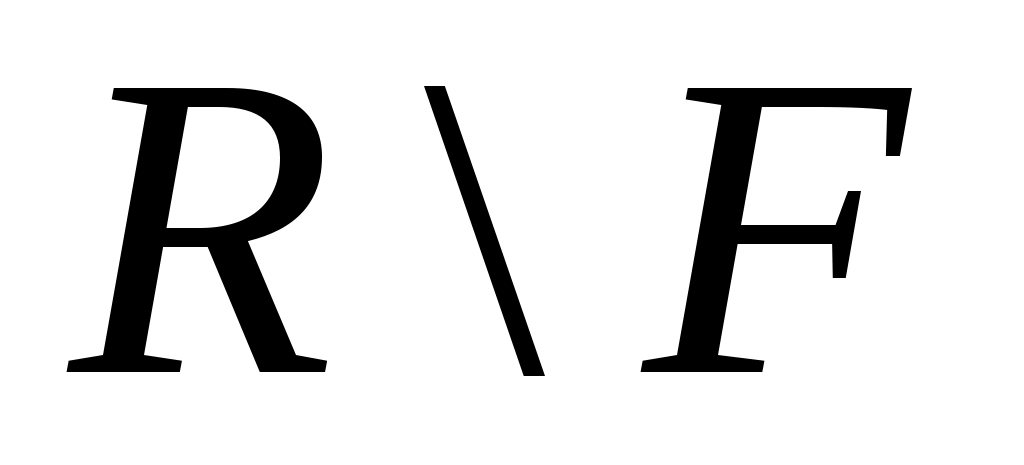 жиынының әрбір нүктесі жиынының әрбір нүктесі 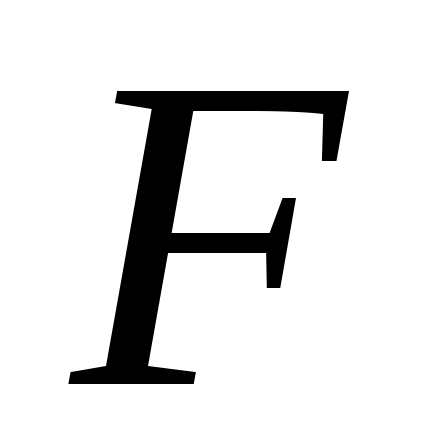 жиынының шектік нүктесі болмайды. Демек, жиынының шектік нүктесі болмайды. Демек, 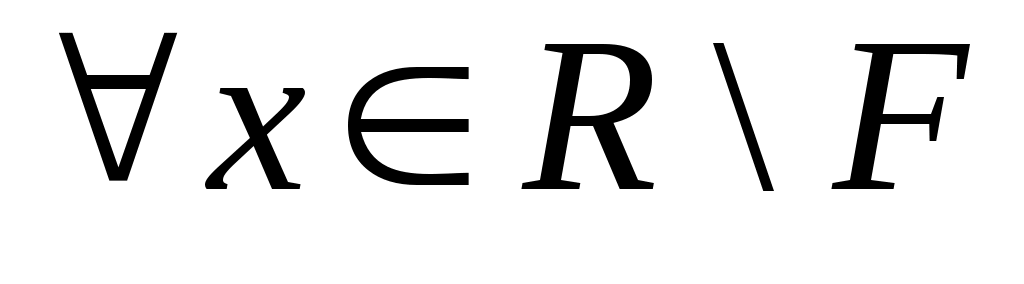 нүктесінің нүктесінің 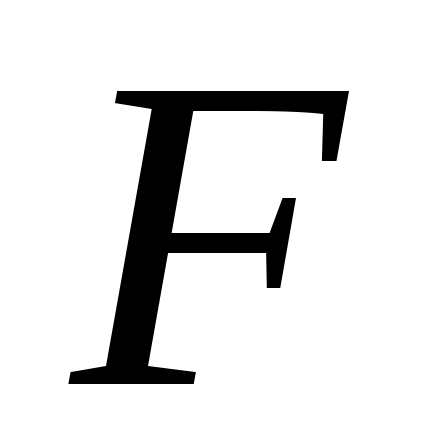 жиынымен қиылыспайтын қайсыбір жиынымен қиылыспайтын қайсыбір 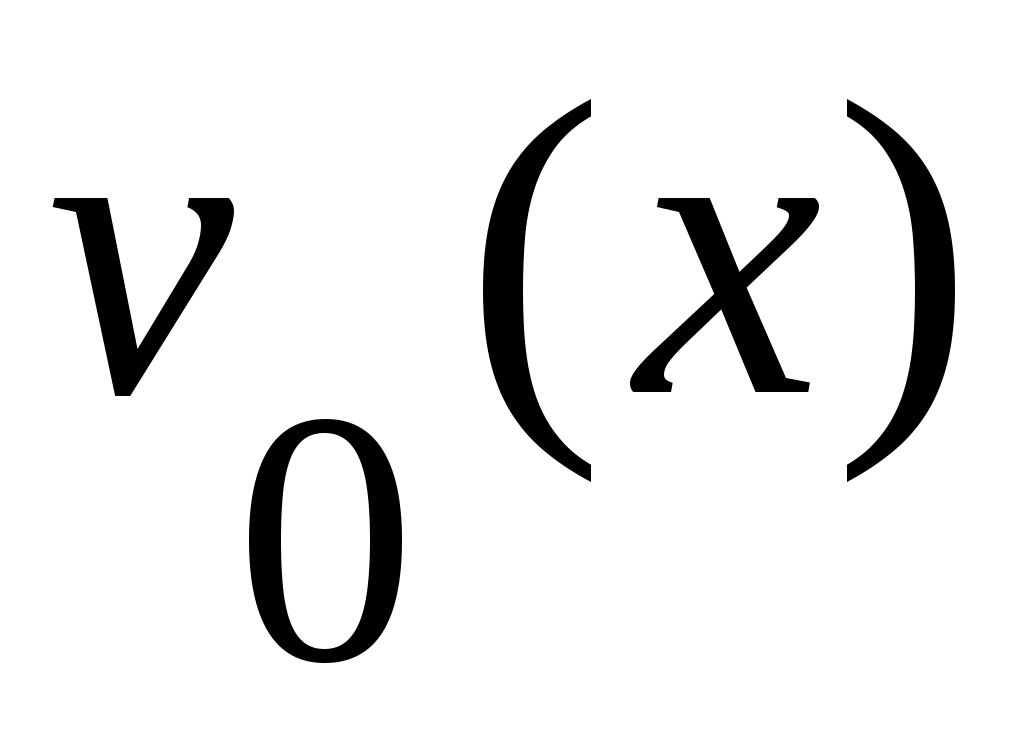 маңайы бар болады, яғни, маңайы бар болады, яғни, 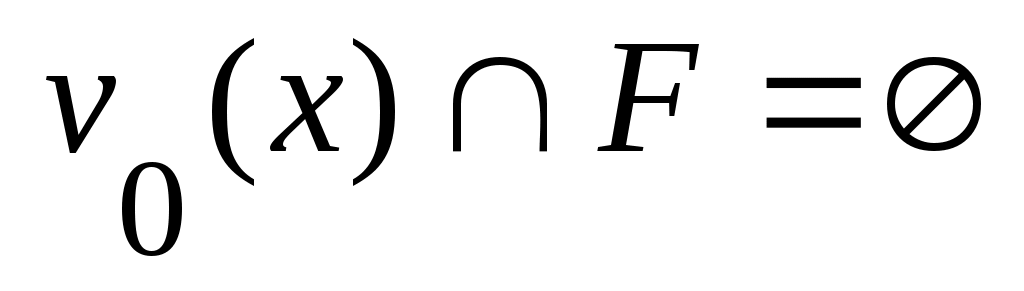 . Бұл теңдік бойынша . Бұл теңдік бойынша 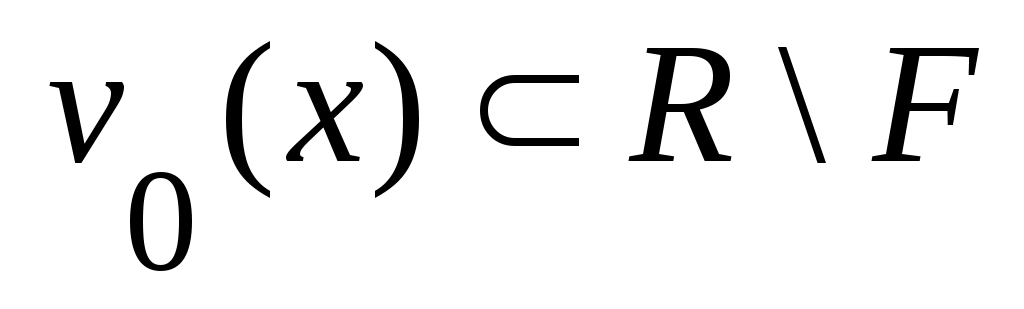 . Сонымен, . Сонымен, 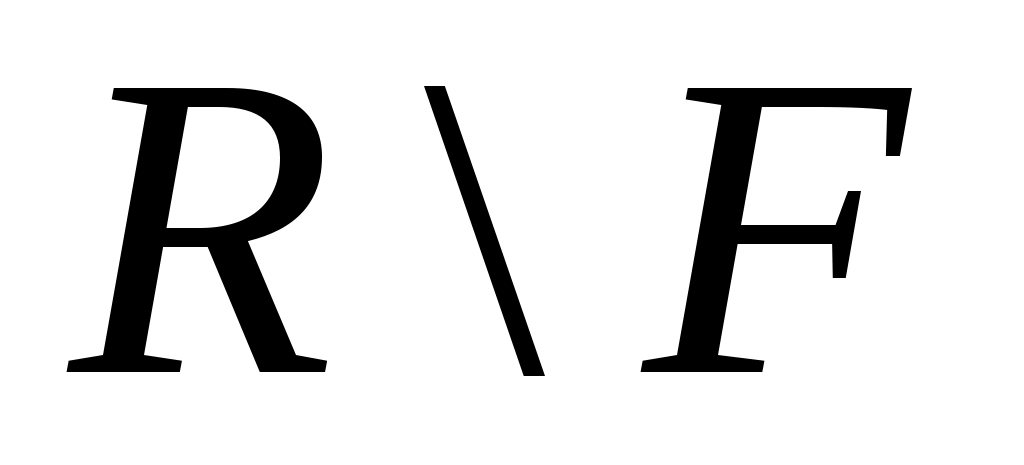 жиынының әрбір нүктесінің ішкі нүкте екеніне көз жеткіздік. Ендеше, жиынының әрбір нүктесінің ішкі нүкте екеніне көз жеткіздік. Ендеше, 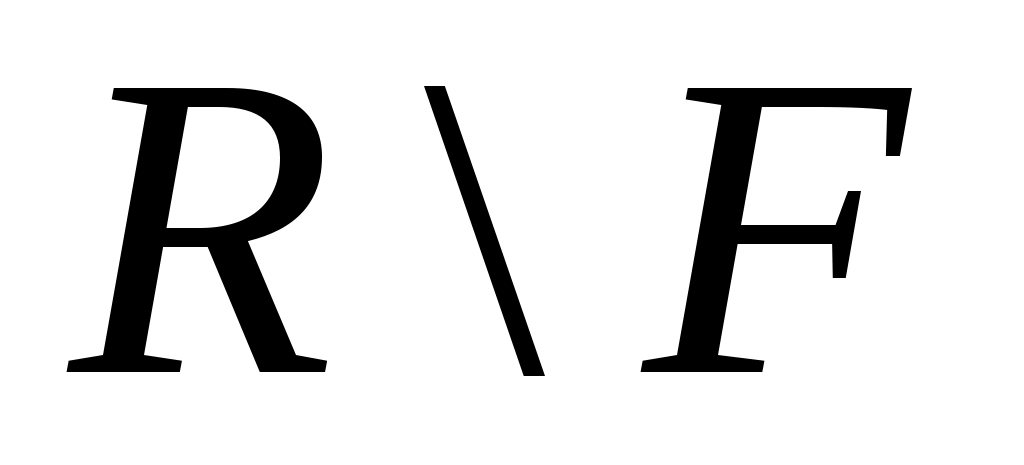 жиыны – ашық жиын. жиыны – ашық жиын.
6 – теореманы былай да айтуға болады: тұйық жиынның толықтауышы – ашық жиын.
4 – ескерту. 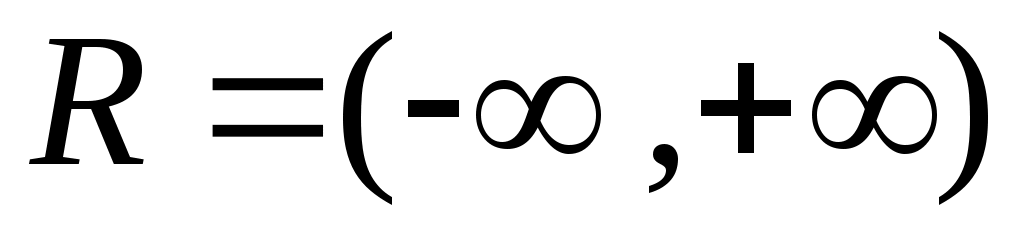 жиыны, бос жиын – әрі ашық, әрі тұйық жиындар (жоғарыдағы мысалдарды, 5 – ші , 6 – шы теоремаларды қараңыз). жиыны, бос жиын – әрі ашық, әрі тұйық жиындар (жоғарыдағы мысалдарды, 5 – ші , 6 – шы теоремаларды қараңыз).
7 – теорема. а) Ашық 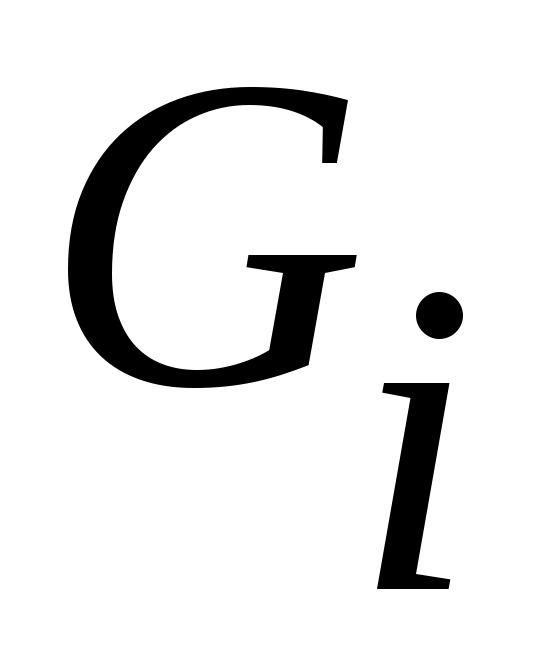 жиындарының ақырлы бірігуі де, саналымды бірігуі де – ашық жиын; ә) Ашық жиындарының ақырлы бірігуі де, саналымды бірігуі де – ашық жиын; ә) Ашық 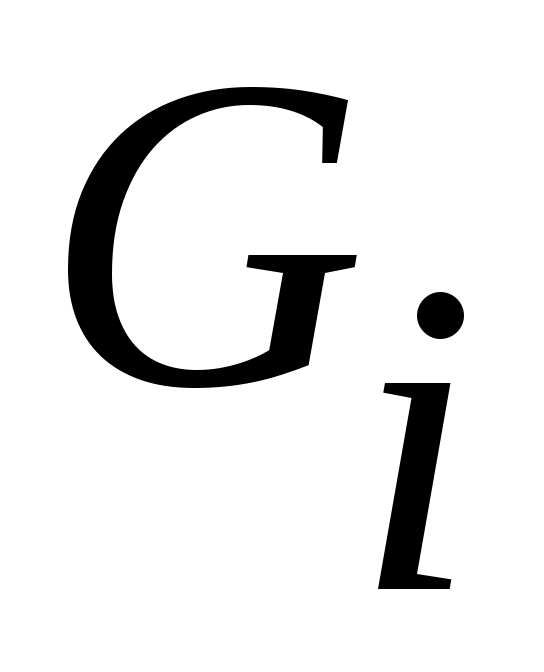 жиындарының ақырлы қиылысуы – ашық жиын. жиындарының ақырлы қиылысуы – ашық жиын.
Дәлелдеуі. а) жағдайында жиындардың бірігуі мен ашық жиын анықтамаларын қолданамыз. ә) жағдайын қарастырайық. 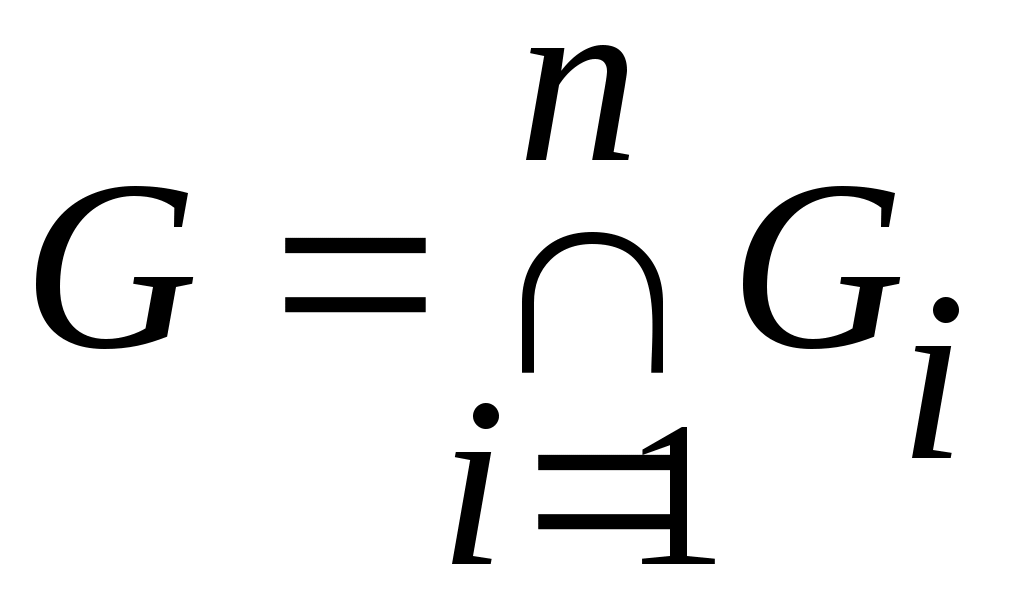 болсын. Кез келген болсын. Кез келген 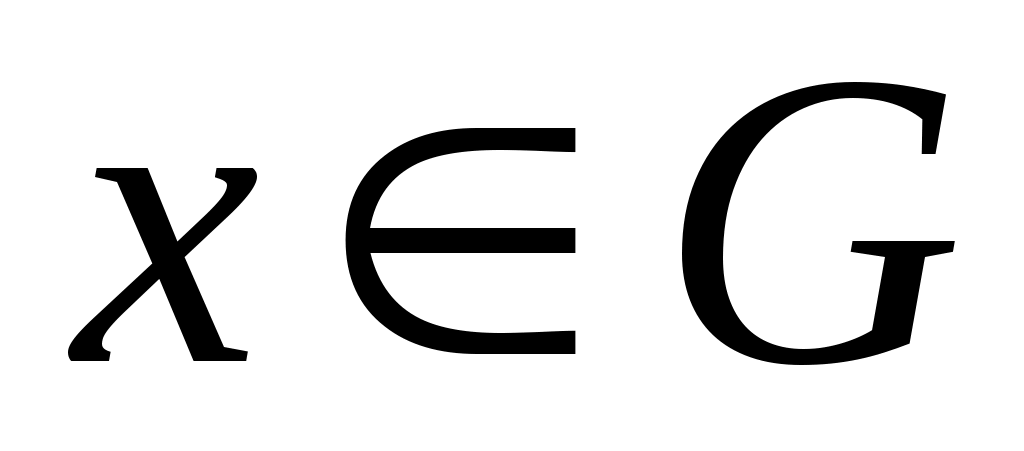 элементі ашық элементі ашық  жиындарында жататындықтан, жиындарында жататындықтан, 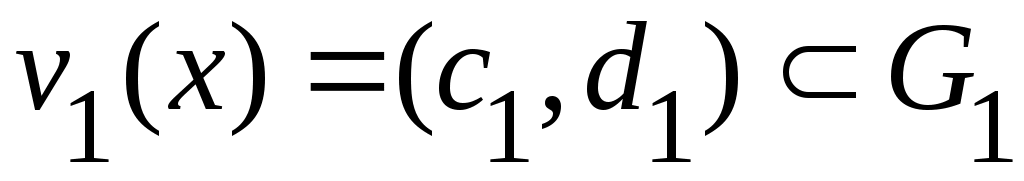 , , 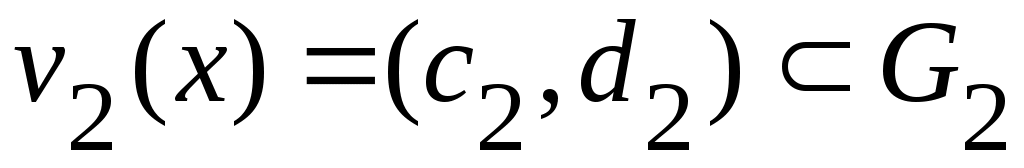 ,..., ,..., 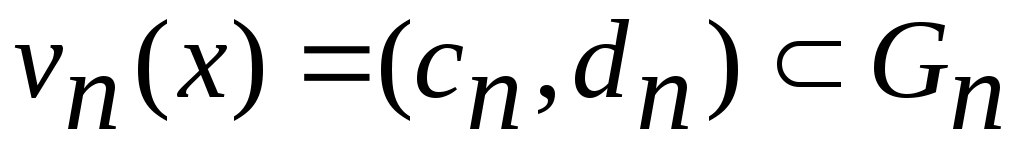 шарттарын қанағаттандыратын шарттарын қанағаттандыратын 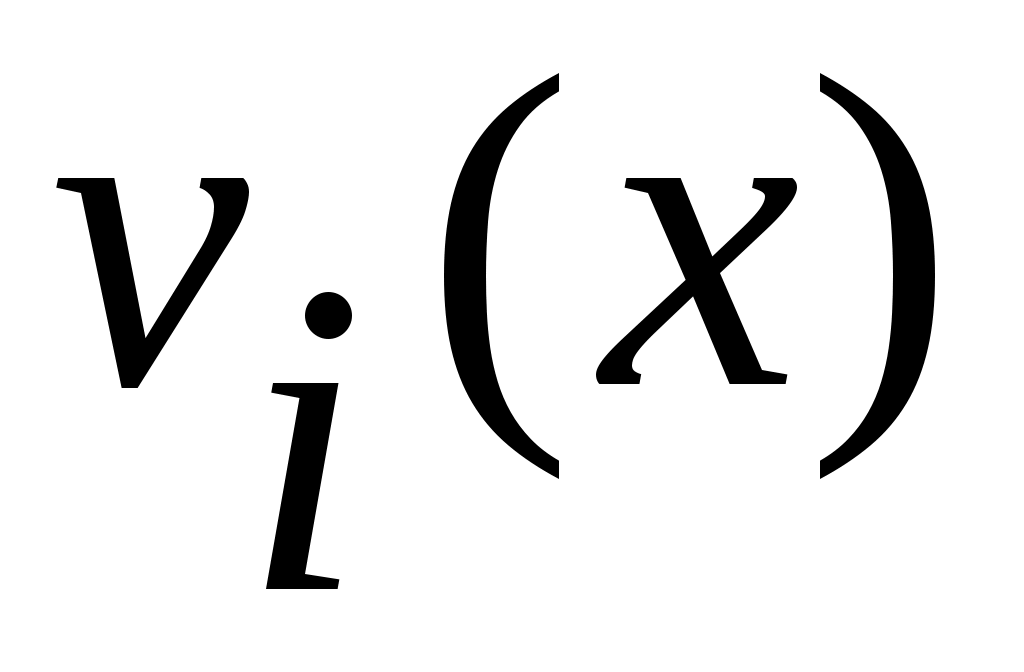 маңайлары табылады. Ал маңайлары табылады. Ал
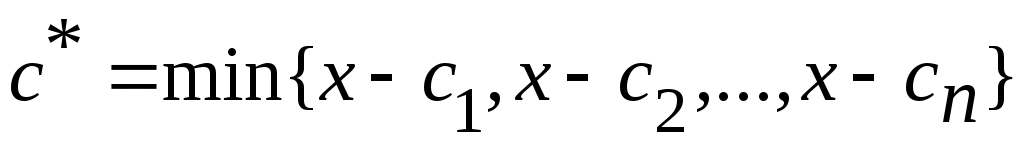 , , 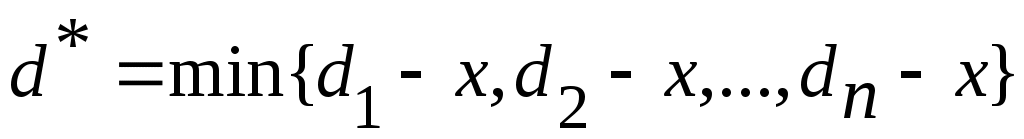
сандары бойынша анықталған 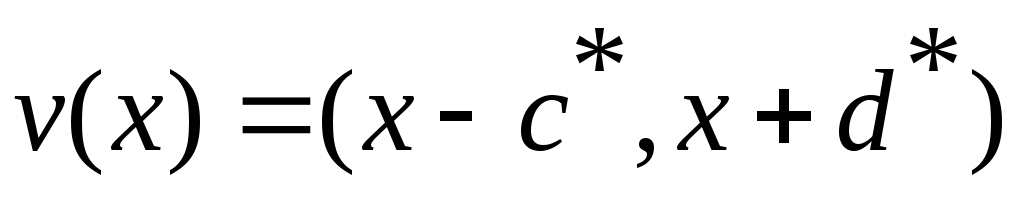 интервалы интервалы  жиынымен қамтылады. Ендеше, жиынымен қамтылады. Ендеше,  жиыны – ашық жиын. жиыны – ашық жиын.
5 – ескерту. Ашық жиындардың саналымды қиылысуы ашық жиын бола бермейді. Мысалы, 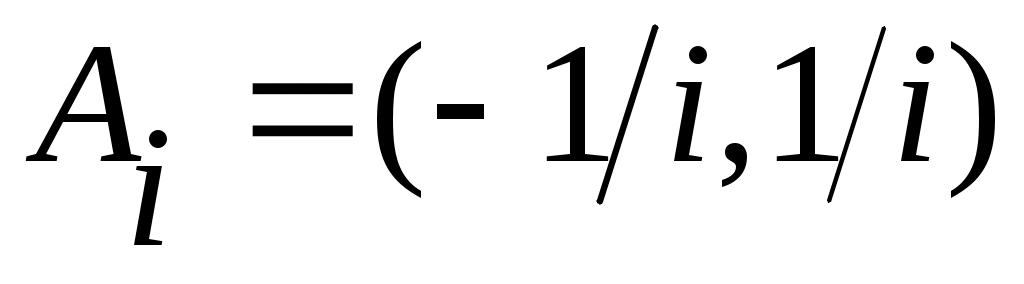 жиындары үшін жиындары үшін 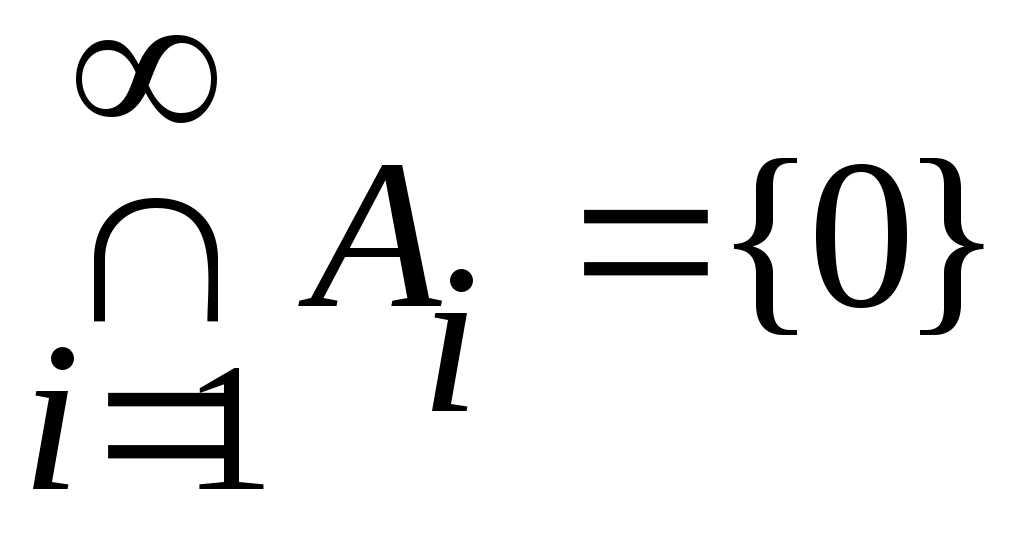 . Ал бір элементті . Ал бір элементті 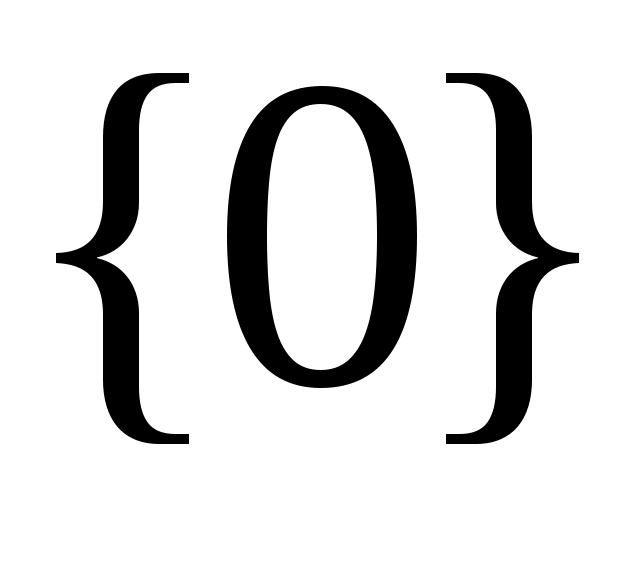 жиыны – тұйық жиын. жиыны – тұйық жиын.
(5 – 7) – теоремалар мен 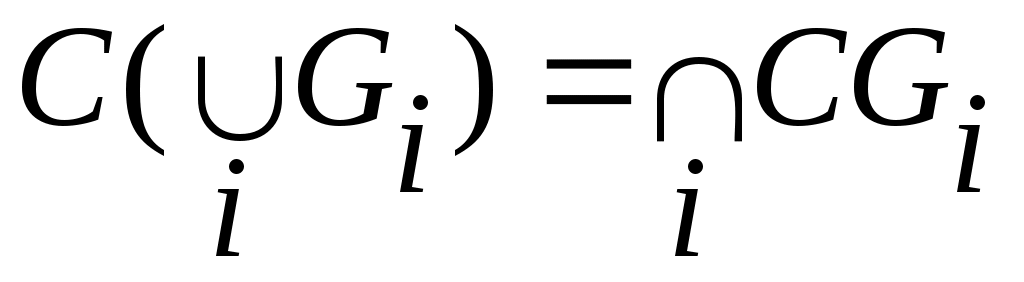 , , 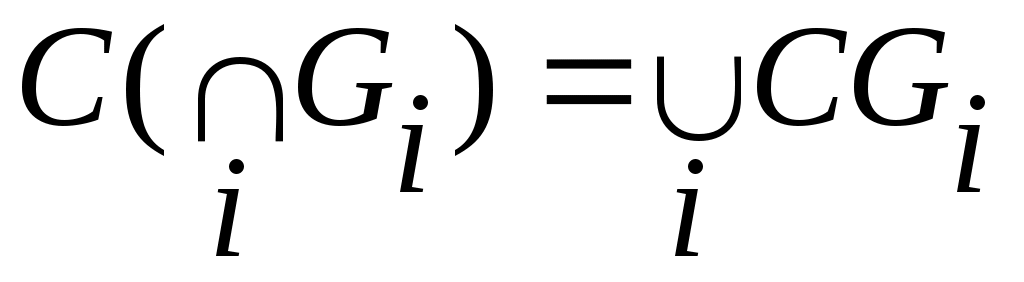 теңдіктерінен мына теореманы аламыз: теңдіктерінен мына теореманы аламыз:
8 – теорема. а) Тұйық жиындардың ақырлы қиылысуы да, саналымды қиылысуы да – тұйық жиын; ә) Тұйық жиындардың ақырлы бірігуі – тұйық жиын.
Келесі теоремада 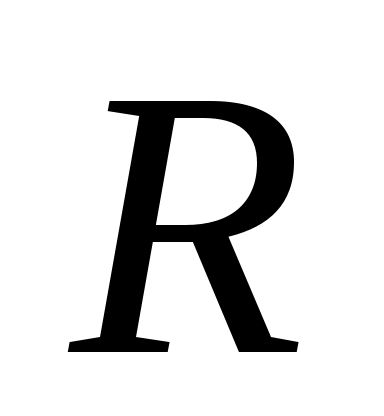 – дегі ашық жиынның құрылымы беріледі. – дегі ашық жиынның құрылымы беріледі.
9 – теорема. Әрбір ашық жиын өзара қиылыспайтын қайсыбір интервалдардың ақырлы немесе саналымды бірігуі болады.
Дәлелдеуі. Ашық 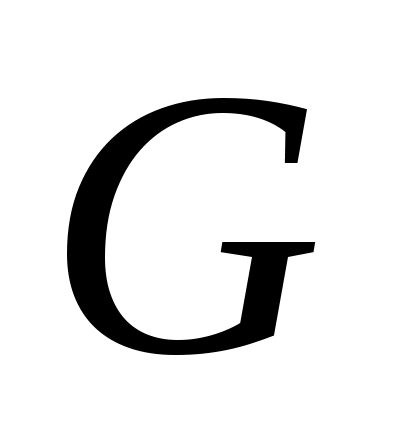 жиыны берілсін. жиыны берілсін. 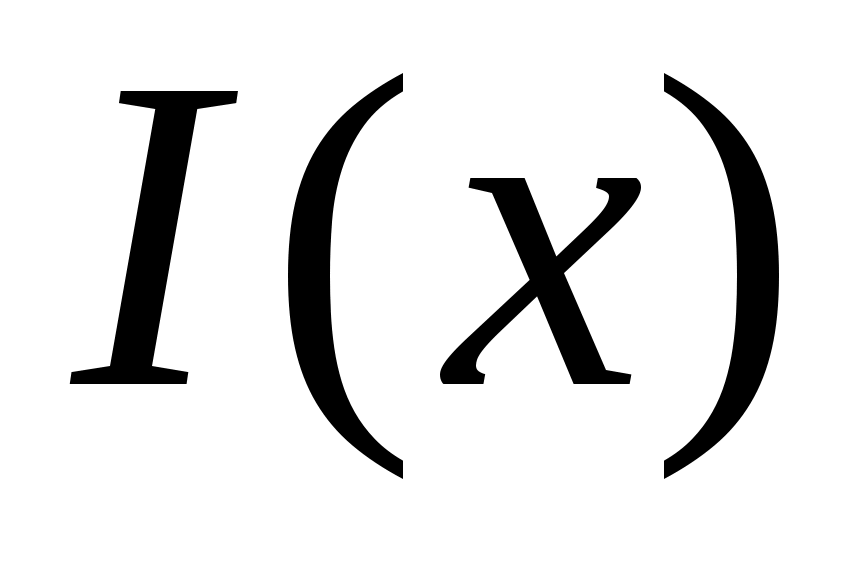 арқылы арқылы 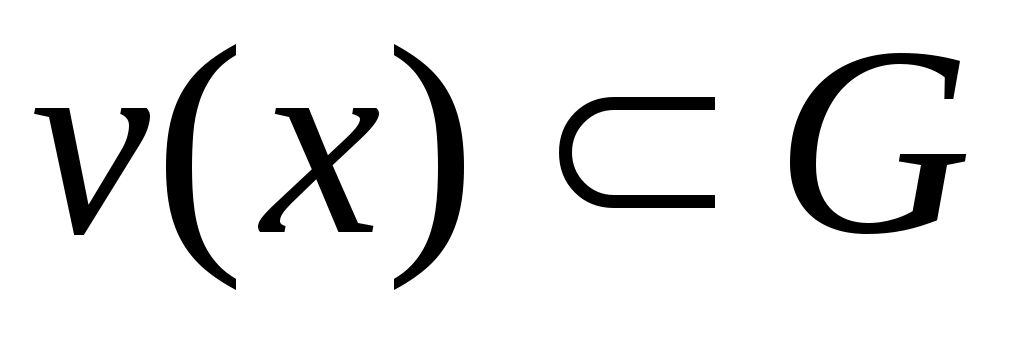 кірістіруін қанағаттандыратын барлық кірістіруін қанағаттандыратын барлық 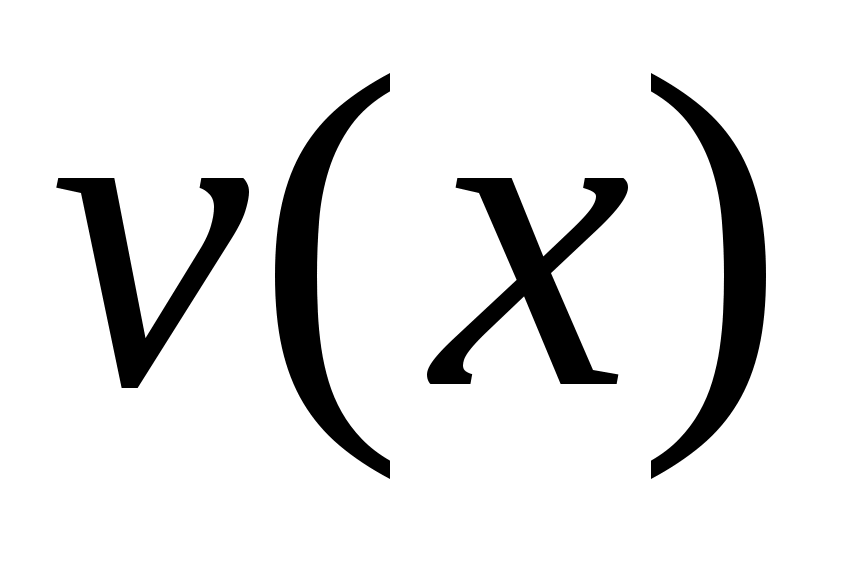 маңайларының бірігуін белгілейік. Ұштары маңайларының бірігуін белгілейік. Ұштары 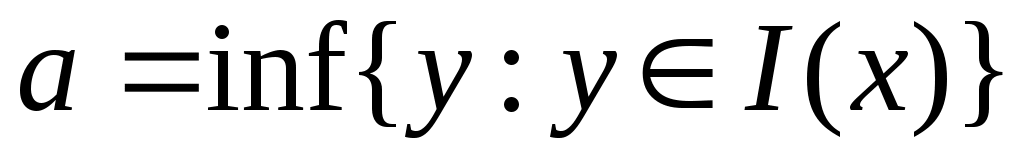 , ,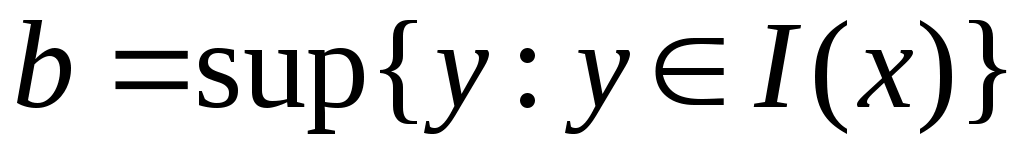 теңдіктері бойынша анықталған теңдіктері бойынша анықталған 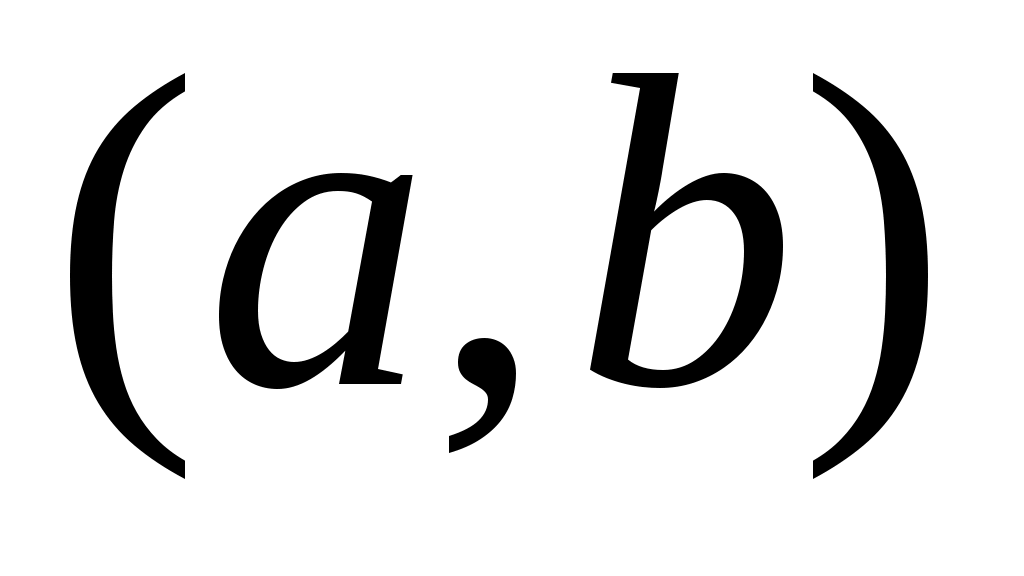 интервалы интервалы 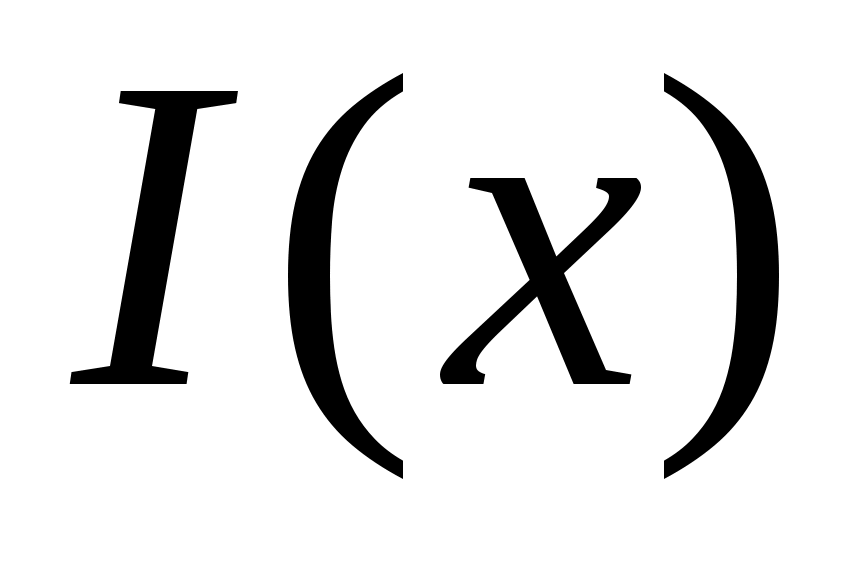 жиынымен беттеседі (Осыны дәлелдеңіз.). Ал жиынымен беттеседі (Осыны дәлелдеңіз.). Ал 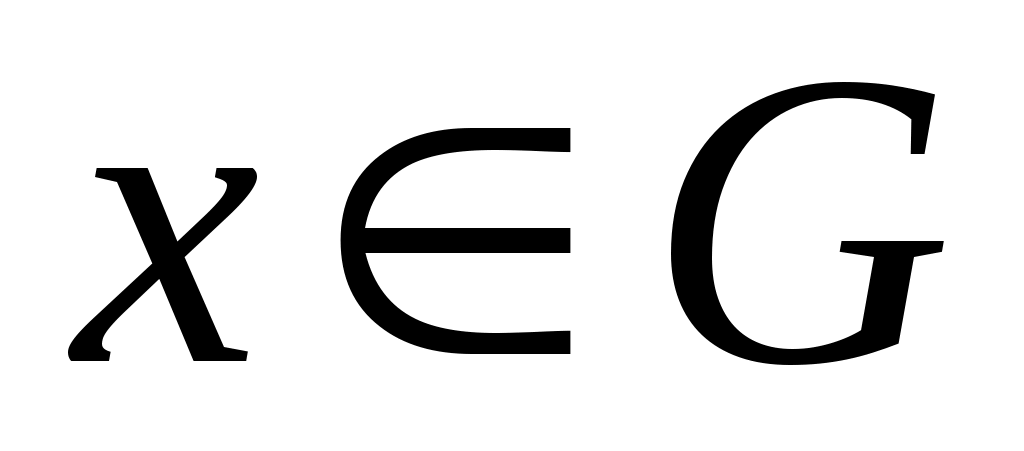 және және 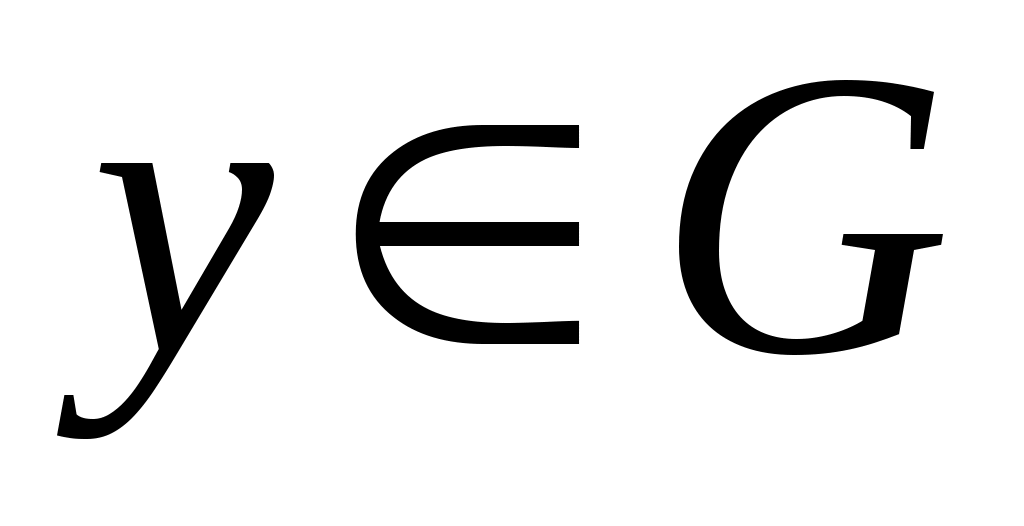 нүктелеріне сәйкес нүктелеріне сәйкес 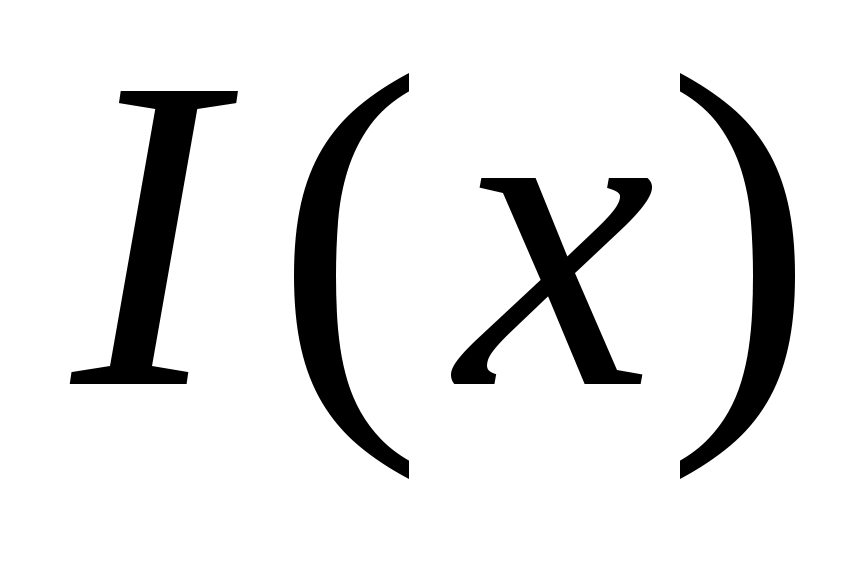 және және 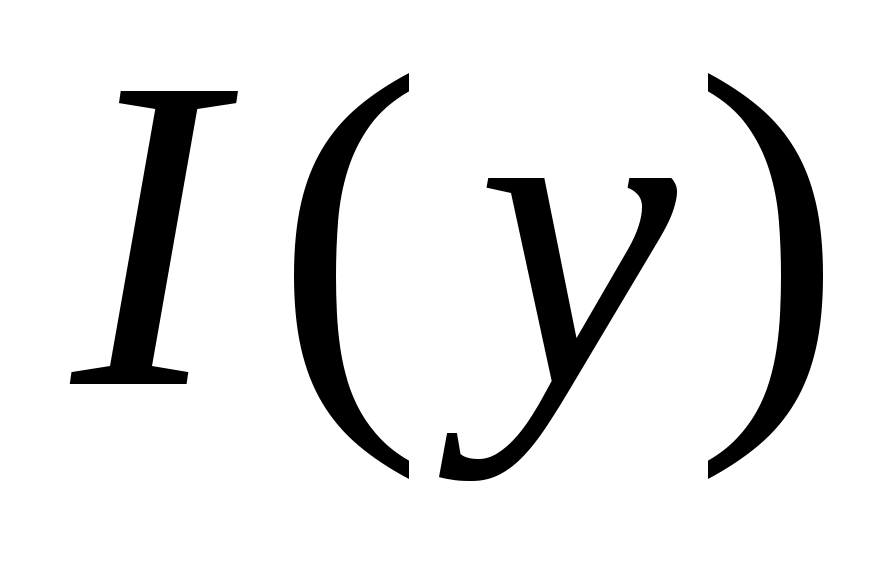 интервалдары беттеседі немесе қиылыспайды. Енді интервалдары беттеседі немесе қиылыспайды. Енді 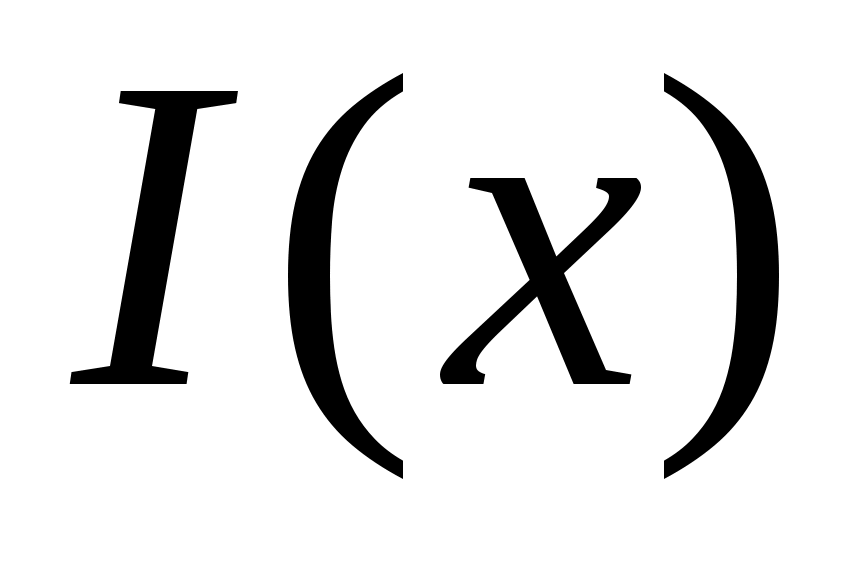 интервалдары арасынан өзара қиылыспайтын интервалдары арасынан өзара қиылыспайтын 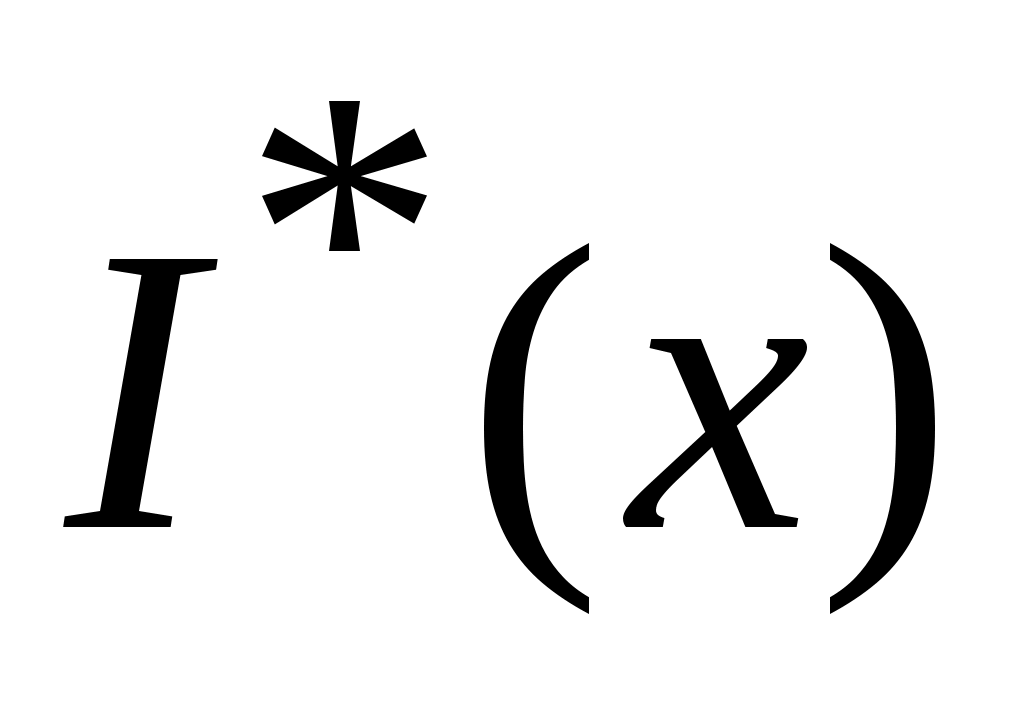 интервалдарын бөліп алсақ, теорема дәлелдеуін аламыз, өйткені, біріншіден, интервалдарын бөліп алсақ, теорема дәлелдеуін аламыз, өйткені, біріншіден, 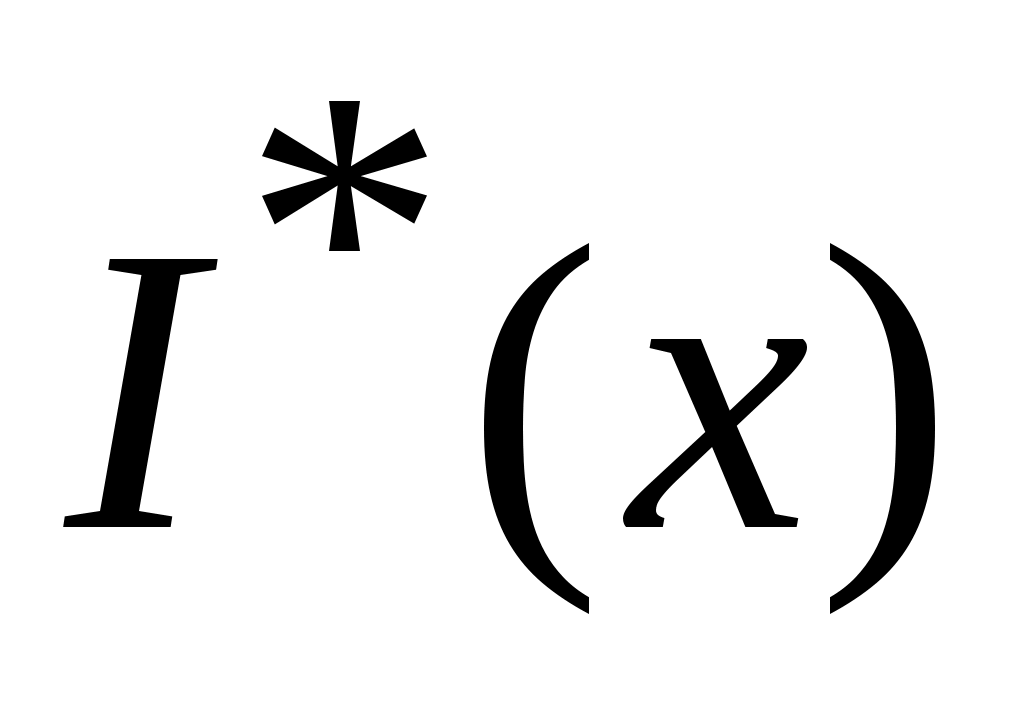 интервалдарының жиыны не ақырлы, не саналымды жиын болады (әрбір интервалдарының жиыны не ақырлы, не саналымды жиын болады (әрбір 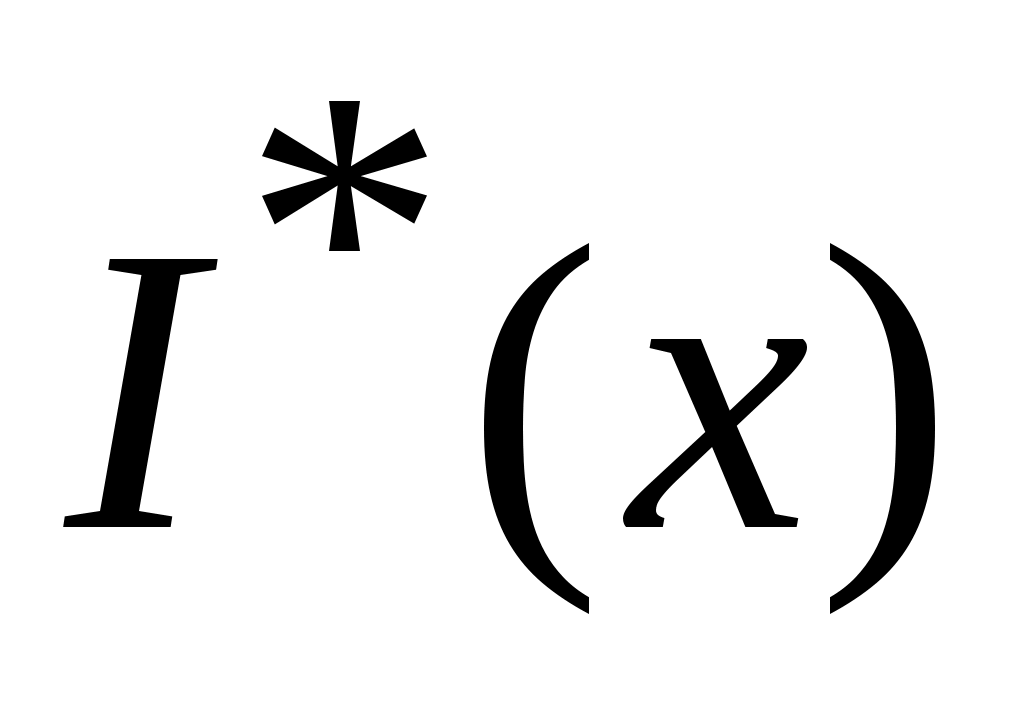 интервалында қайсыбір рационал сан жатады); екіншіден, интервалында қайсыбір рационал сан жатады); екіншіден, 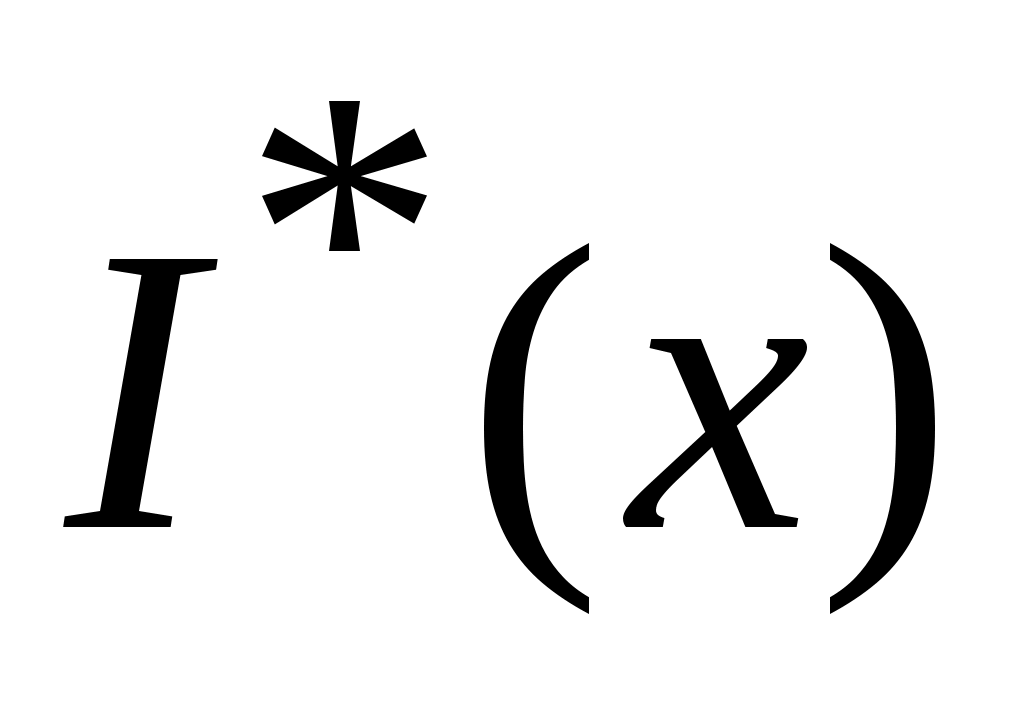 интервалдарының бірігуі интервалдарының бірігуі 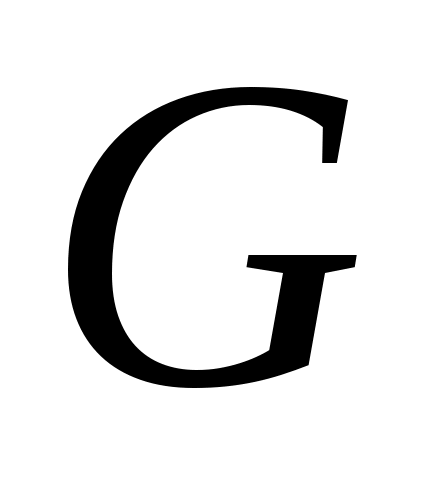 жиынымен беттеседі. жиынымен беттеседі.
Жаттығулар мен есептер
1. Натурал сандар және жұп сандар жиындары арасында өзара бірмәнді сәйкестік орнатыңыз.
2. 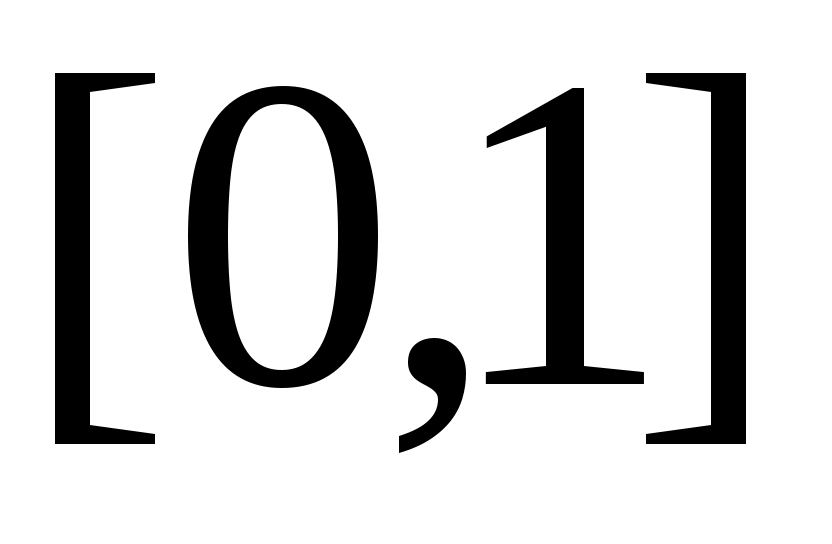 және және 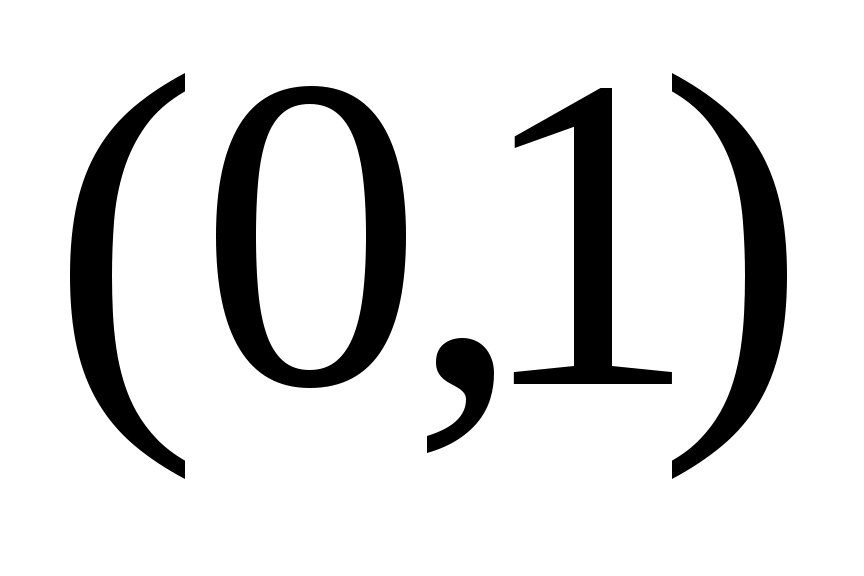 аралықтары арасында өзара бірмәнді сәйкестік құрыңыз. аралықтары арасында өзара бірмәнді сәйкестік құрыңыз.
3. Иррационал сандар және нақты сандар жиындары арасында өзара бірмәнді сәйкестік құрыңыз.
4. Кез келген екі нүктесінің арақашықтығы 1 – ден артық жиынның ақырлы немесе саналымды жиын екеніне көз жеткізіңіз.
5. Егер  саналымды емес, ал саналымды емес, ал 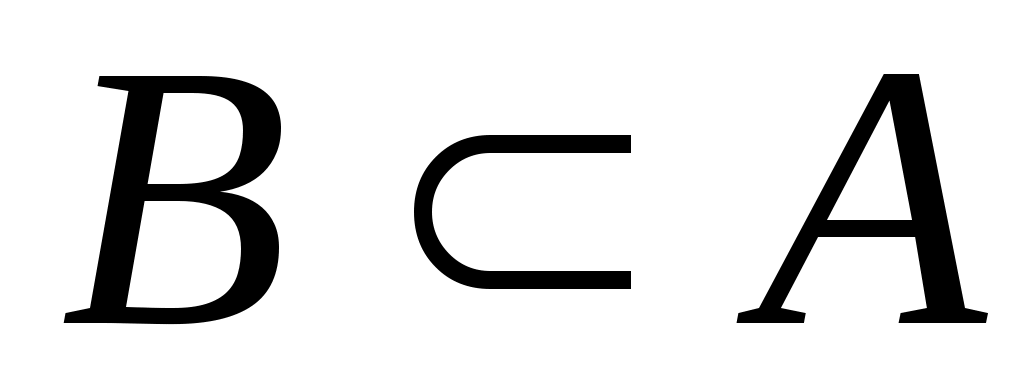 жиыны саналымды болса, онда жиыны саналымды болса, онда 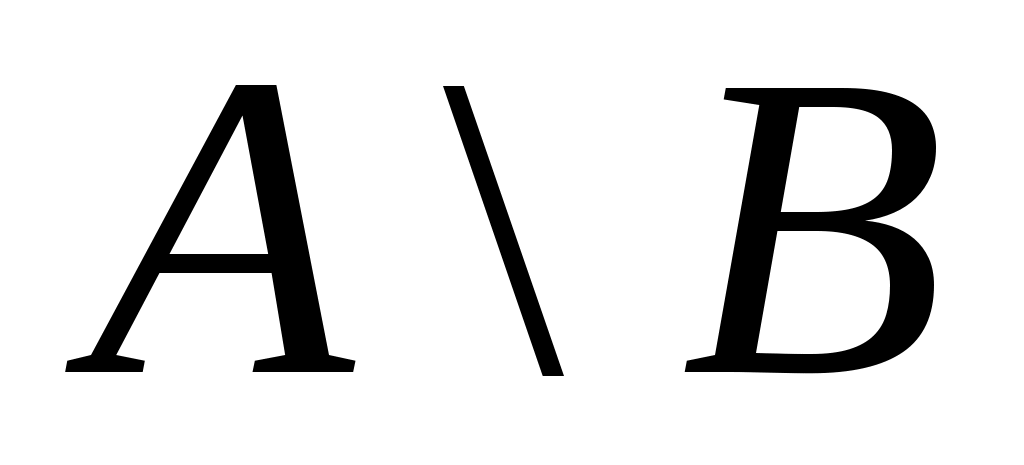 жиыны саналымды жиын бола ма? жиыны саналымды жиын бола ма?
6. Саналымды 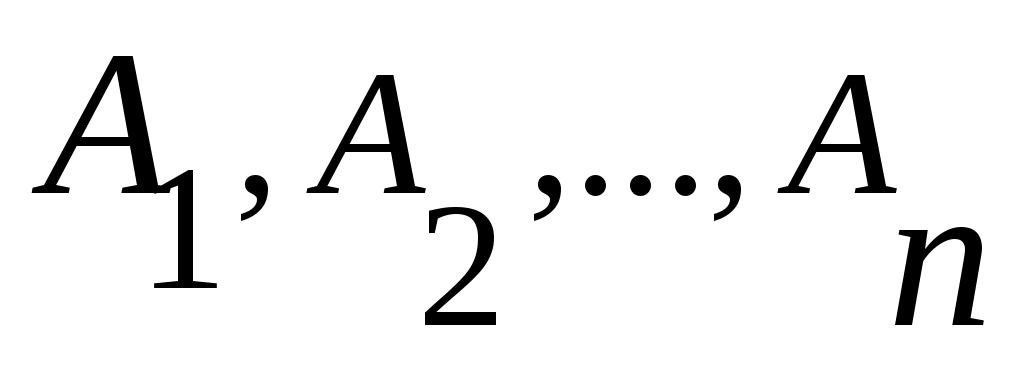 жиындары үшін жиындары үшін 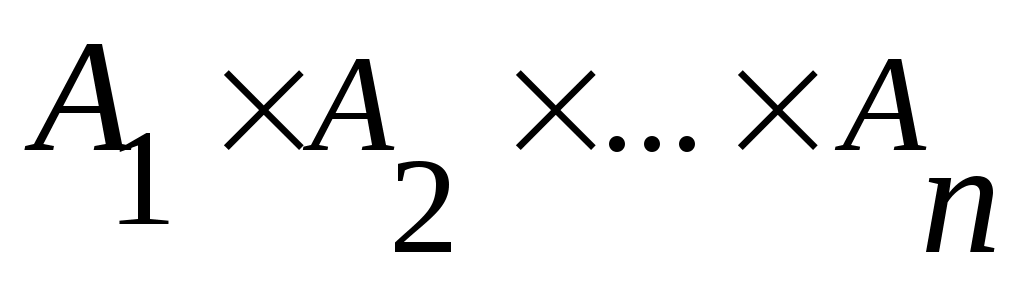 жиыны саналымды жиын екеніне көз жеткізіңіз. жиыны саналымды жиын екеніне көз жеткізіңіз.
7. Дәлелдеңіз: а) Алгебралық сандар жиыны – саналымды жиын;
ә) Коэффициенттері рационал көпмүшеліктер жиыны – саналымды жиын;
б) 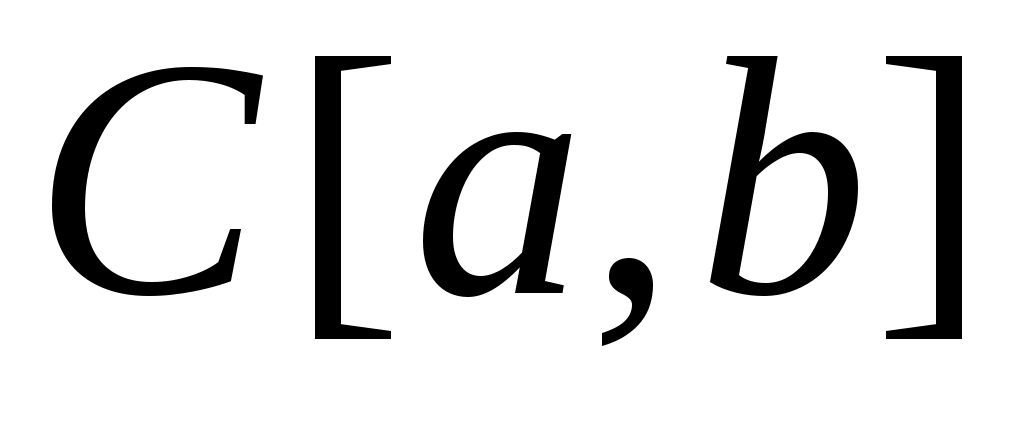 жиыны – континуалды жиын; в) Кантор жиыны – континуалды жиын. жиыны – континуалды жиын; в) Кантор жиыны – континуалды жиын.
8. Дәлелдеңіз: Әрбір  саны үшін саны үшін 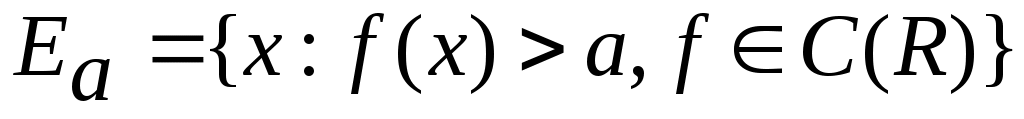 жиыны – ашық жиын. жиыны – ашық жиын.
9. 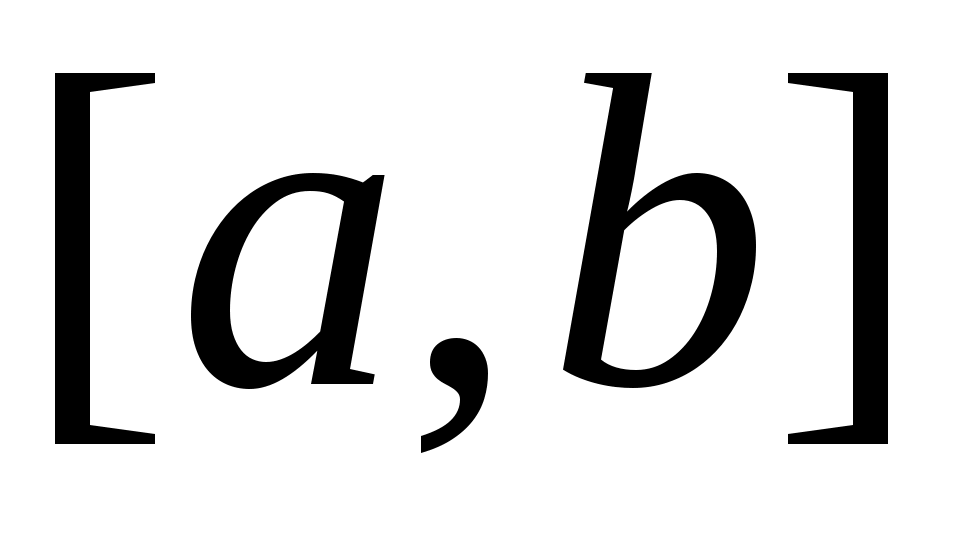 сегменті бос емес, қиылыспайтын екі тұйық жиынның бірігуі болуы мүмкін бе? сегменті бос емес, қиылыспайтын екі тұйық жиынның бірігуі болуы мүмкін бе?
10. Дәлелдеңіз: Егер 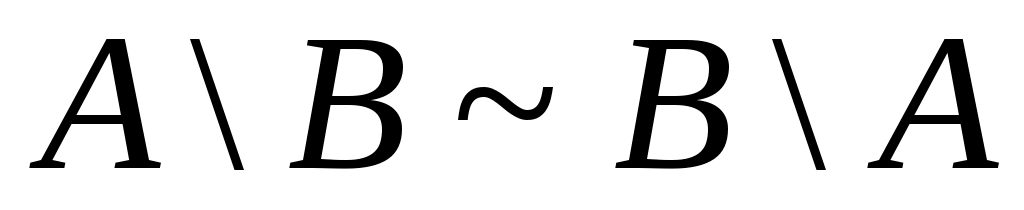 болса, онда болса, онда 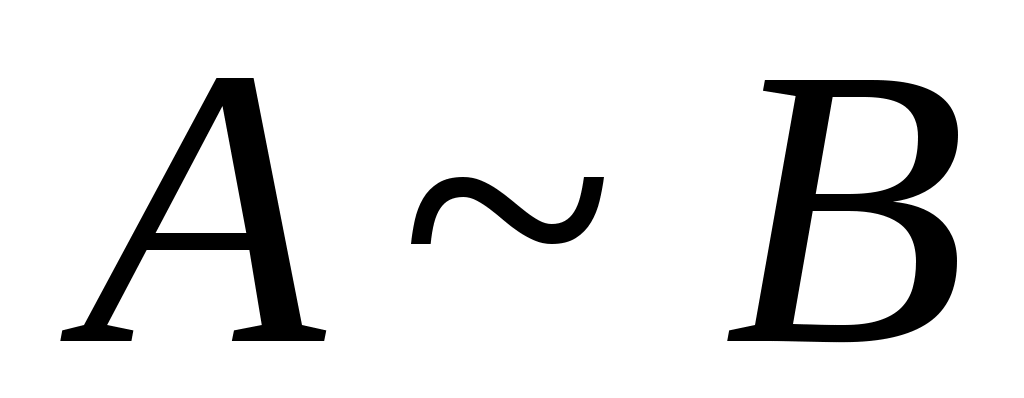 . .
11. Әрбір мүшесі нақты сандар жиынында жататын тізбектер жиынының қуаты континуум екенін дәлелдеңіз.
12. Комплекс сандар жиынының қуаты қандай?
13. Жай сандар жиынының саналымды жиын екеніне көз жеткізіңіз.
14. 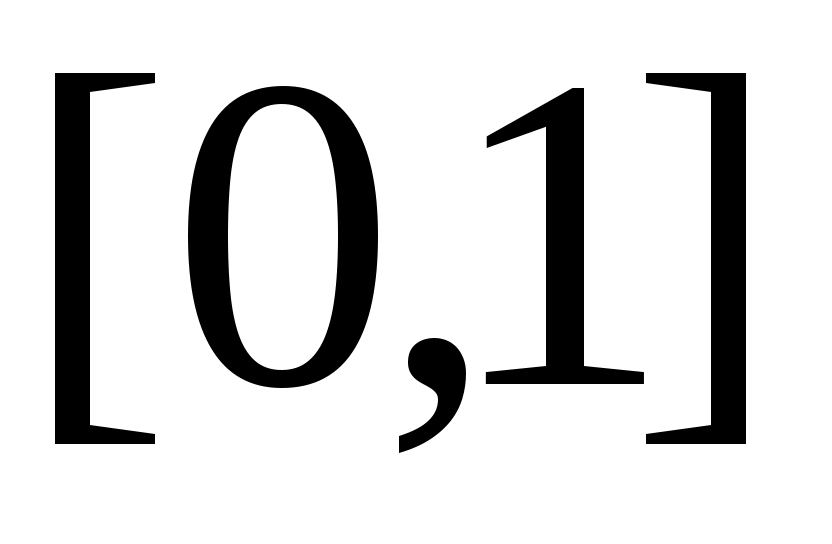 және және 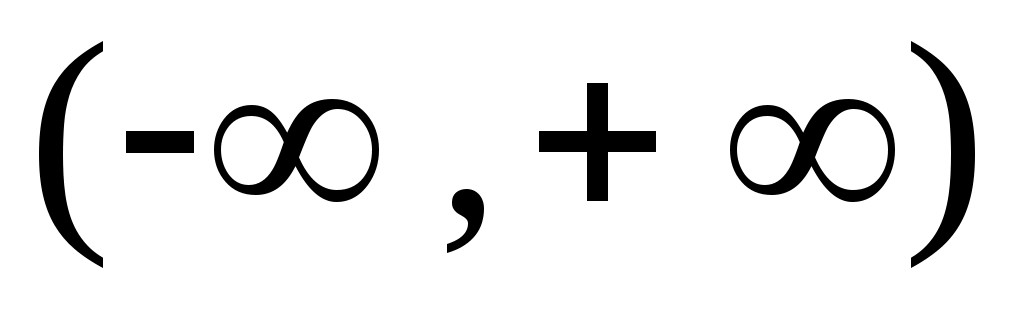 аралықтары арасында өзара бірмәнді сәйкестік орнататын үзіліссіз функция бар ма? аралықтары арасында өзара бірмәнді сәйкестік орнататын үзіліссіз функция бар ма?
15. Дәлелдеңіз: Әрбір  үшін үшін 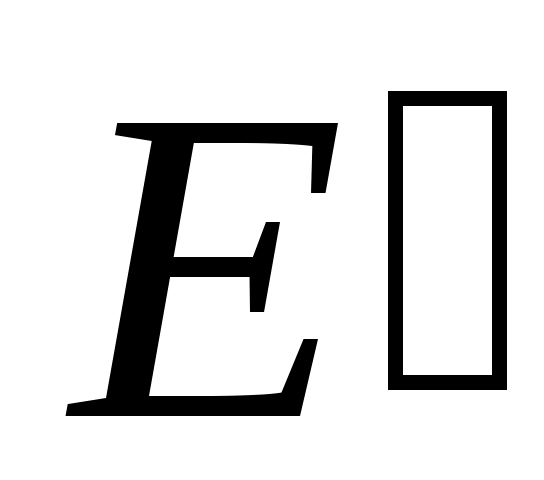 жиыны – тұйық жиын. жиыны – тұйық жиын.
|
|
|
 Скачать 1.5 Mb.
Скачать 1.5 Mb.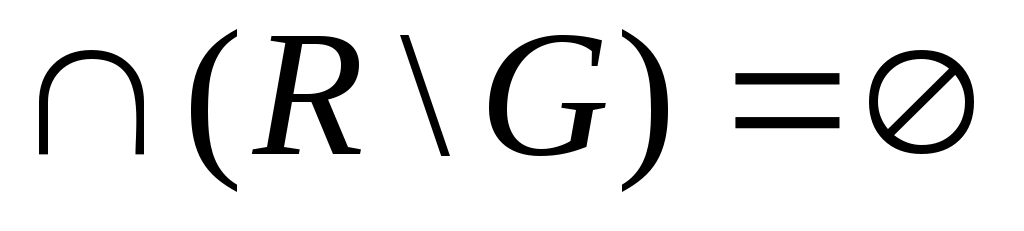 теңдігі орындалады. Бұл теңдік
теңдігі орындалады. Бұл теңдік 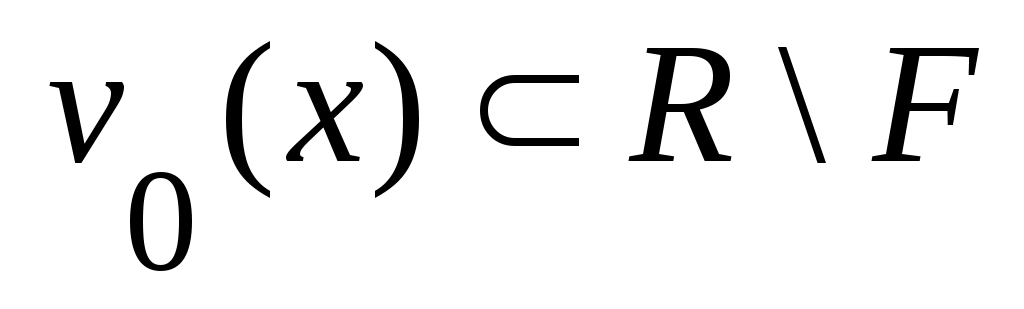 . Сонымен,
. Сонымен, 