|
|
ГЛ1. 1 тарау. Жиындар теориясыны элементтері жиыны жиыныны жиыншасы болан жадайда жиыны жиынын амтиды
§3. Саналымды жиындар
1 – анықтама. Ақырсыз 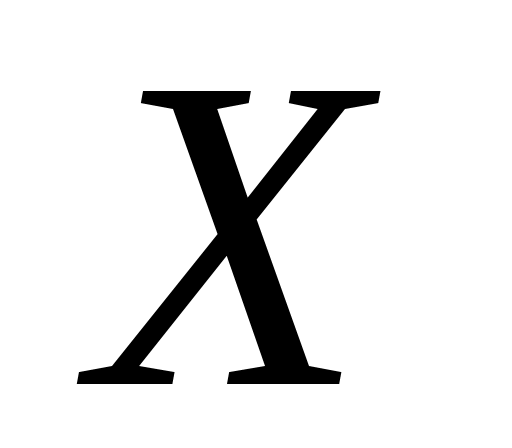 жиыны берілсін. Егер жиыны берілсін. Егер 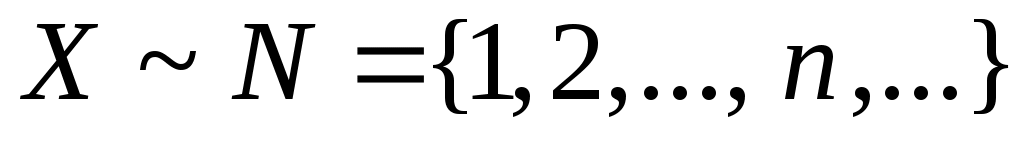
эквиваленттілігі орындалатын болса, онда 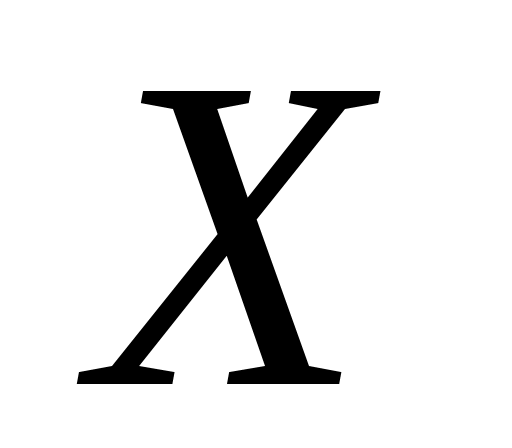 жиынын «саналымды жиын» немесе «қуаты жиынын «саналымды жиын» немесе «қуаты  жиын» деп атаймыз. жиын» деп атаймыз.
Төменде 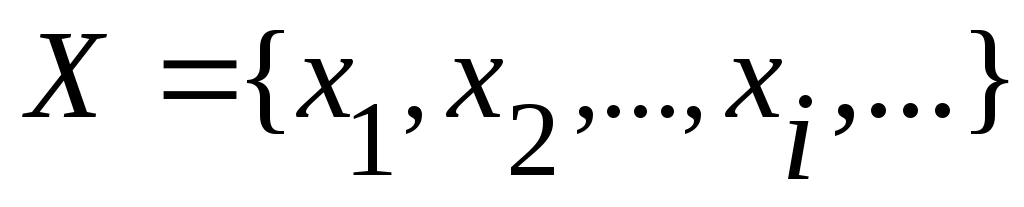 жазуы жазуы 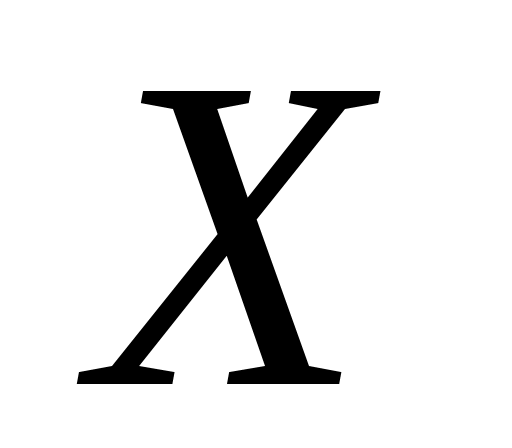 жиынының саналымды жиын екенін білдіретін болады. жиынының саналымды жиын екенін білдіретін болады. 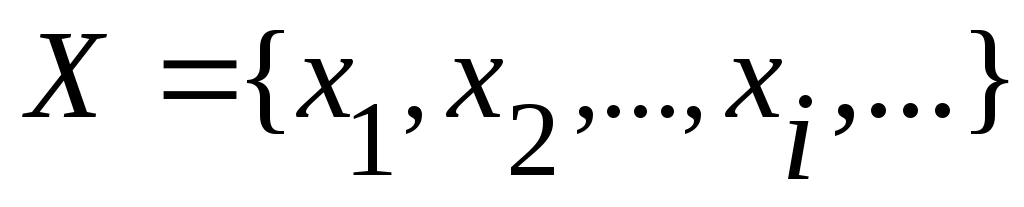 жазуында жазуында 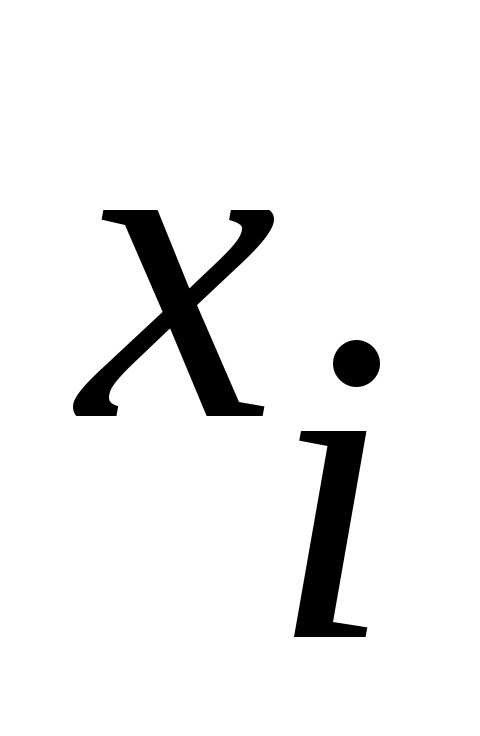 арқылы арқылы 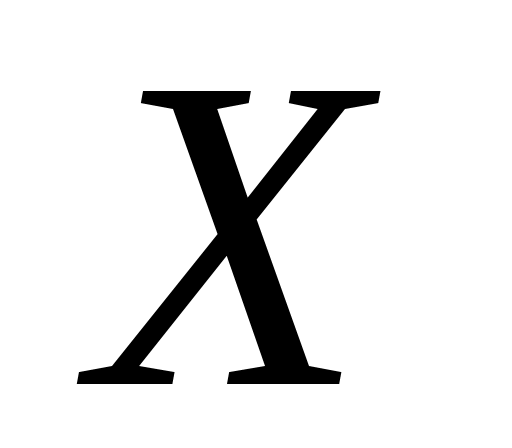 жиынының жиынының 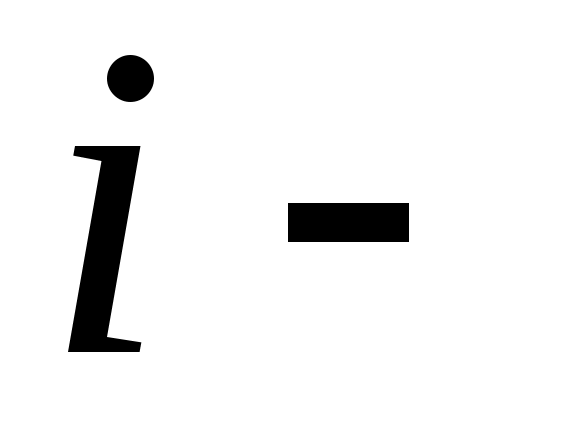 ші нөмірге сәйкес элементі белгіленген. ші нөмірге сәйкес элементі белгіленген.
Мысал келтірейік. Бүтін сандар жиыны ( жиыны) – саналымды жиын: жиыны) – саналымды жиын:
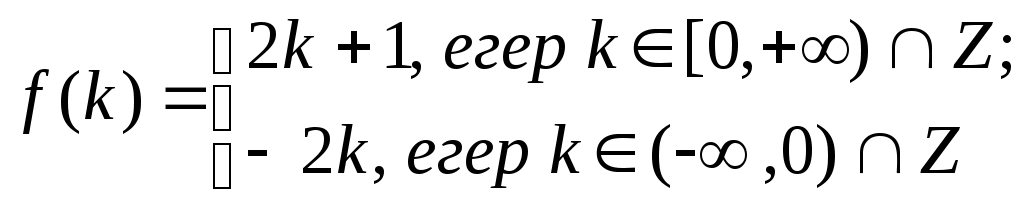 теңдігін қанағаттандыратын теңдігін қанағаттандыратын 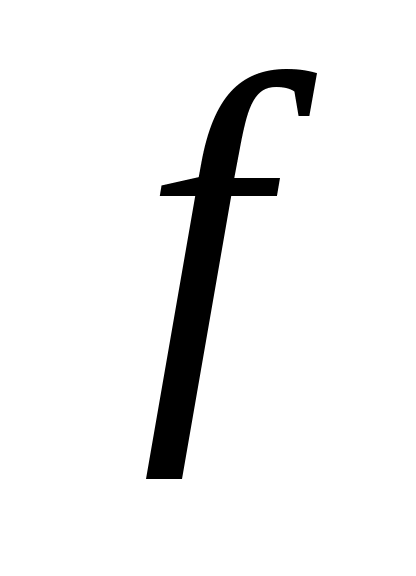 функциясы функциясы  және және 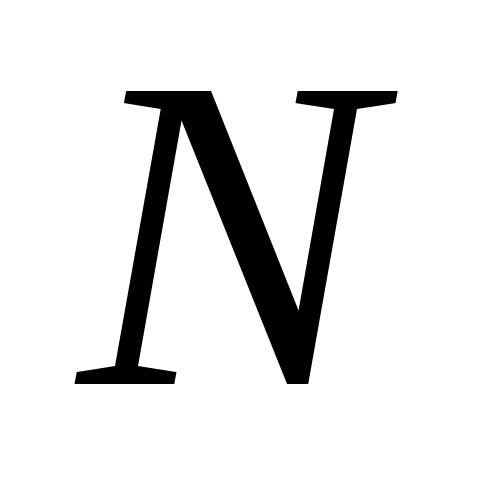 жиындары арасында өзара бірмәнді сәйкестік орнатады. жиындары арасында өзара бірмәнді сәйкестік орнатады.
Келесі теоремада ақырсыз, бірақ саналымды емесжиын бар екені көрсетіледі.
1– теорема. 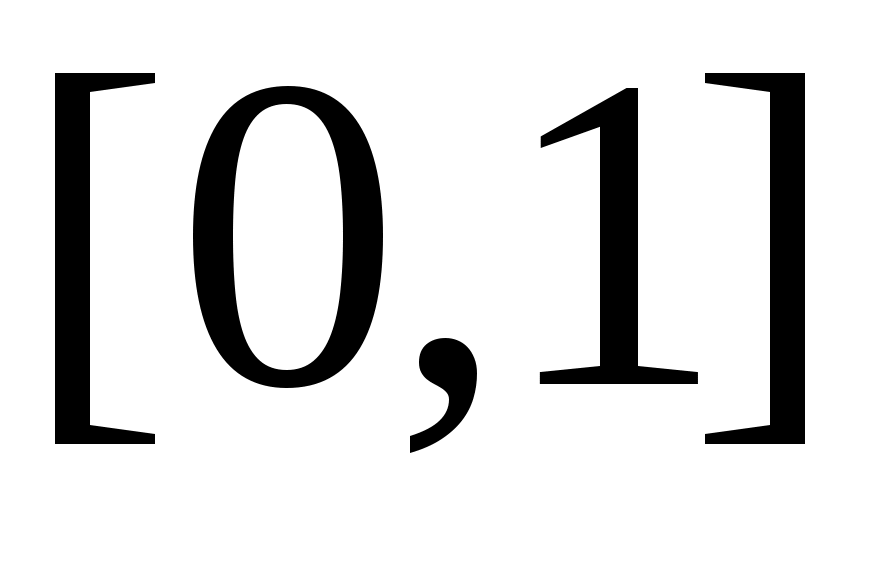 сегменті саналымды жиын емес. сегменті саналымды жиын емес.
Дәлелдеуі. Кері жорып, 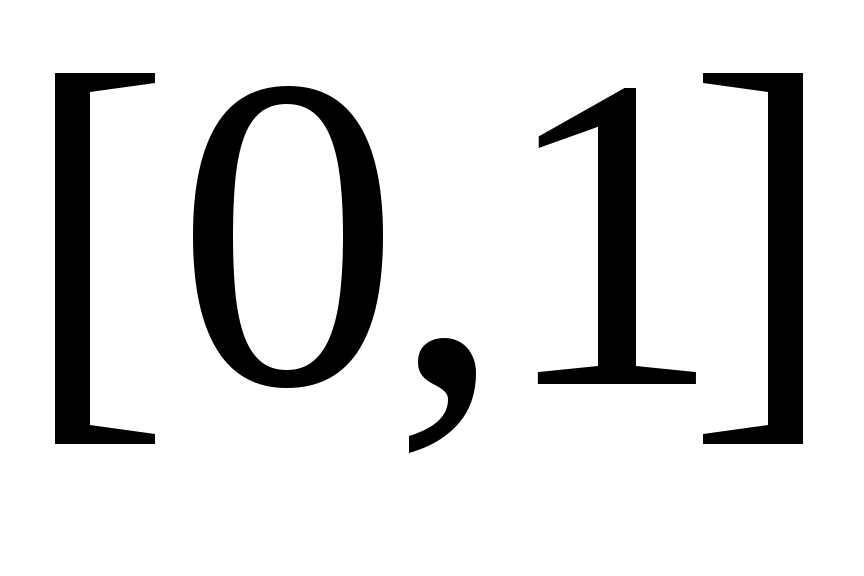 сегменті саналымды жиын болсын дейік және сегменті саналымды жиын болсын дейік және
осы сегменттің 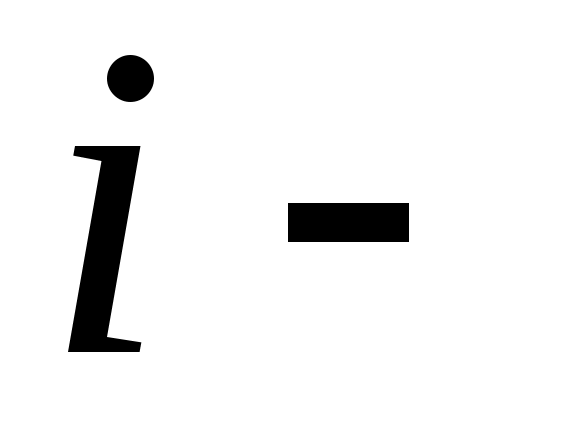 ші нөмірге сәйкес элементін ші нөмірге сәйкес элементін 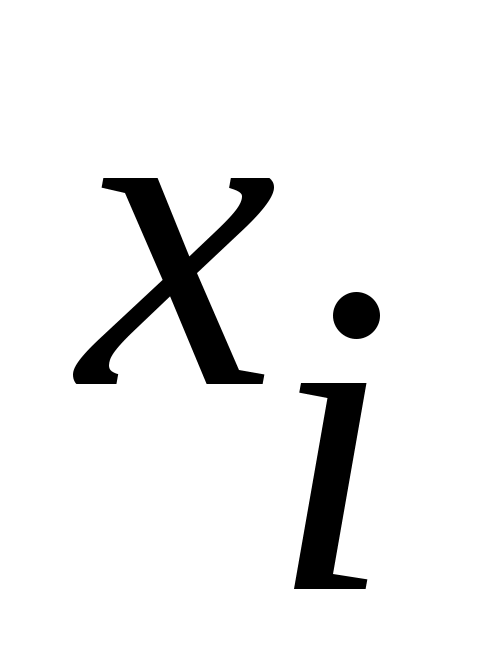 арқылы таңбалайық. арқылы таңбалайық.
Енді 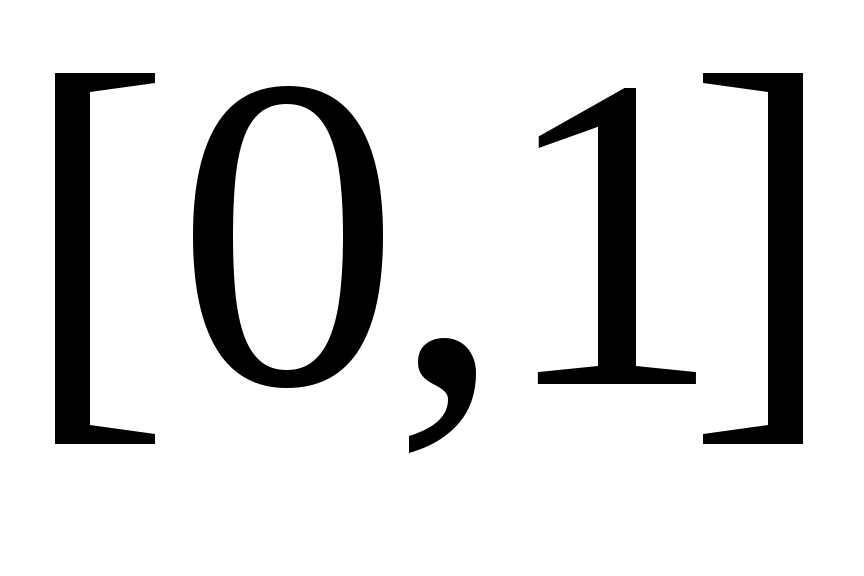 сегментін ұзындықтары бірдей үш сегментке бөлеміз: сегментін ұзындықтары бірдей үш сегментке бөлеміз: 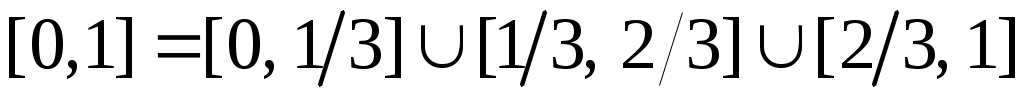 . . 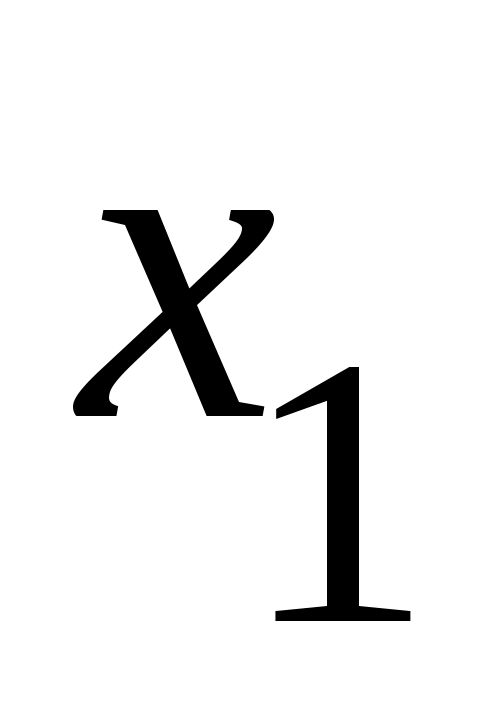 элементі осы сегменттердің кемінде бірінде жатпайды. Сол сегментті элементі осы сегменттердің кемінде бірінде жатпайды. Сол сегментті 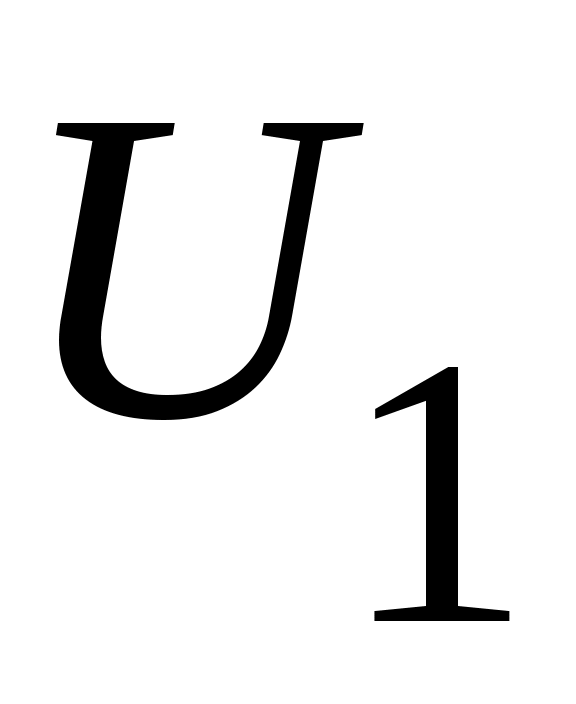 арқылы белгілейік те, арқылы белгілейік те, 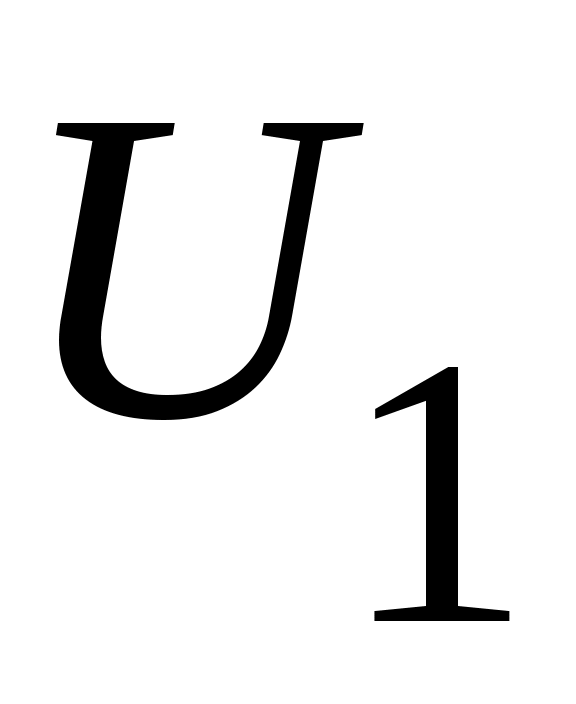 сегментін де ұзындықтары бірдей үш сегментке бөлейік және сегментін де ұзындықтары бірдей үш сегментке бөлейік және 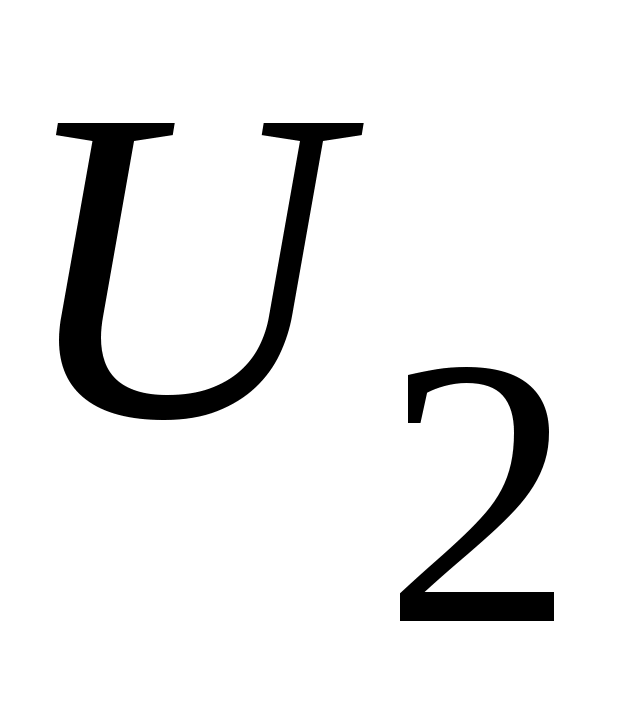 арқылы арқылы 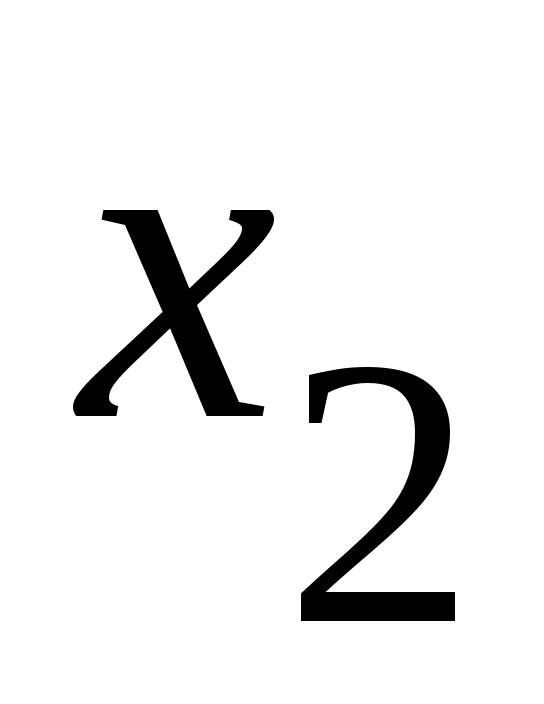 элементі жатпайтын сегменттің бірін белгілейік. Осылай жалғастыра берсек, элементі жатпайтын сегменттің бірін белгілейік. Осылай жалғастыра берсек, 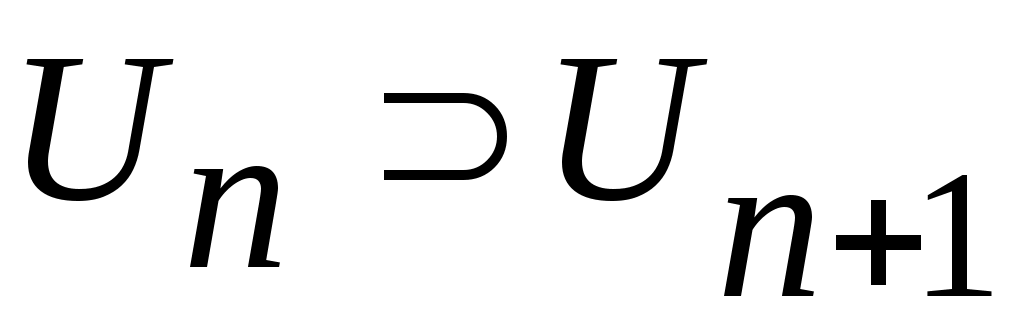 , , 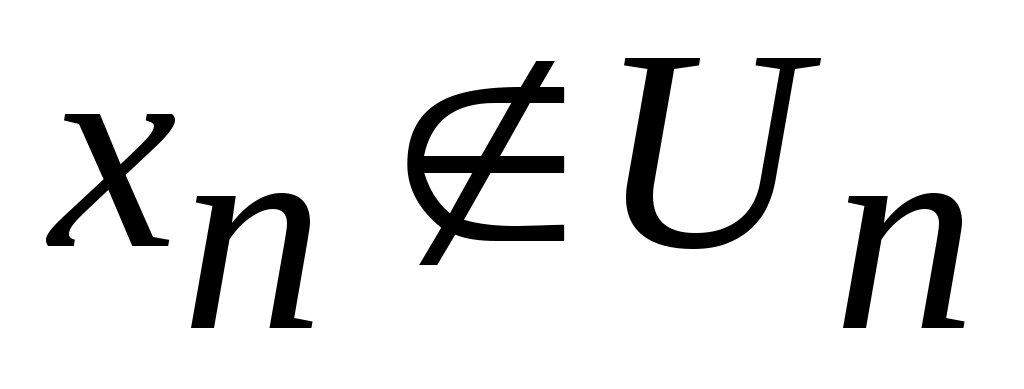 шарттарын қанағаттандыратын шарттарын қанағаттандыратын 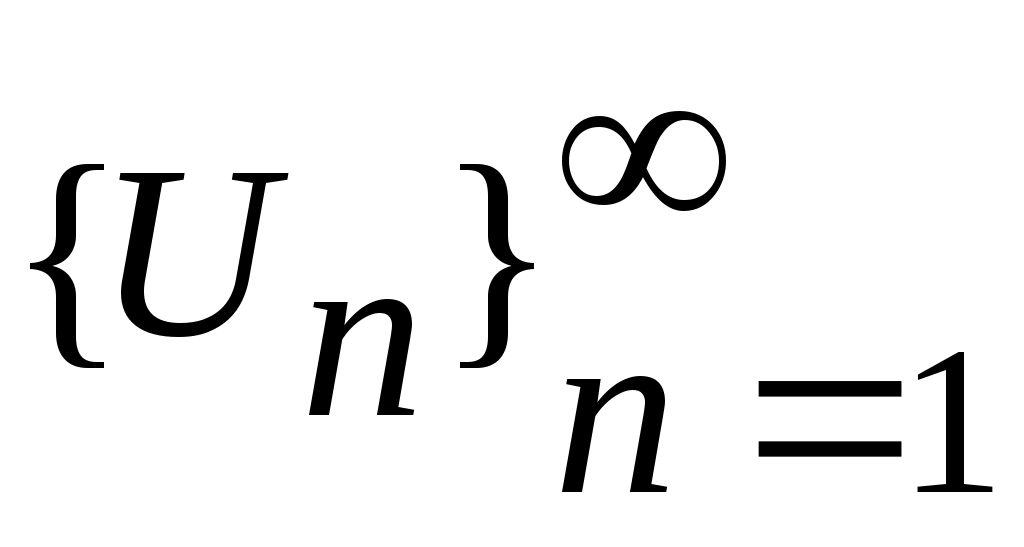 тізбегін аламыз. Сегменттер ұясы туралы теорема (қараңыз, [5], 76 – бет) бойынша тізбегін аламыз. Сегменттер ұясы туралы теорема (қараңыз, [5], 76 – бет) бойынша 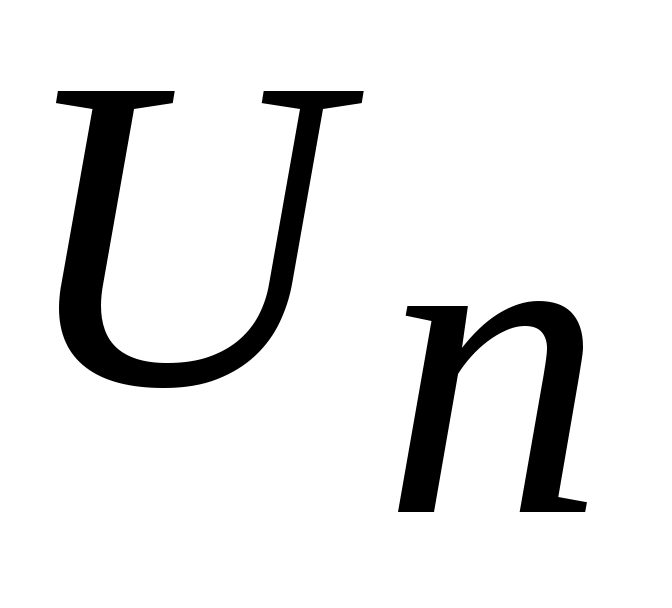 сегментінің сегментінің
әрқайсысында жататын жалғыз 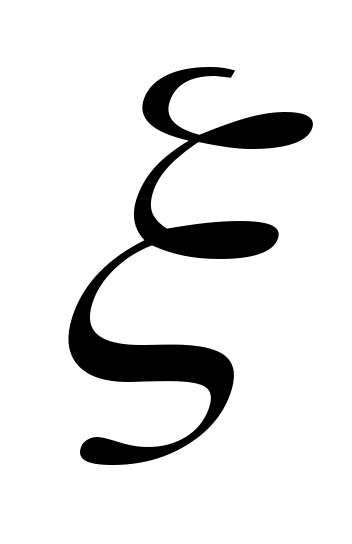 нүктесі бар болады. Ал нүктесі бар болады. Ал 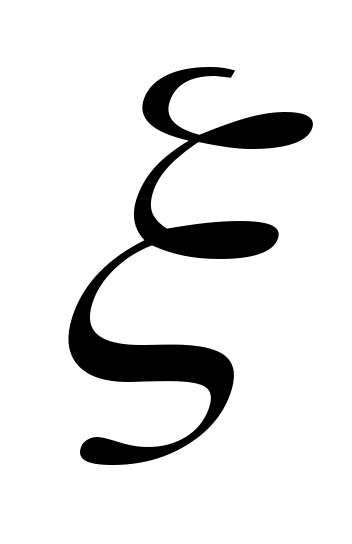 нүктесі нүктесі 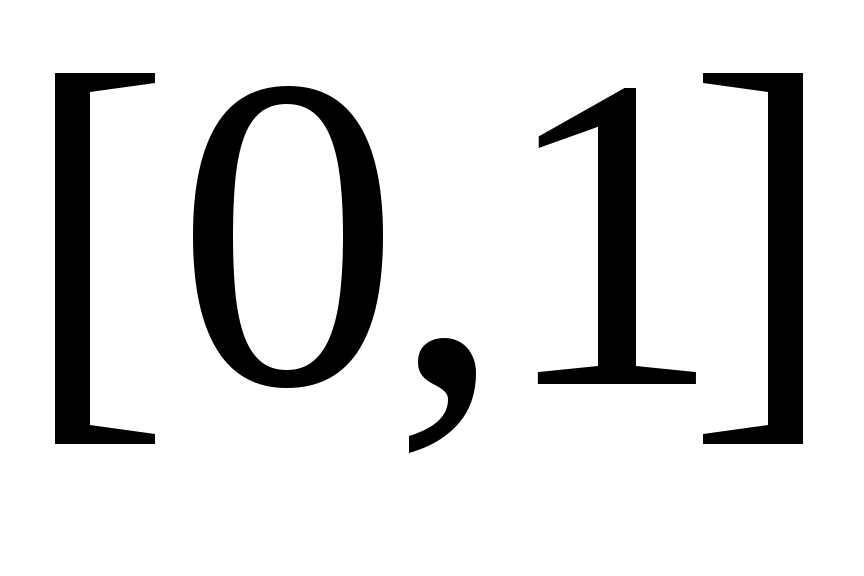 сегментінде жататындықтан, жоруымыз бойынша, қайсыбір сегментінде жататындықтан, жоруымыз бойынша, қайсыбір 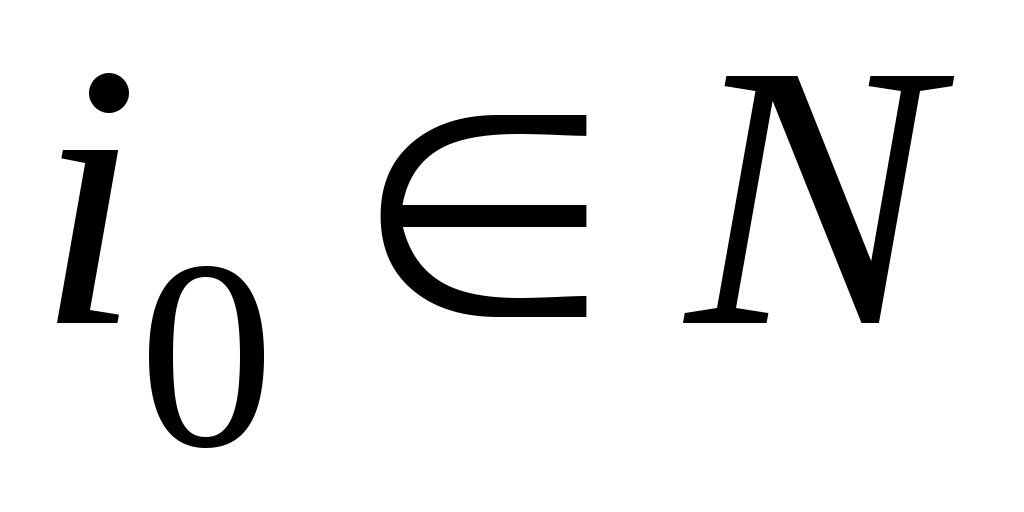 үшін үшін 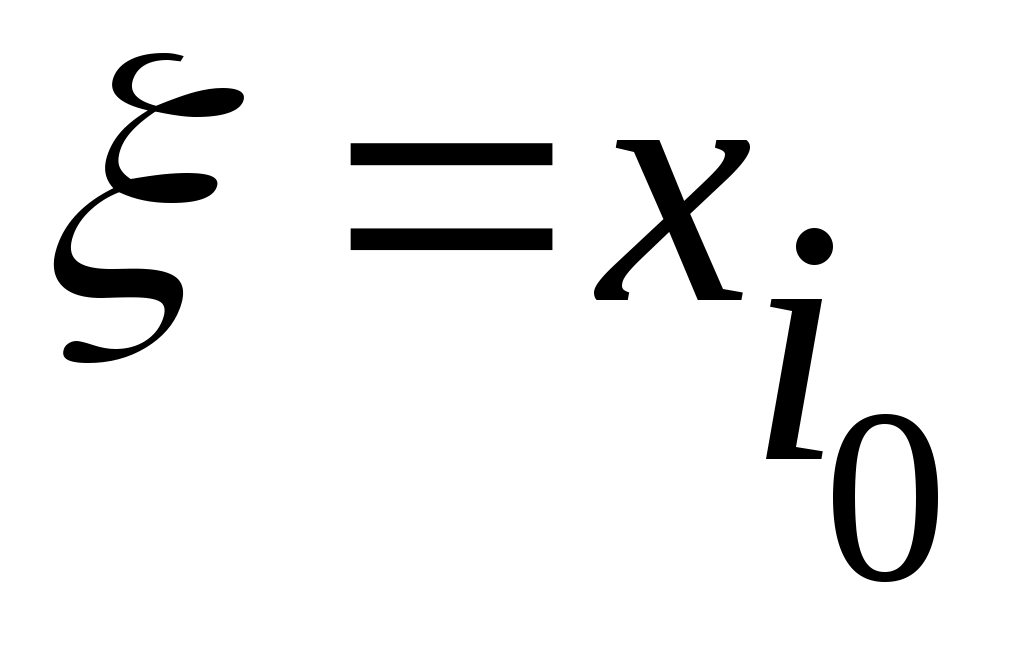 теңдігі орындалады. Бұдан қайшылыққа келеміз: теңдігі орындалады. Бұдан қайшылыққа келеміз: 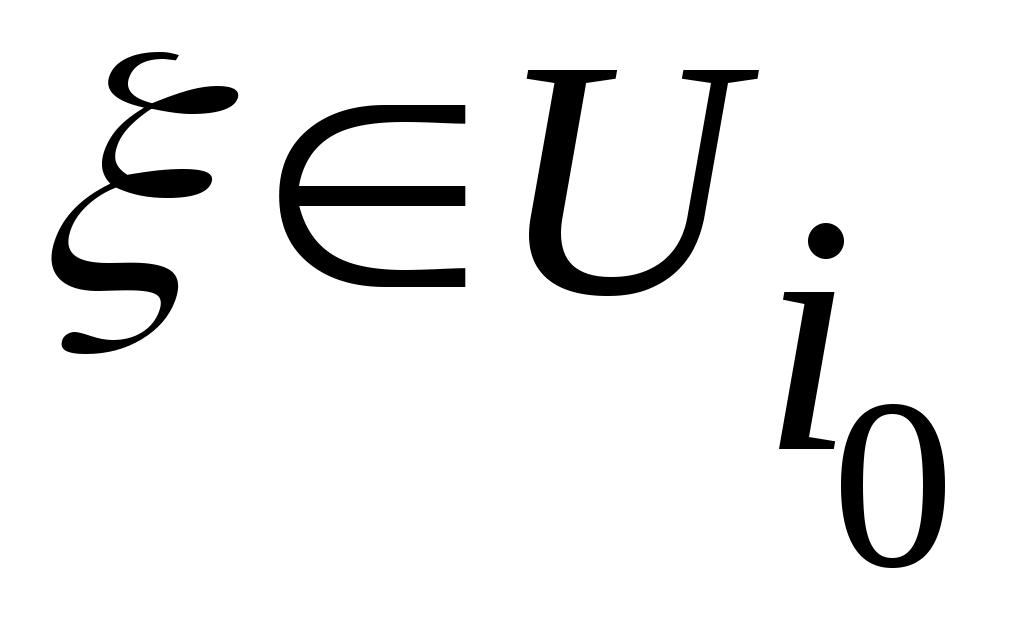 және және 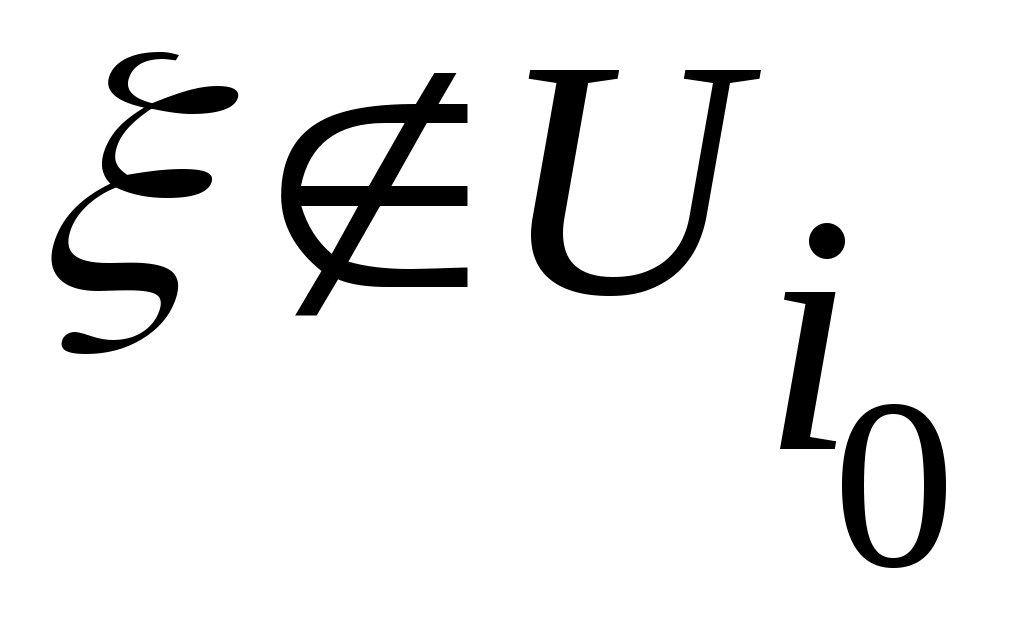 . Ендеше, . Ендеше, 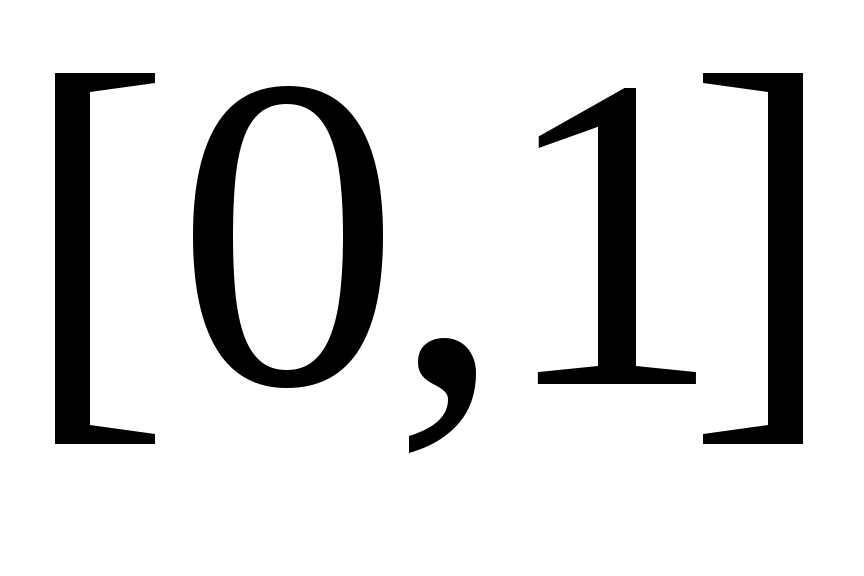 сегменті саналымды жиын емес. сегменті саналымды жиын емес.
Енді саналымды жиындардың қасиеттерін келтірейік.
2 – теорема. Егер ақырлы  және саналымды және саналымды 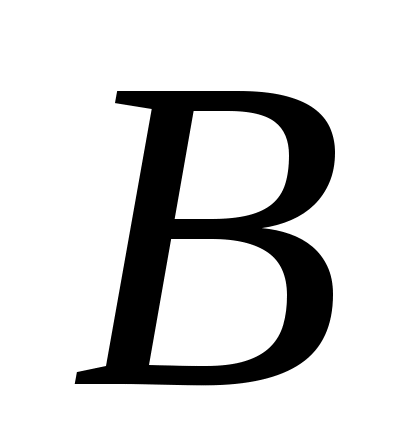 жиындары қиылыс – пайтын болса, онда жиындары қиылыс – пайтын болса, онда  жиыны саналымды жиын болады. жиыны саналымды жиын болады.
Дәлелдеуі. 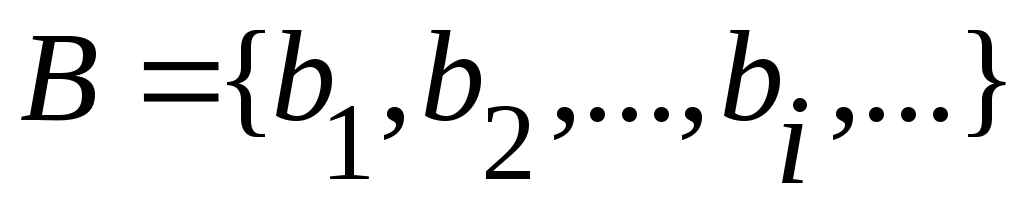 болсын. Егер болсын. Егер 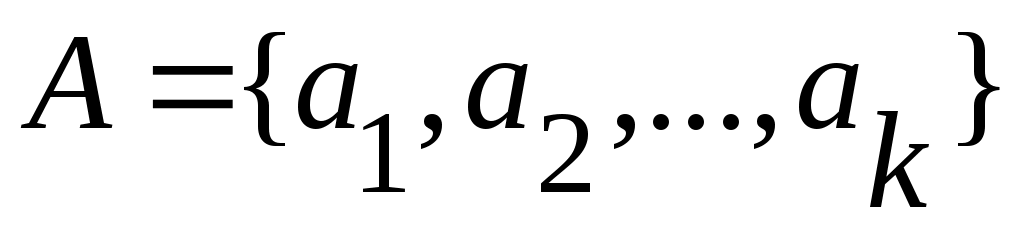 болса, онда болса, онда
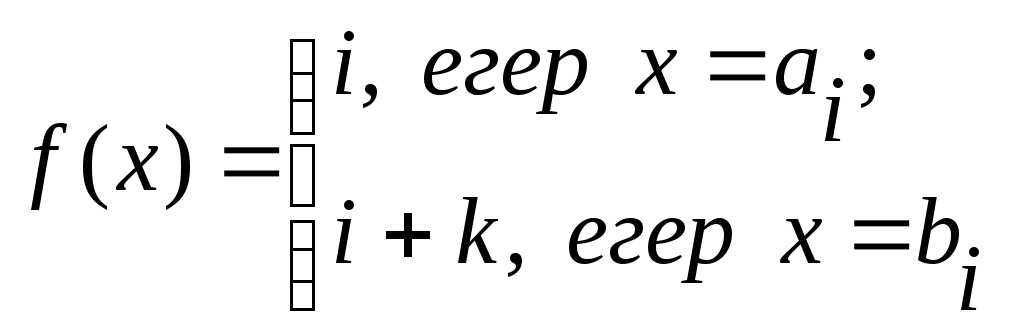 теңдігін қанағаттандыратын теңдігін қанағаттандыратын 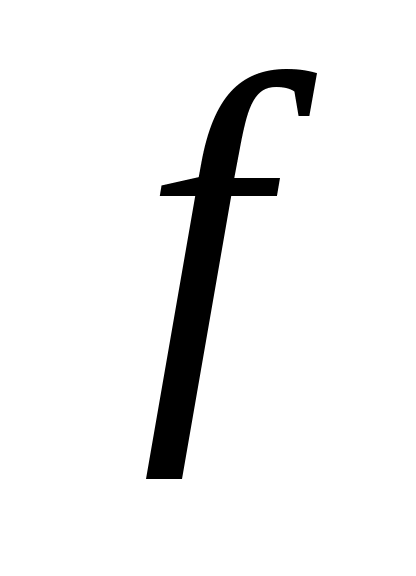 функциясы функциясы  және және 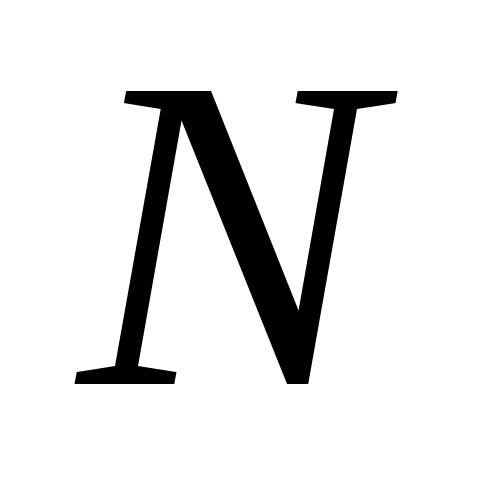 жиындары арасында өзара бірмәнді сәйкестік орнатады. жиындары арасында өзара бірмәнді сәйкестік орнатады.
3 – теорема. Егер ақырлы 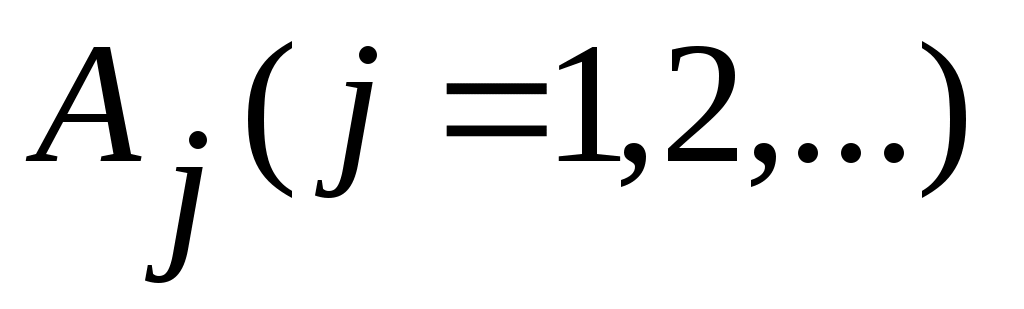 жиындары өзара қиылыспайтын жиындары өзара қиылыспайтын
болса, онда 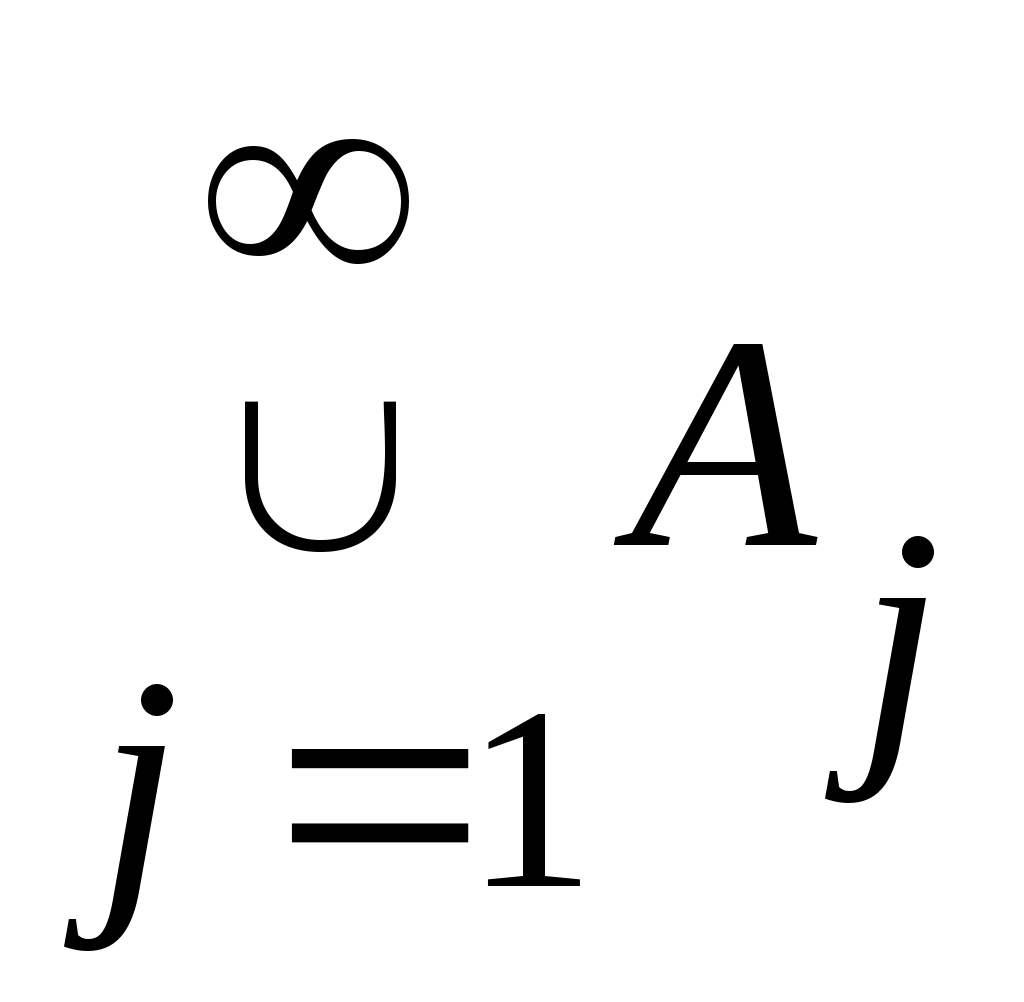 жиыны саналымды жиын болады. жиыны саналымды жиын болады.
Дәлелдеуі. Егер әрбір 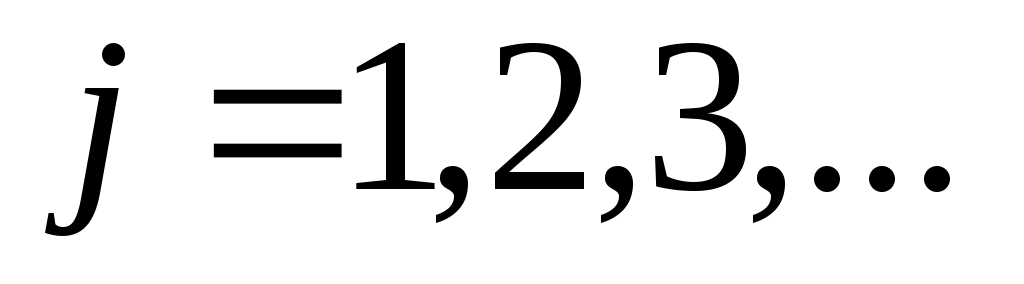 үшін үшін 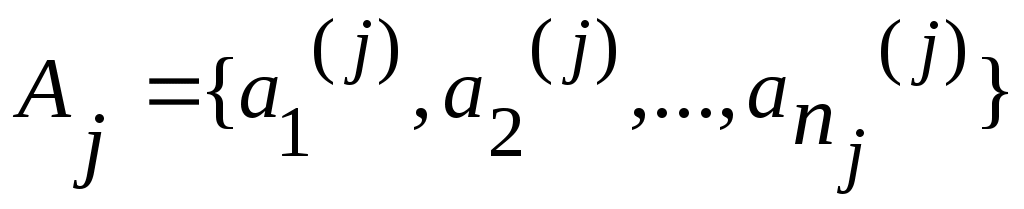 болса, болса,
онда 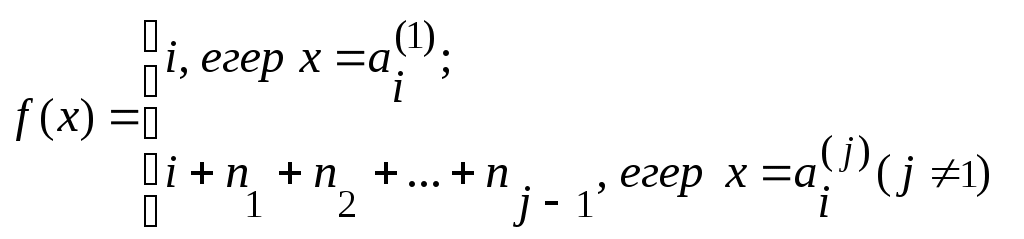 теңдігі бойынша теңдігі бойынша
анықталған 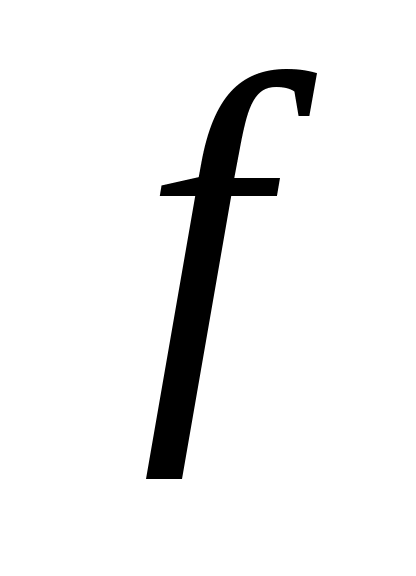 функциясы функциясы 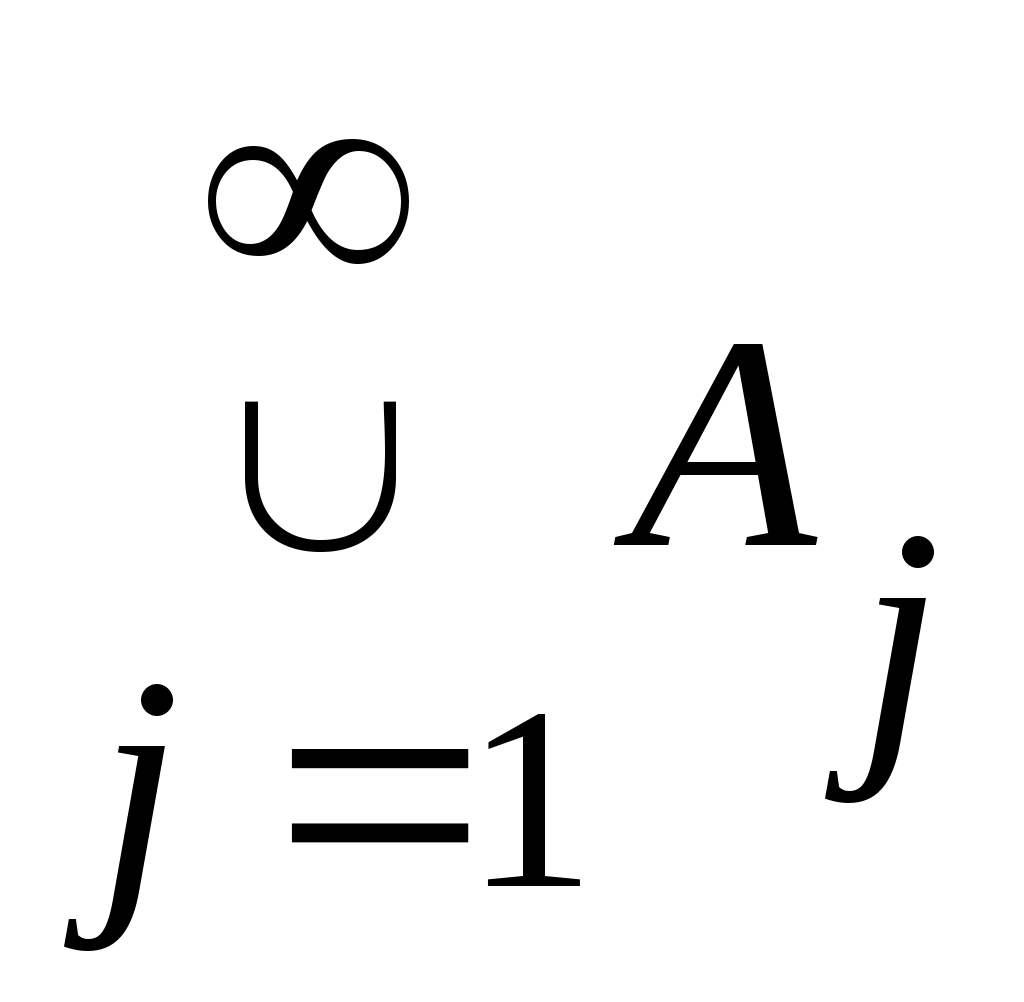 және және 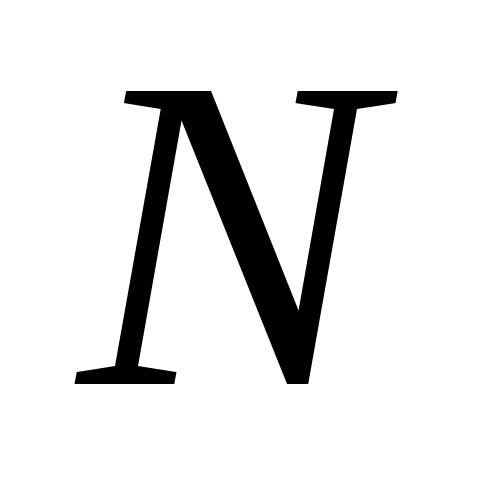 жиындары арасында өзара бірмәнді сәйкестік орнатады. жиындары арасында өзара бірмәнді сәйкестік орнатады.
3 – теорема былай да айтылады:Өзара қиылыспайтын ақырлы жиындар – дың саналымды бірігуі – саналымды жиын.
4 – теорема. Егер саналымды  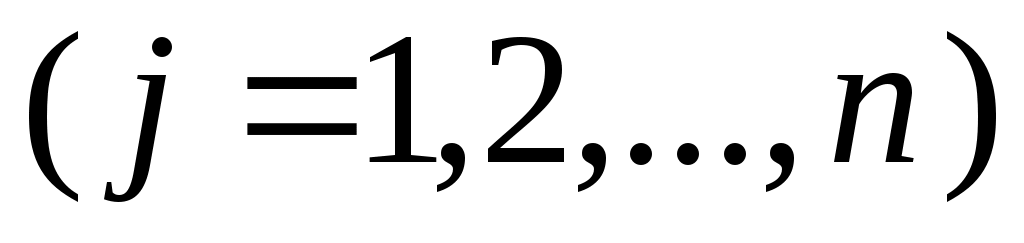 жиындары өзара қиылыс – пайтын болса, онда жиындары өзара қиылыс – пайтын болса, онда 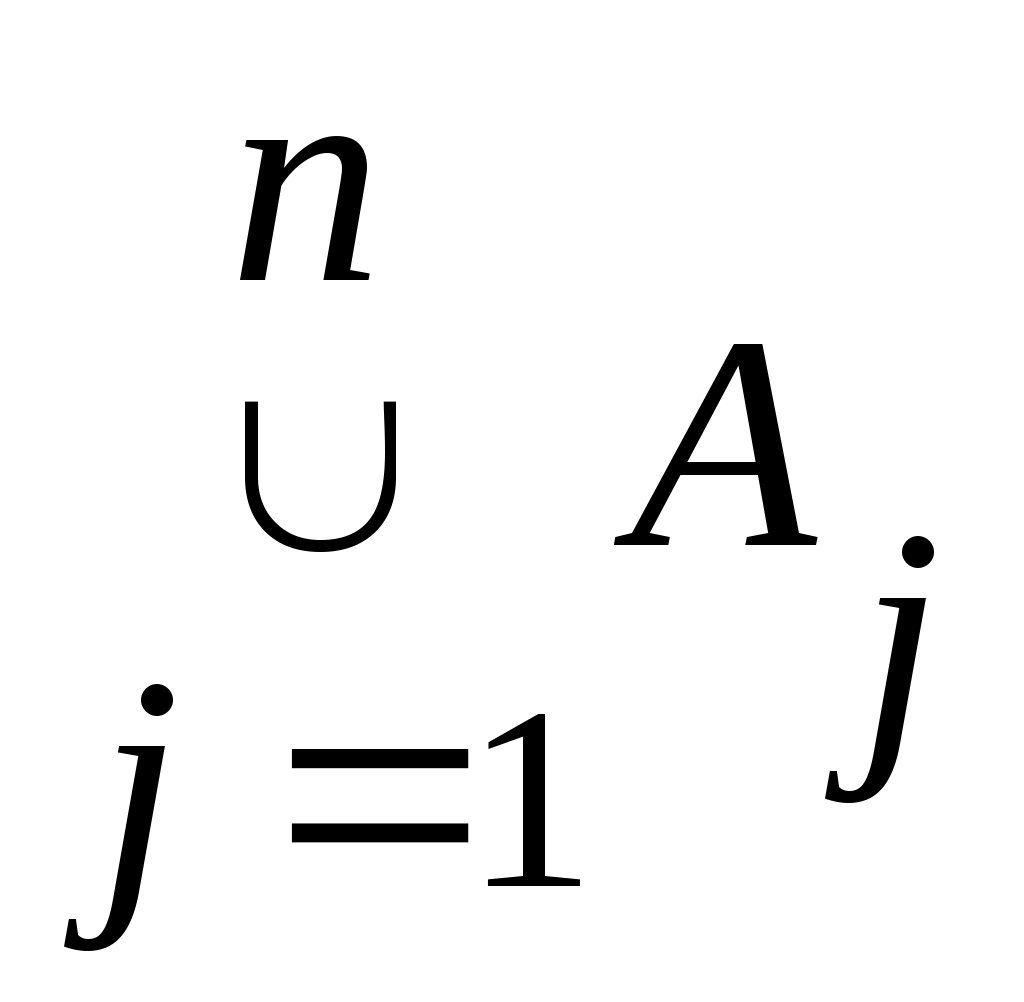 жиыны саналымды жиын болады. жиыны саналымды жиын болады.
Дәлелдеуі.  жиынының жиынының 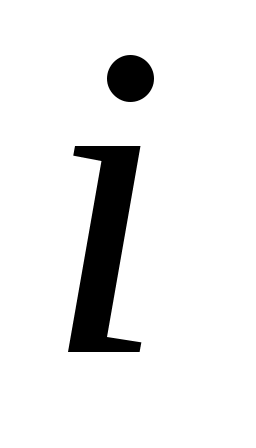 –ші нөмірге сәйкес элементін –ші нөмірге сәйкес элементін 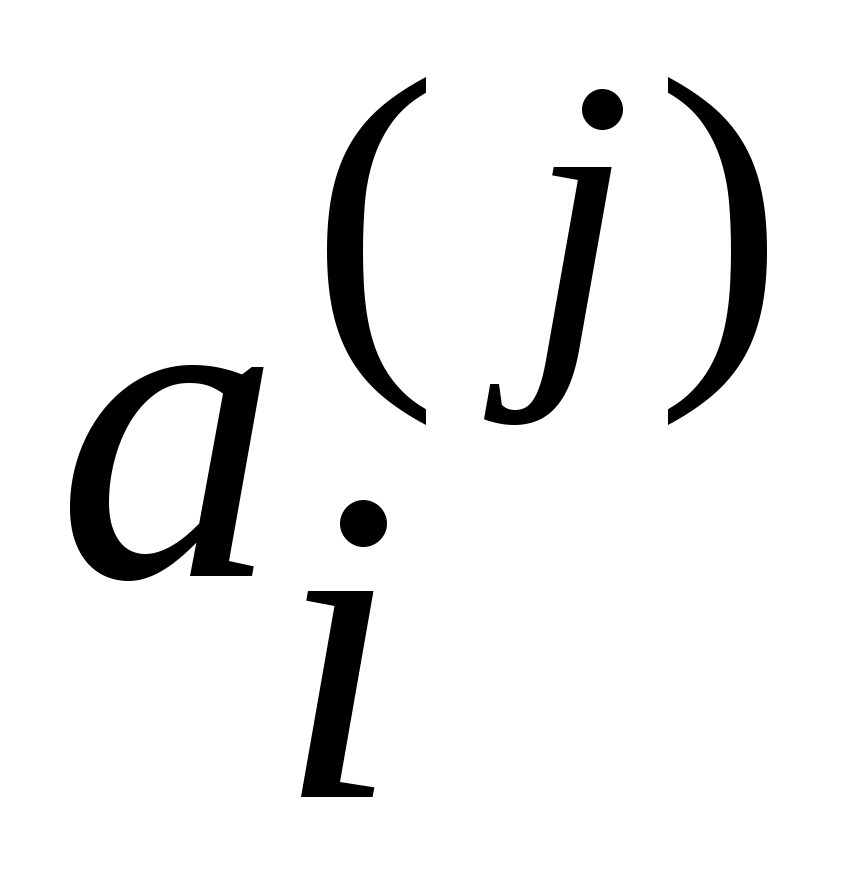 арқылы белгілейік, яғни арқылы белгілейік, яғни 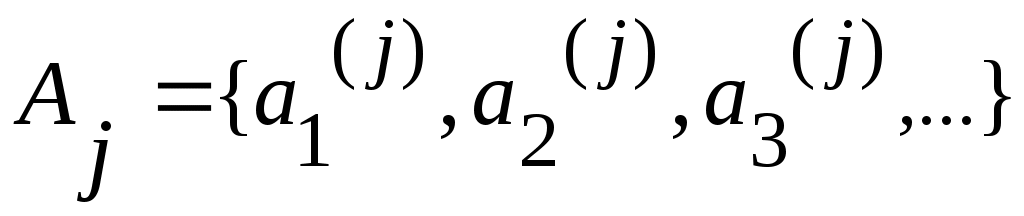 болсын. болсын.
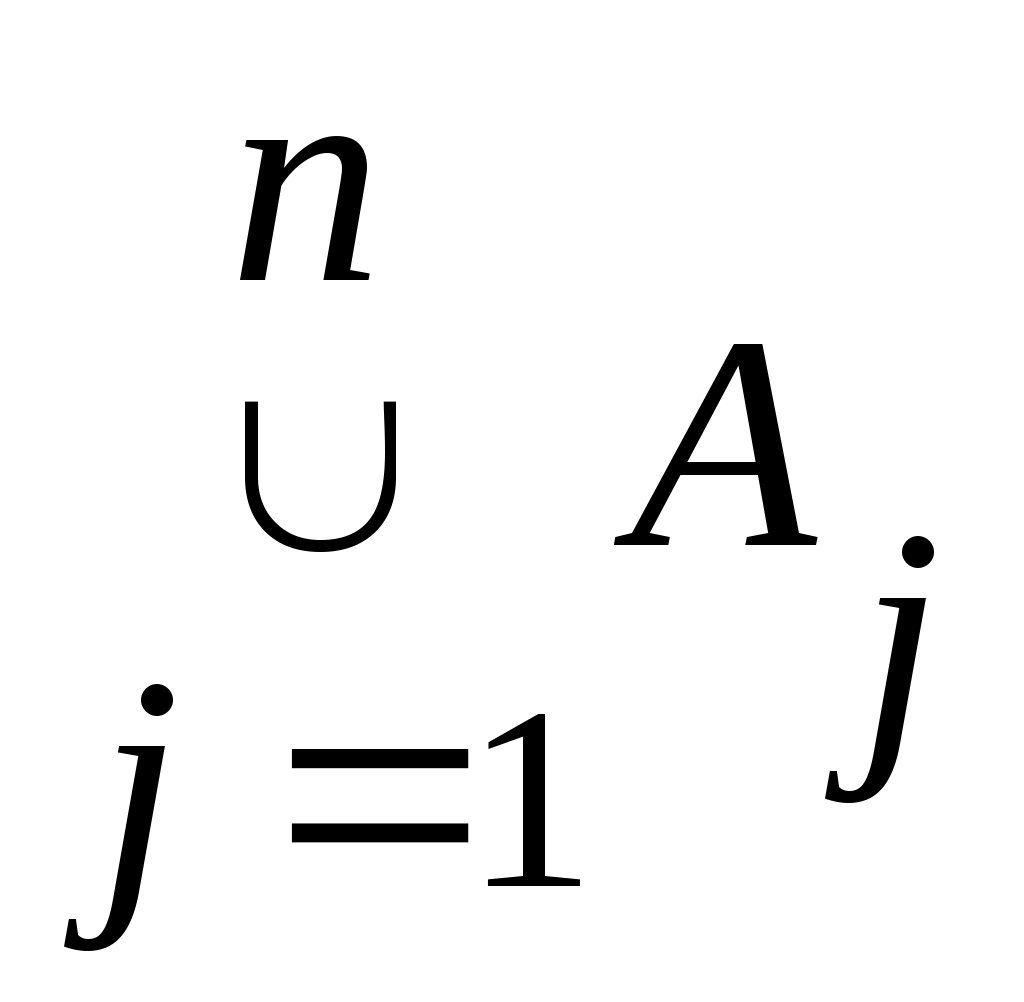 жиыны жиыны 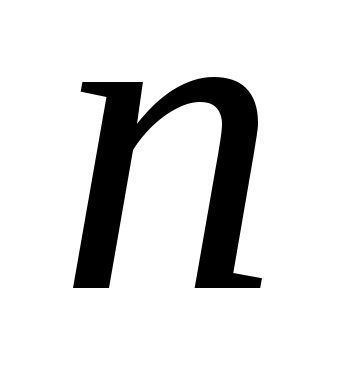 элементті, өзара қиылыспайтын элементті, өзара қиылыспайтын 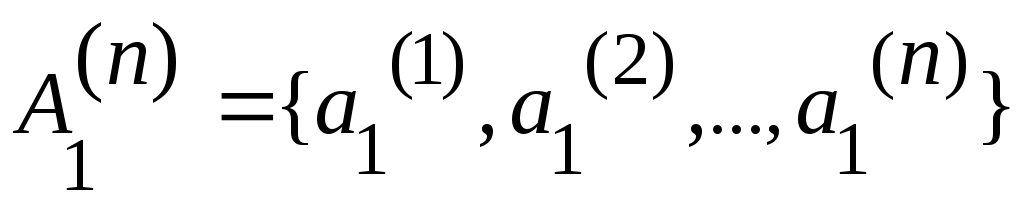 , , 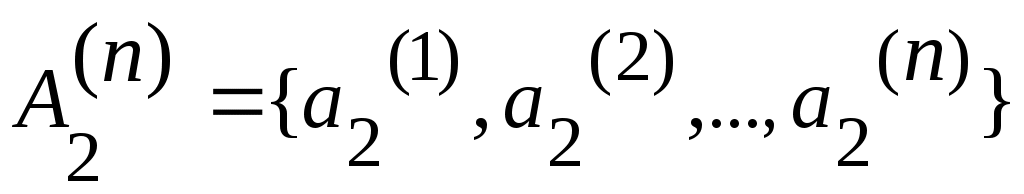 ,..., ,..., 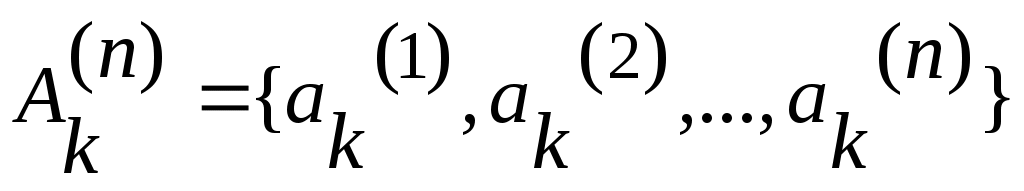 ,... жиындарының саналымды бірігуі болады. Ендеше, 3 – теорема бойынша ,... жиындарының саналымды бірігуі болады. Ендеше, 3 – теорема бойынша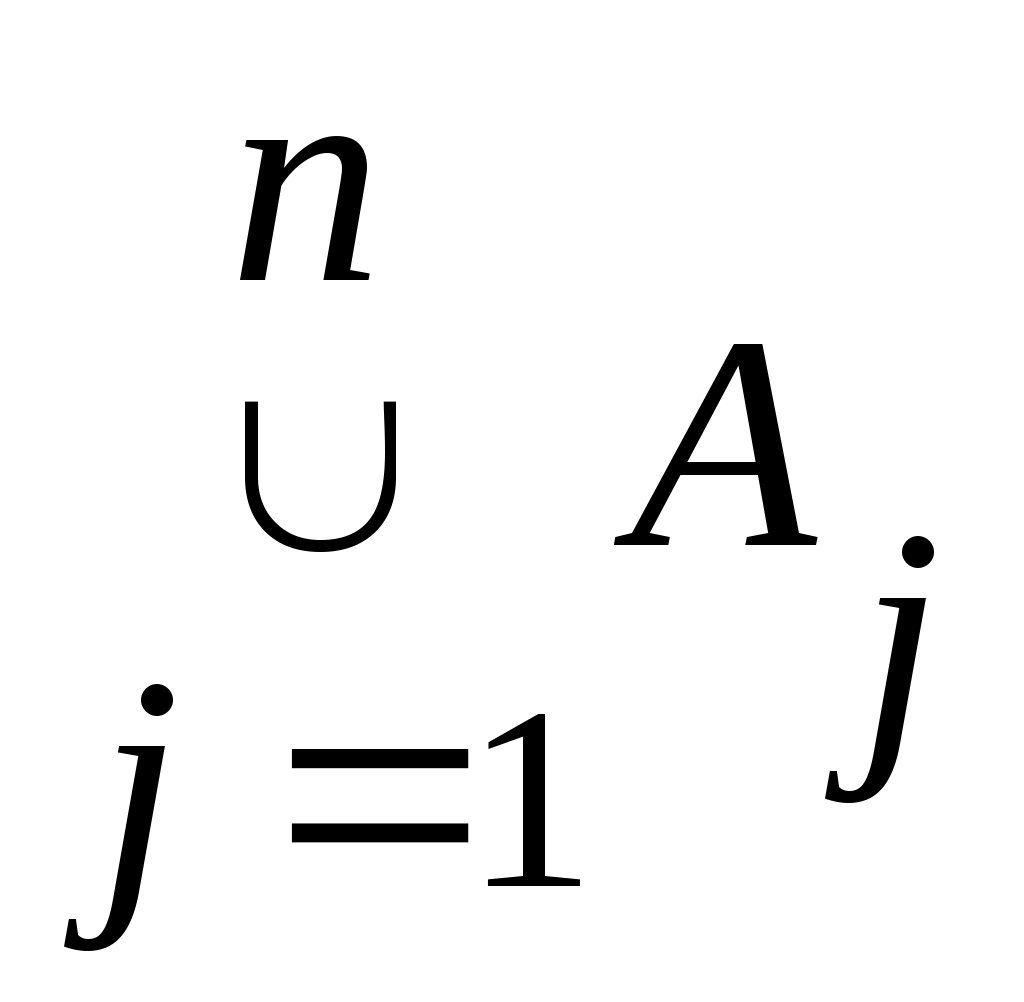 жиыны – саналымды жиын. жиыны – саналымды жиын.
4 – теорема былай да айтылады: Өзара қиылыспайтын саналымды жиын – дардың ақырлы бірігуі – саналымды жиын.
5 – теорема. Егер саналымды 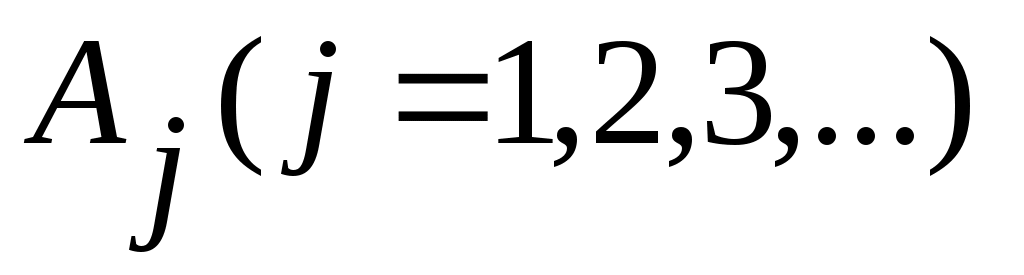 жиындары өзара қиылыс – пайтын болса, онда жиындары өзара қиылыс – пайтын болса, онда 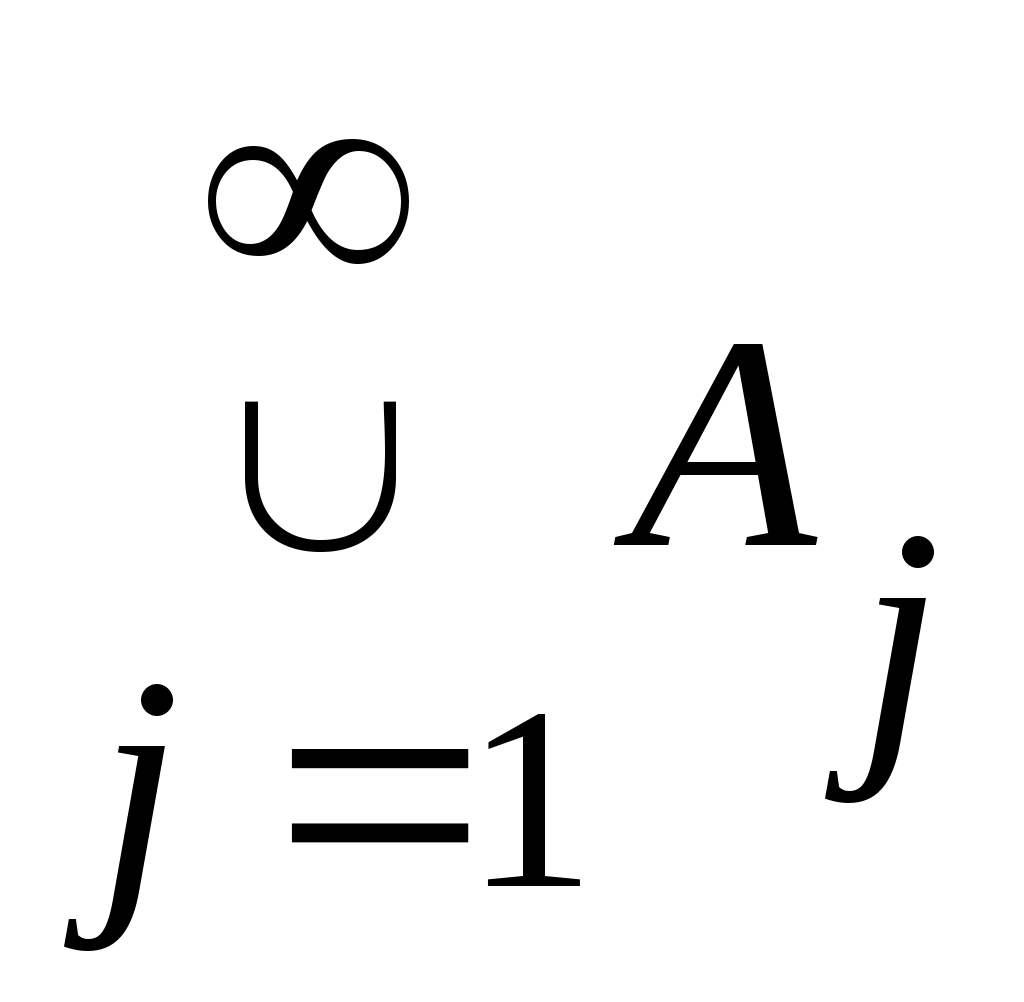 жиыны саналымды жиын болады. жиыны саналымды жиын болады.
Дәлелдеуі. Саналымды  жиынының жиынының 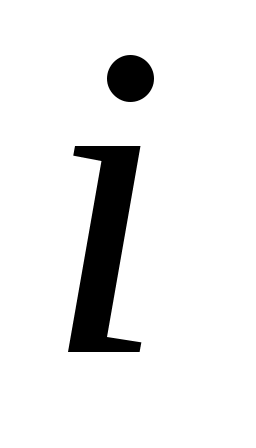 – ші нөмірге сәйкес элементін – ші нөмірге сәйкес элементін 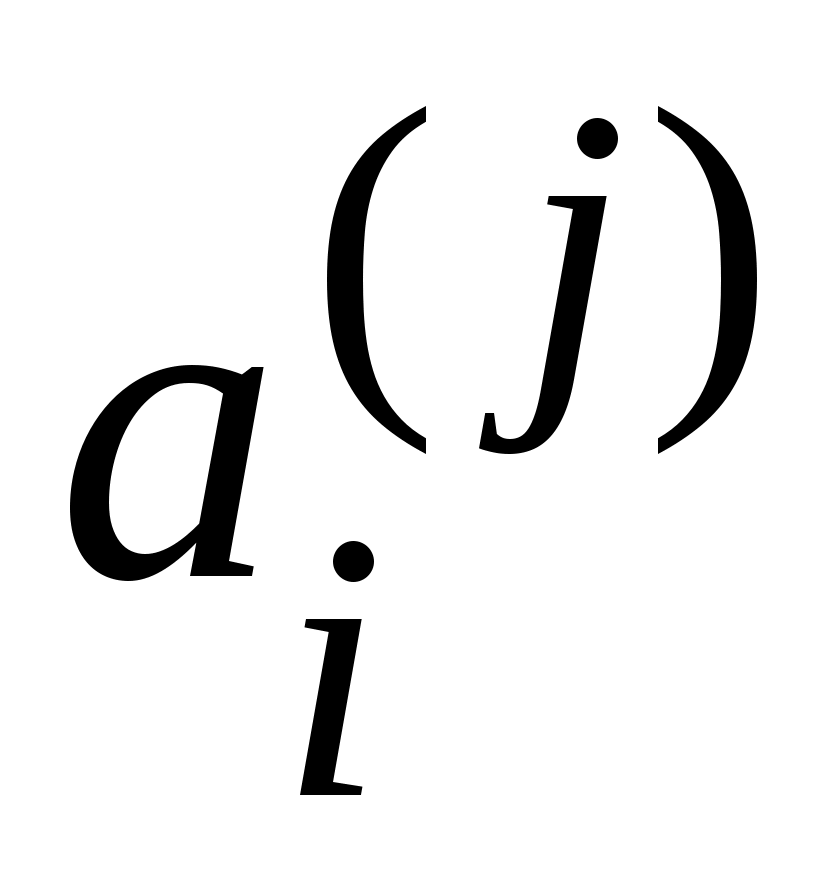 арқылы, ал жоғарғы арқылы, ал жоғарғы 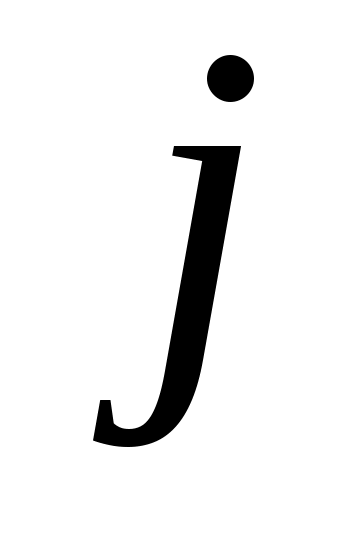 және төменгі және төменгі 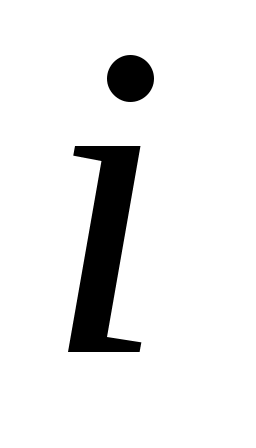 индекстерінің қосындысы индекстерінің қосындысы 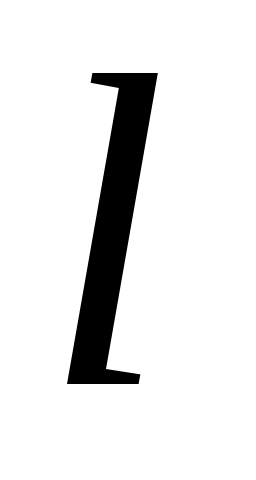 санына тең барлық санына тең барлық 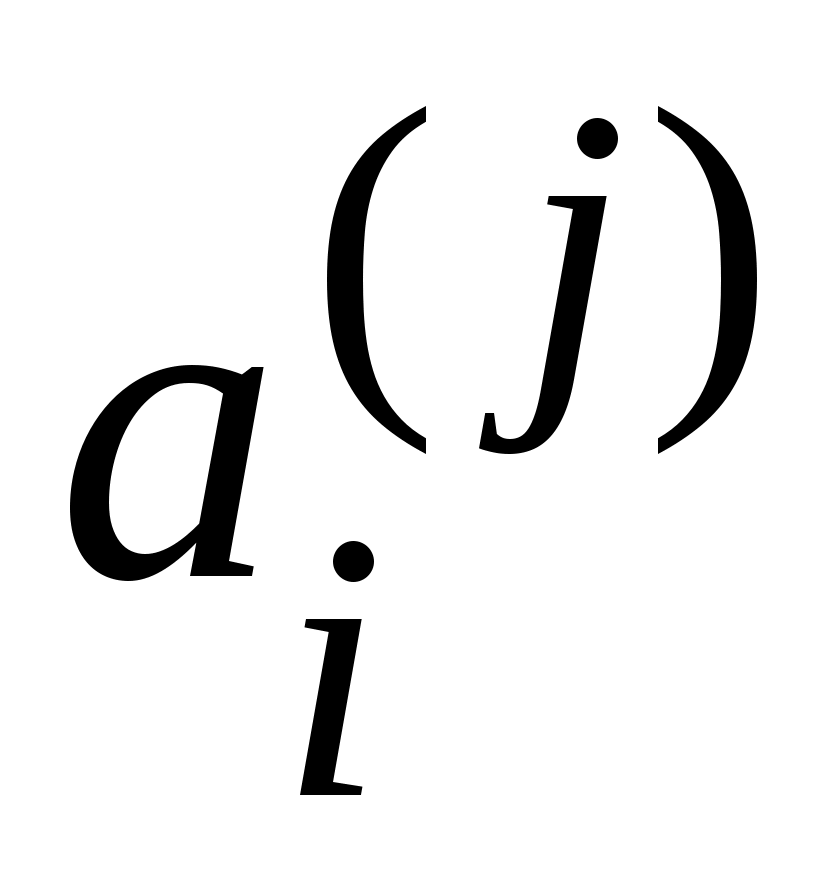 элементтерінің жиынын элементтерінің жиынын 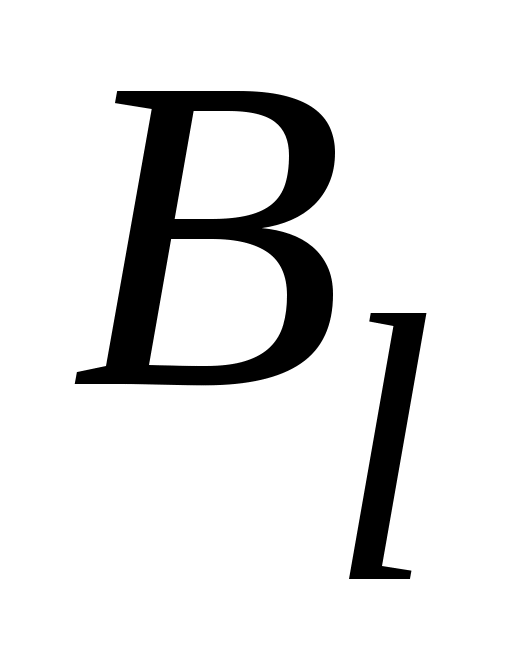 арқылы таңбалайық. арқылы таңбалайық. 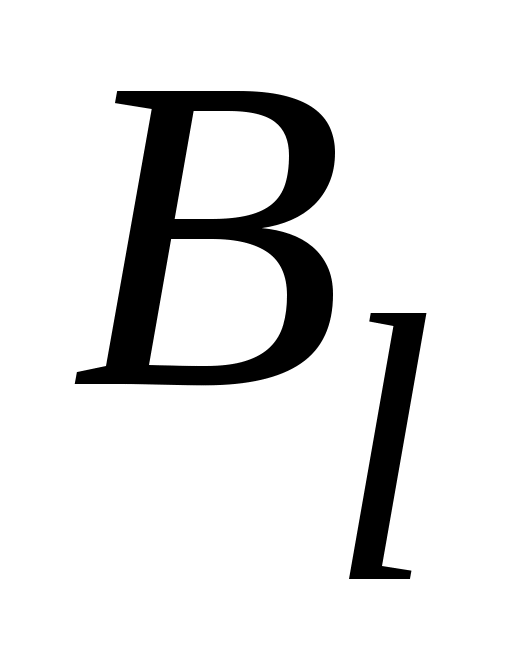 жиындары ақырлы және өзара қиылыспайды. Демек, 3 – теорема бойынша жиындары ақырлы және өзара қиылыспайды. Демек, 3 – теорема бойынша 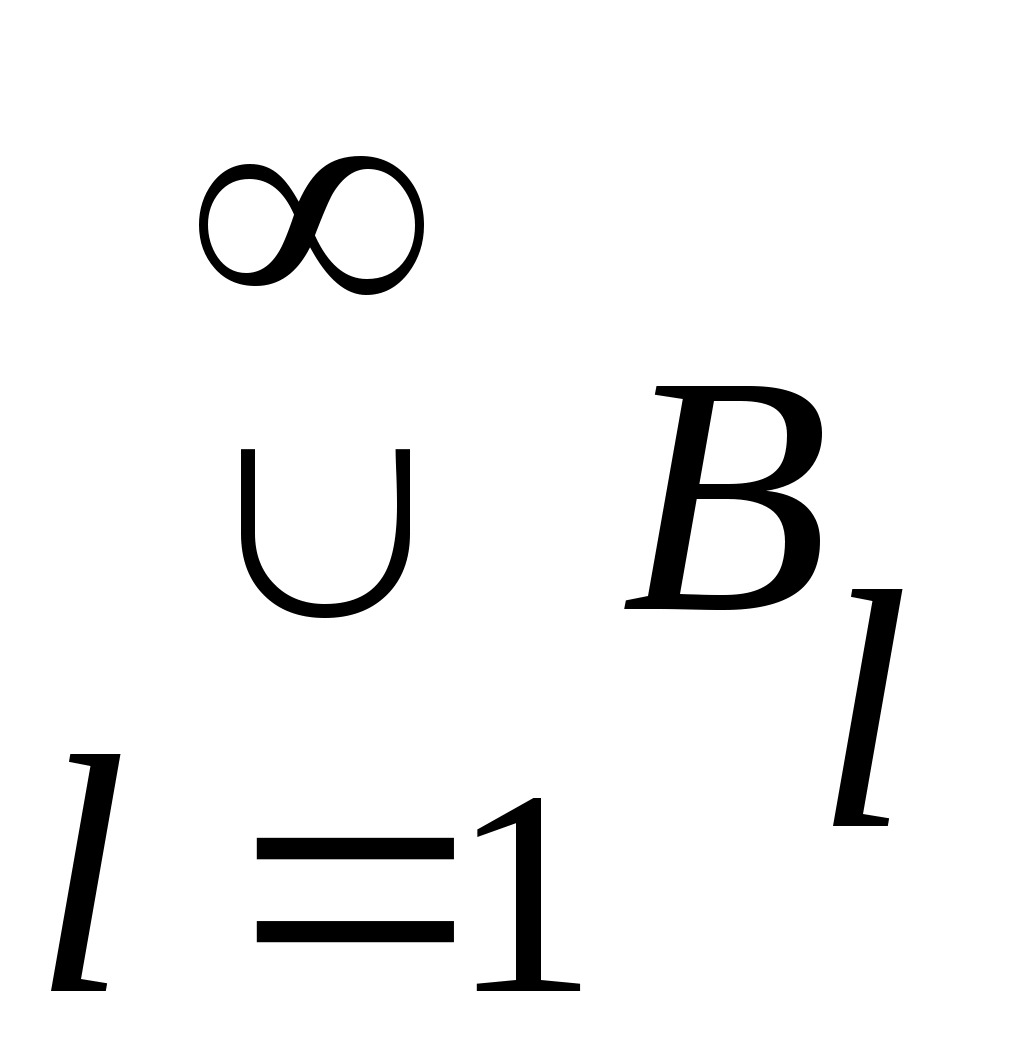 жиыны – саналымды жиын. Ендеше, жиыны – саналымды жиын. Ендеше, 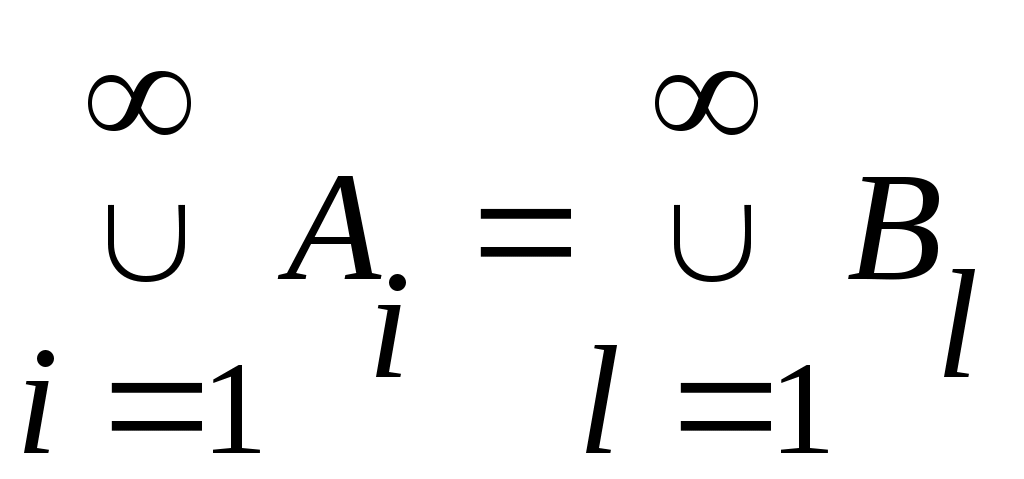 теңдігіне жүгініп, « теңдігіне жүгініп, «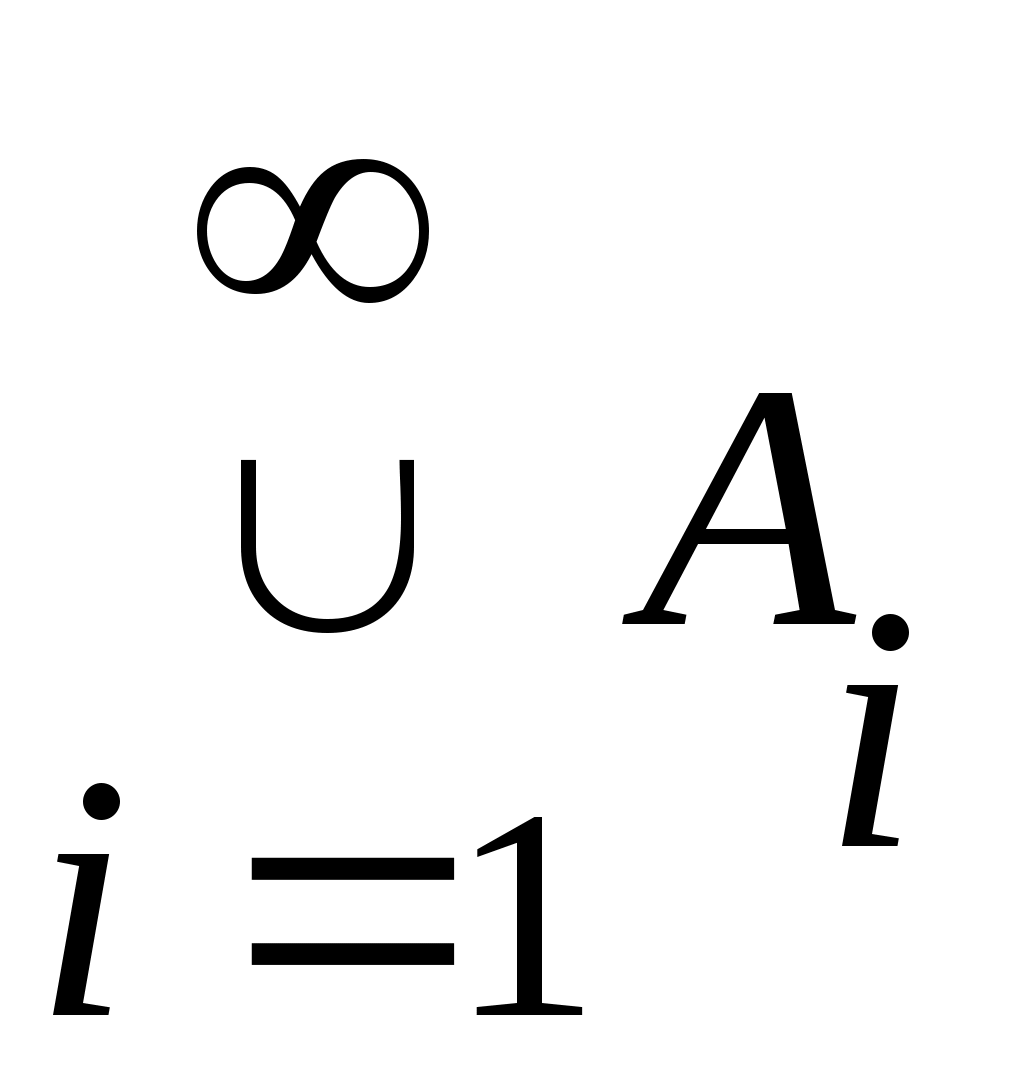 жиыны саналымды жиын» деген қорытындыға келеміз. жиыны саналымды жиын» деген қорытындыға келеміз.
5 – теорема былай да айтылады: Өзара қиылыспайтын саналымды жиын – дардың саналымды бірігуі – саналымды жиын.
6 – теорема. Әрбір ақырсыз 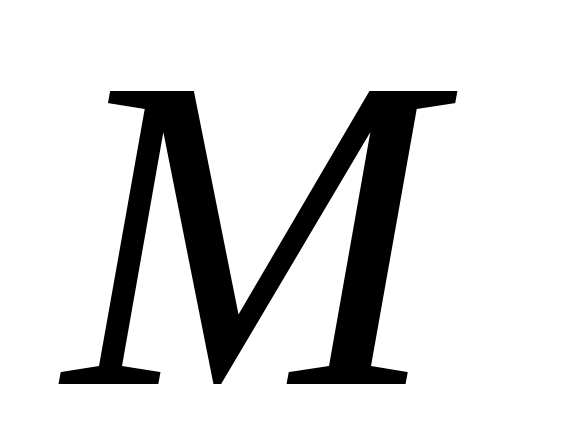 жиынының саналымды жиыншасы бар болады. жиынының саналымды жиыншасы бар болады.
Дәлелдеуі. 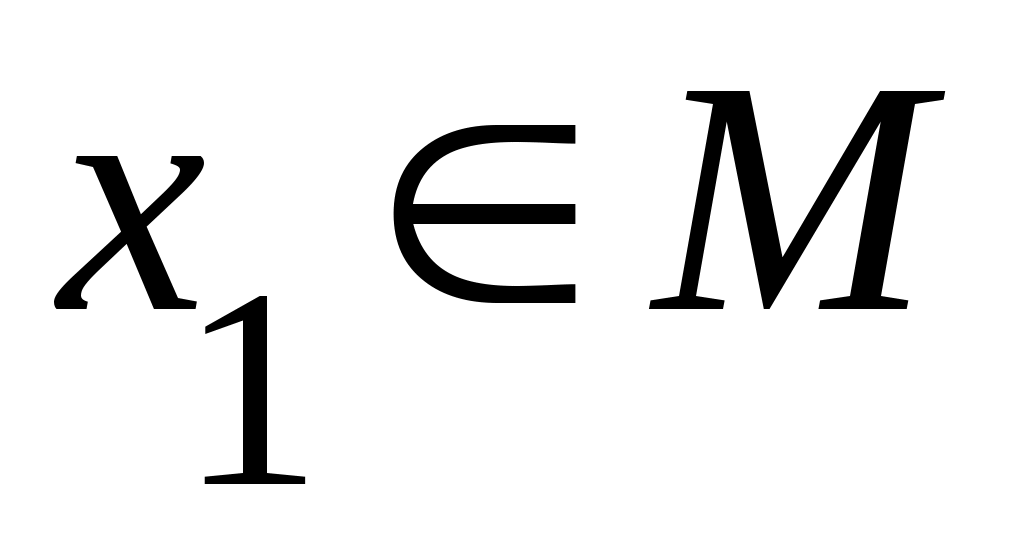 және және 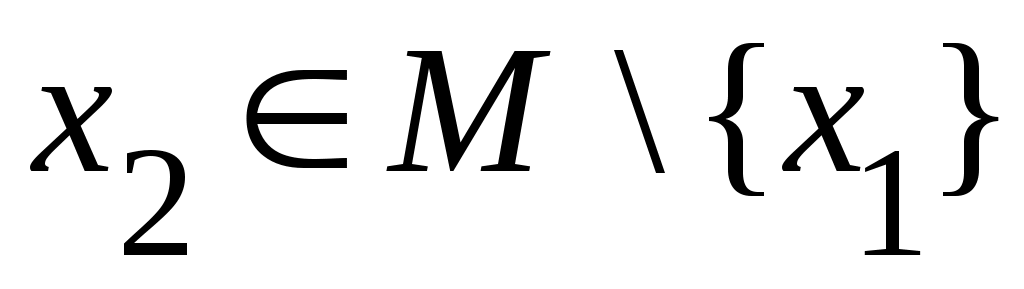 болсын. Әрбір болсын. Әрбір 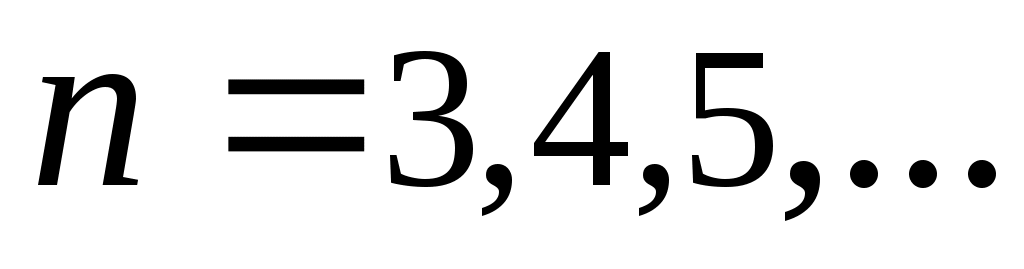 үшін үшін 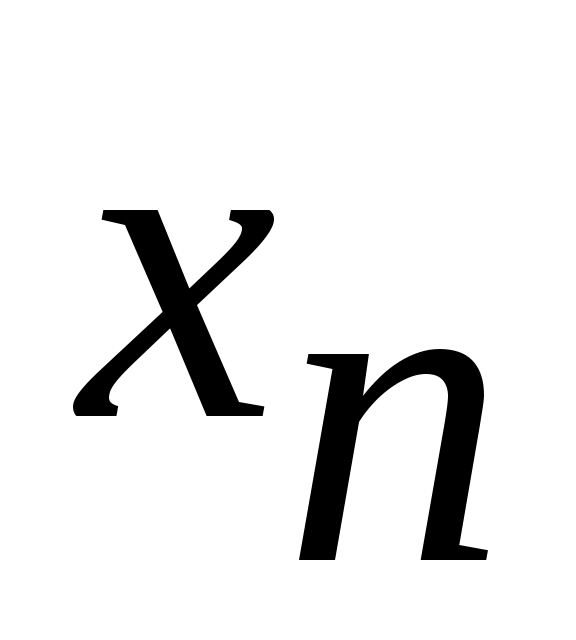
арқылы 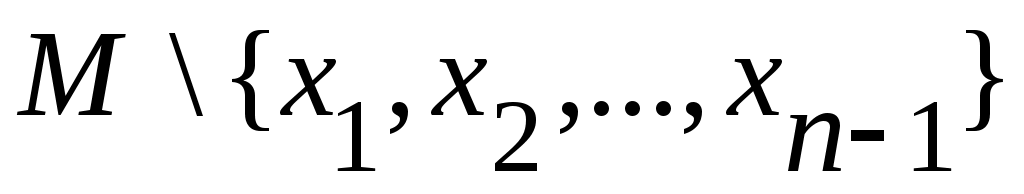 жиынының элементін белгілеп, жиынының элементін белгілеп, 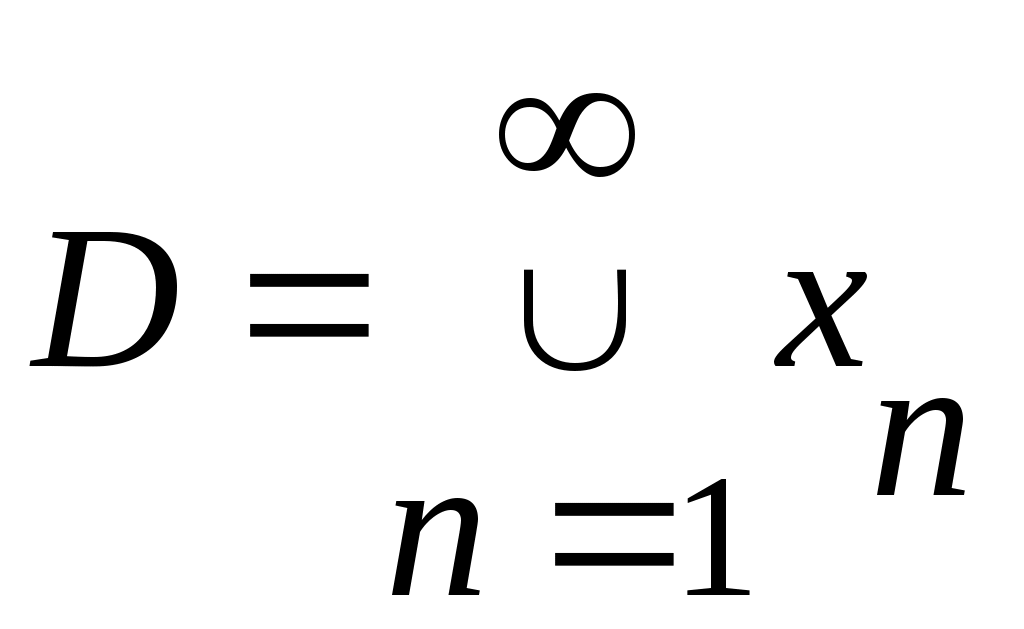 жиынын қарастырсақ, теорема дәлелдеуін аламыз, өйткені, жиынын қарастырсақ, теорема дәлелдеуін аламыз, өйткені, 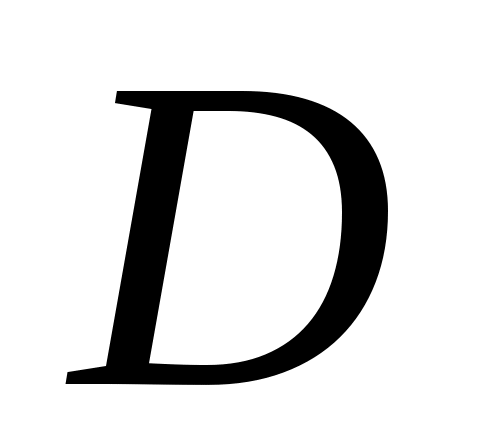 жиыны біріншіден, жиыны біріншіден, 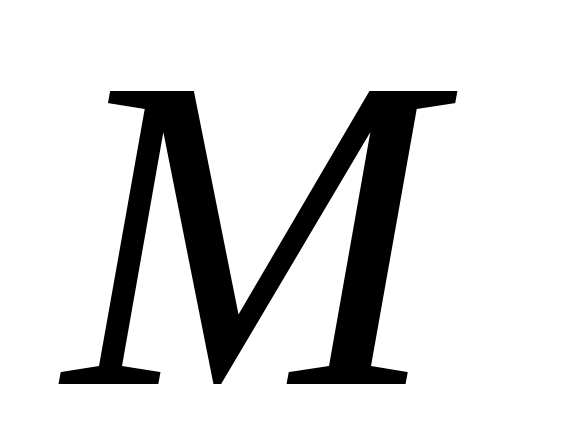 жиынының жиыншасы; екіншіден, бір элементті жиынының жиыншасы; екіншіден, бір элементті 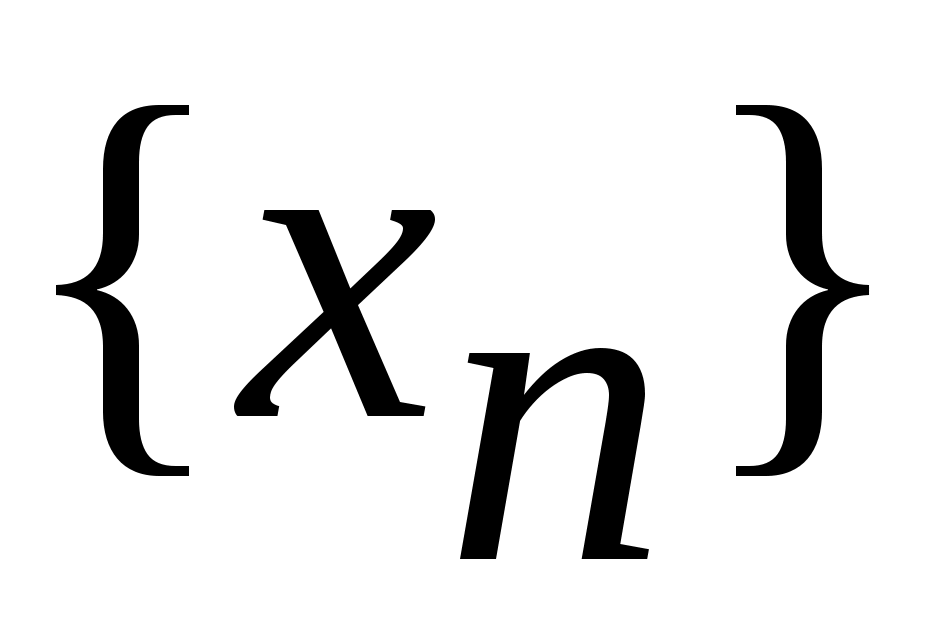 жиын – дарының саналымды бірігуі ретінде 3 – теорема бойынша саналымды жиын. жиын – дарының саналымды бірігуі ретінде 3 – теорема бойынша саналымды жиын.
6 – теорема былай да айтылады: Әрбір ақырсыз жиыннан саналымды жиын бөліп алуға болады.
7 – теорема. Саналымды жиынның кез келген ақырсыз жиыншасы – саналымды жиын.
Дәлелдеуі. 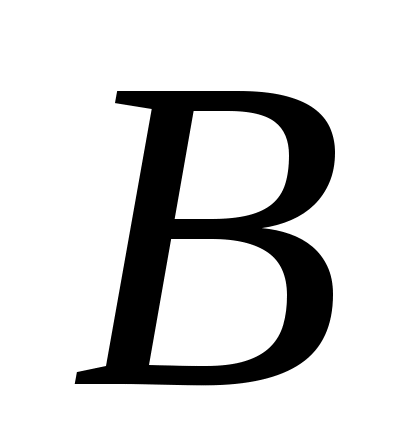 арқылы саналымды арқылы саналымды  жиынының ақырсыз жиыншасын белгілейік. 6 – теорема бойынша ақырсыз жиынының ақырсыз жиыншасын белгілейік. 6 – теорема бойынша ақырсыз 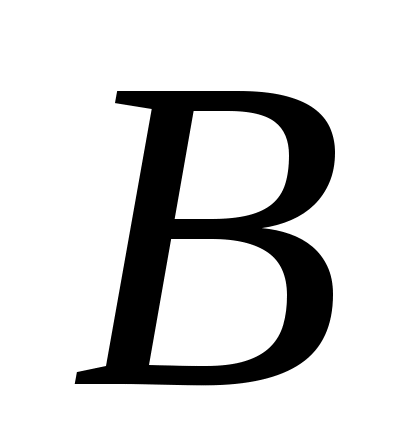 жиынынан саналымды жиынынан саналымды 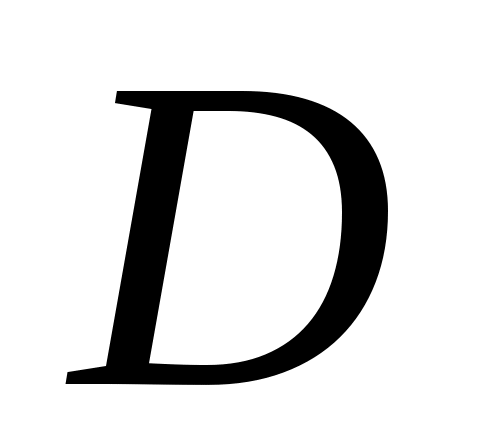 жиынын бөліп алуға болады. Әрине, жиынын бөліп алуға болады. Әрине, 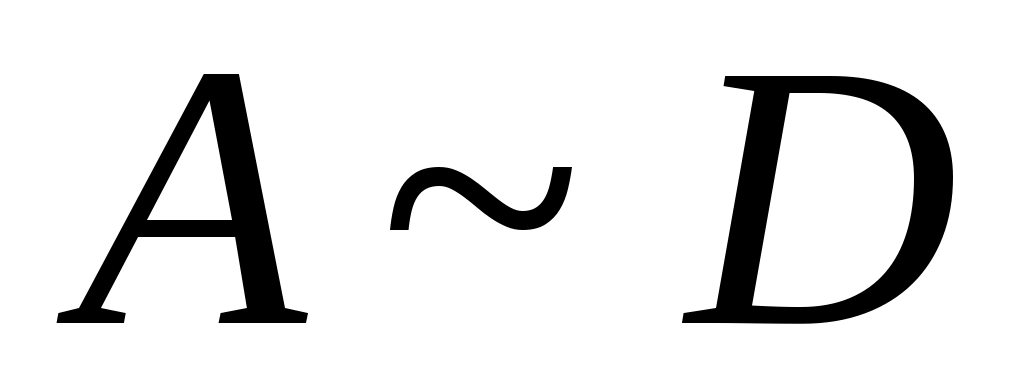 . Енді . Енді 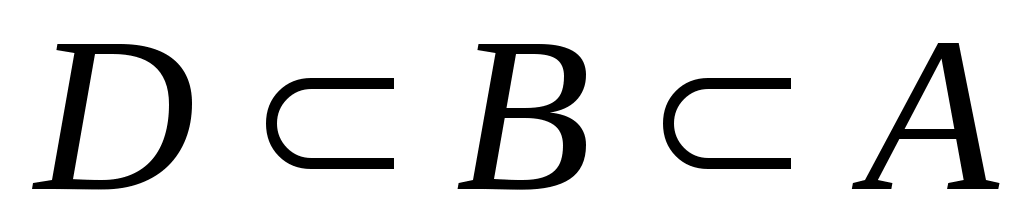 кірістірулерін ескеріп, 3– теореманы (§2) қолдансақ, кірістірулерін ескеріп, 3– теореманы (§2) қолдансақ, 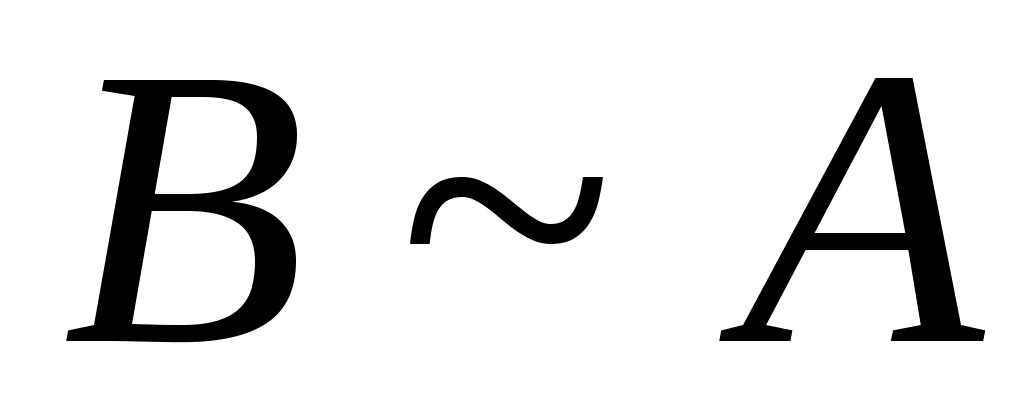 эквиваленттілігін аламыз. эквиваленттілігін аламыз.
8 – теорема. Ақырсыз 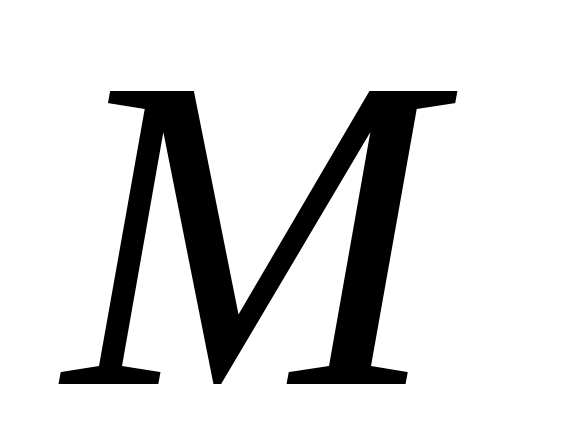 жиыны мен ақырлы немесе саналымды жиыны мен ақырлы немесе саналымды  жиыны үшін жиыны үшін 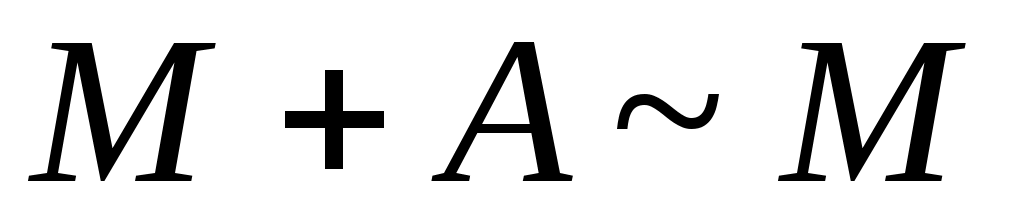 болады. болады.
Дәлелдеуі. Теорема дәлелдеуін 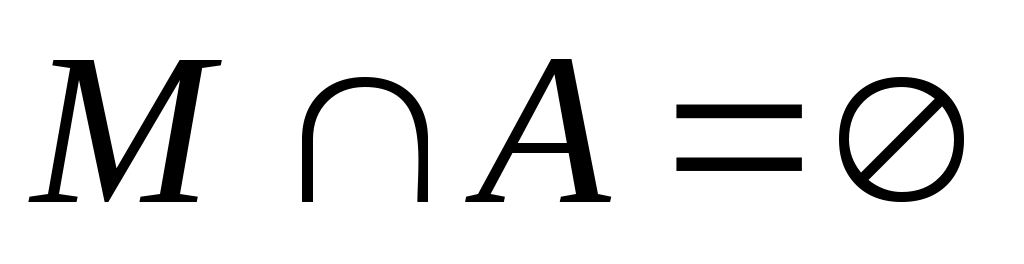 жағдайында жүргізейік. 6 – теорема бойынша ақырсыз жағдайында жүргізейік. 6 – теорема бойынша ақырсыз 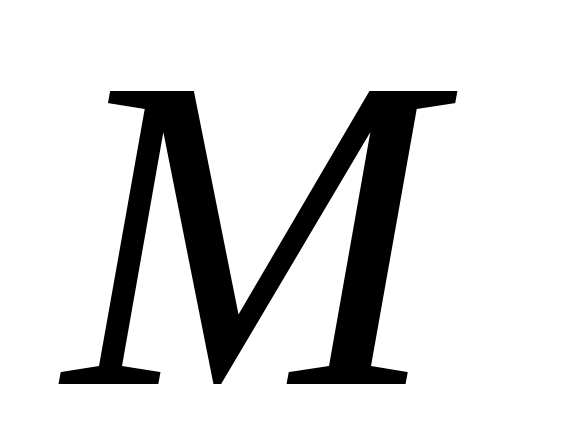 жиынынан саналымды жиынынан саналымды 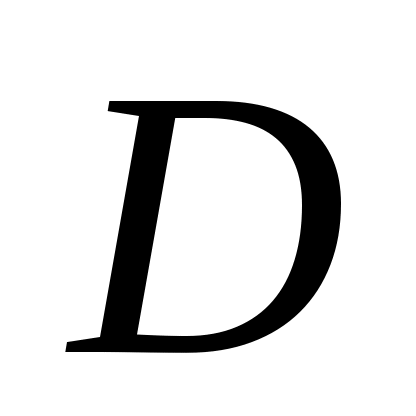 жиынын бөліп алуға болады. 2 – ші, 4 – ші теоремалар бойынша жиынын бөліп алуға болады. 2 – ші, 4 – ші теоремалар бойынша 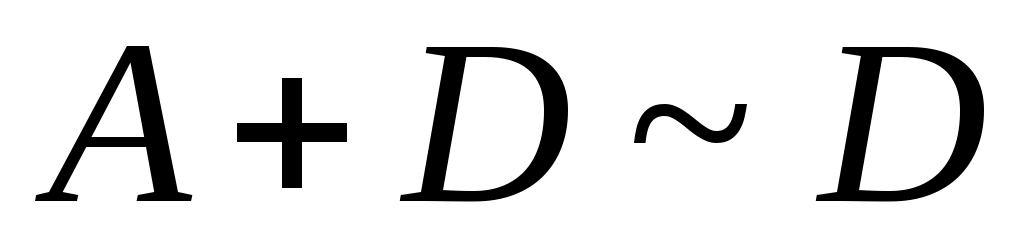 . . 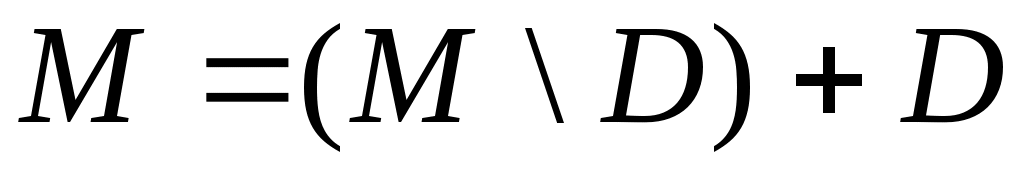 және және 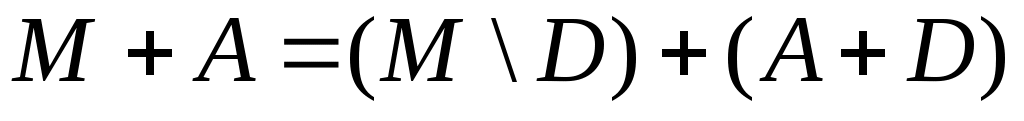 теңдіктерінің оң жақтарына зер салайық: теңдіктерінің оң жақтарына зер салайық: 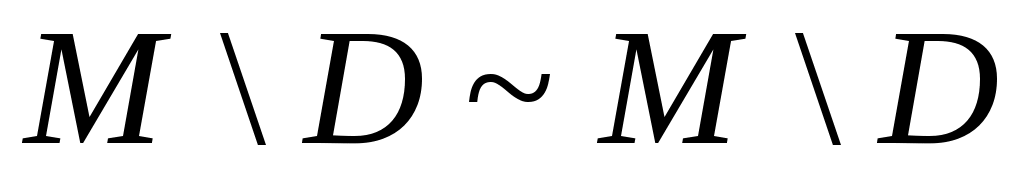 және және 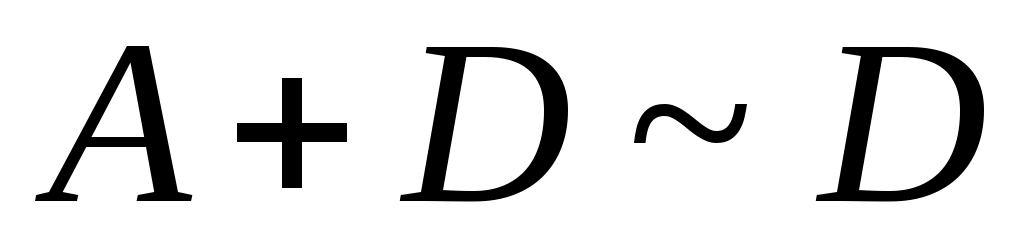 . .
Ендеше, 2– теорема (§2) бойынша 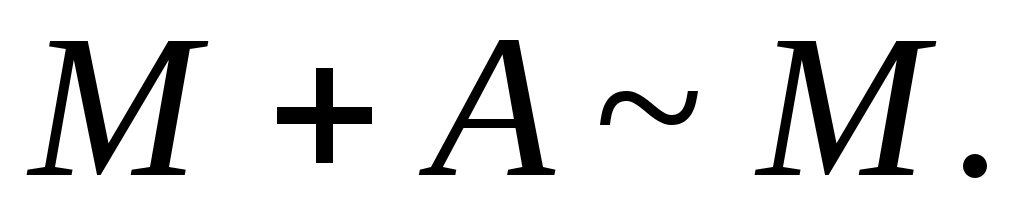 
9 – теорема. Ақырсыз, саналымды емес 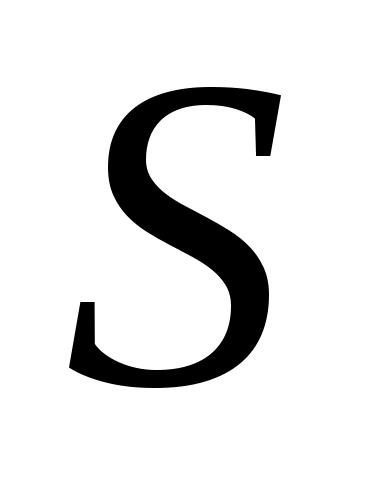 жиыны мен ақырлы немесе саналымды жиыны мен ақырлы немесе саналымды 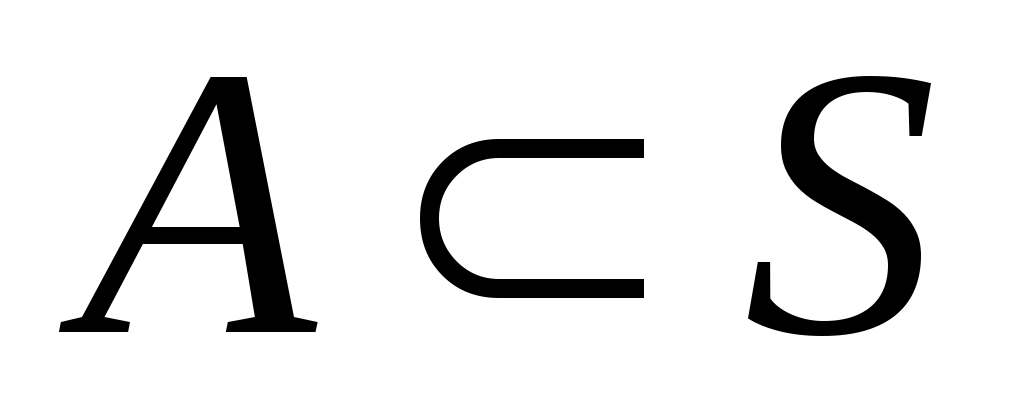 жиыншасы үшін жиыншасы үшін 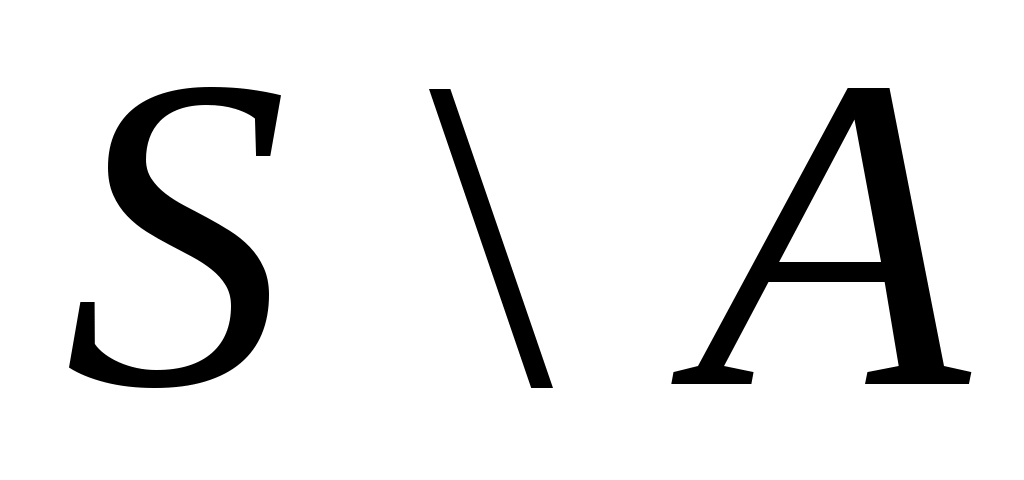 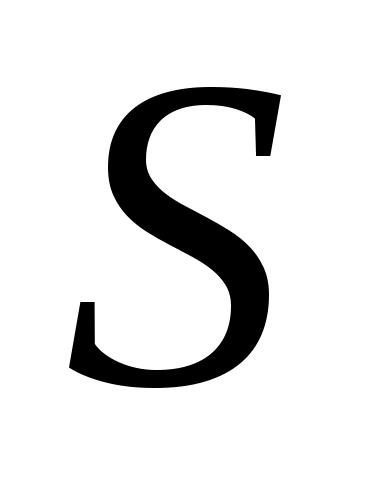 болады. болады.
Дәлелдеуі. 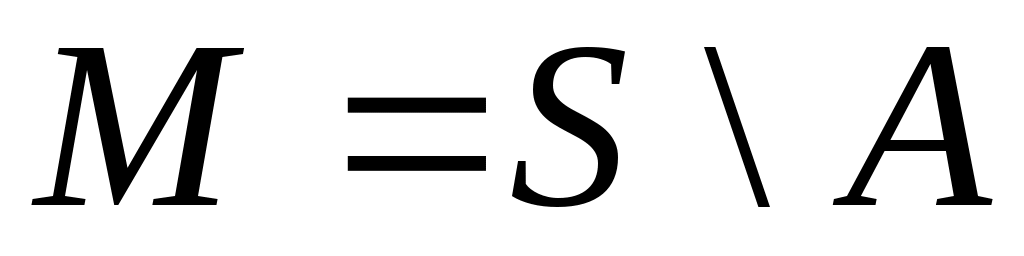 жиыны ақырсыз жиын болады, кері жағдайда жиыны ақырсыз жиын болады, кері жағдайда 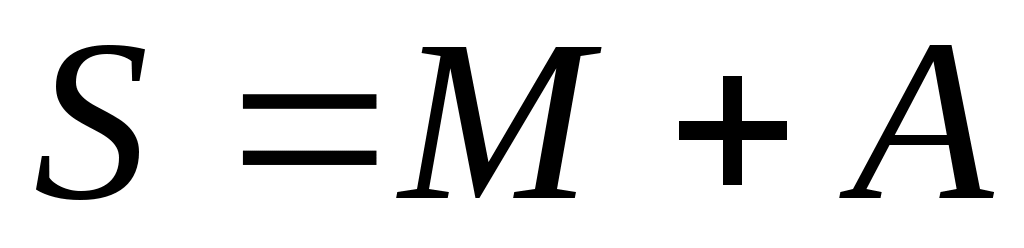 теңдігінен « теңдігінен «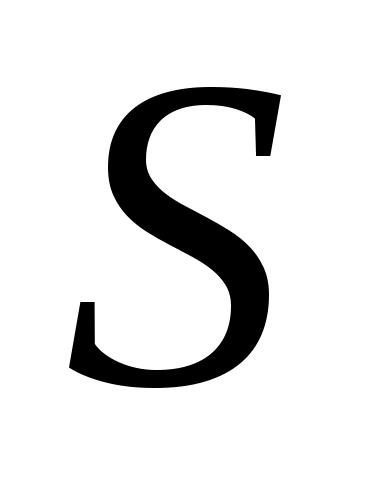 жиыны – ақырлы немесе саналымды жиын» деген қайшылыққа келер едік. 8 – теорема бойынша ақырсыз жиыны – ақырлы немесе саналымды жиын» деген қайшылыққа келер едік. 8 – теорема бойынша ақырсыз 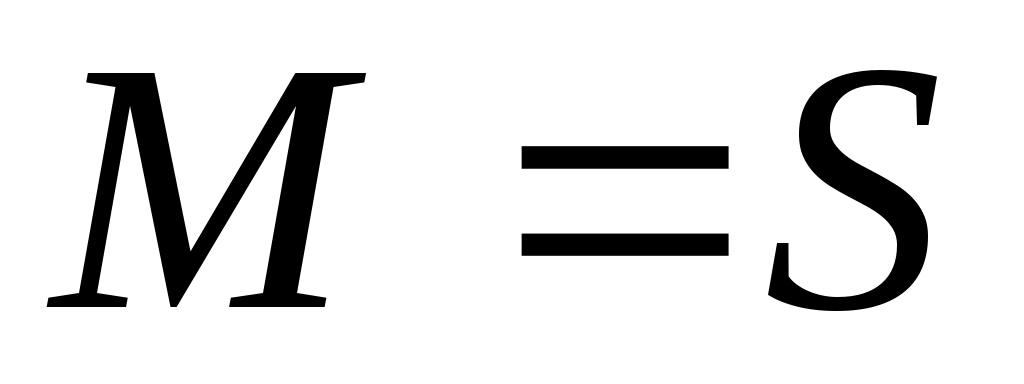 \ \ жиыны мен ақырлы немесе саналымды жиыны мен ақырлы немесе саналымды  жиыны үшін жиыны үшін 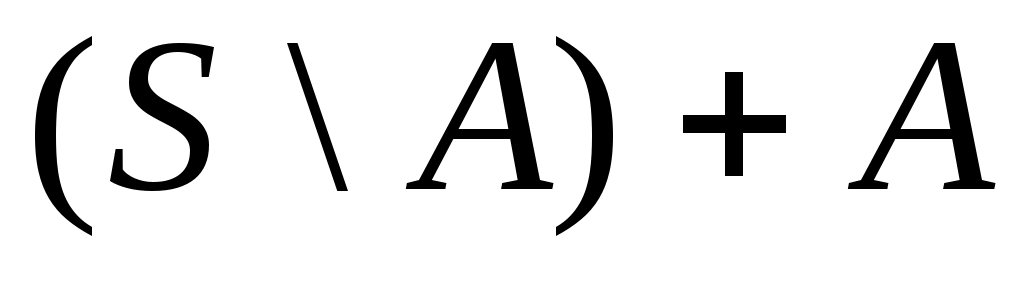
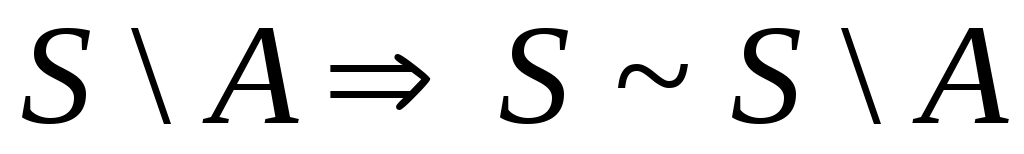 . . 3 – теореманы пайдаланып, рационал сандар жиынының саналымды жиын екеніне көз жеткізейік. 3 – теореманы пайдаланып, рационал сандар жиынының саналымды жиын екеніне көз жеткізейік.
10 – теорема. Рационал сандар жиыны – саналымды жиын.
Дәлелдеуі. Рационал сандар жиынын әдеттегідей 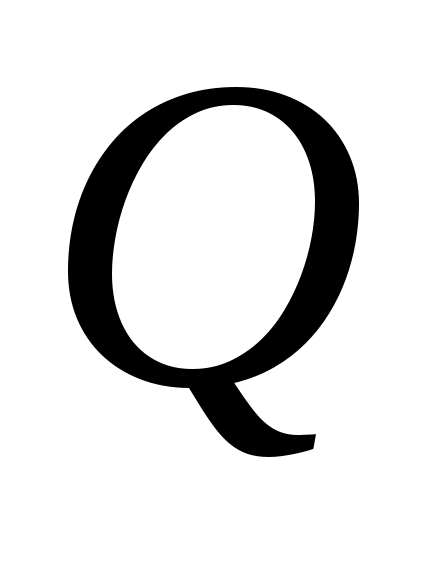 арқылы белгілейік. Ал арқылы белгілейік. Ал 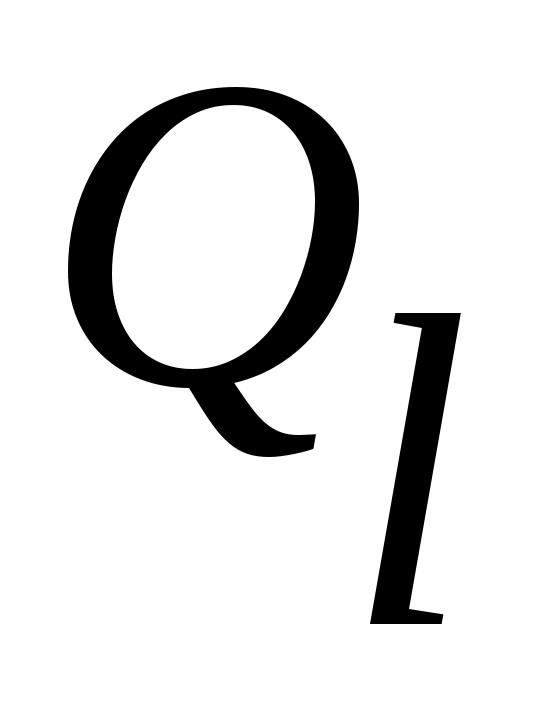 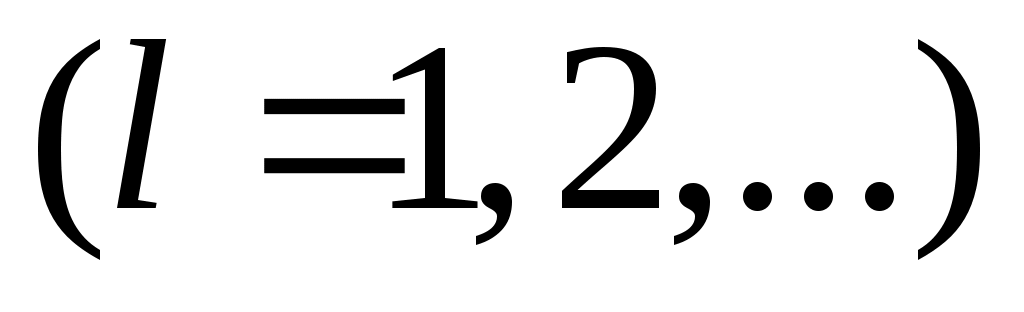 арқылы қысқартылмайтын, арқылы қысқартылмайтын, 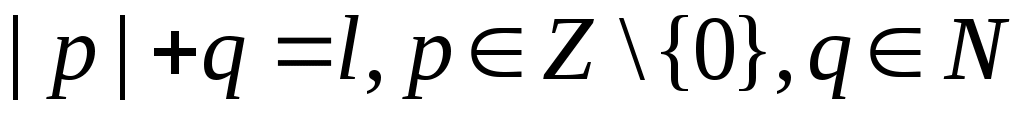 шарттарын қанағаттандыратын шарттарын қанағаттандыратын 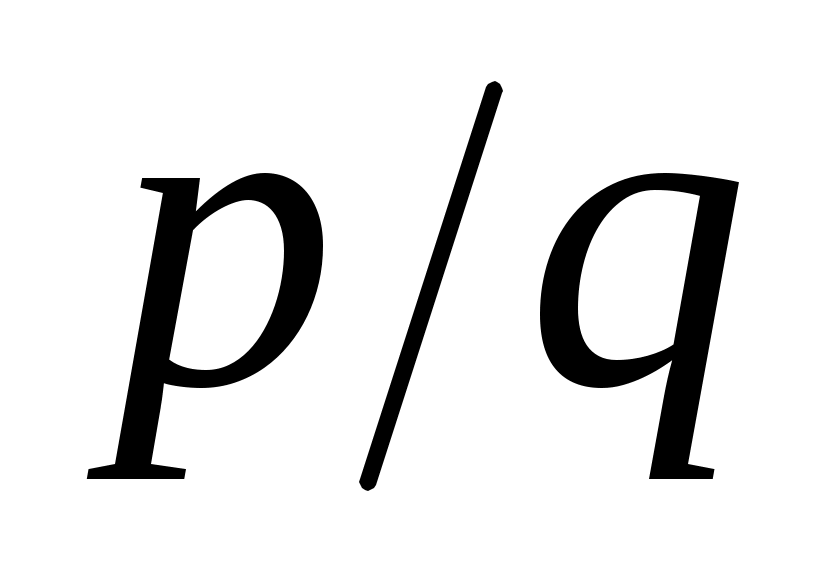 бөлшектерінің жиынын таңбалайық. бөлшектерінің жиынын таңбалайық. 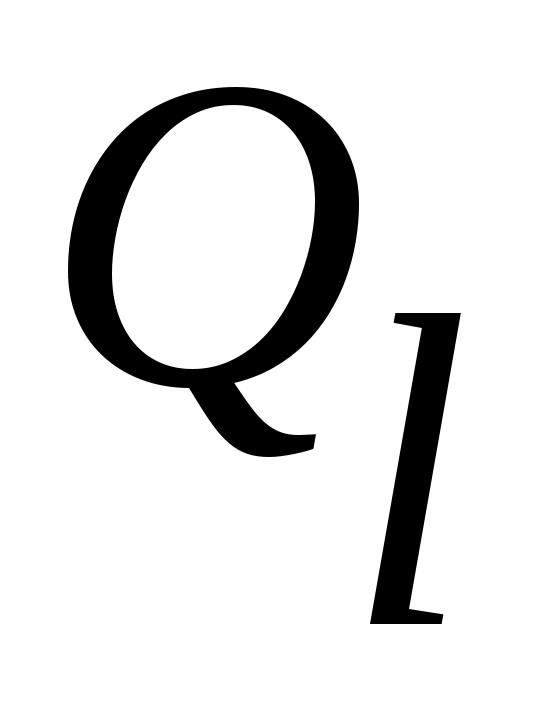 жиындары ақырлы, өзара қиылыспайды. 3 – теорема бойынша жиындары ақырлы, өзара қиылыспайды. 3 – теорема бойынша 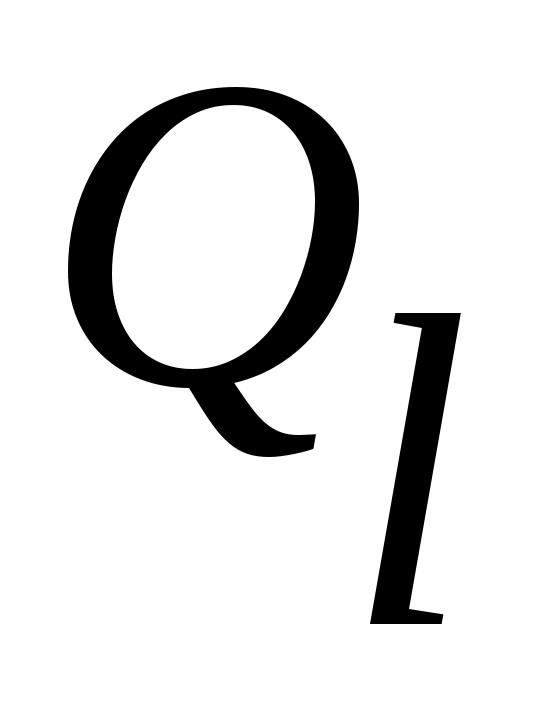 жиындарының жиындарының
саналымды бірігуі саналымды жиын болады. Ендеше, 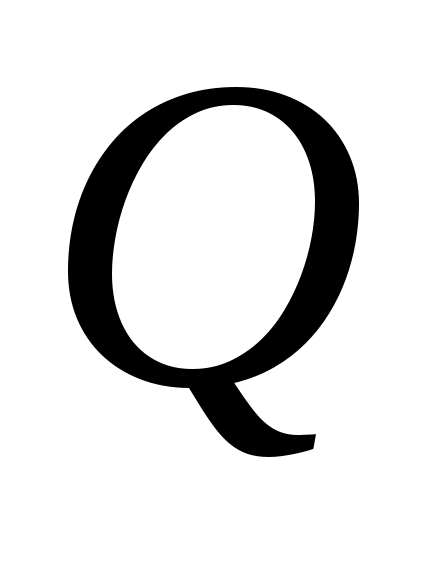 жиыны – саналымды жиын, өйткені, жиыны – саналымды жиын, өйткені, 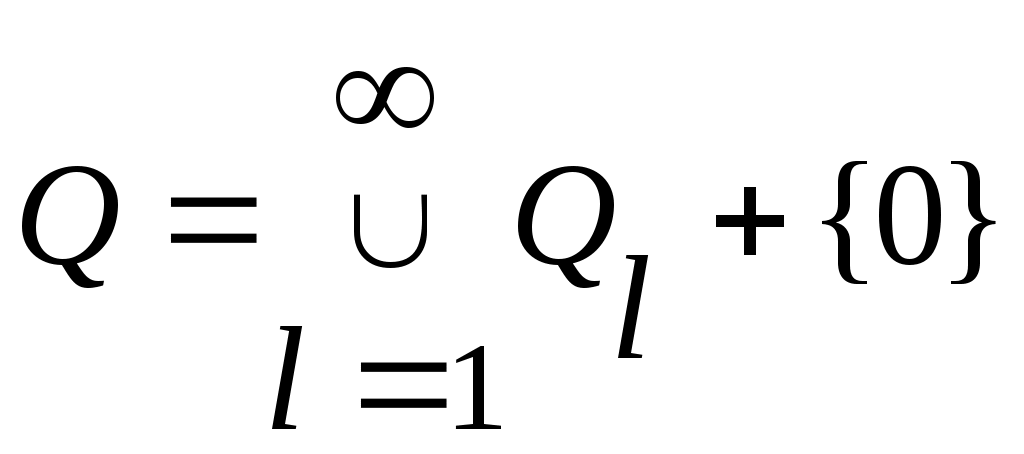 . .
2 – анықтама. 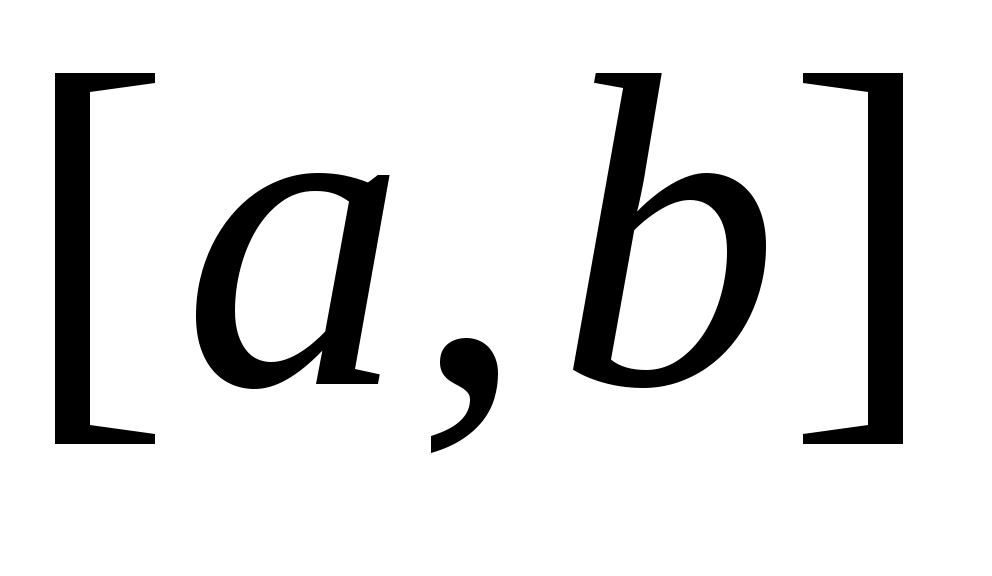 сегментінде анықталған сегментінде анықталған 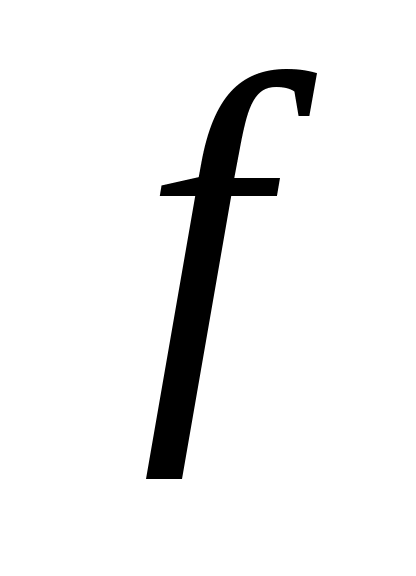 функциясы берілсін. Егер функциясы берілсін. Егер 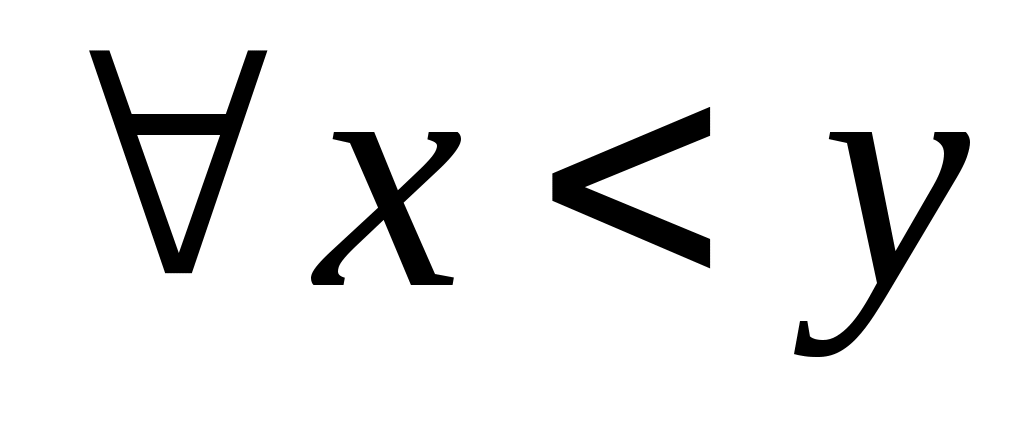 үшін үшін 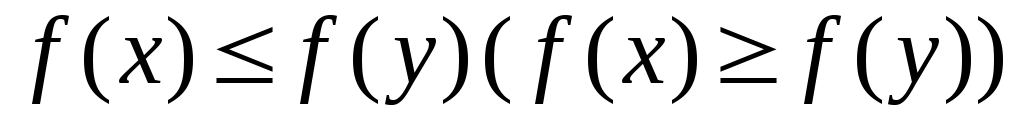 теңсіздігі орындалатын болса, онда теңсіздігі орындалатын болса, онда 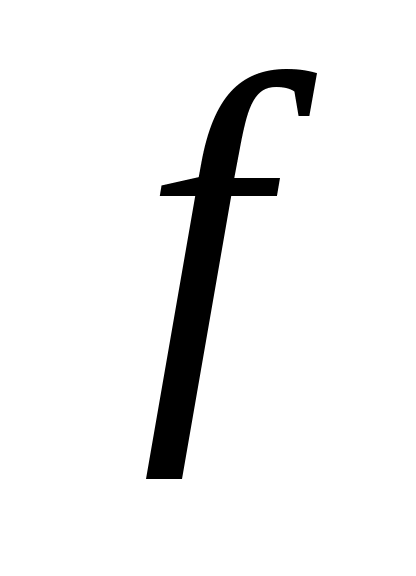 функциясы « функциясы «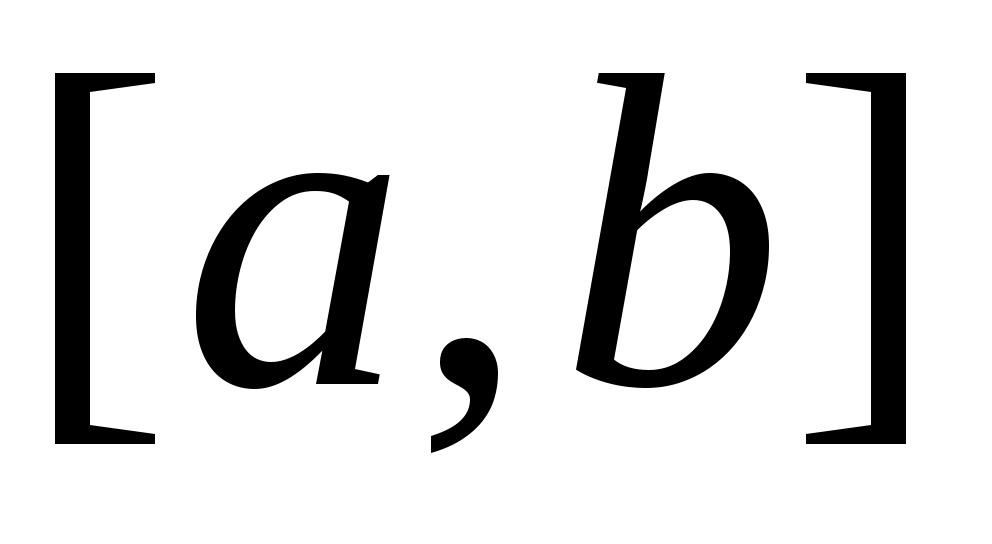 сегментінде кемімейтін (өспейтін) функция» деп аталады. Кемімейтін, өспейтін функцияның әрқайсысы «монотонды функция» деп аталады. сегментінде кемімейтін (өспейтін) функция» деп аталады. Кемімейтін, өспейтін функцияның әрқайсысы «монотонды функция» деп аталады.
11 – теорема. 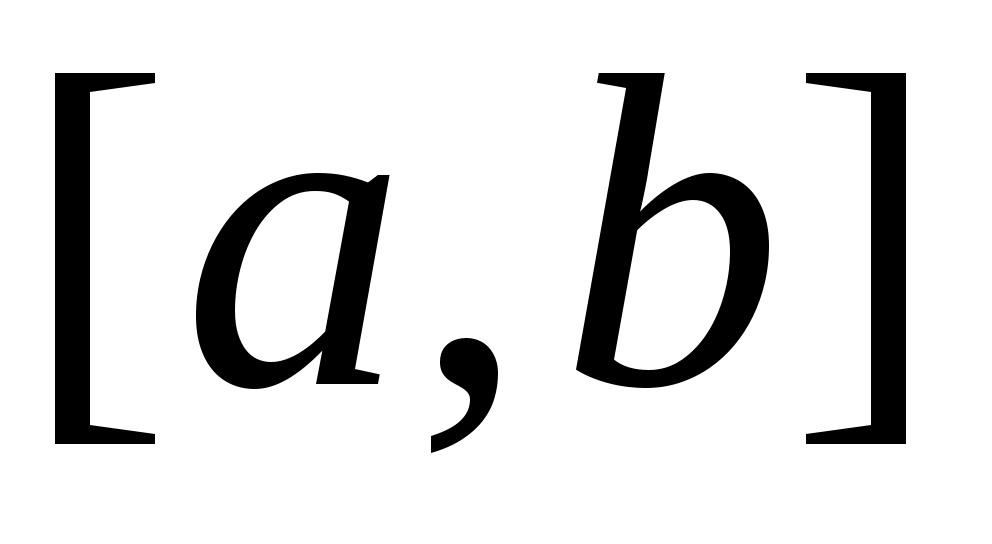 сегментінде монотонды функцияның үзіліс нүкте – лерінің жиыны ақырлы немесе саналымды жиын құрайды. сегментінде монотонды функцияның үзіліс нүкте – лерінің жиыны ақырлы немесе саналымды жиын құрайды.
Дәлелдеуі. Дәлелдеуді кемімейтін 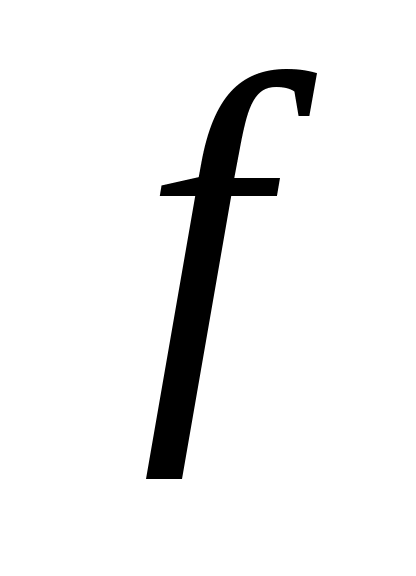 функциясы үшін жүргізейік. Әрбір функциясы үшін жүргізейік. Әрбір 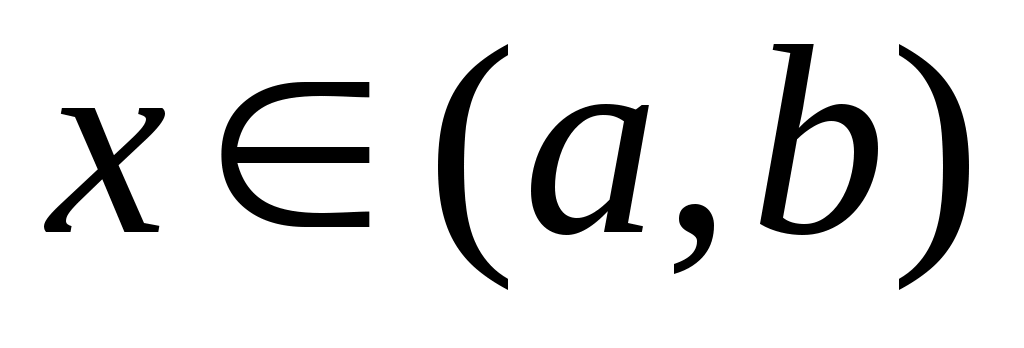 нүктесінде нүктесінде 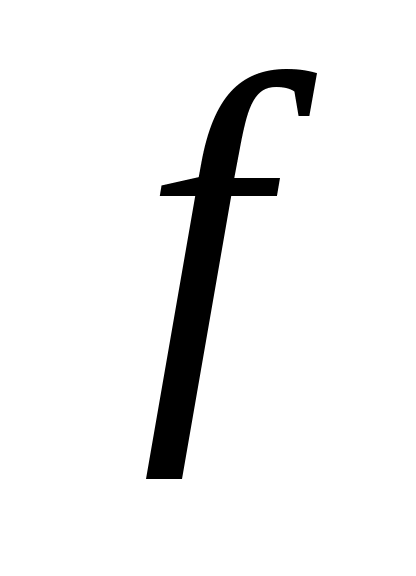 функциясының нақты мәнді оң жақты және сол жақты шектері бар болады. Бұл шектер математикалық анализде функциясының нақты мәнді оң жақты және сол жақты шектері бар болады. Бұл шектер математикалық анализде 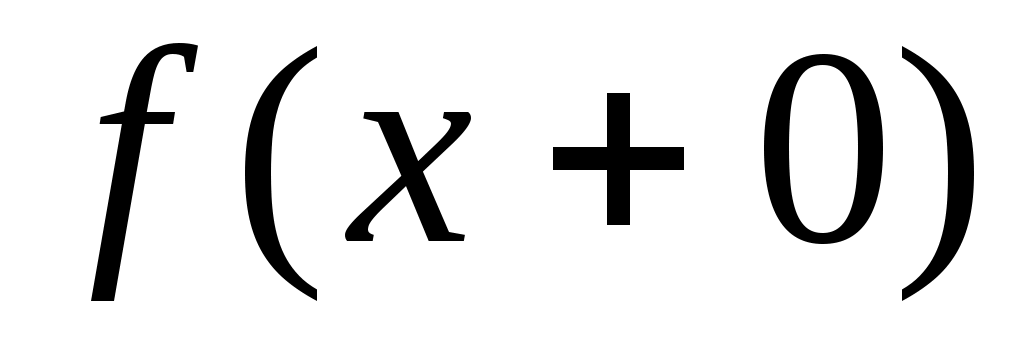 және және 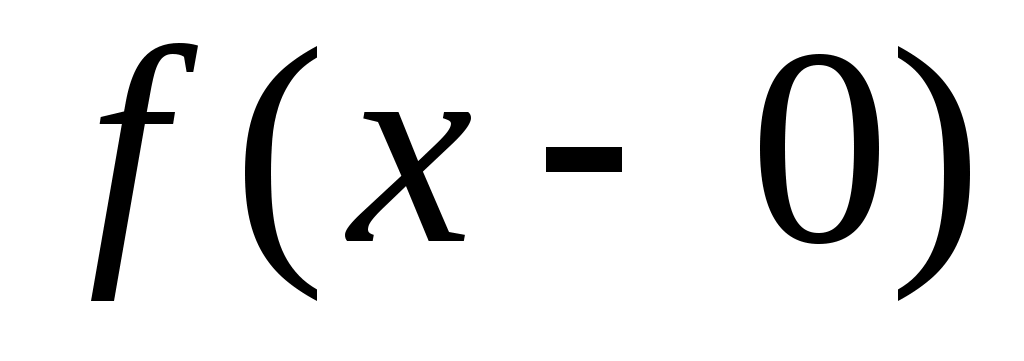 символдары арқылы белгіленген еді. символдары арқылы белгіленген еді. 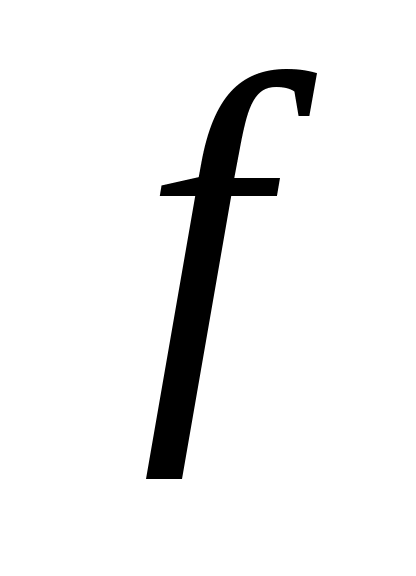 функциясының үзіліс нүктелері жиынын функциясының үзіліс нүктелері жиынын  арқылы таңбалап, арқылы таңбалап,
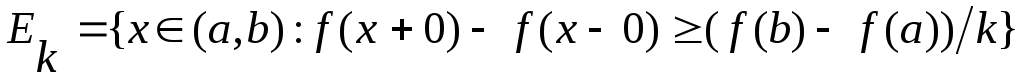 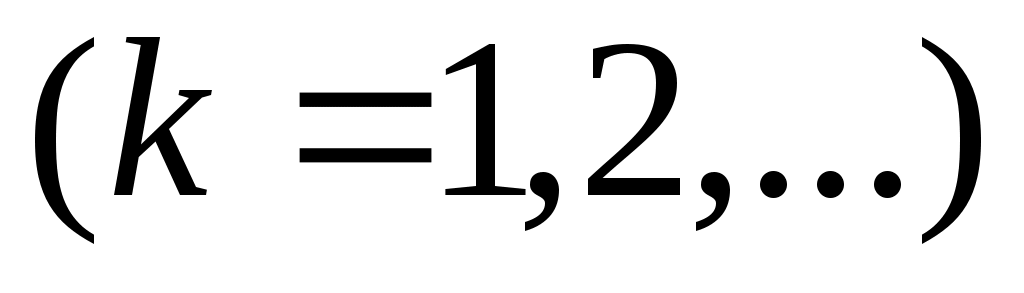
жиындарын қарастырайық.
 жиыны жиыны 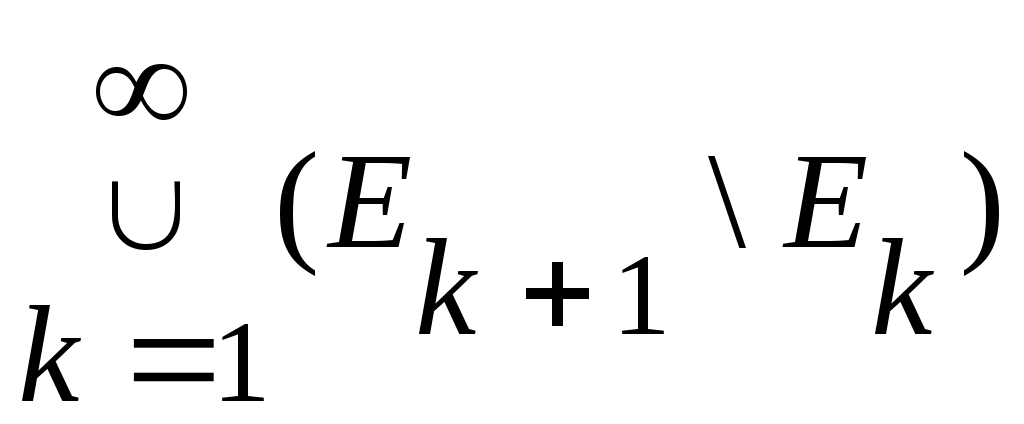 , , 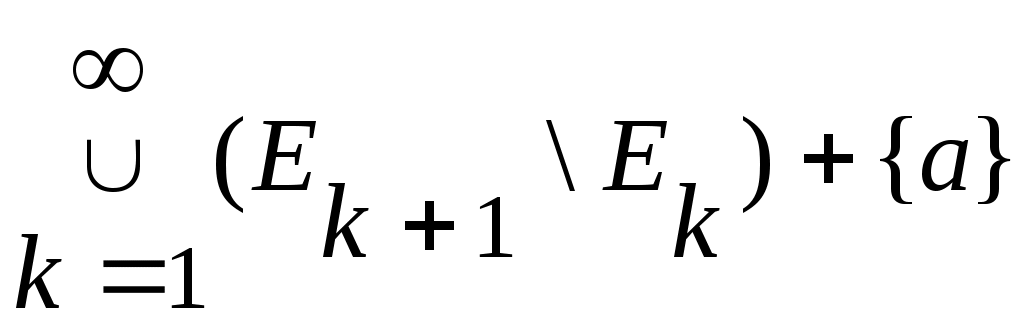 , ,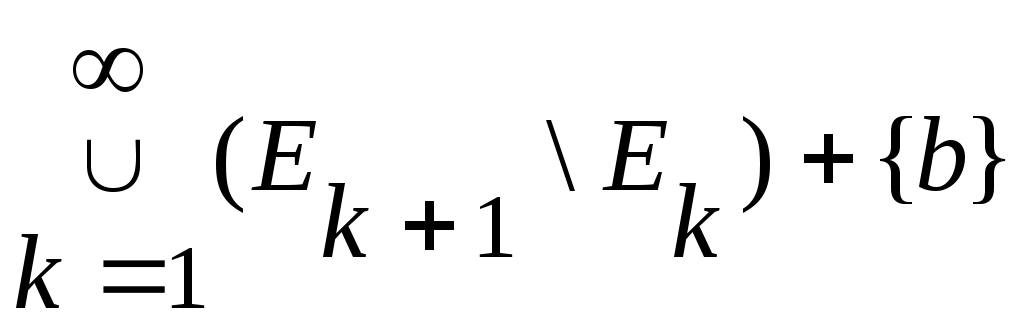 , , 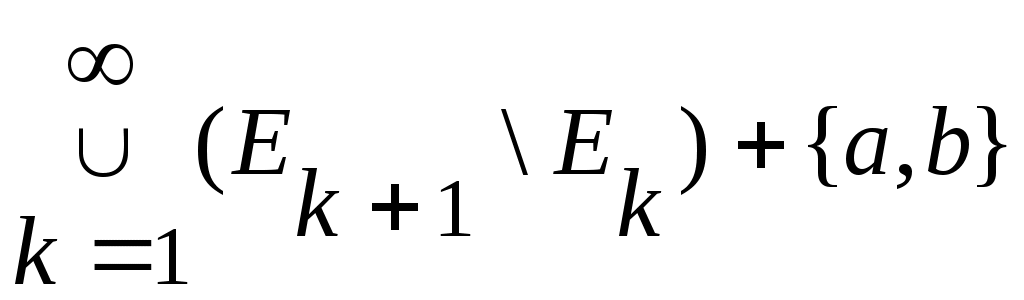 жиындарының бірімен беттеседі (Осыны тексеріңіз). жиындарының бірімен беттеседі (Осыны тексеріңіз).
Ендеше, 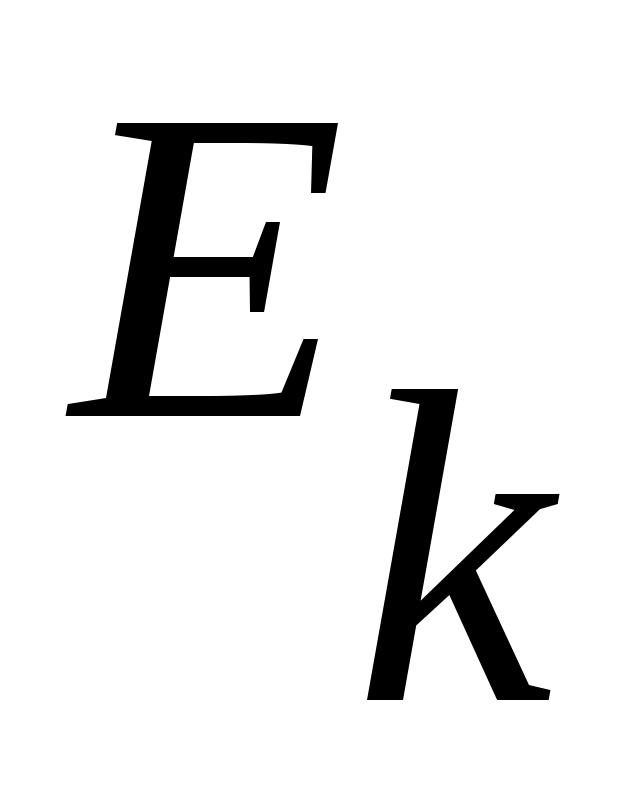 жиындарының әрқайсысы ақырлы жиын екенін ескерсек, « жиындарының әрқайсысы ақырлы жиын екенін ескерсек, « жиыны – не ақырлы, не саналымды жиын» деген қорытындыға келеміз. жиыны – не ақырлы, не саналымды жиын» деген қорытындыға келеміз.
§4. Континуалды жиындар
1 – анықтама. 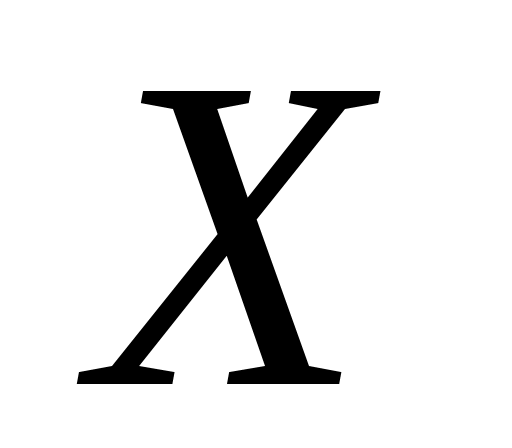 жиыны берілсін. Егер жиыны берілсін. Егер 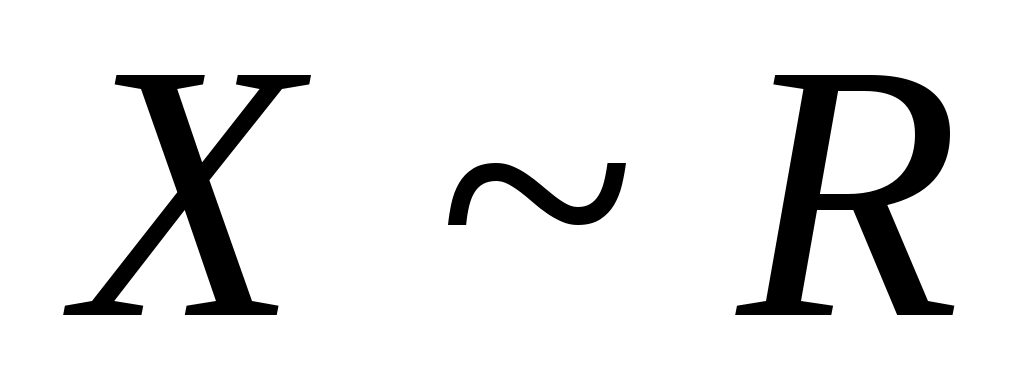 эквиваленттілігі орында – латын болса, онда эквиваленттілігі орында – латын болса, онда 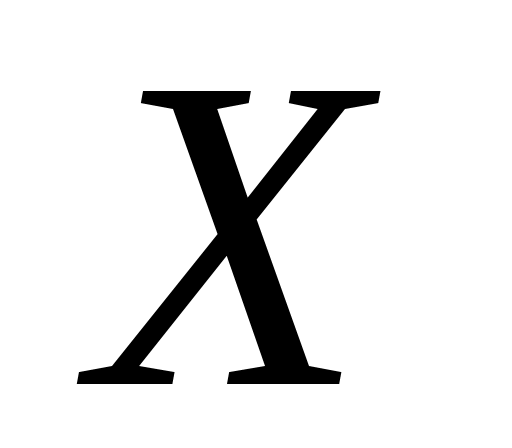 жиынын «континуалды жиын» немесе «қуаты континуум жиын» (қысқаша: «қуаты жиынын «континуалды жиын» немесе «қуаты континуум жиын» (қысқаша: «қуаты 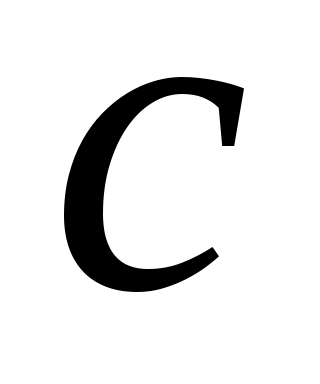 жиын») деп атаймыз. жиын») деп атаймыз.
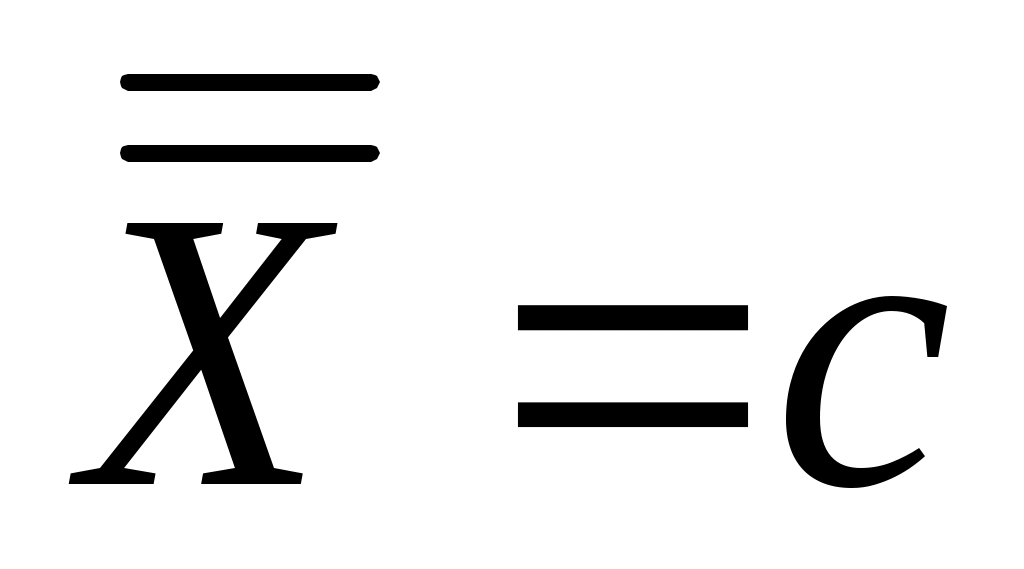 жазуы жазуы 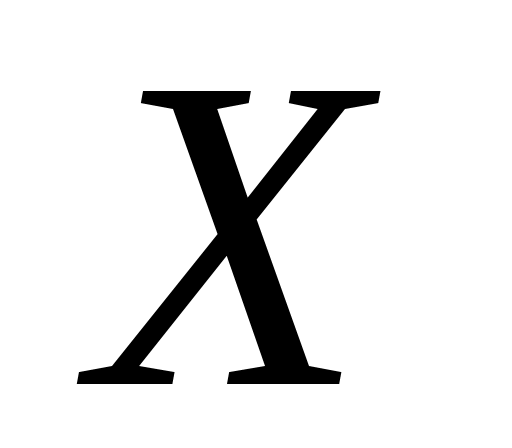 жиынының континуалды жиын екенін білдіреді. Континуалды жиындардың мысалдарын келтірейік. жиынының континуалды жиын екенін білдіреді. Континуалды жиындардың мысалдарын келтірейік.
1– теорема. 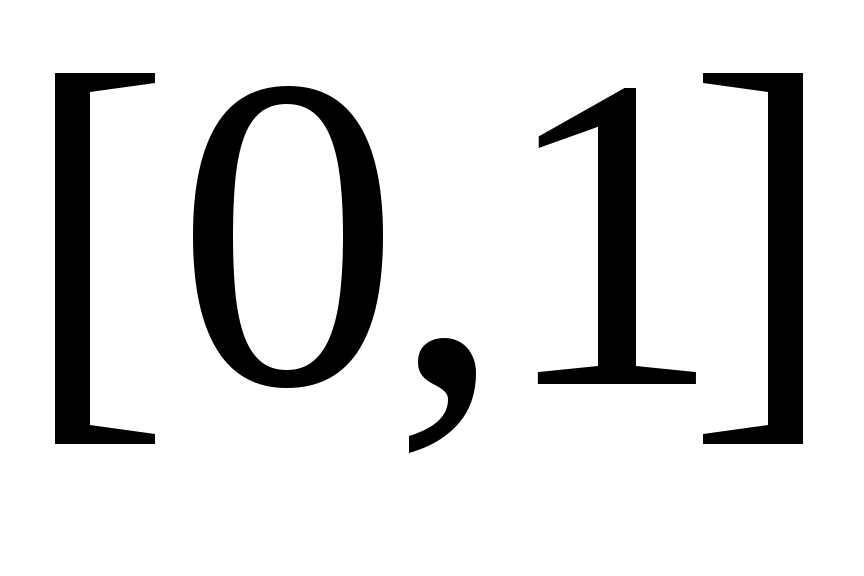 , , 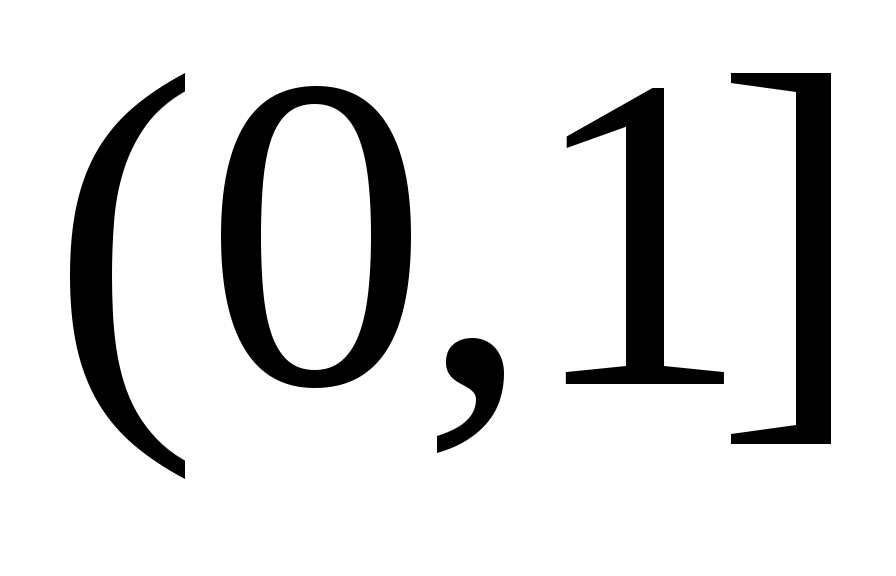 , ,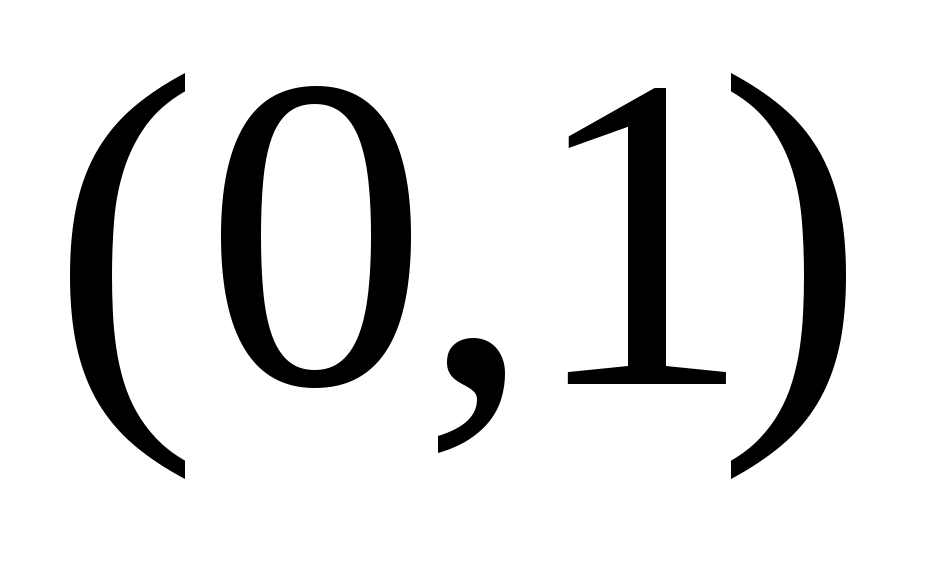 , , 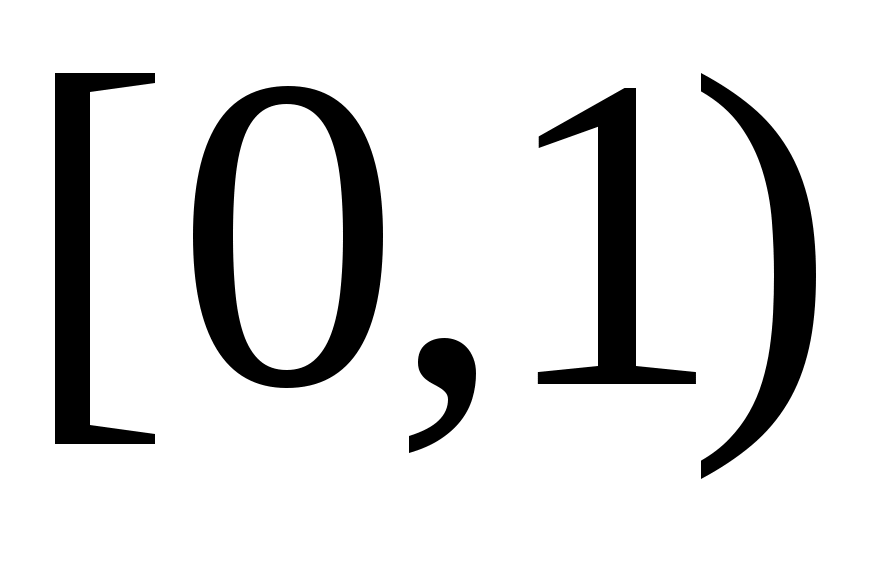 аралықтары – континуалды жиындар. аралықтары – континуалды жиындар.
Дәлелдеуі. 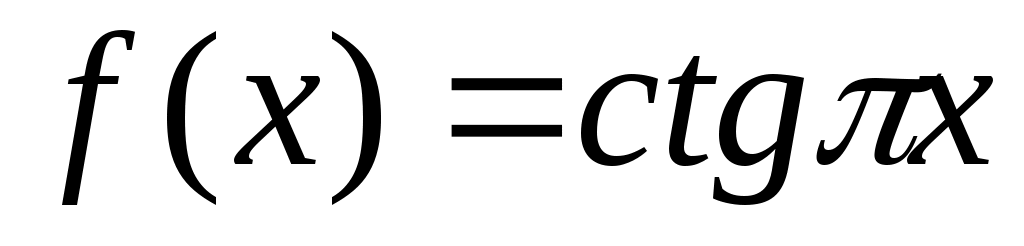 теңдігі бойынша анықталған теңдігі бойынша анықталған 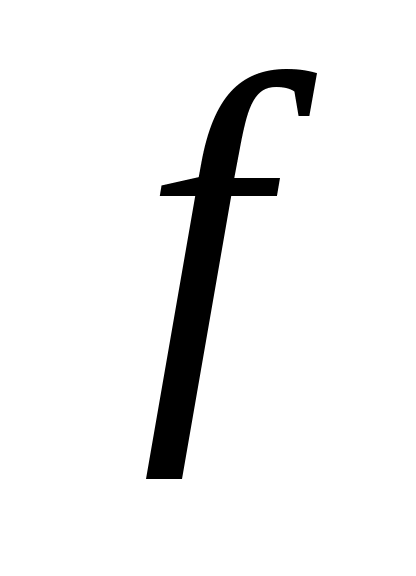 функциясы функциясы 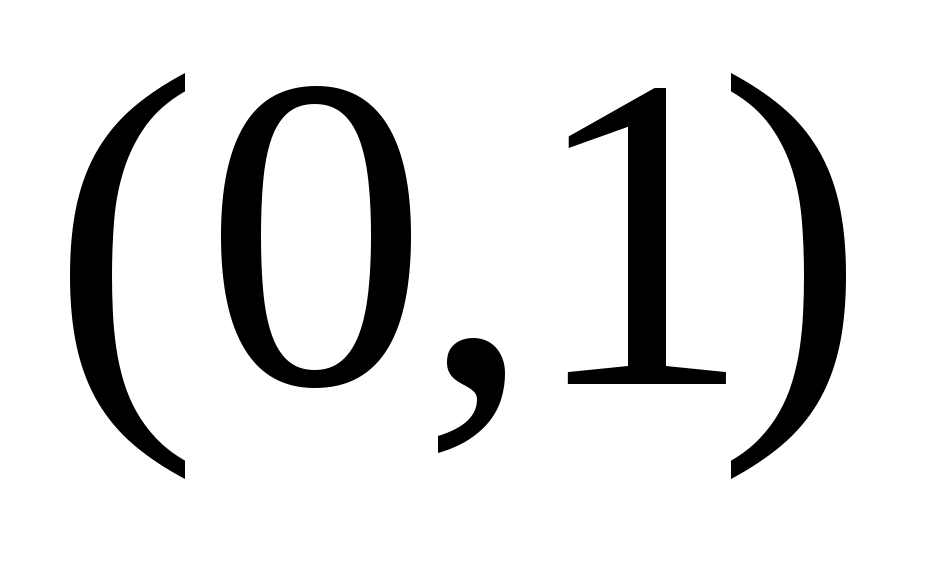 және және 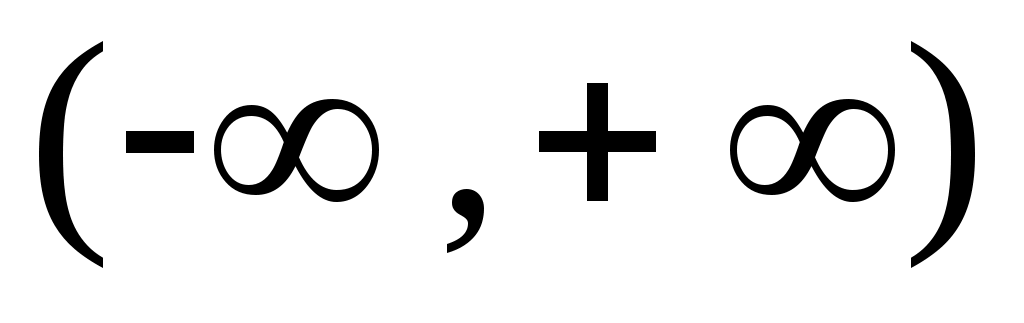 аралықтары арасында өзара бірмәнді сәйкестік орнатады. Демек, аралықтары арасында өзара бірмәнді сәйкестік орнатады. Демек, 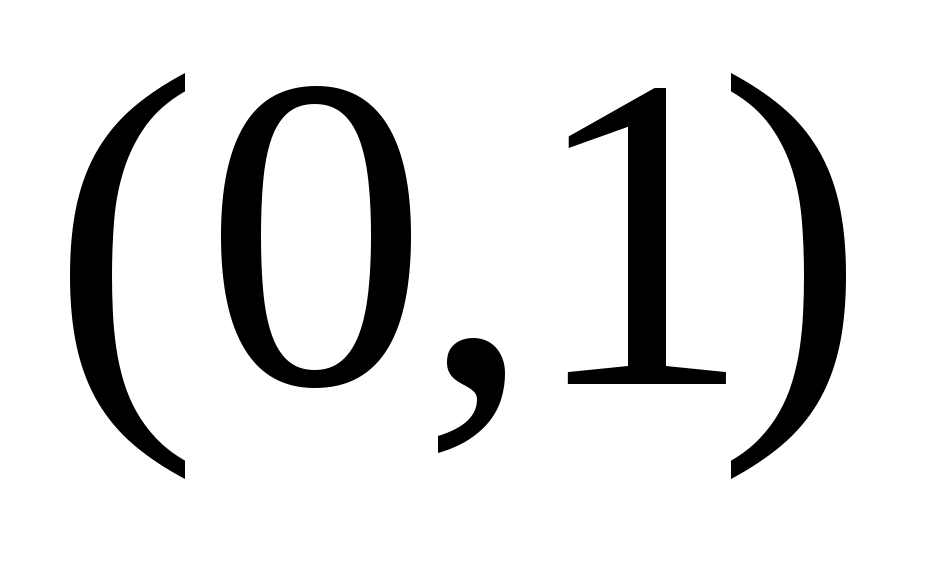 жиыны – континуалды жиын. Ал қалған аралықтар үшін жиыны – континуалды жиын. Ал қалған аралықтар үшін
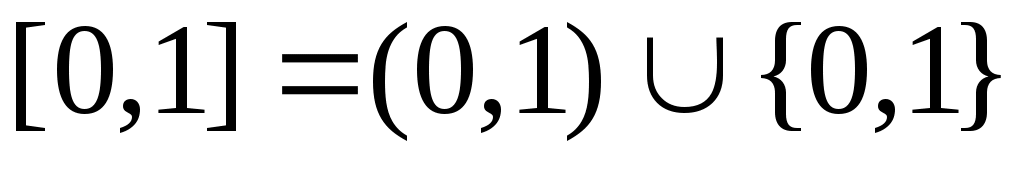 , , 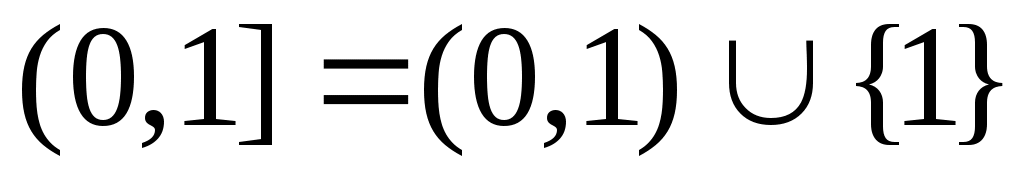 , , 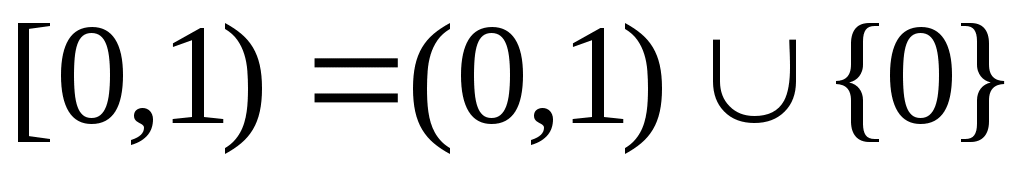
теңдіктері орындалады. Ендеше, 8 – теорема (§3) бойынша 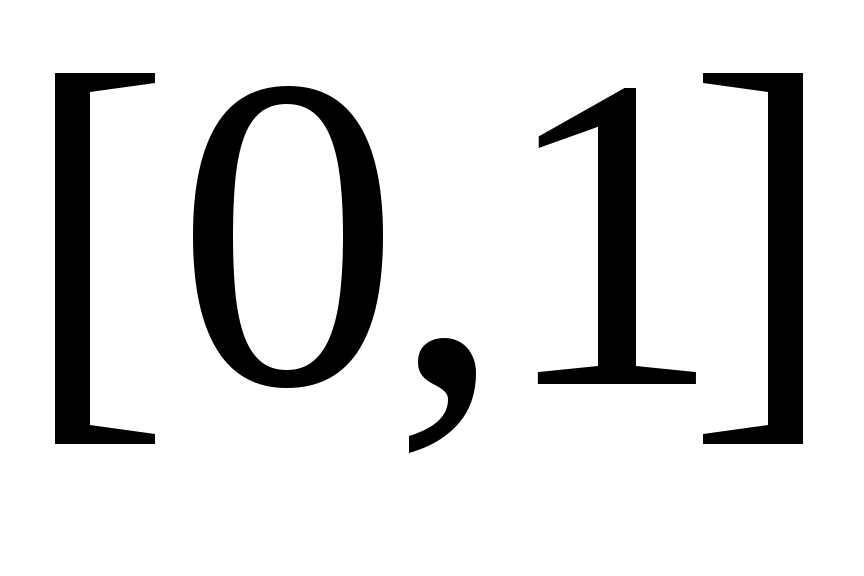 , , 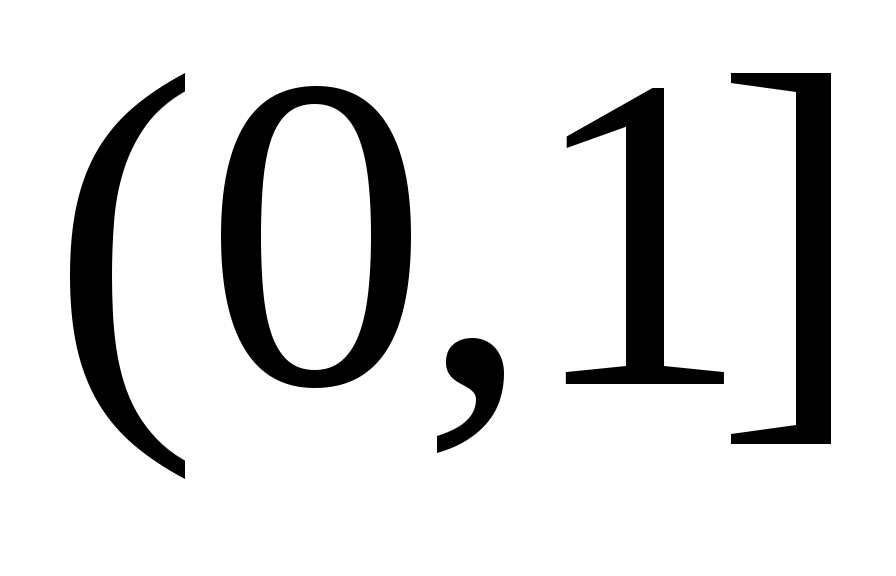 , , 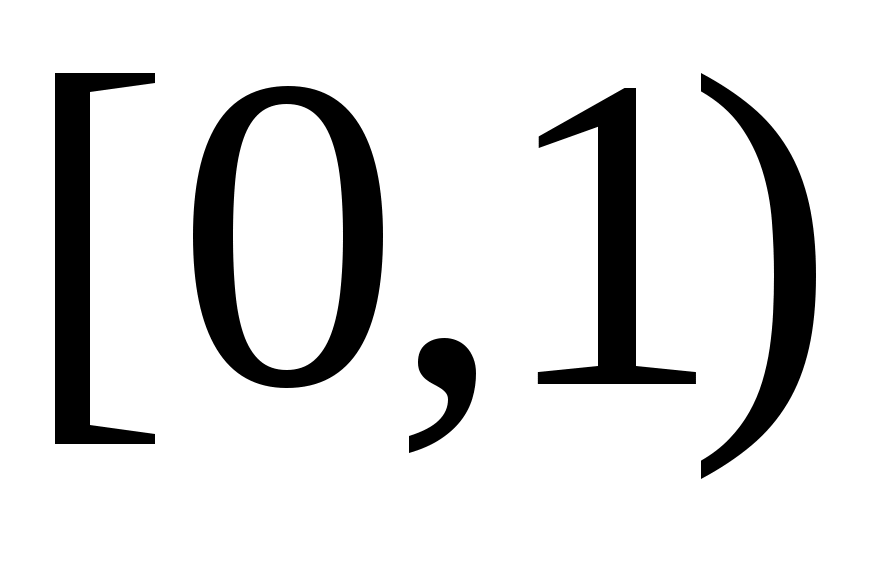 аралықтары – континуалды жиындар. аралықтары – континуалды жиындар.
2 – теорема. 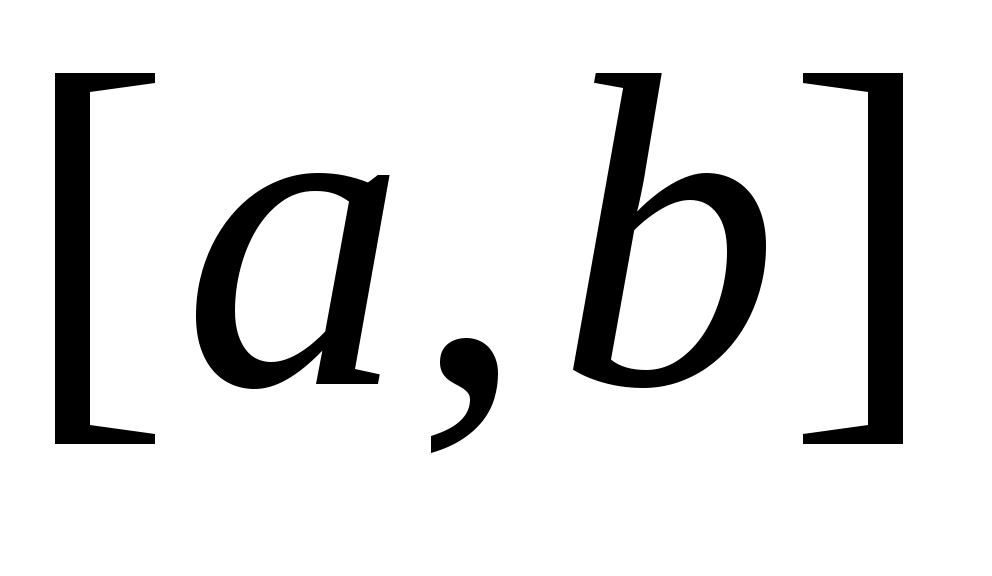 , , 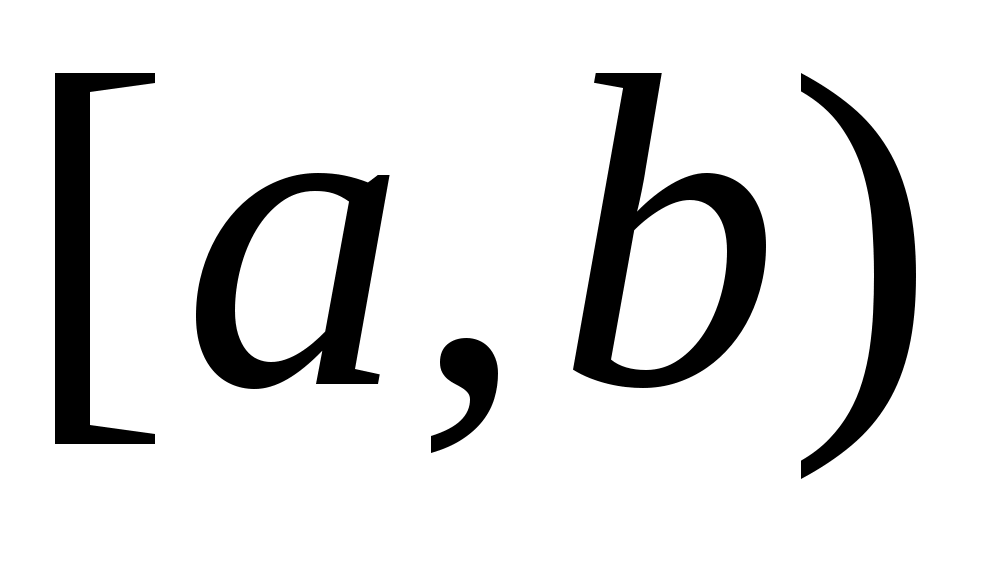 , ,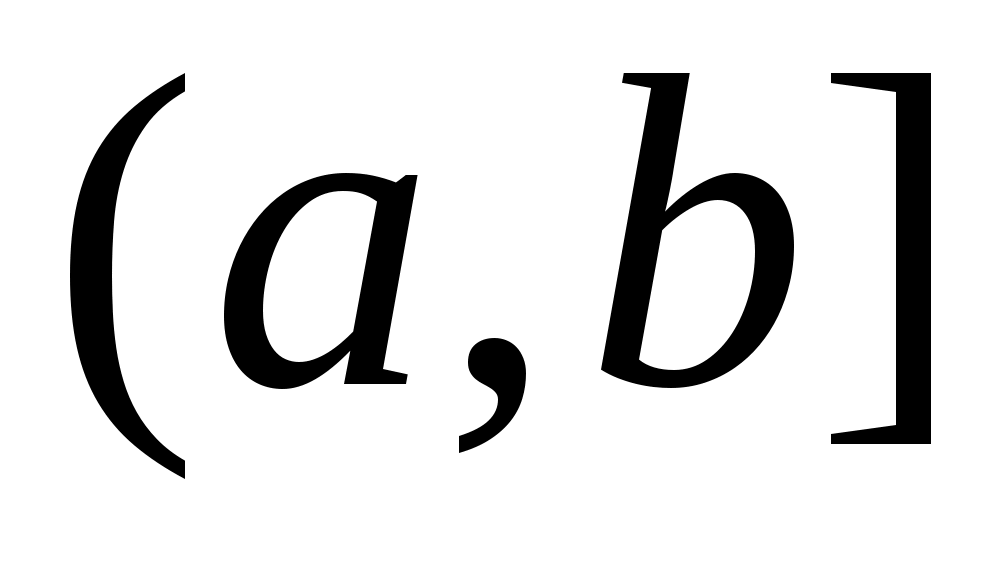 , , 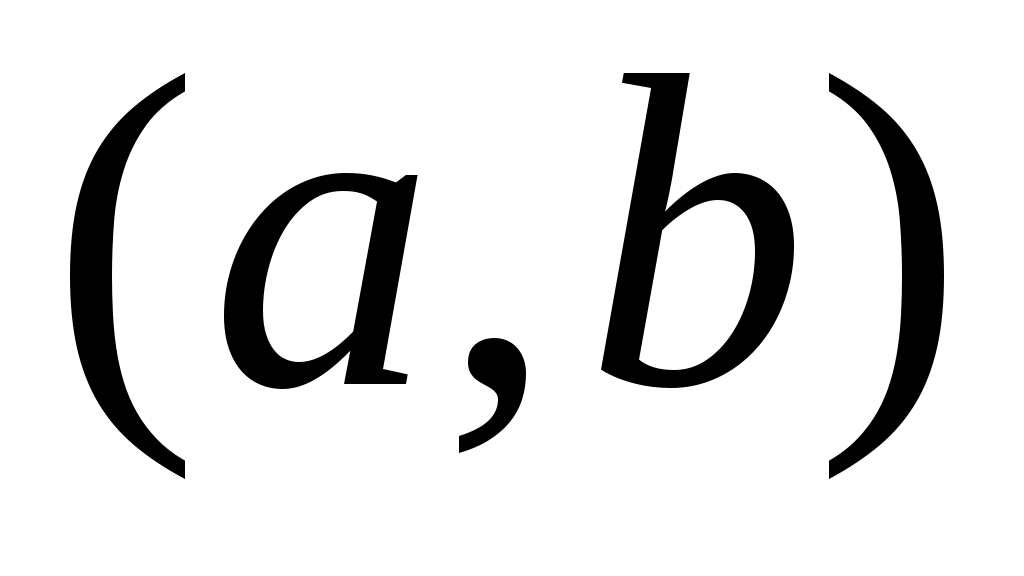 , , 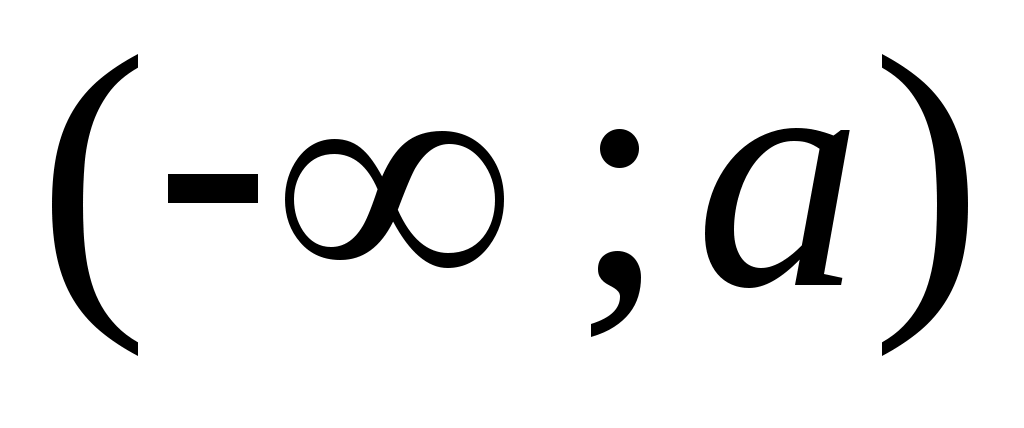 , , 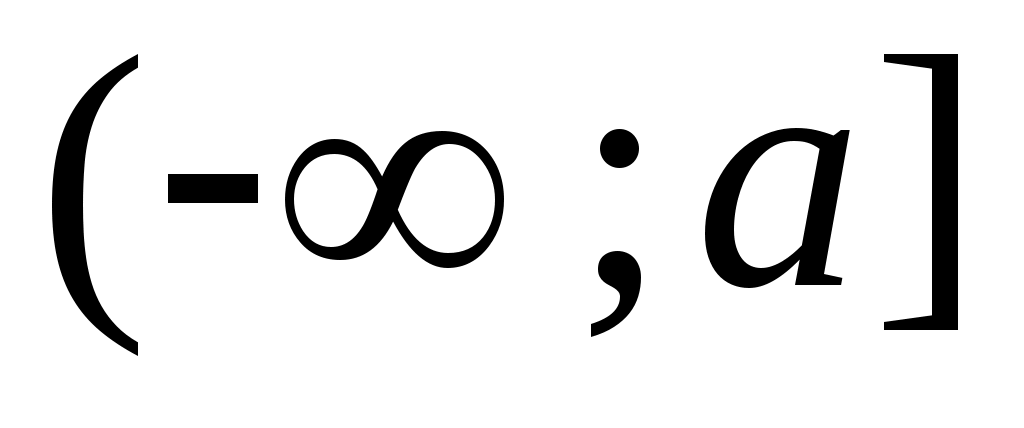 , , 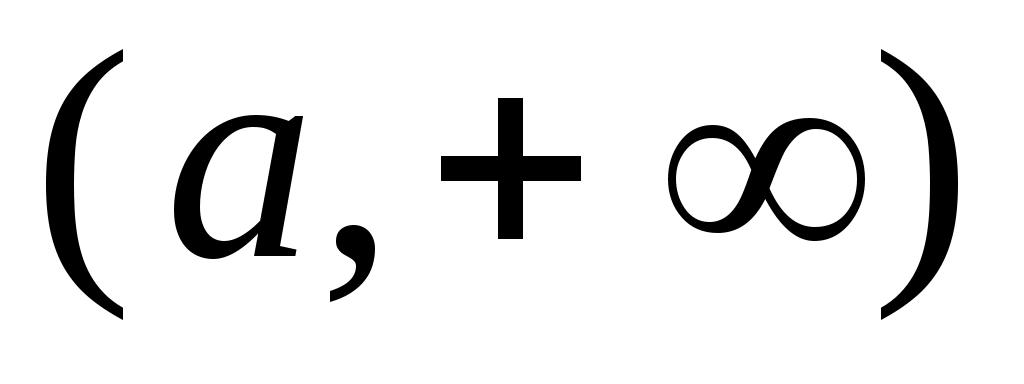 , , 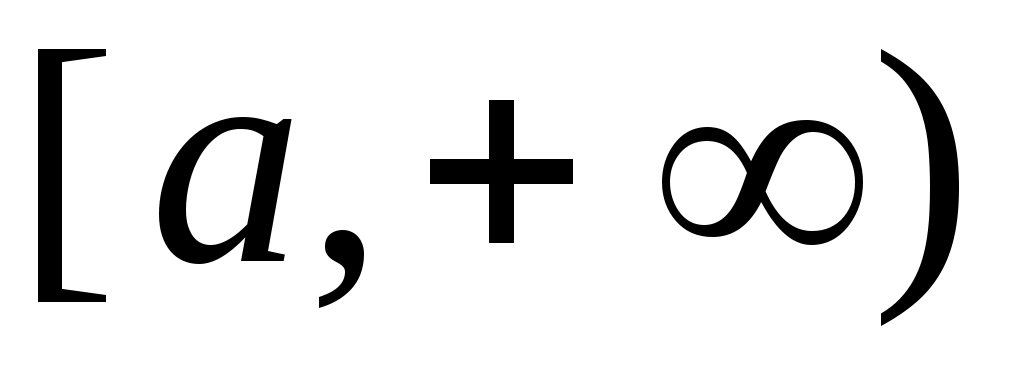 аралықтары – континуалды жиындар. аралықтары – континуалды жиындар.
Дәлелдеуі. 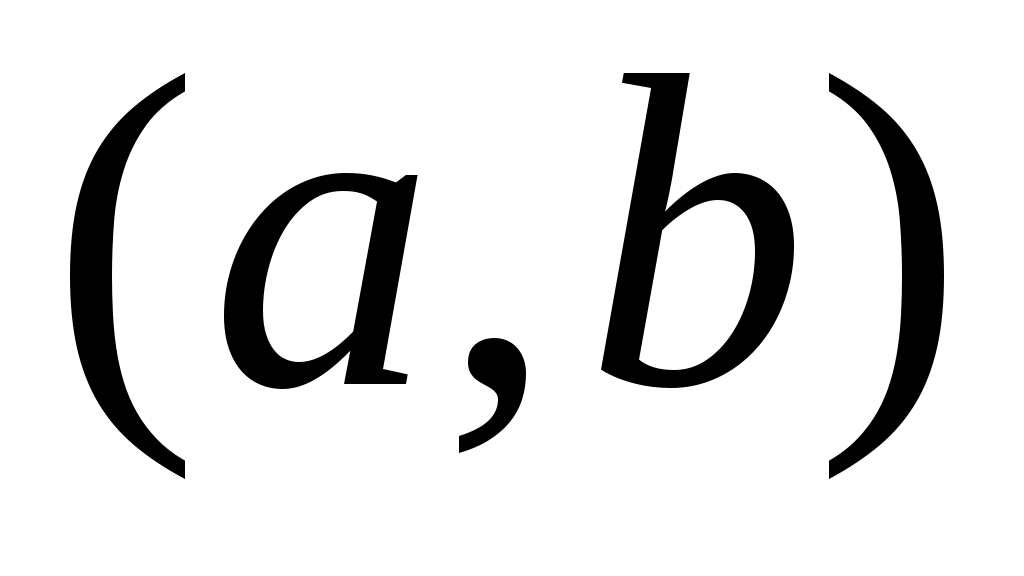 , , 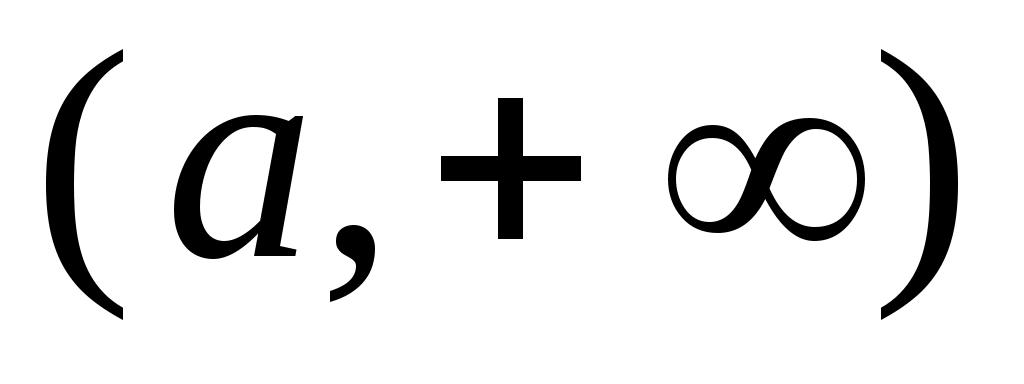 , , 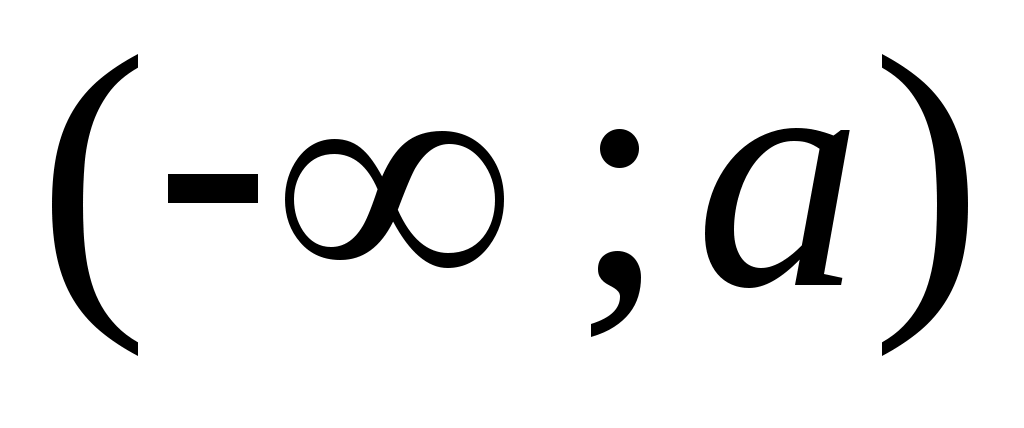 аралықтарының континуалды жиындар екенін көрсетсек жеткілікті, өйткені, қалған аралықтар осы аралықтарға бір немесе екі нүктені қосқаннан алынады. аралықтарының континуалды жиындар екенін көрсетсек жеткілікті, өйткені, қалған аралықтар осы аралықтарға бір немесе екі нүктені қосқаннан алынады.
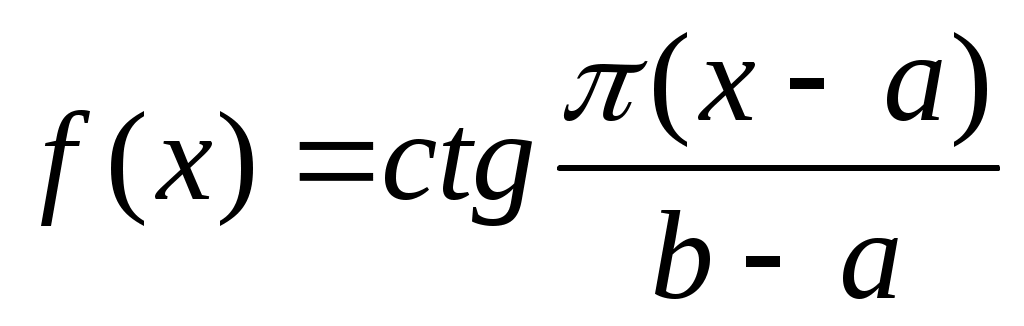 ( (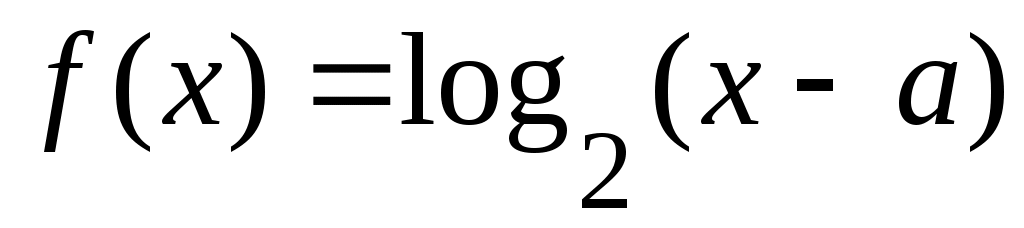 , , 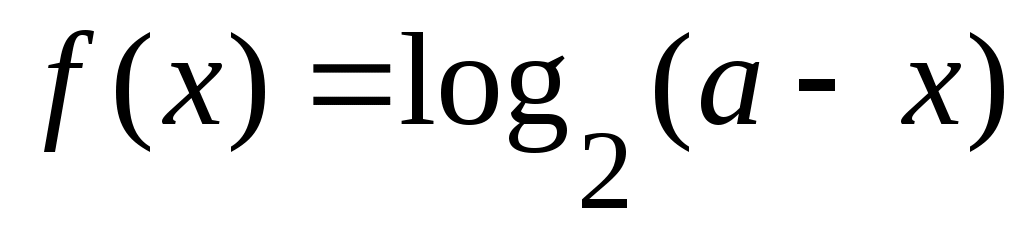 ) )
теңдігі бойынша анықталған 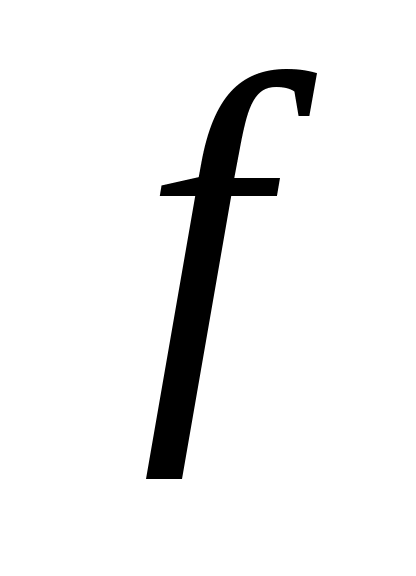 функциясы функциясы 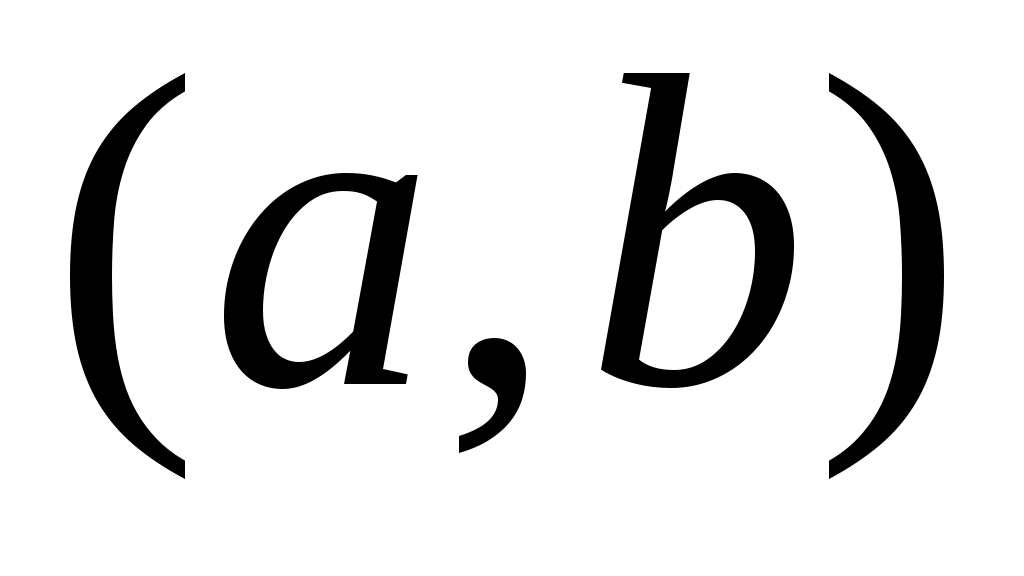 ( (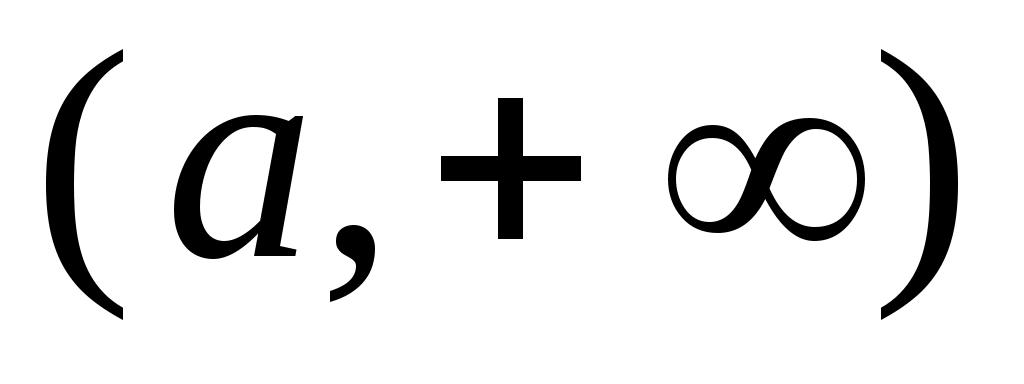 , , 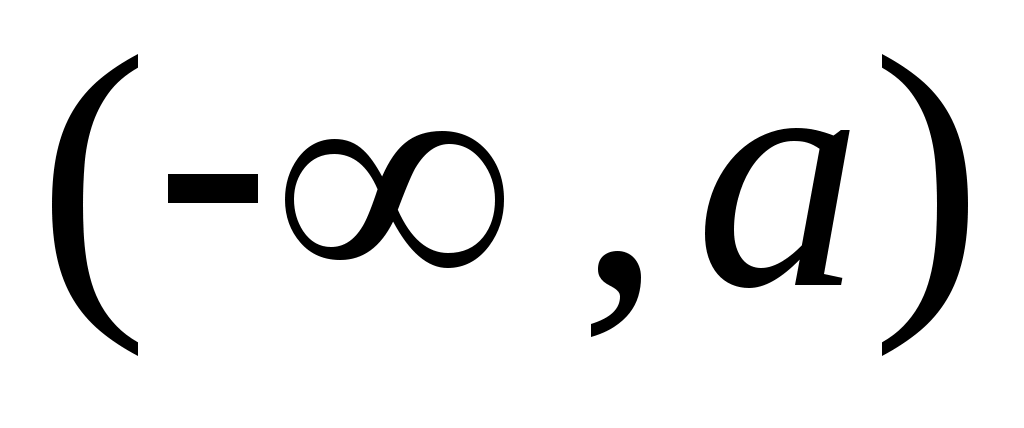 ) )
және 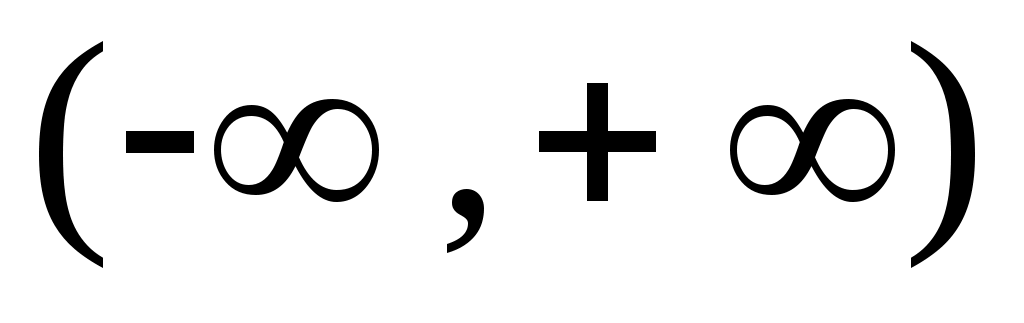 аралықтары арасында өзара бірмәнді сәйкестік орнатады. аралықтары арасында өзара бірмәнді сәйкестік орнатады.
3 – теорема. Әрбір мүшесі натурал сандар жиынында жататын тізбек – тер жиыны – континуалды жиын.
Дәлелдеуі. Әрбір мүшесі натурал сандар жиынында жататынтізбектер жиынын 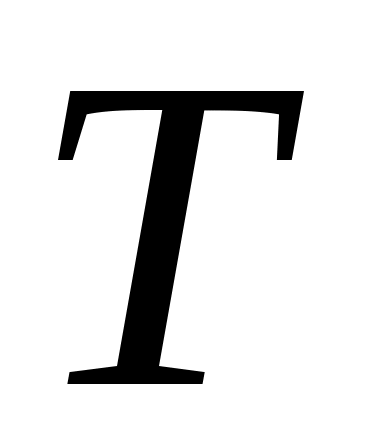 арқылы таңбалайық, яғни, арқылы таңбалайық, яғни, 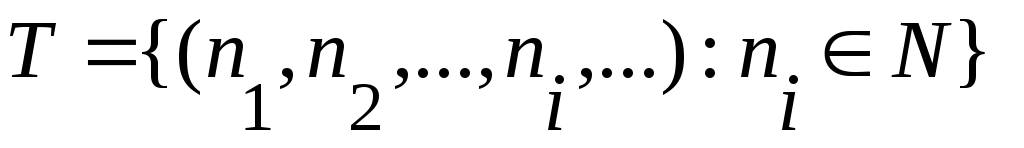 . .
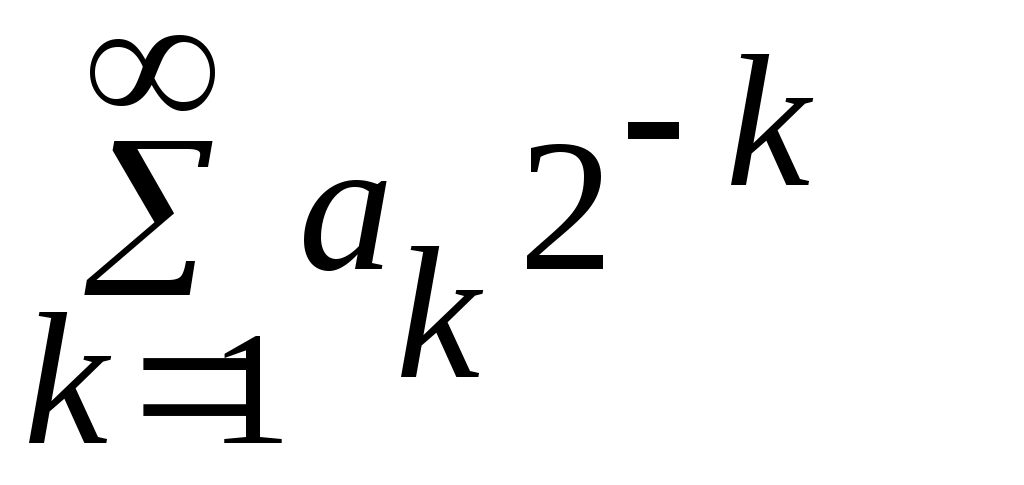 ( (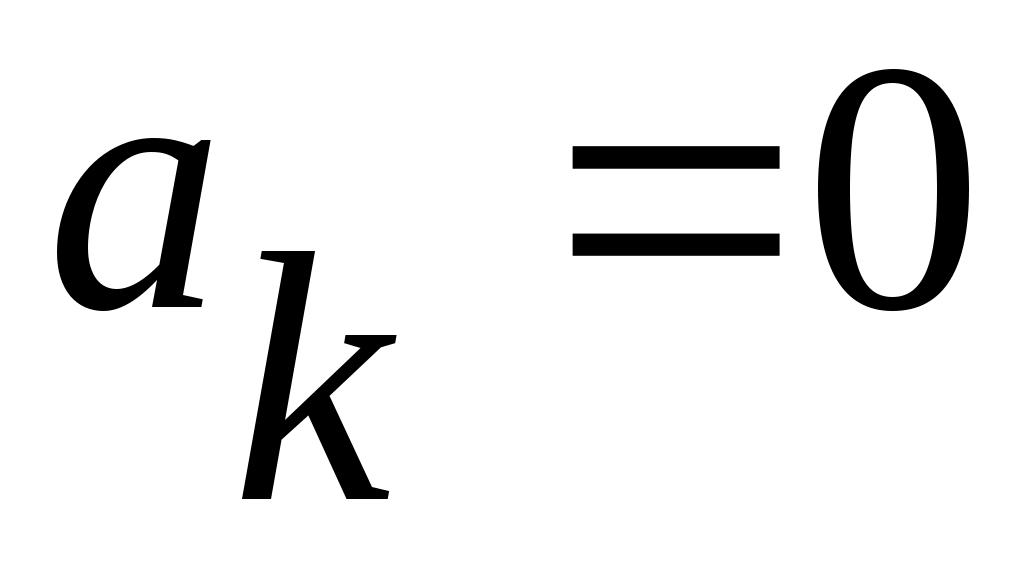 немесе немесе 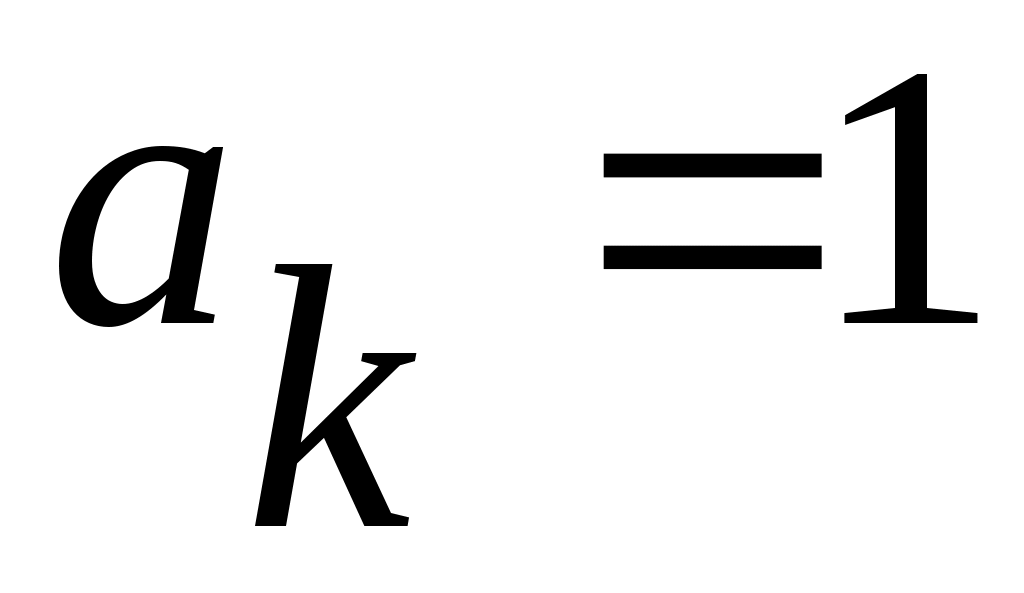 ) қатарының қосындысы екілікбөлшек деп аталып, ) қатарының қосындысы екілікбөлшек деп аталып, 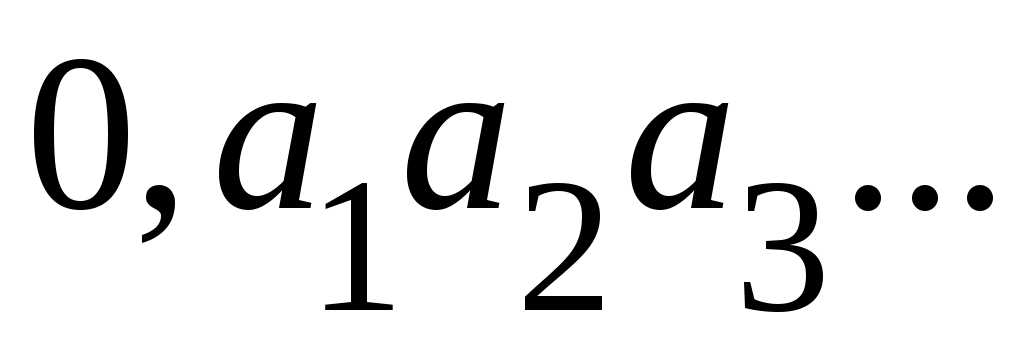 символымен белгіленеді. символымен белгіленеді. 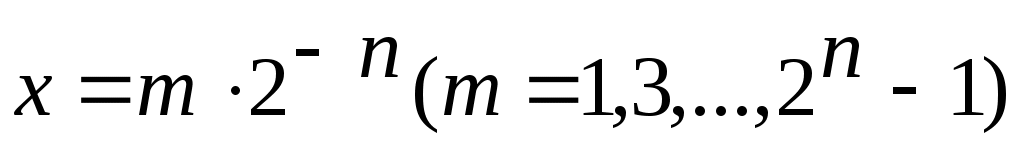 нүктесін нүктесін
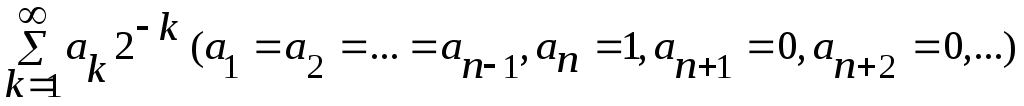 немесе немесе
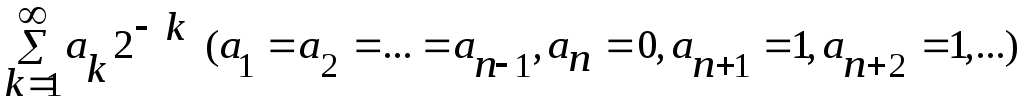 (1) (1)
қатарларының қосындысы түрінде жазуға болады. Мәселен, 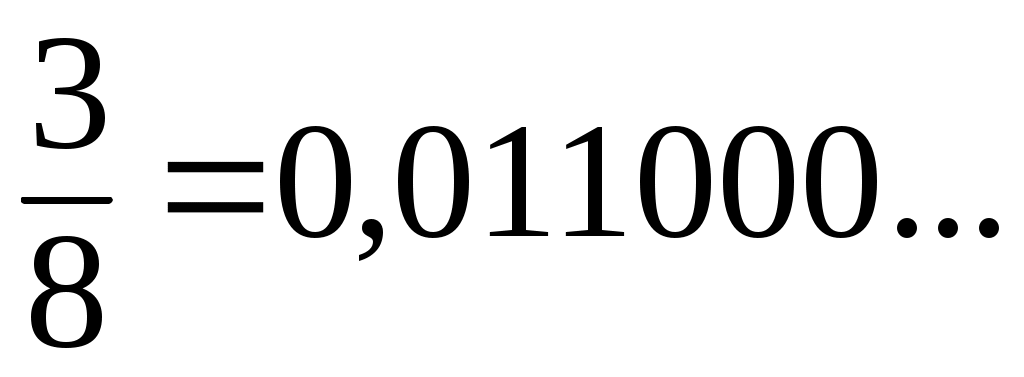 немесе немесе 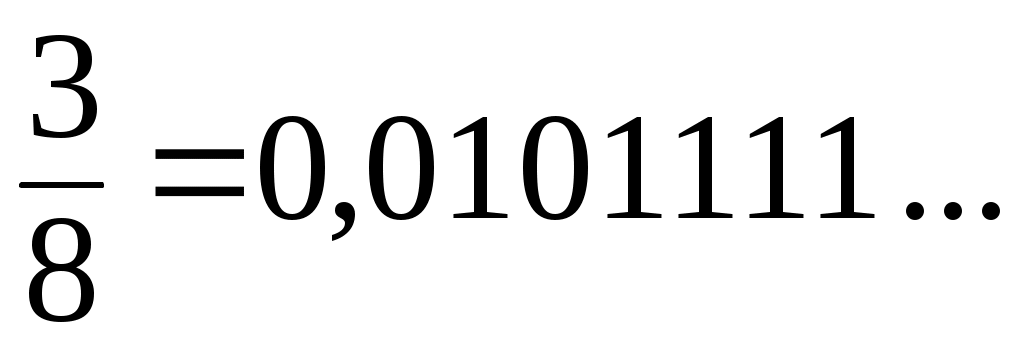 . Егер (1) түріндегі қатарларды қолданбайтын болсақ, онда . Егер (1) түріндегі қатарларды қолданбайтын болсақ, онда
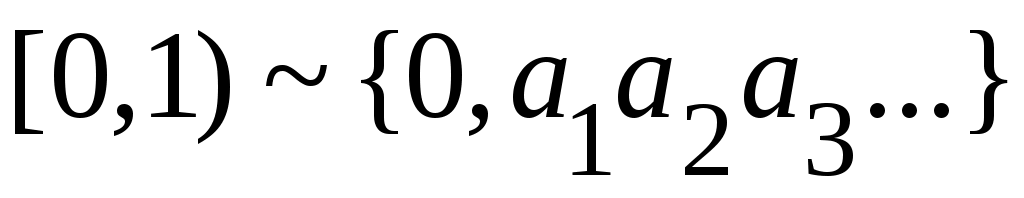 (2) (2)
эквиваленттілігін аламыз.
Әрбір 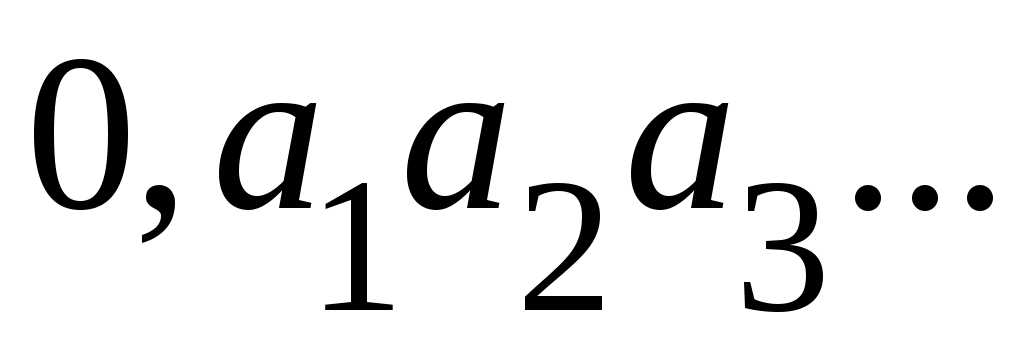 қосындысы қосындысы 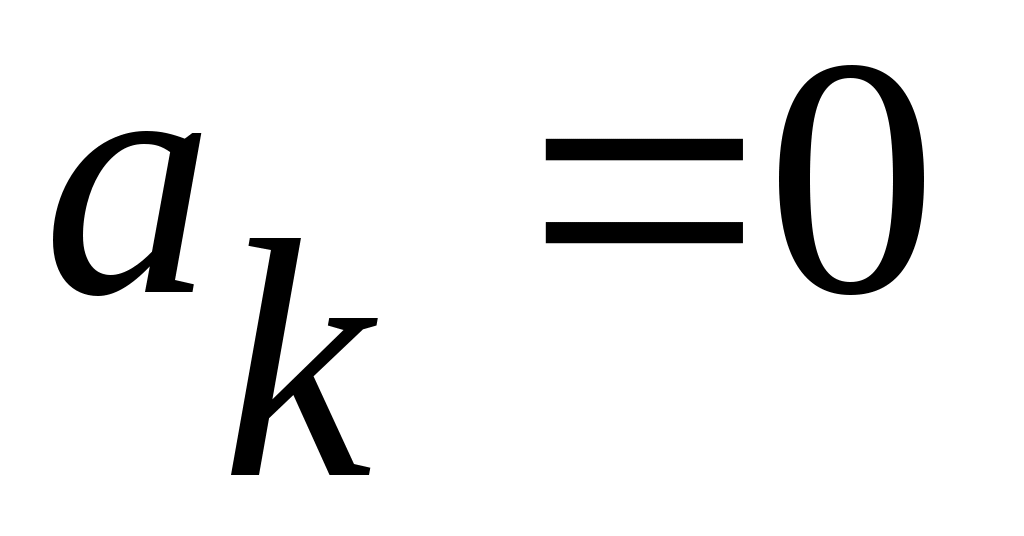 теңдігін қанағаттандыратын теңдігін қанағаттандыратын 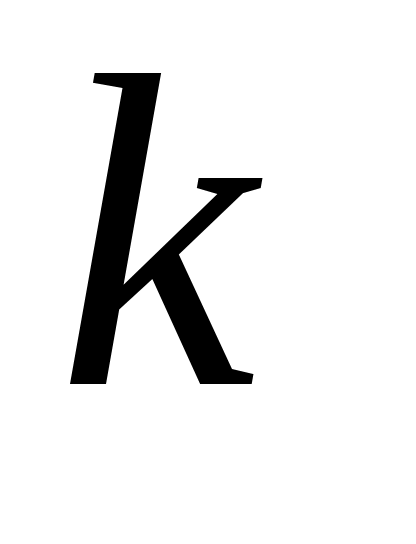 индекстерінің өспелі индекстерінің өспелі 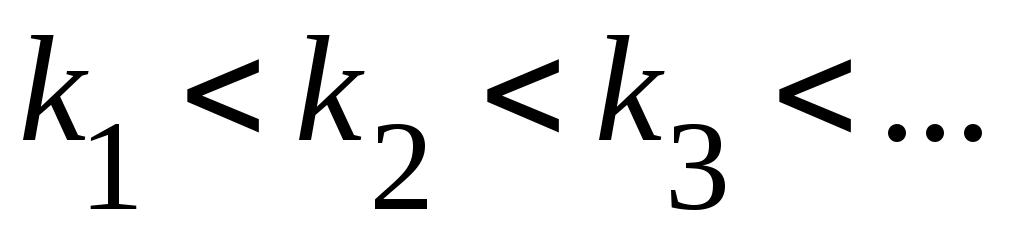 тізбегі бойынша бірмәнді анықталады, яғни, тізбегі бойынша бірмәнді анықталады, яғни,
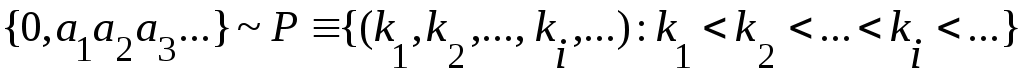 . (3) . (3)
Ал 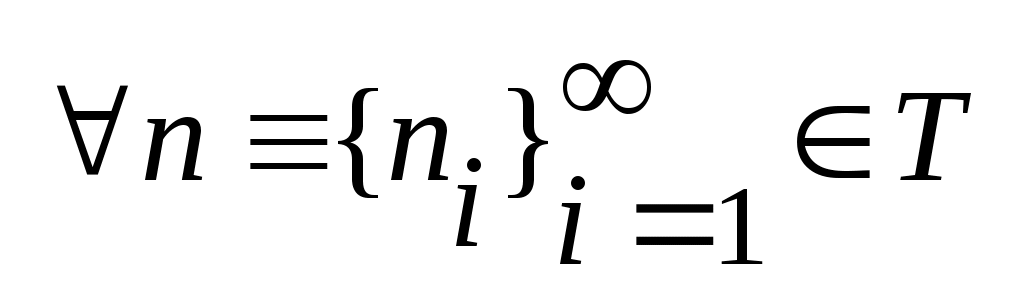 нүктесінде нүктесінде 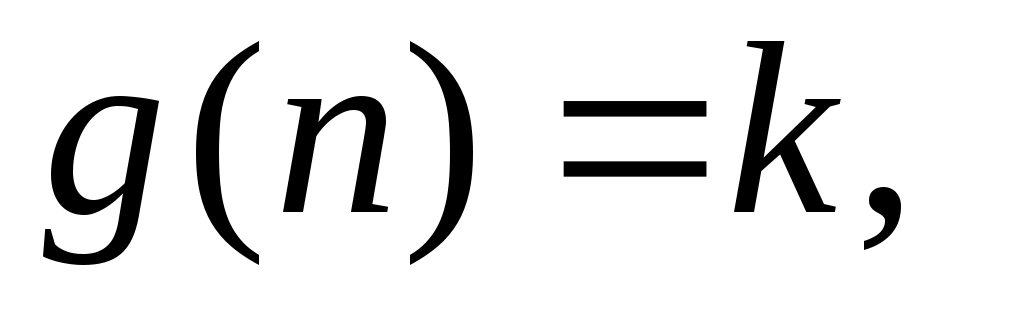 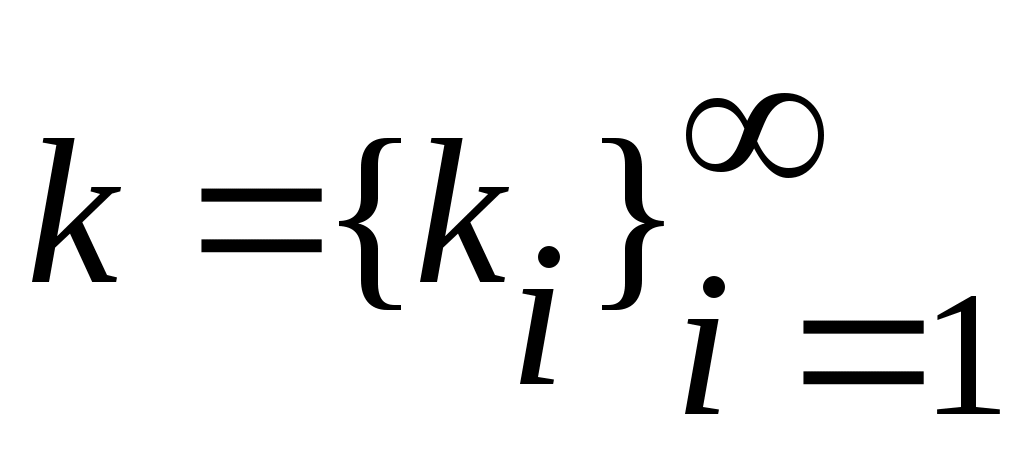 , , 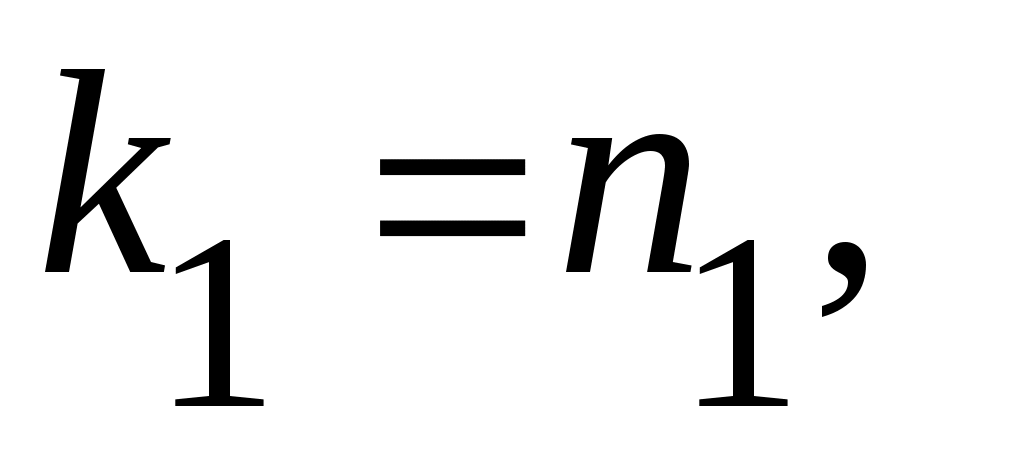 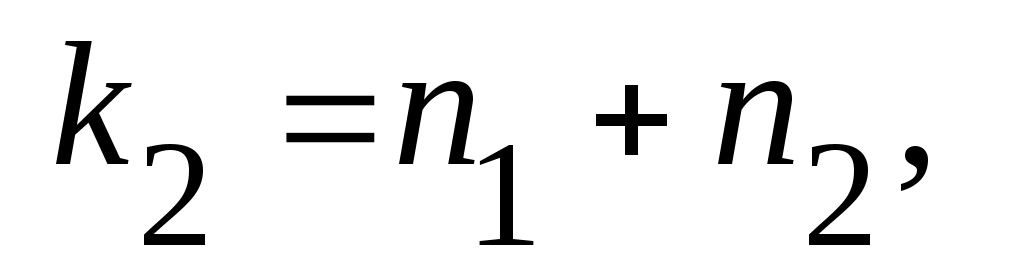
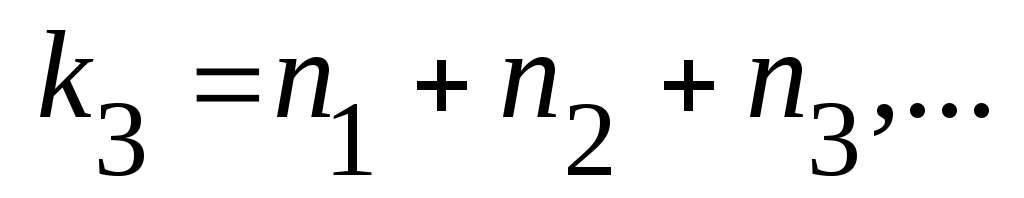 теңдігін қанағаттандыратын теңдігін қанағаттандыратын 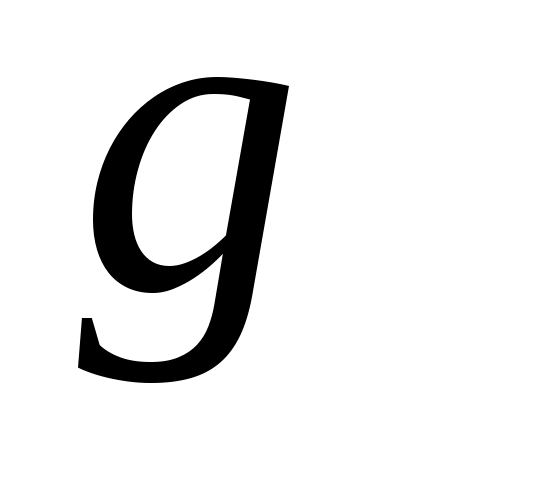 функциясы функциясы 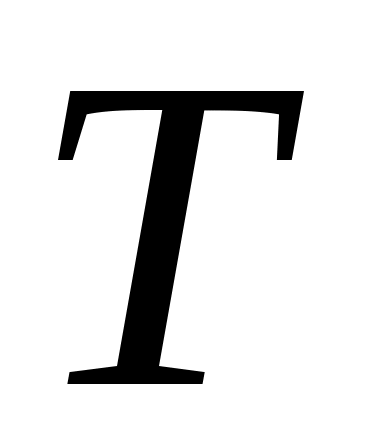 және және 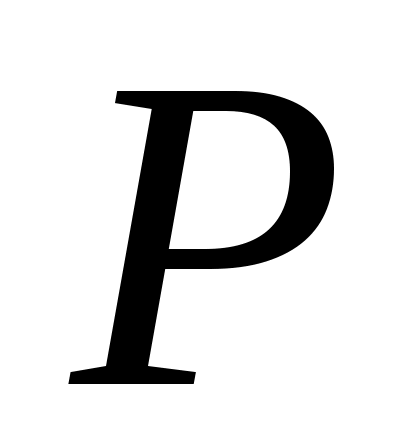 жиындары арасында өзара бірмәнді сәйкестік орнатады. Демек, жиындары арасында өзара бірмәнді сәйкестік орнатады. Демек, 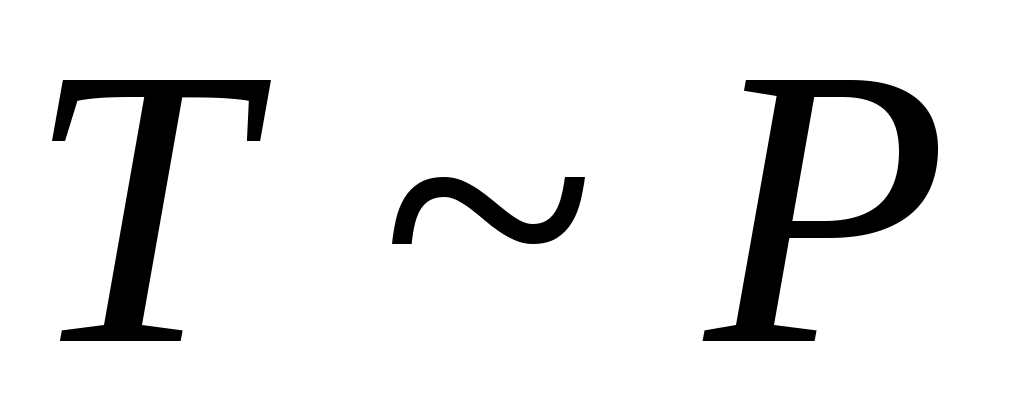 . .
(2), (3) және 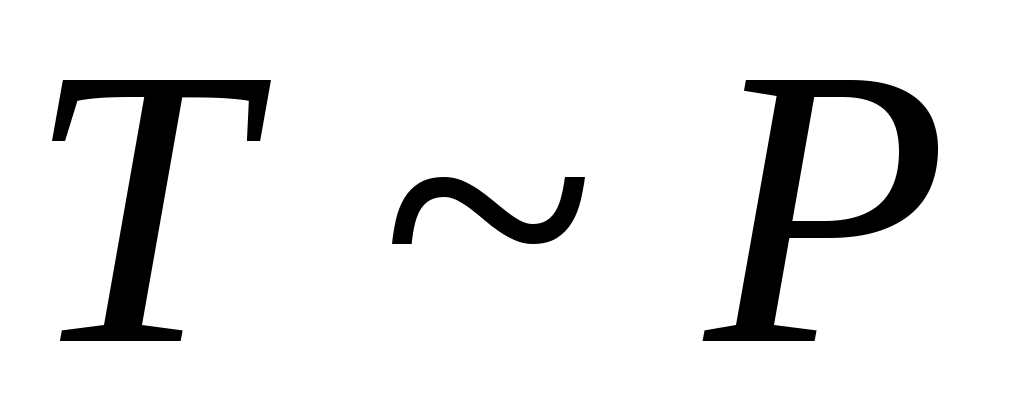 эквиваленттіліктерінен 1 – теорема (§2) бойынша эквиваленттіліктерінен 1 – теорема (§2) бойынша 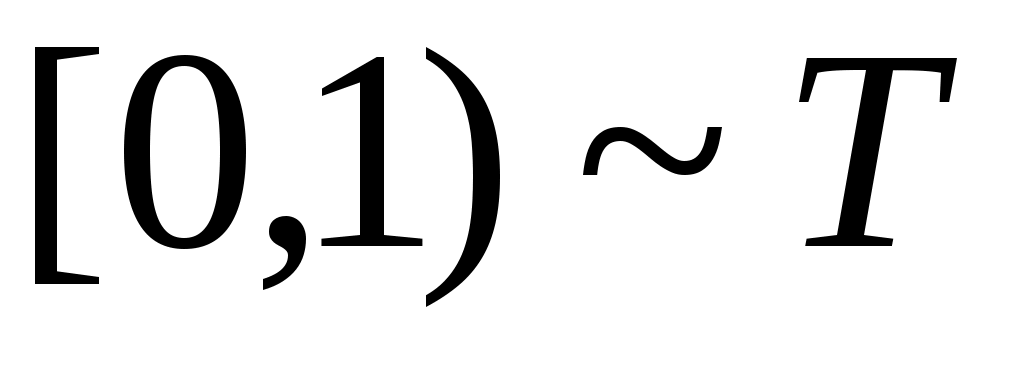 эквиваленттілігі шығады. эквиваленттілігі шығады.
4 – теорема. 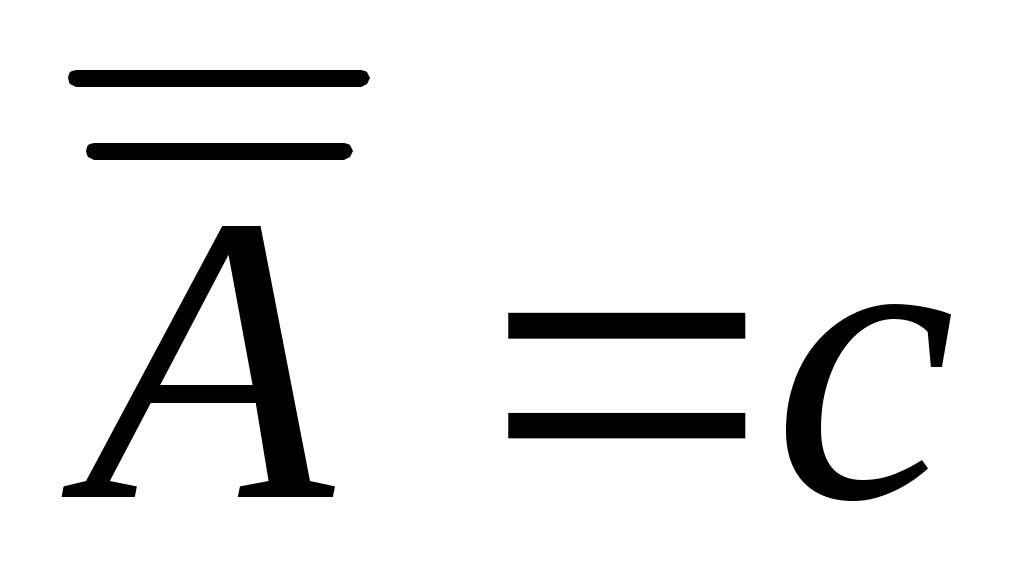 , ,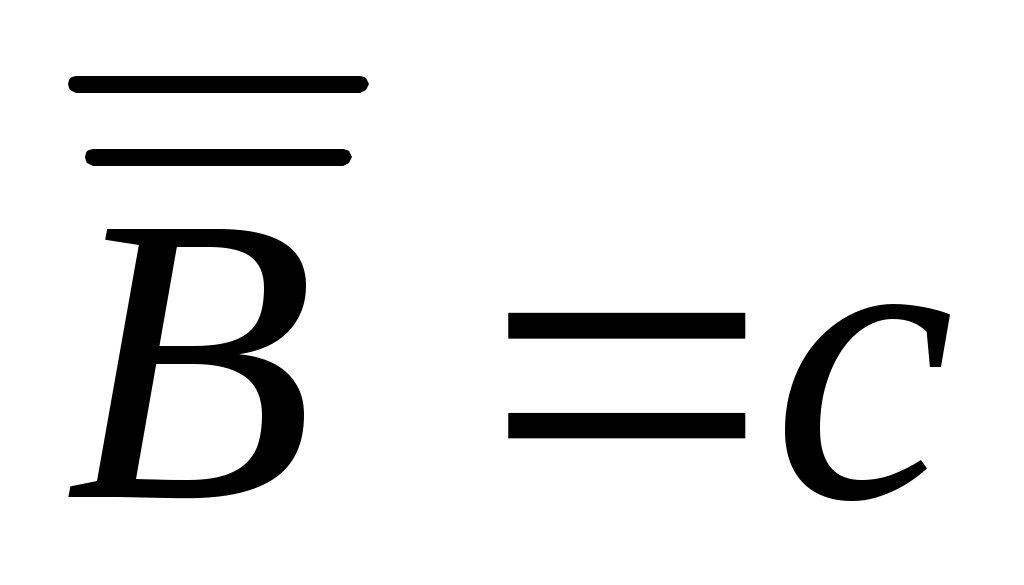 жиындары үшін жиындары үшін  жиыны – континуалды жиын. жиыны – континуалды жиын.
Дәлелдеуі. Алдыңғы теорема бойынша 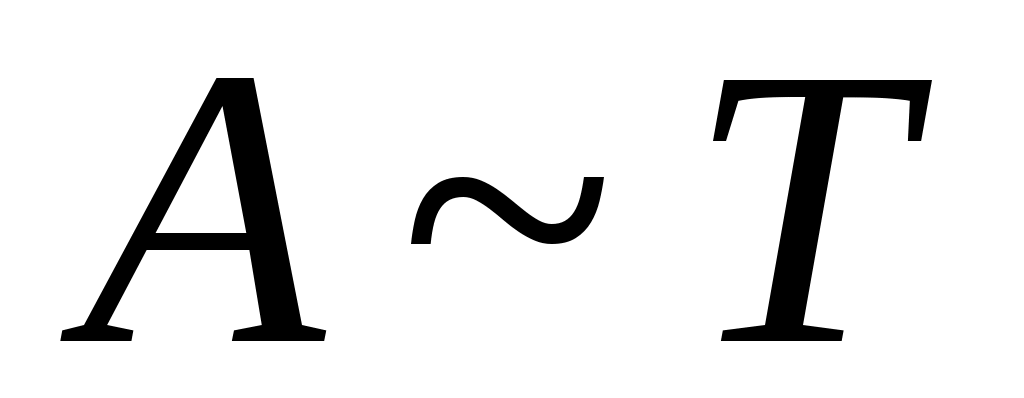 және және 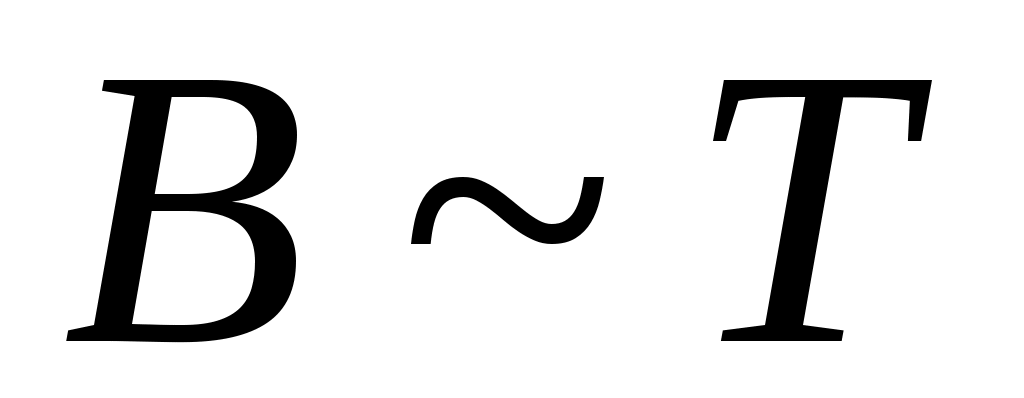 . Егер . Егер
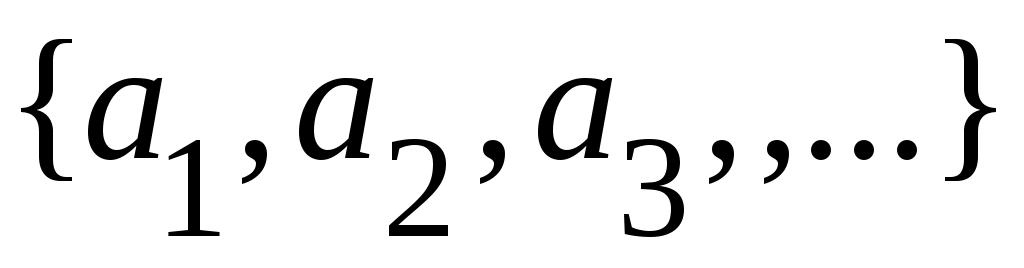 және және 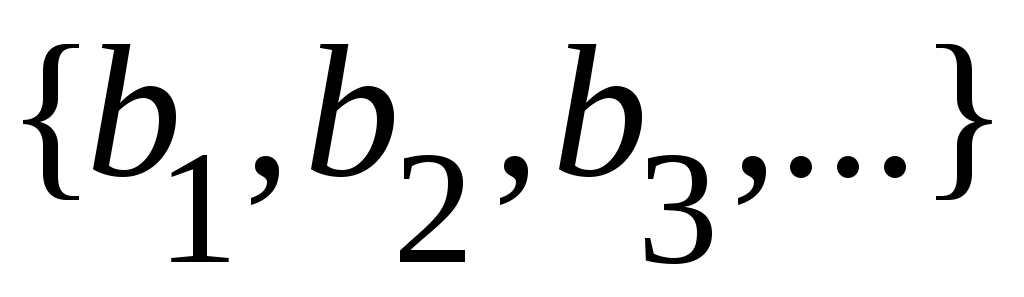 тізбектері тізбектері  және және 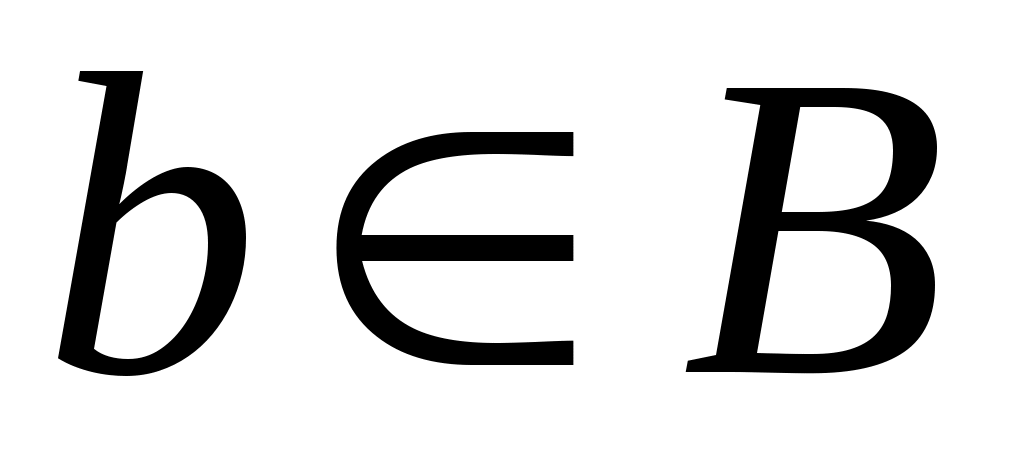 элементтеріне сәйкес тізбектер болса, онда әрбір элементтеріне сәйкес тізбектер болса, онда әрбір  элементіне элементіне
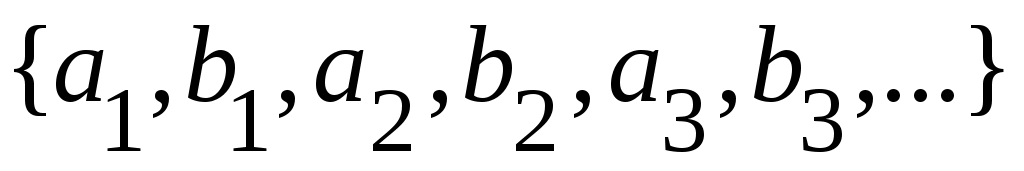 тізбегін сәйкес қоятын тізбегін сәйкес қоятын  функциясы функциясы  және және 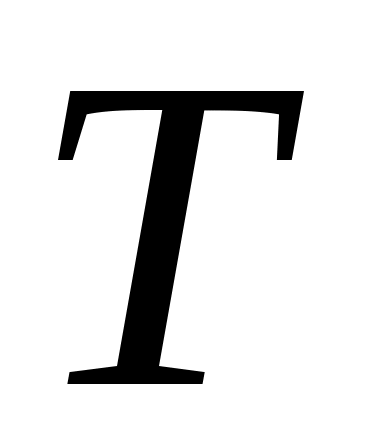 жиындары арасында өзара бірмәнді сәйкестік орнатады. Ендеше, жиындары арасында өзара бірмәнді сәйкестік орнатады. Ендеше, 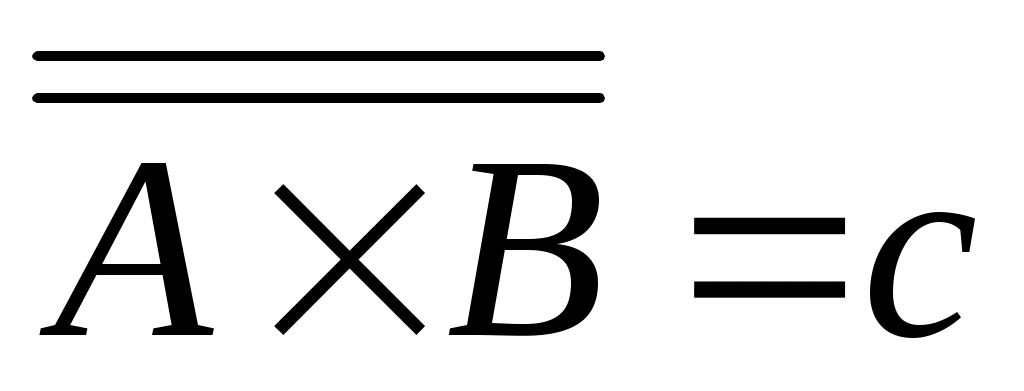 . .
5 – теорема. Өзара қиылыспайтын континуалды жиындардың ақырлы бірігуі – континуалды жиын.
Дәлелдеуі. 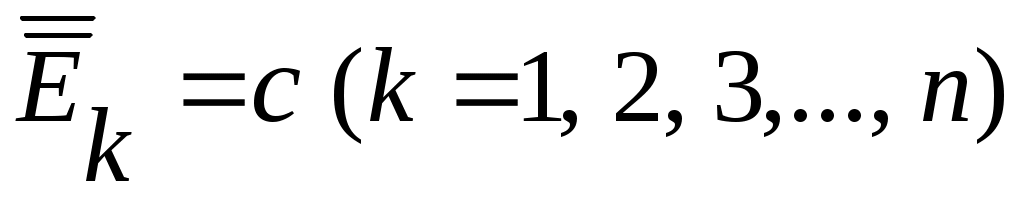 және және 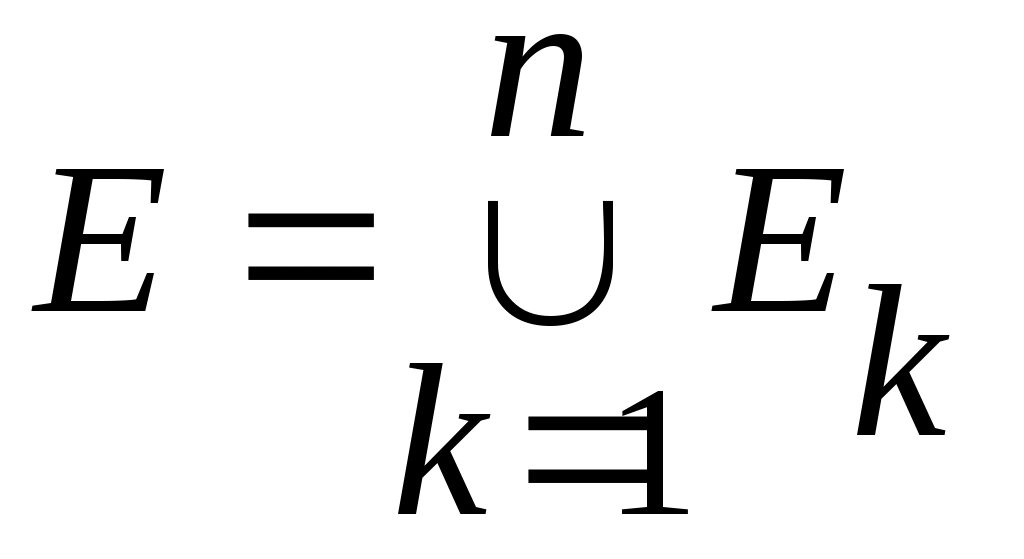 болсын. болсын. 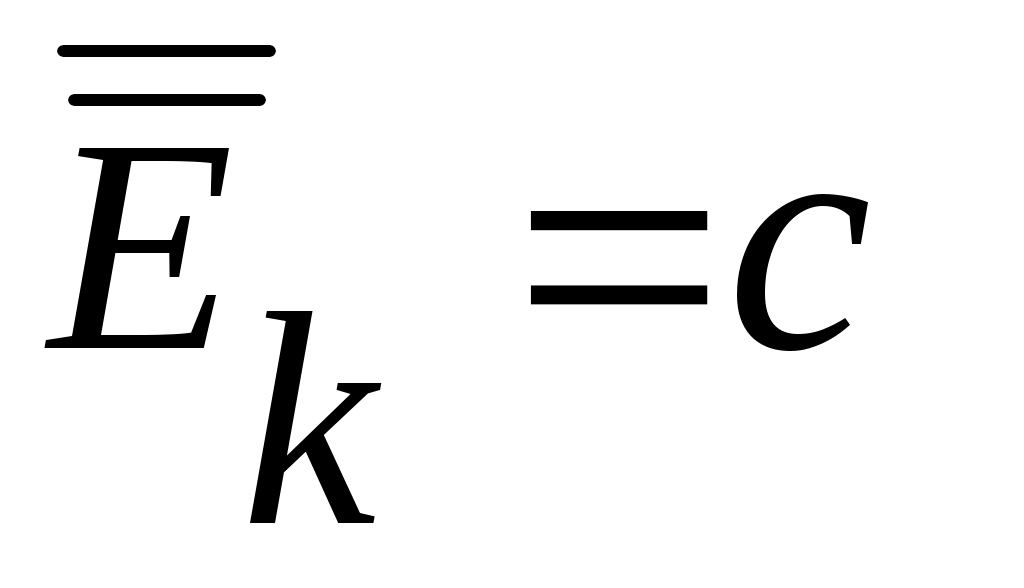 теңдігі бойынша әрбір теңдігі бойынша әрбір 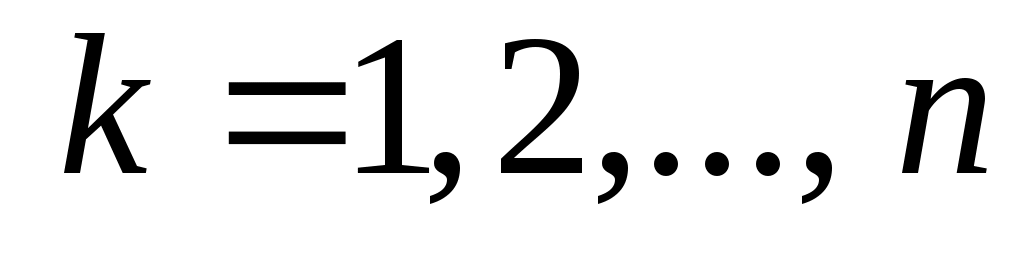 үшін үшін 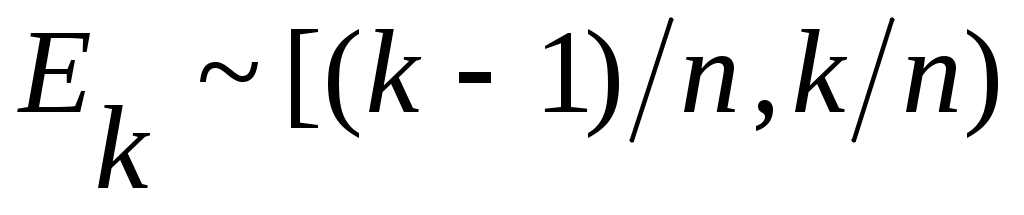 . Енді . Енді 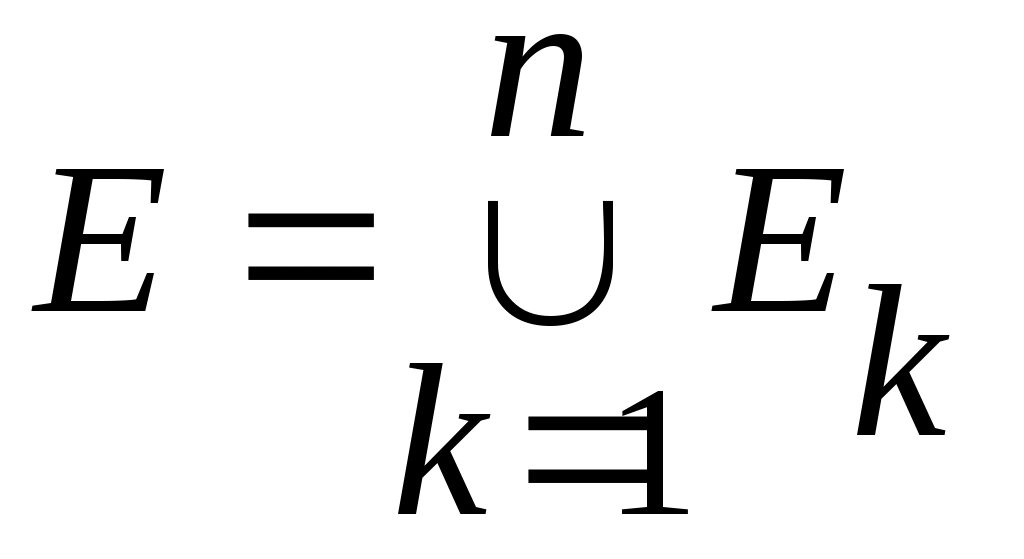 және және 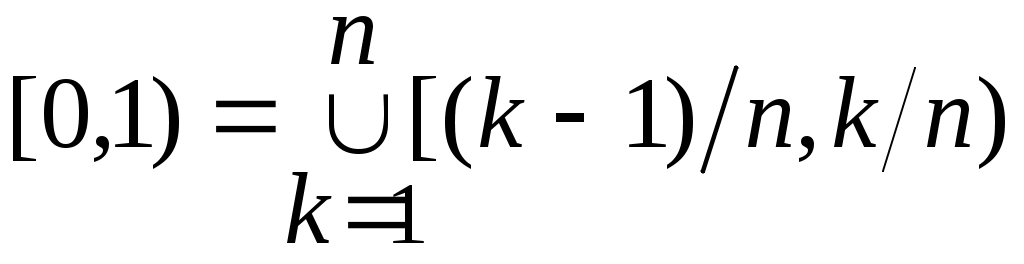 теңдіктерін ескеріп, 2 – теореманы (§2) қолдансақ теңдіктерін ескеріп, 2 – теореманы (§2) қолдансақ
болғаны.
6 – теорема. Өзара қиылыспайтын континуалды жиындардың саналымды бірігуі – континуалды жиын.
Дәлелдеуі. 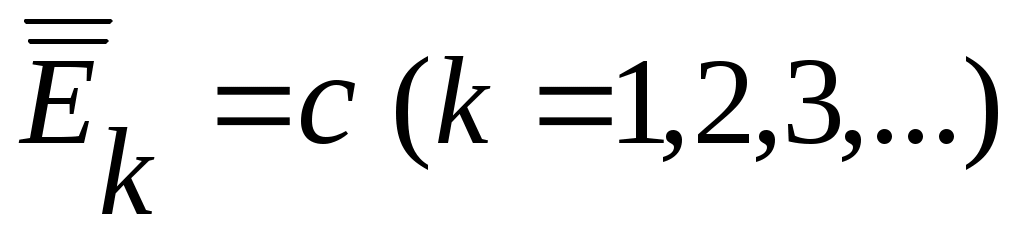 және және 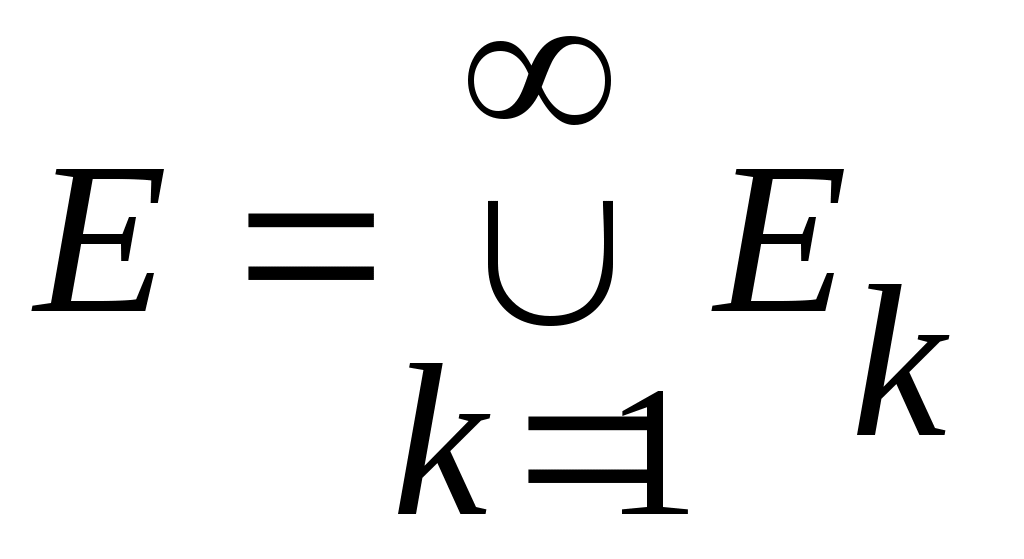 болсын. болсын. 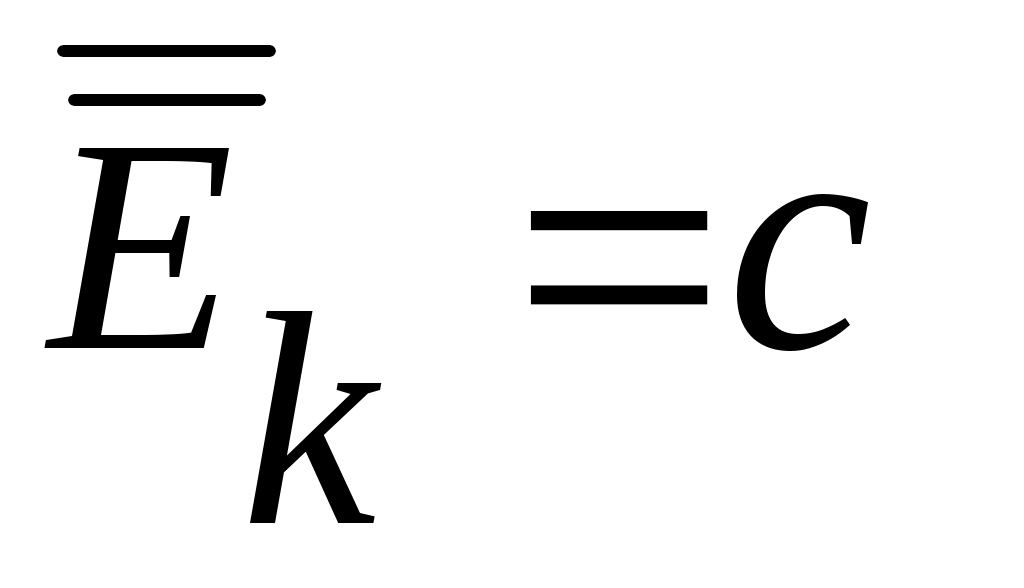 теңдігі бойынша әрбір теңдігі бойынша әрбір 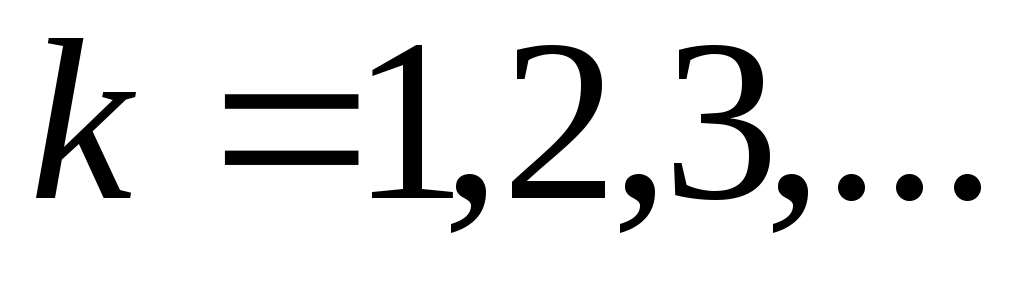 үшін үшін 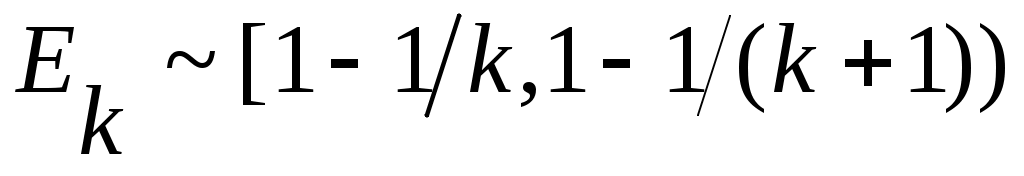 . Енді . Енді 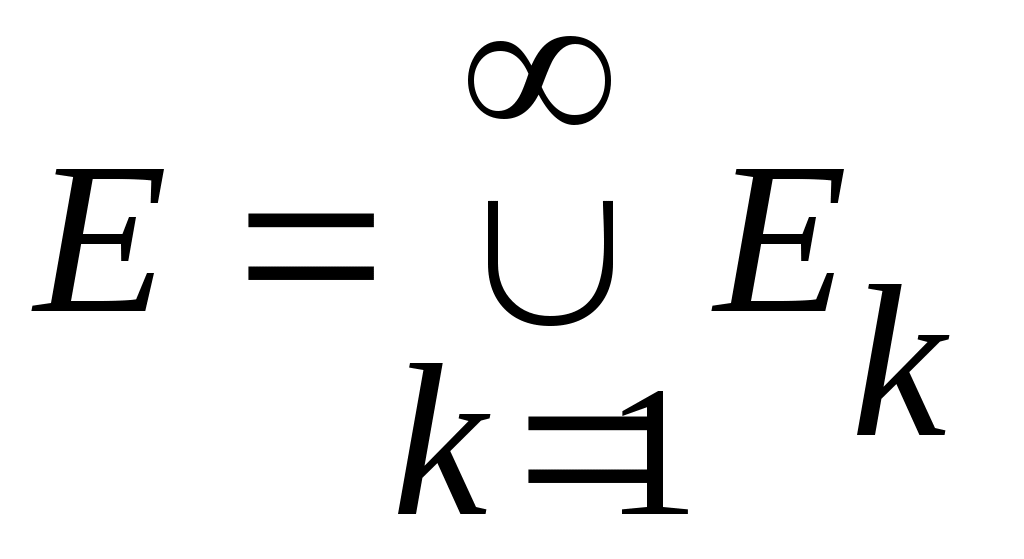 және және
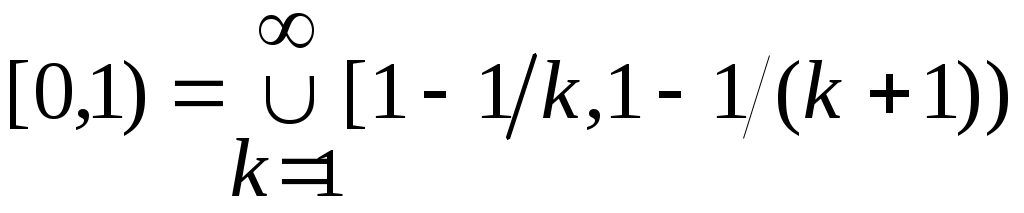 теңдіктерін ескеріп, 2 – теореманы (§2) қолдансақ болғаны. теңдіктерін ескеріп, 2 – теореманы (§2) қолдансақ болғаны.
Келесі теоремада саналымды да емес, континуалды да емес ақырсыз жиын бар екені көрсетіледі.
7 – теорема. 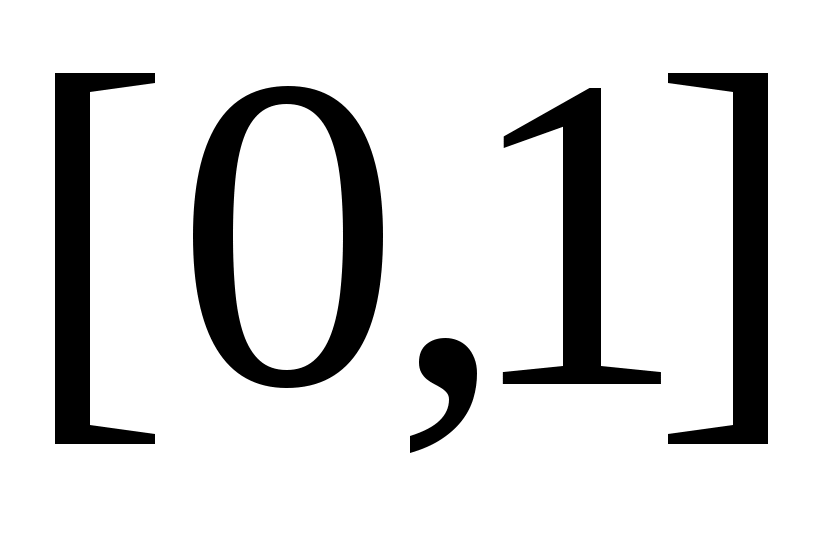 сегментінде анықталған барлық функциялардың сегментінде анықталған барлық функциялардың 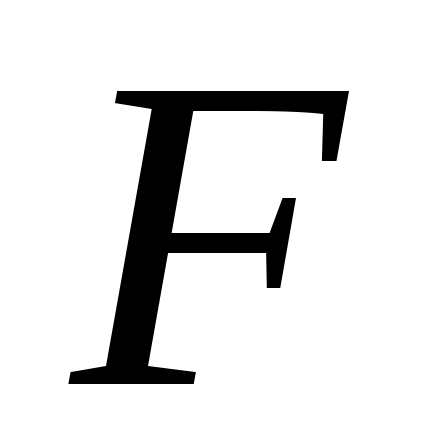
жиыны саналымды жиын да, континуалды жиын да емес.
Дәлелдеуі. 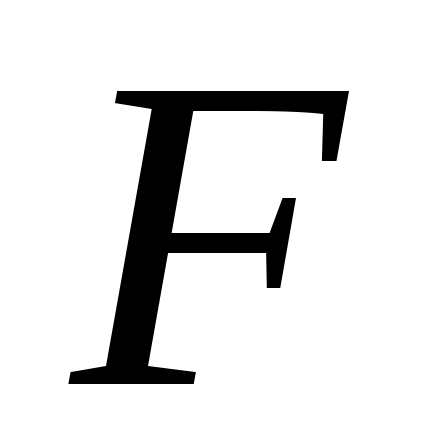 жиынының саналымды жиын емес екеніне көз жеткізейік. Кері жорып, « жиынының саналымды жиын емес екеніне көз жеткізейік. Кері жорып, «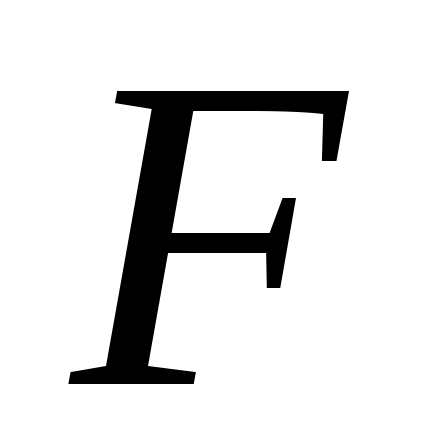 жиыны – саналымды жиын» дейік. Енді жиыны – саналымды жиын» дейік. Енді
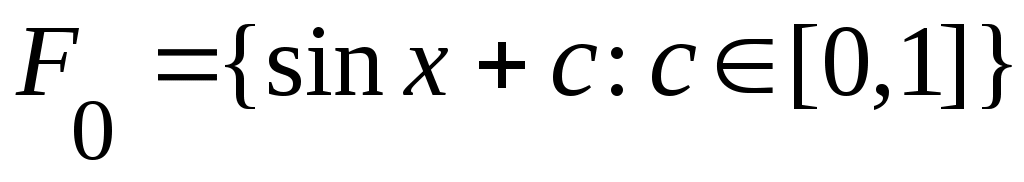 жиынын қарастырсақ, қайшылық аламыз. Бір жағынан, жиынын қарастырсақ, қайшылық аламыз. Бір жағынан, 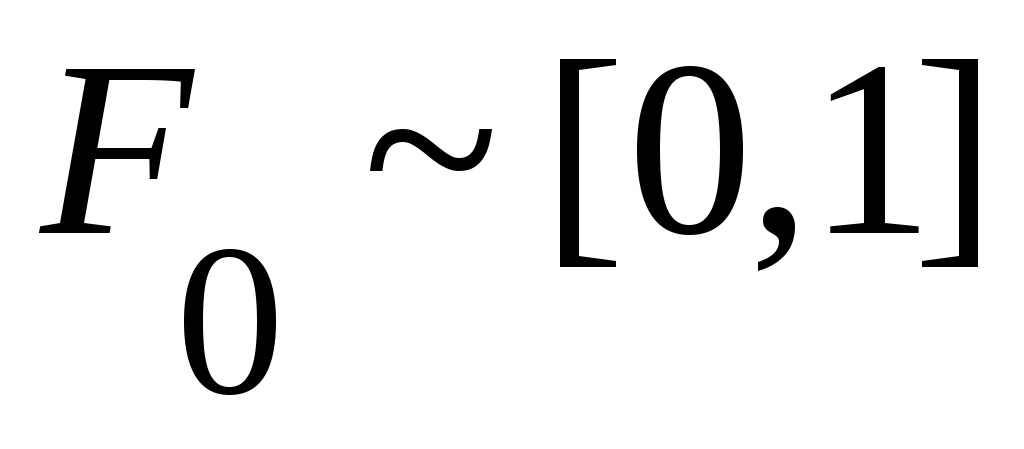 эквиваленттілігі мен 1– теорема (§3) бойынша эквиваленттілігі мен 1– теорема (§3) бойынша 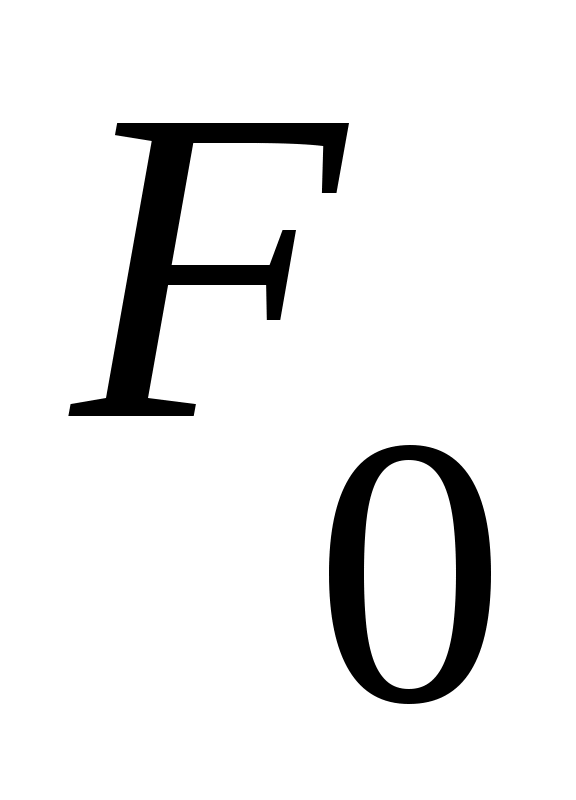 жиыны саналымды жиын емес. Екінші жағынан, жиыны саналымды жиын емес. Екінші жағынан, 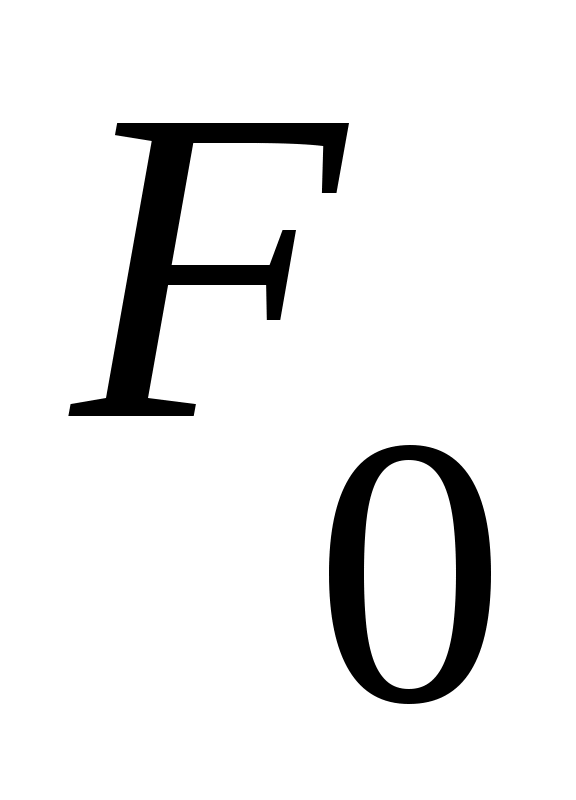 жиыны – саналымды жиыны – саналымды 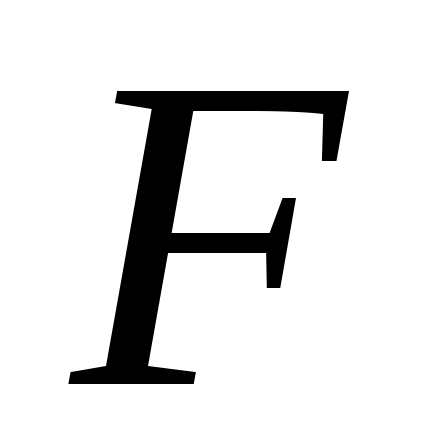 жиынының ақырсыз жиыншасы ретінде 7 – теорема (§3) бойынша саналымды жиын. Демек, жиынының ақырсыз жиыншасы ретінде 7 – теорема (§3) бойынша саналымды жиын. Демек, 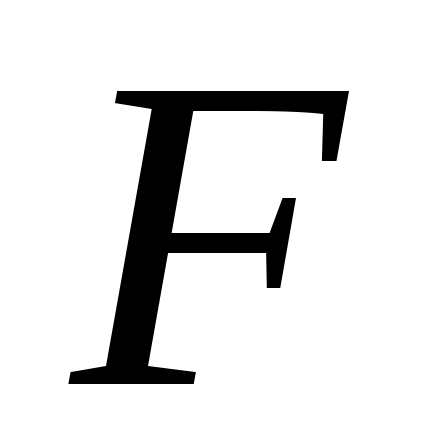 жиыны саналымды жиын емес. жиыны саналымды жиын емес.
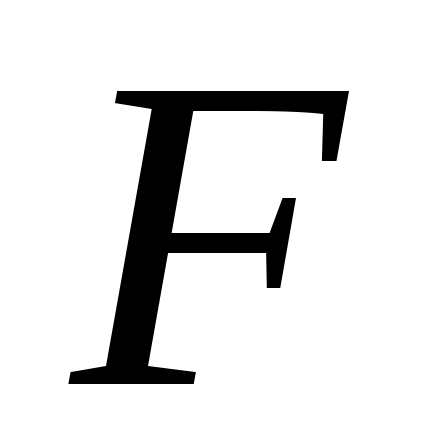 жиынының континуалды жиын емес екеніне көз жеткізейік. Кері жорып, жиынының континуалды жиын емес екеніне көз жеткізейік. Кері жорып, 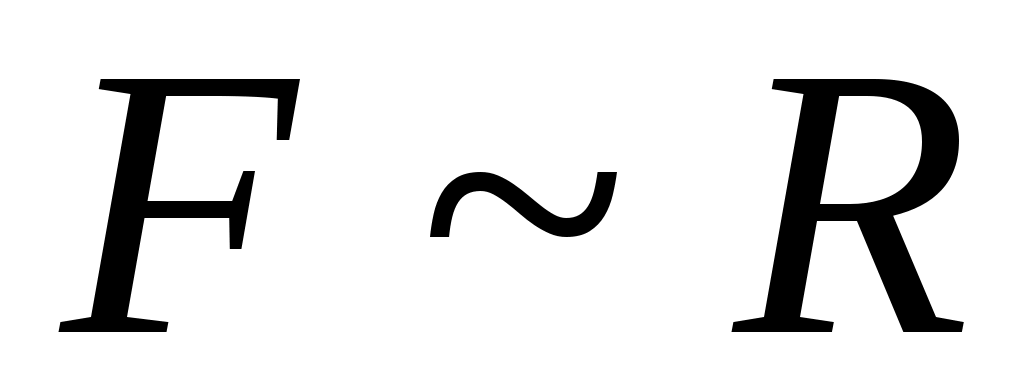 эквиваленттілігі орындалады дейік. 1 – теорема бойынша эквиваленттілігі орындалады дейік. 1 – теорема бойынша 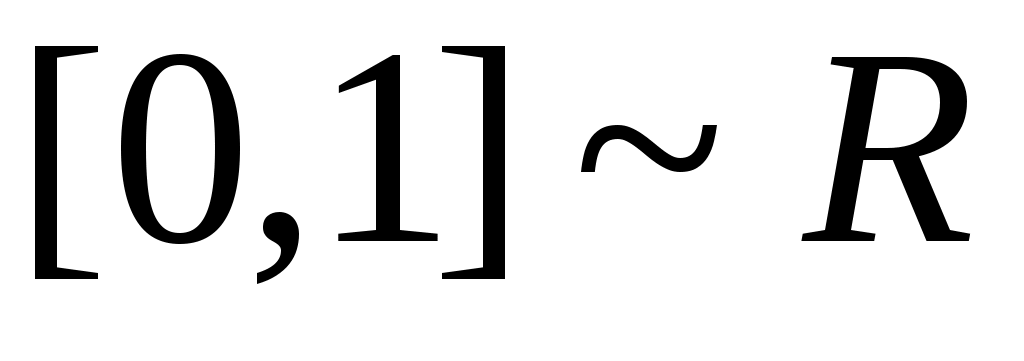 . Демек, 2 – параграфтағы 1 – теоремаға жүгінсек, . Демек, 2 – параграфтағы 1 – теоремаға жүгінсек, 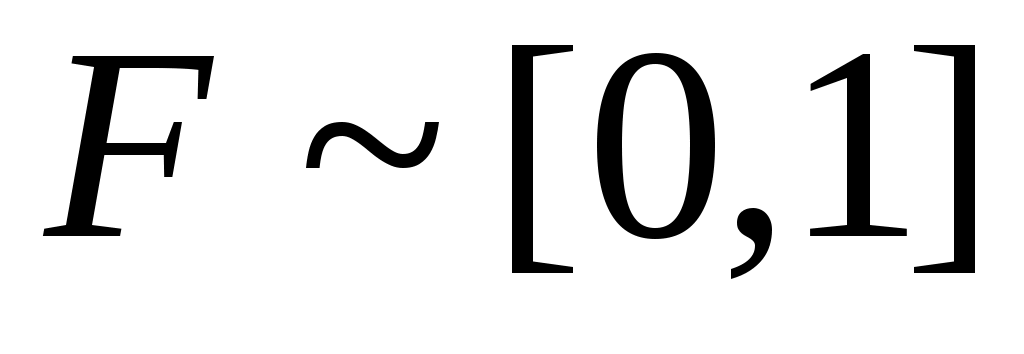 . . 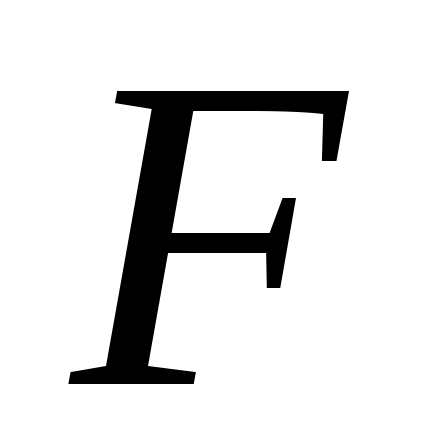 жиынының жиынының 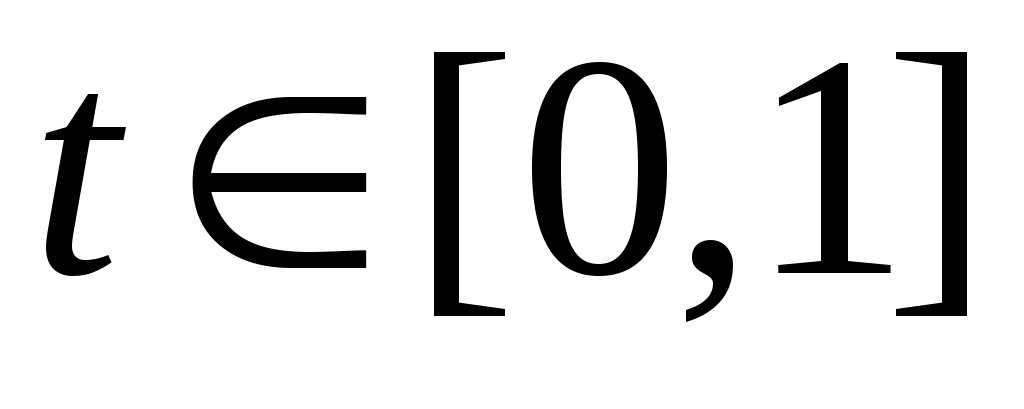 нүктеге сәйкес элементін нүктеге сәйкес элементін 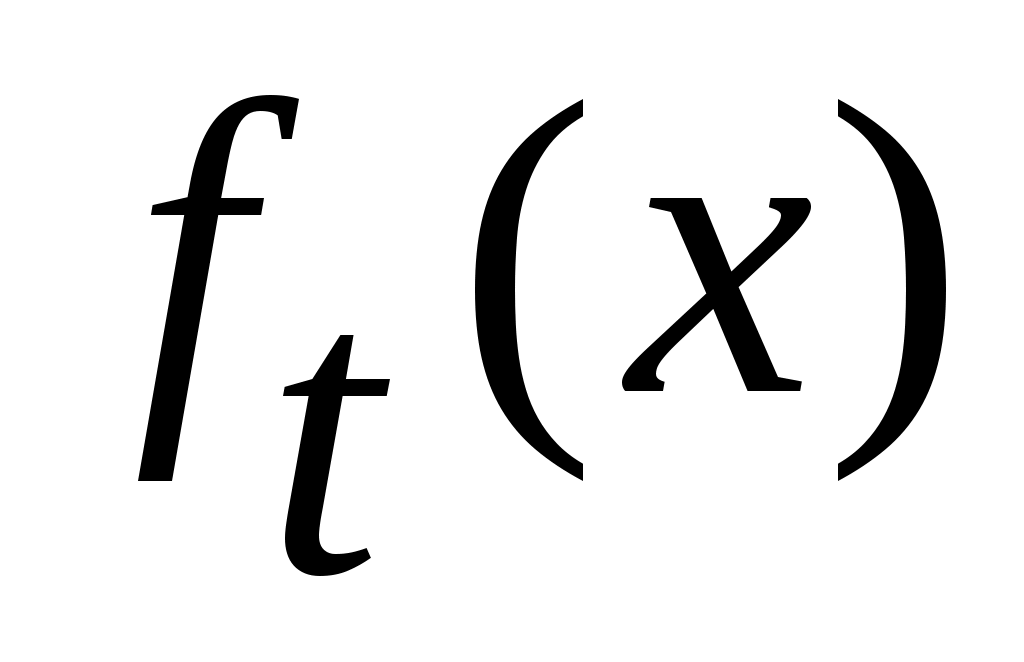 арқылы белгілеп, арқылы белгілеп, 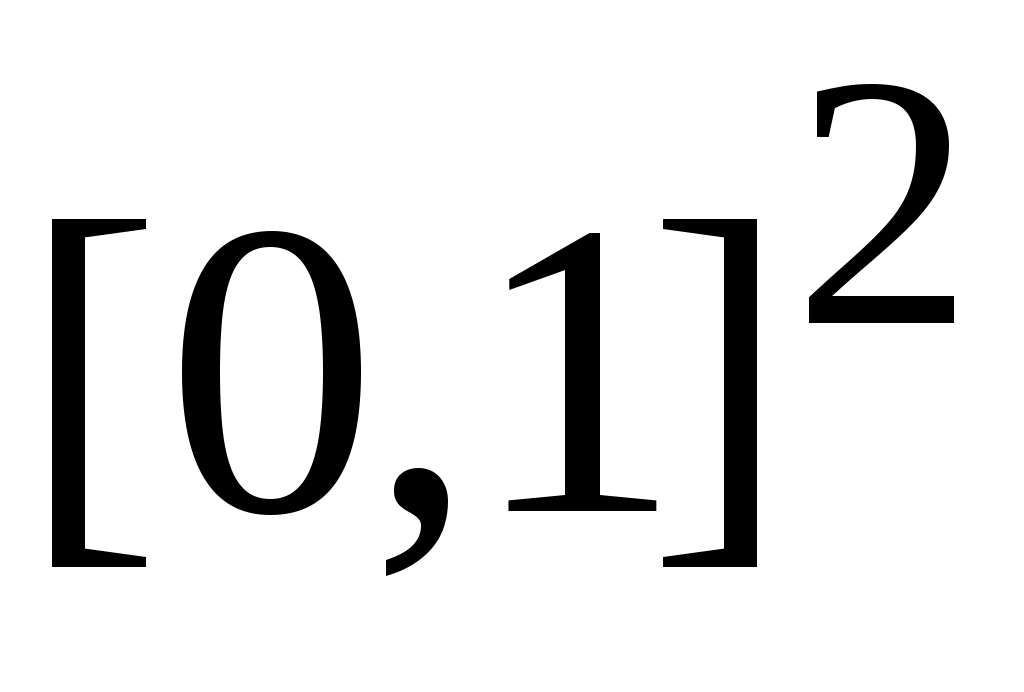 квадратында анықталған квадратында анықталған 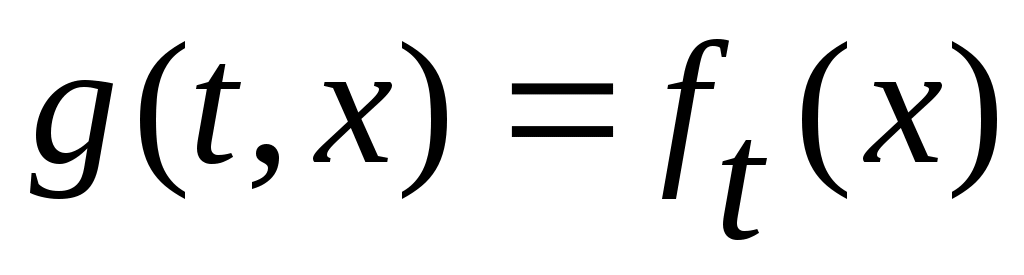 функциясын қарастырайық. функциясын қарастырайық. 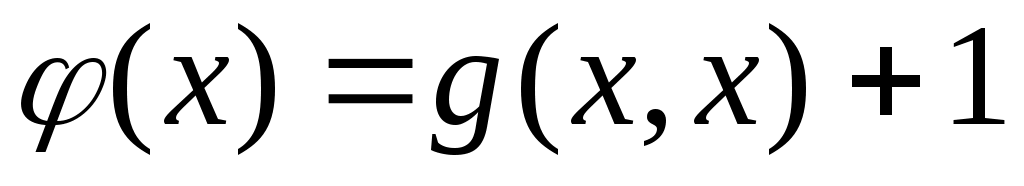 функциясы функциясы 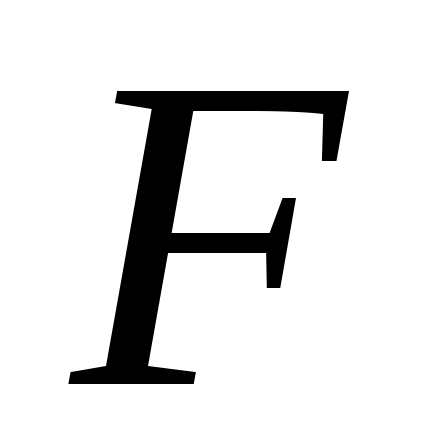 жиынында жататындықтан, қайсыбір жиынында жататындықтан, қайсыбір 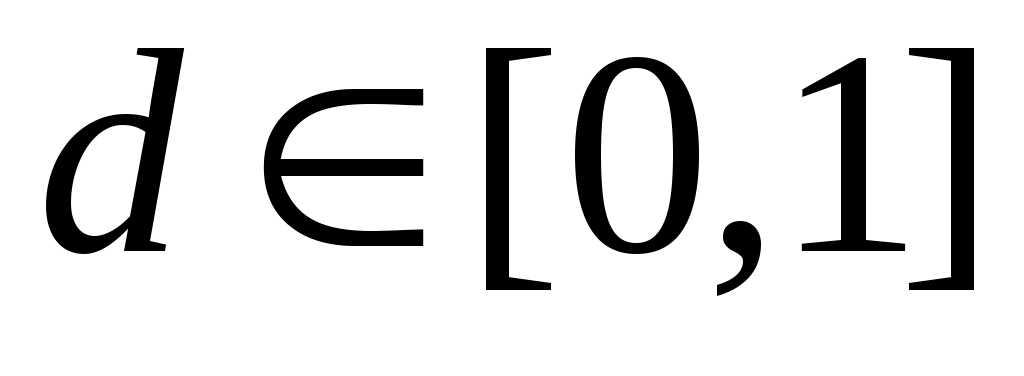 саны үшін саны үшін 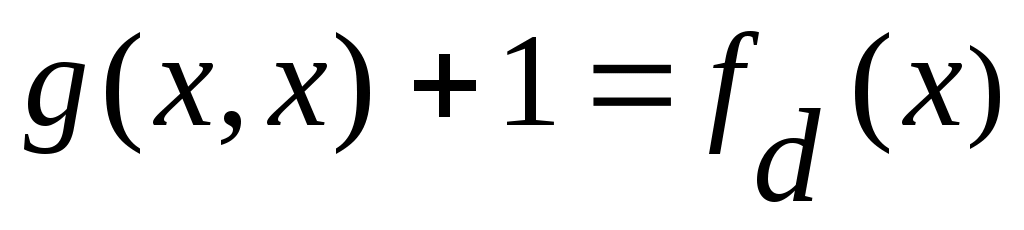 теңдігі орындалады. Соңғы теңдіктегі теңдігі орындалады. Соңғы теңдіктегі 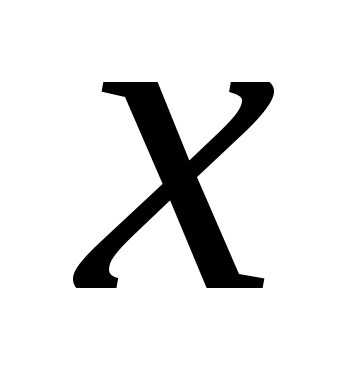 саны ретінде саны ретінде 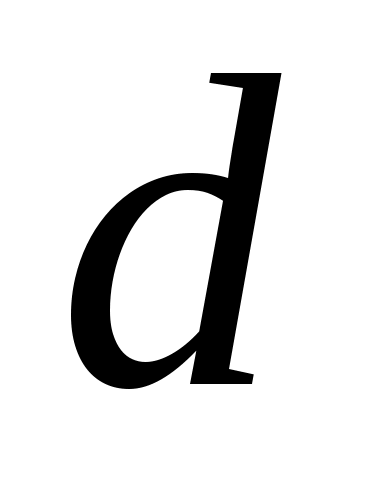 санын алсақ, қайшылыққа келеміз: санын алсақ, қайшылыққа келеміз:
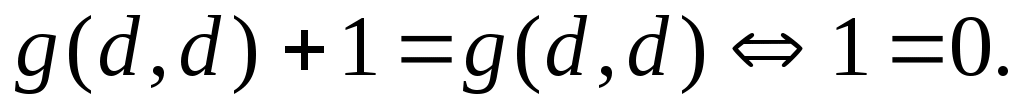
Демек, 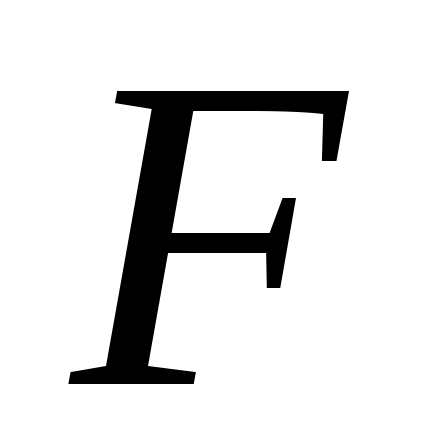 жиыны континуалды жиын емес. Сонымен, жиыны континуалды жиын емес. Сонымен, 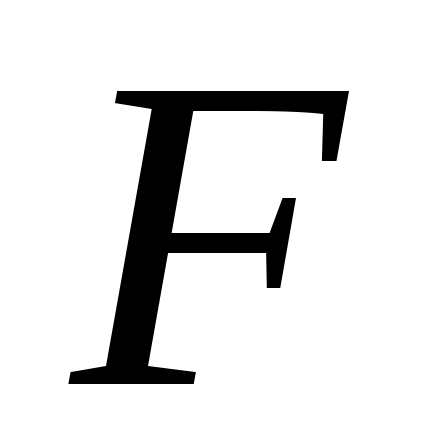 жиыны саналымды жиын да, континуалды жиын да емес екен. жиыны саналымды жиын да, континуалды жиын да емес екен.
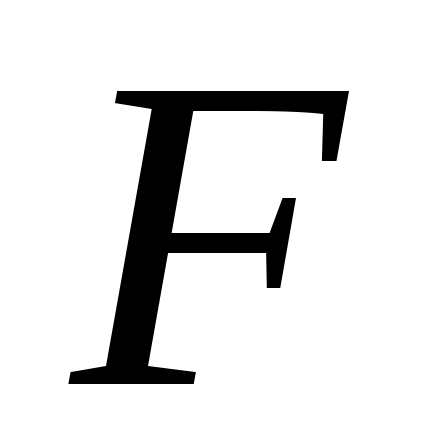 жиынының қуатын жиынының қуатын 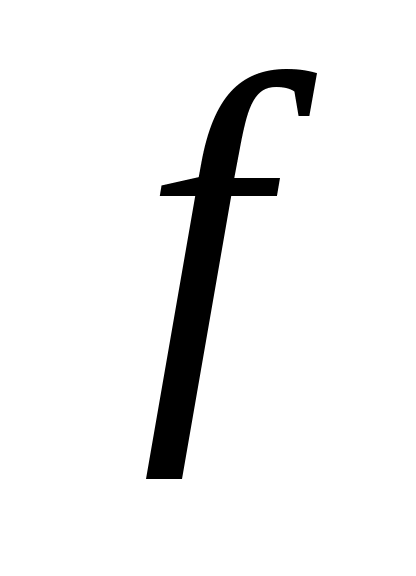 әрпімен белгілеу қалыптасқан, яғни, әрпімен белгілеу қалыптасқан, яғни, 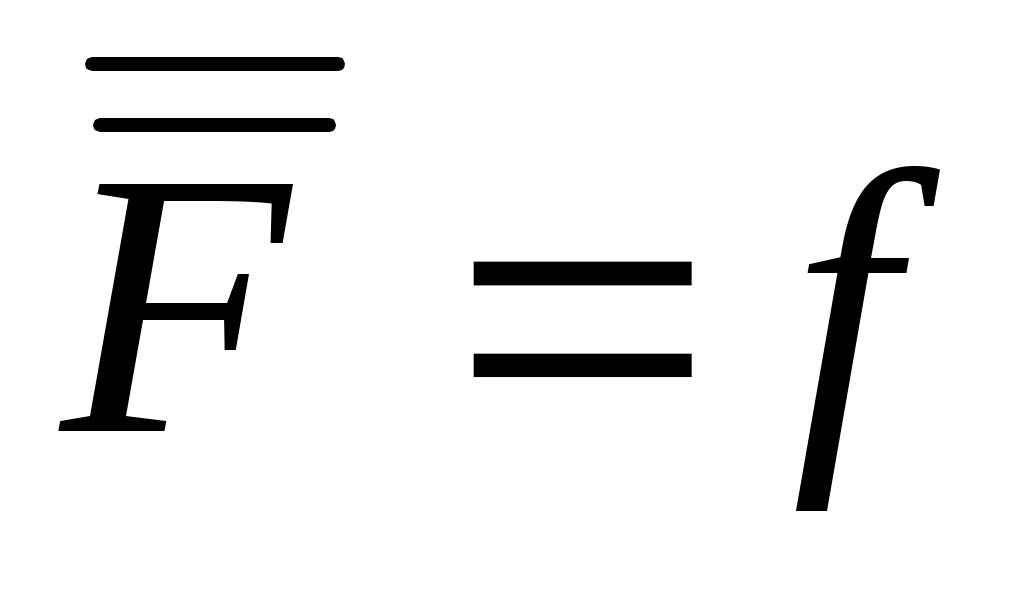 . .
|
|
|
 Скачать 1.5 Mb.
Скачать 1.5 Mb.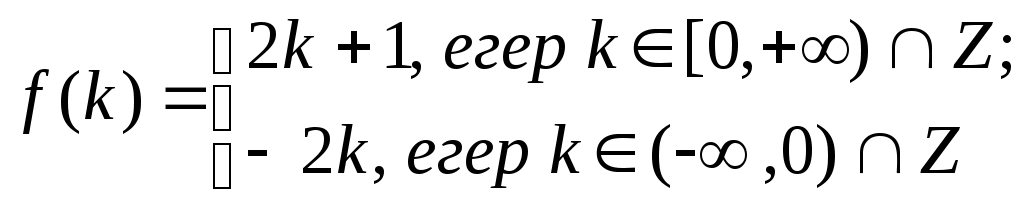 теңдігін қанағаттандыратын
теңдігін қанағаттандыратын 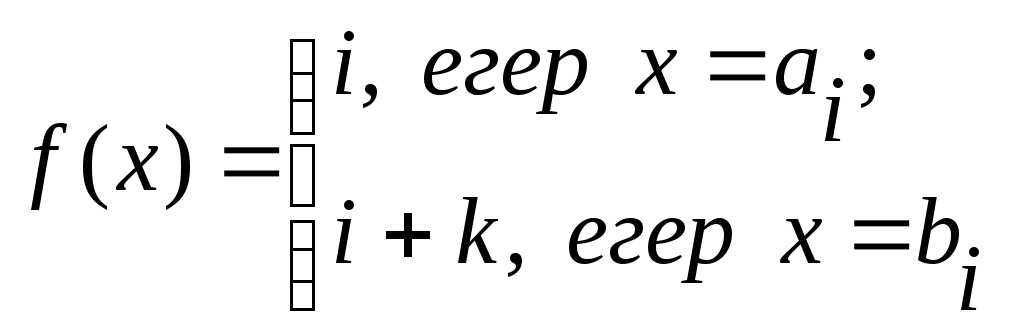 теңдігін қанағаттандыратын
теңдігін қанағаттандыратын 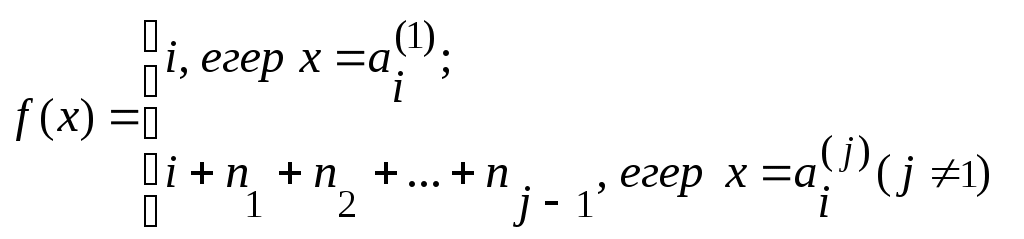 теңдігі бойынша
теңдігі бойынша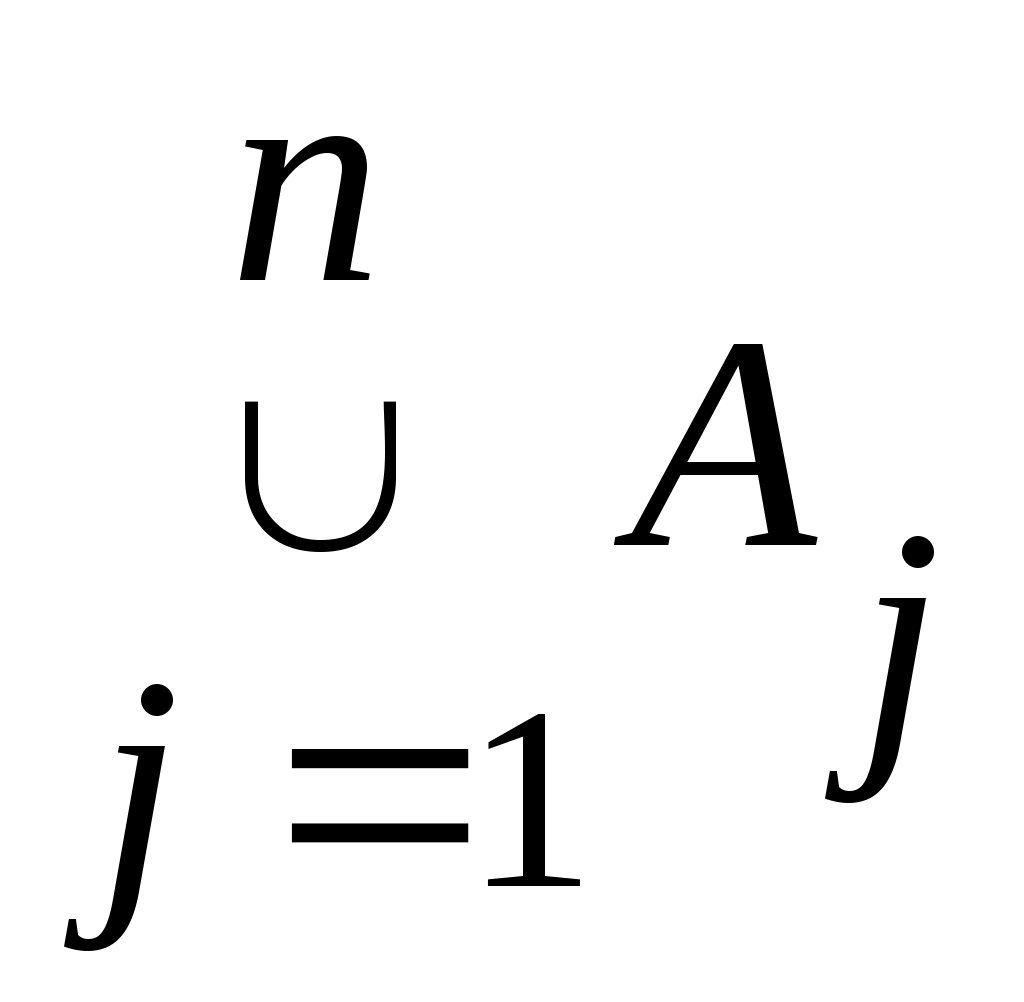 жиыны саналымды жиын болады.
жиыны саналымды жиын болады.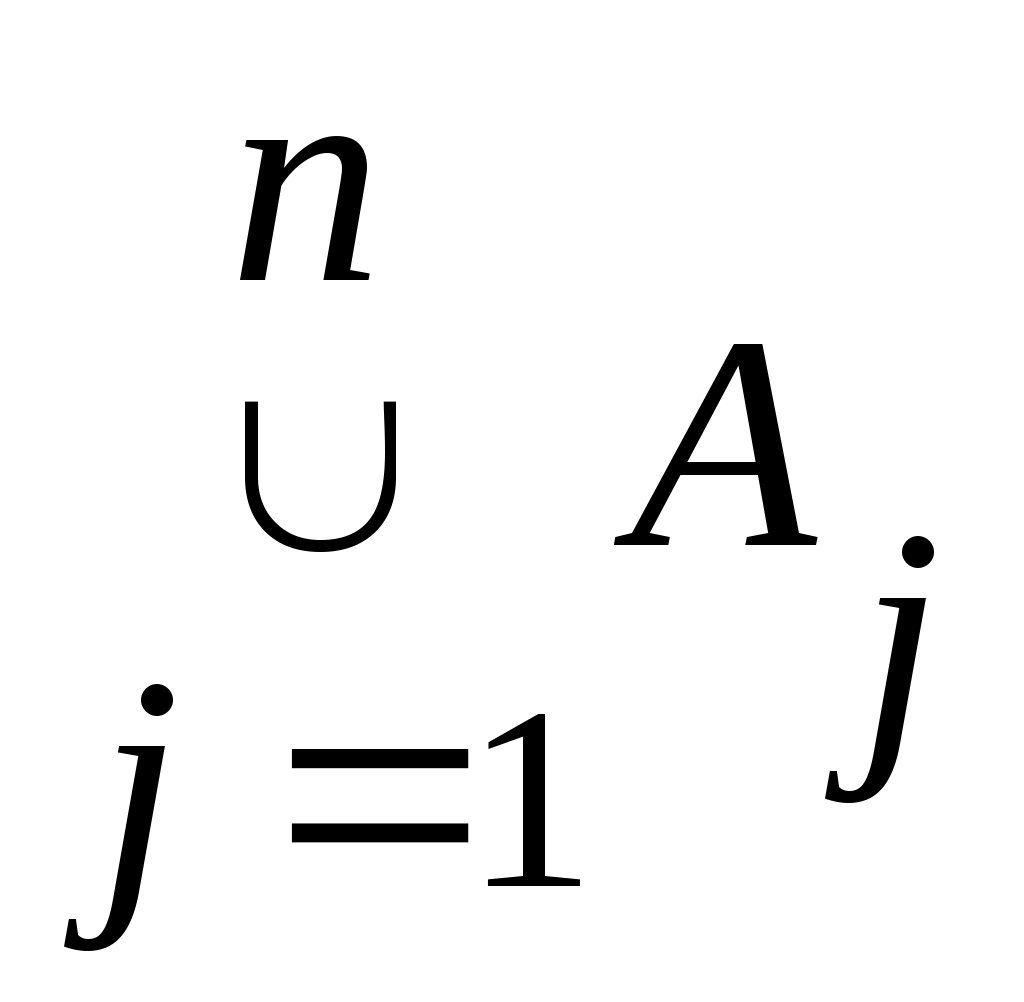 жиыны
жиыны 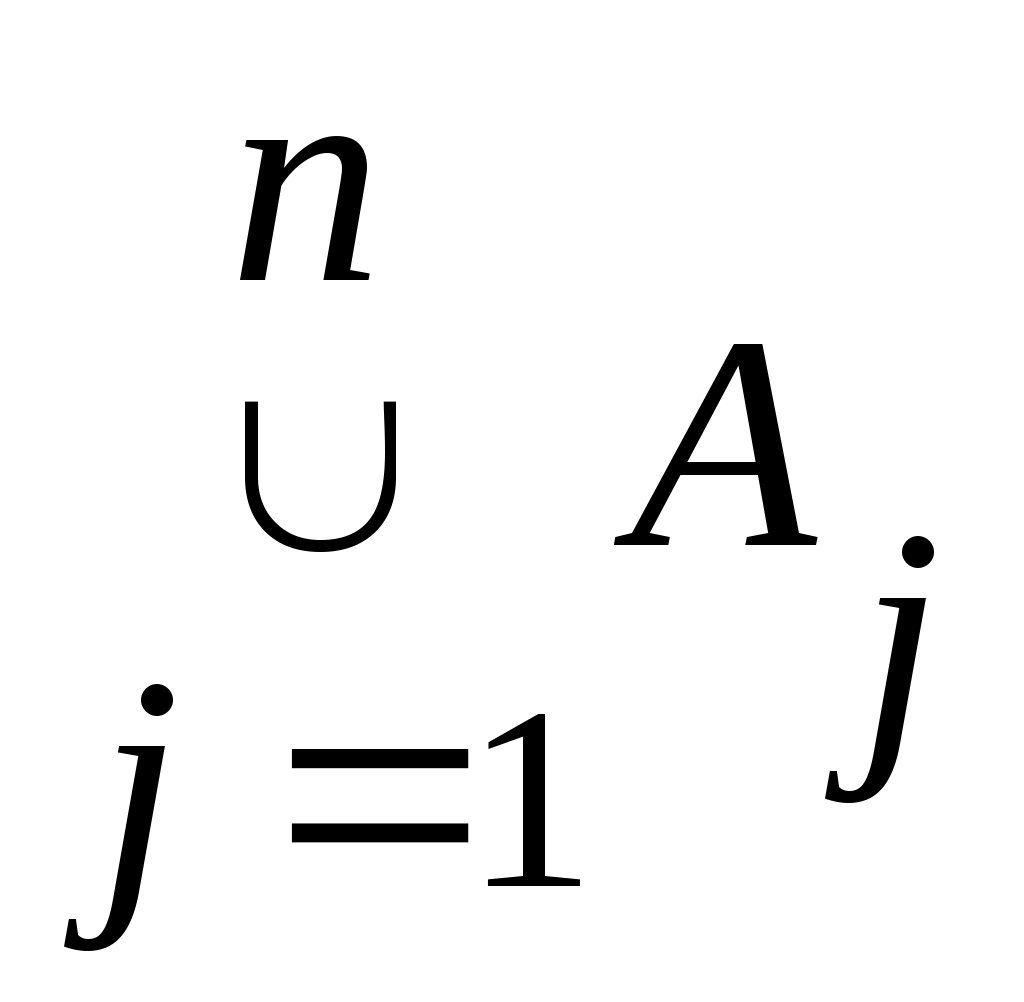 жиыны – саналымды жиын.
жиыны – саналымды жиын.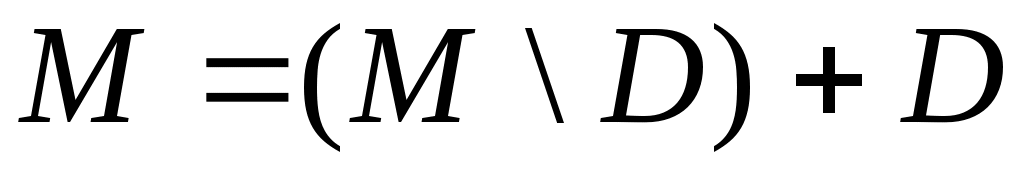 және
және 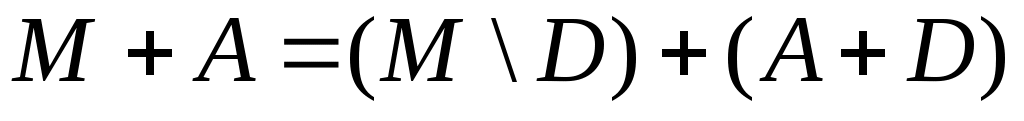 теңдіктерінің оң жақтарына зер салайық:
теңдіктерінің оң жақтарына зер салайық: 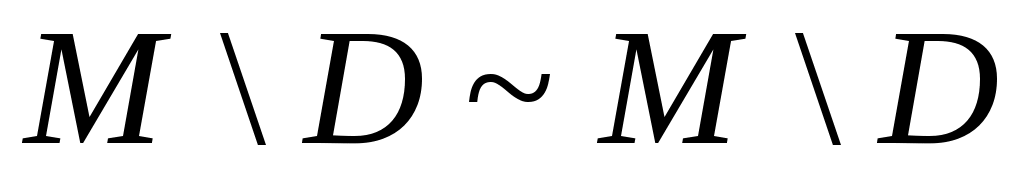 және
және 
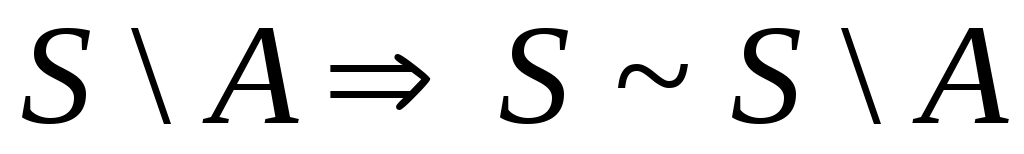 .
.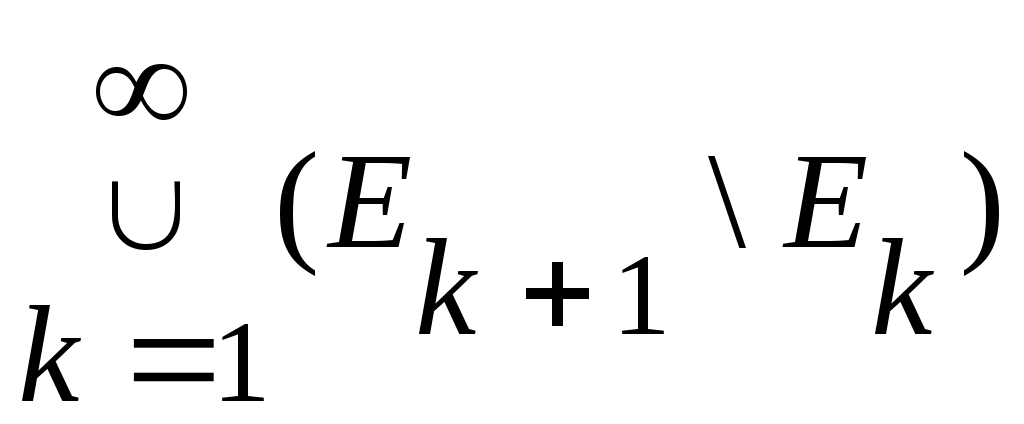 ,
, 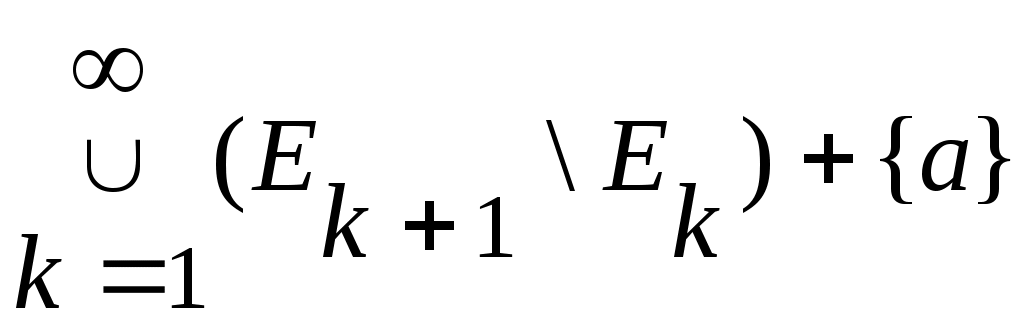 ,
,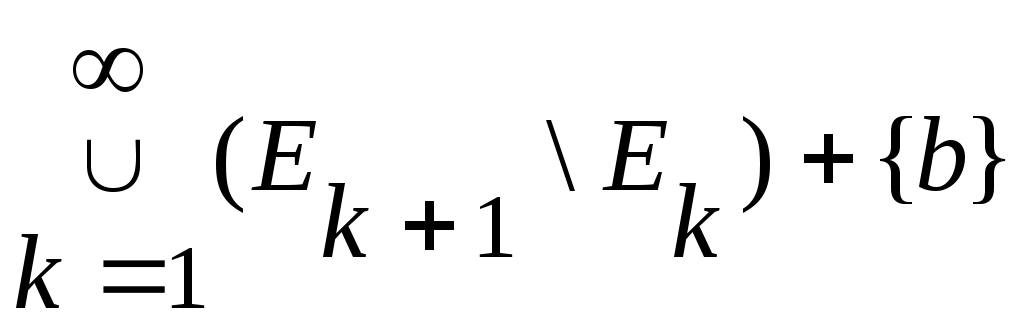 ,
, 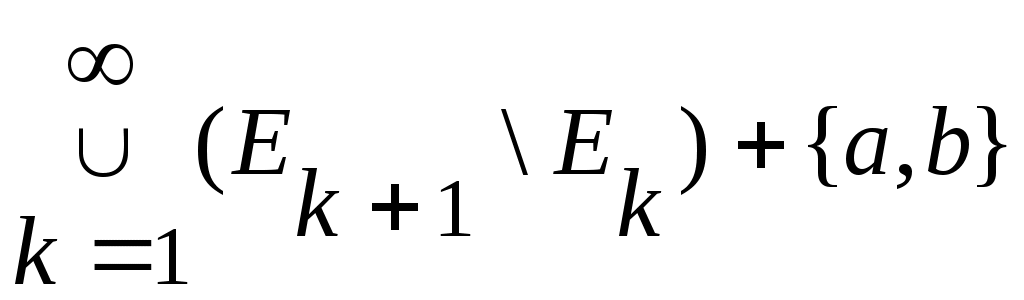 жиындарының бірімен беттеседі (Осыны тексеріңіз).
жиындарының бірімен беттеседі (Осыны тексеріңіз).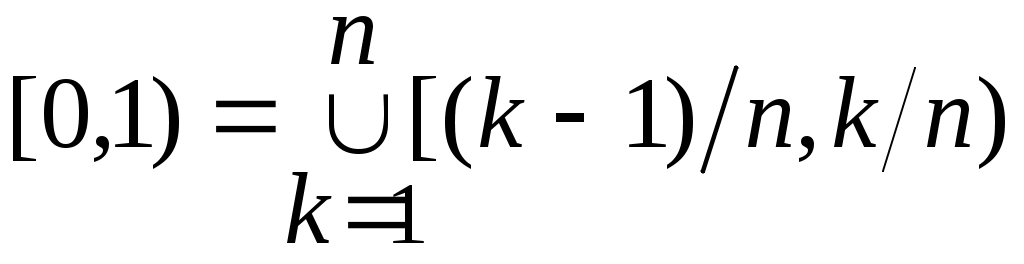 теңдіктерін ескеріп, 2 – теореманы (§2) қолдансақ
теңдіктерін ескеріп, 2 – теореманы (§2) қолдансақ