|
|
ГЛ1. 1 тарау. Жиындар теориясыны элементтері жиыны жиыныны жиыншасы болан жадайда жиыны жиынын амтиды
§5. Сандық түзудегі тұйық, ашық жиындар
1 – анықтама.  нүктесінің маңайы деп осы нүктені қамтитын кез нүктесінің маңайы деп осы нүктені қамтитын кез
келген интервалды атаймыз және оны 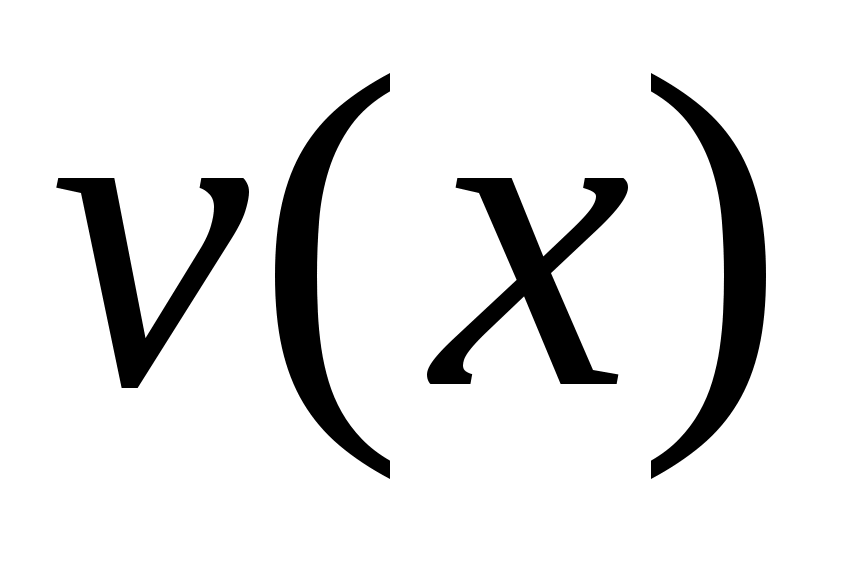 арқылы белгілейміз. арқылы белгілейміз.
Сонымен,  нүктесінің маңайы деп ұштары нүктесінің маңайы деп ұштары 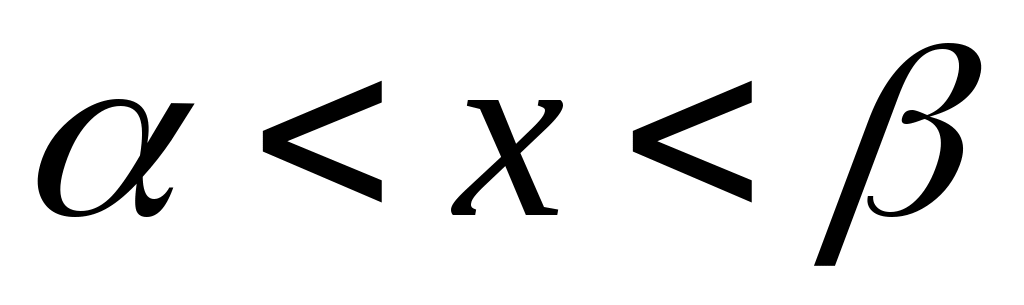 теңсіздіктерін қанағаттандыратын теңсіздіктерін қанағаттандыратын 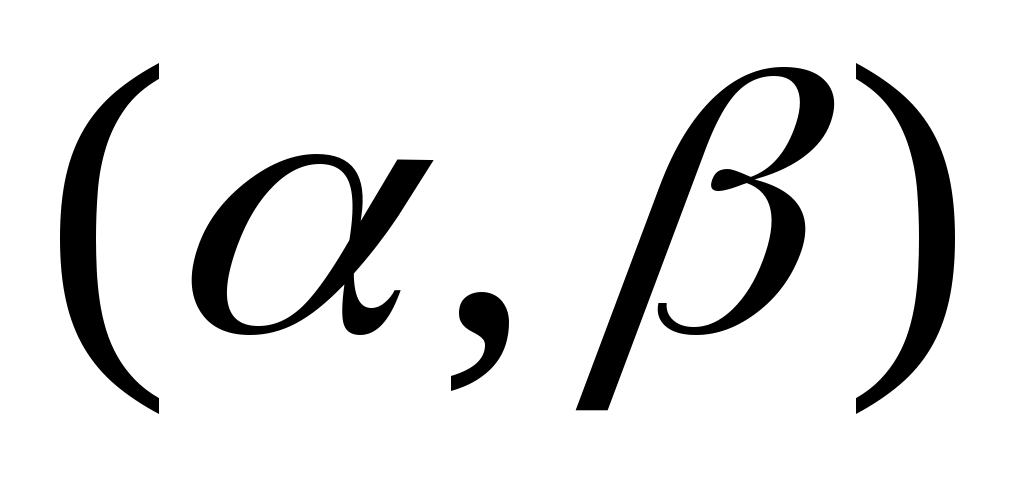 интервалы аталады. интервалы аталады.
2 – анықтама.  нүктесі және нүктесі және  жиыны берілсін. Егер жиыны берілсін. Егер 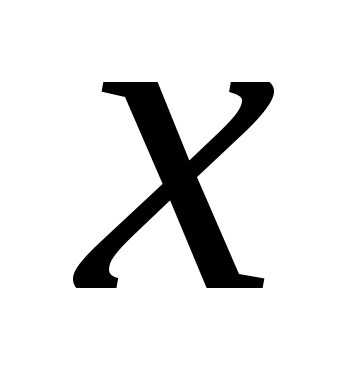 нүктесінің әрбір маңайында нүктесінің әрбір маңайында  жиынының жиынының 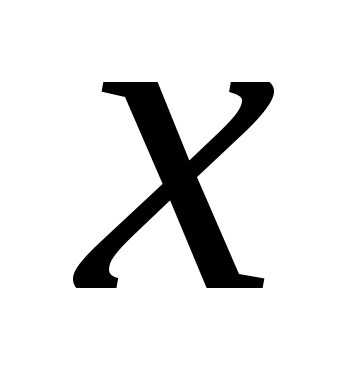 нүктесінен өзге қайсыбір нүктесі жататын болса, онда нүктесінен өзге қайсыбір нүктесі жататын болса, онда 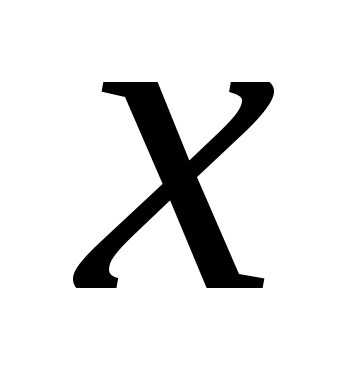 нүктесін « нүктесін « жиынының шектік нүктесі» деп атаймыз. жиынының шектік нүктесі» деп атаймыз.
2 – анықтама былай да айтылады: Егер 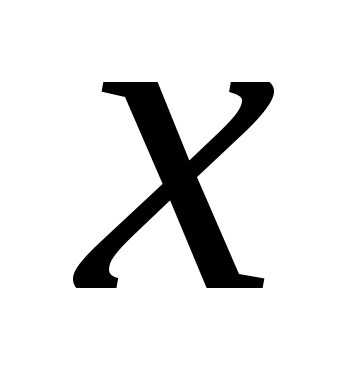 нүктесінің кез келген маңайы мен нүктесінің кез келген маңайы мен 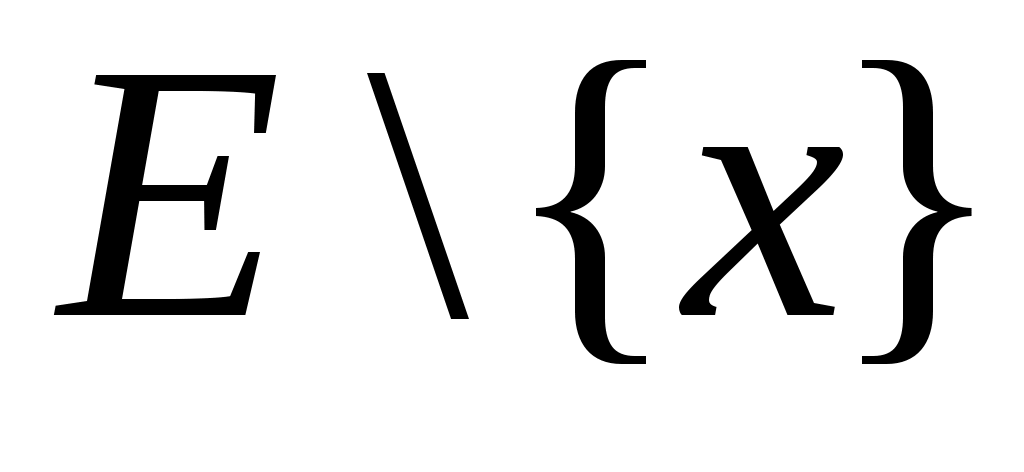 жиынының қиылысуы бос жиын болмаса, онда жиынының қиылысуы бос жиын болмаса, онда 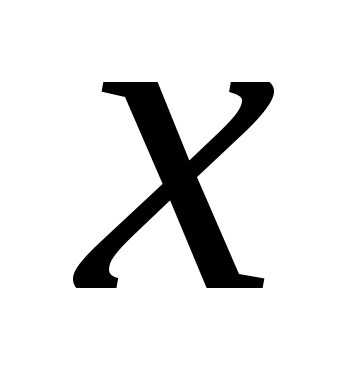 нүктесін « нүктесін « жиынының шектік нүктесі» деп атаймыз. жиынының шектік нүктесі» деп атаймыз.
1– ескерту. Шектік нүкте жиында жатуы да, жатпауы да мүмкін. Мәселен, 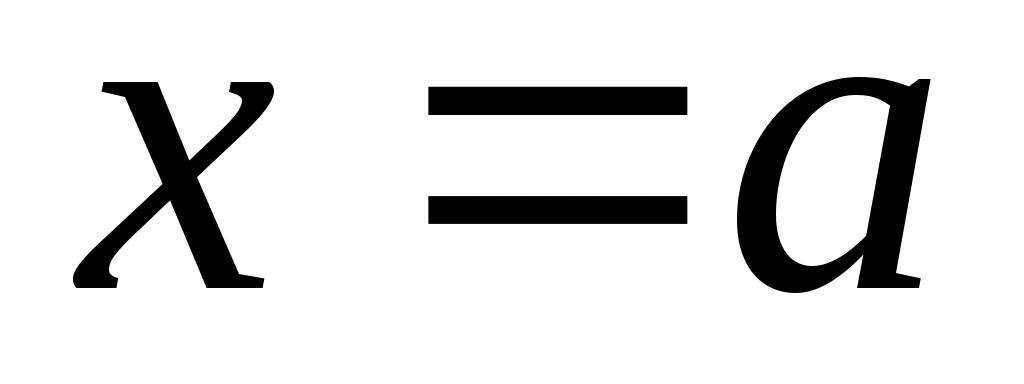 нүктесі нүктесі 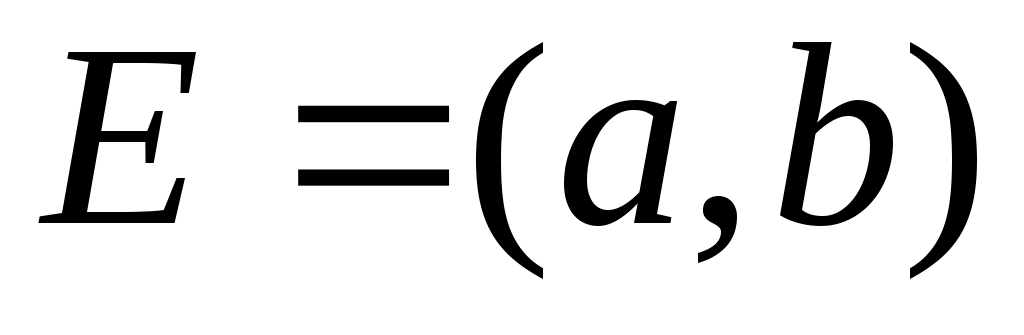 жиынының шектік нүктесі және жиынының шектік нүктесі және 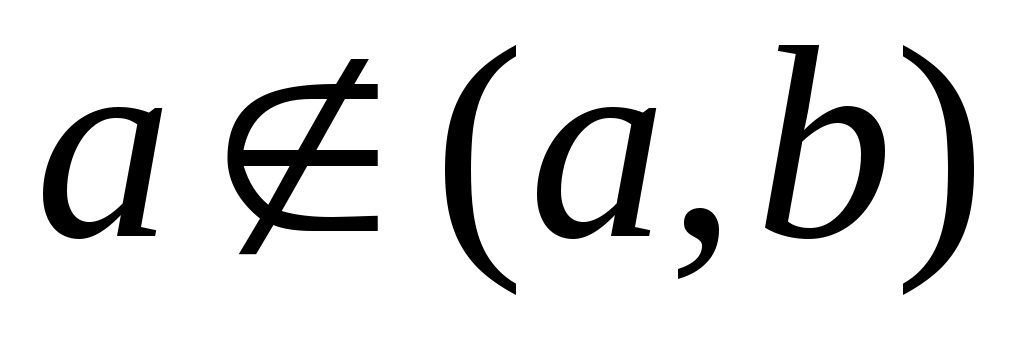 . . 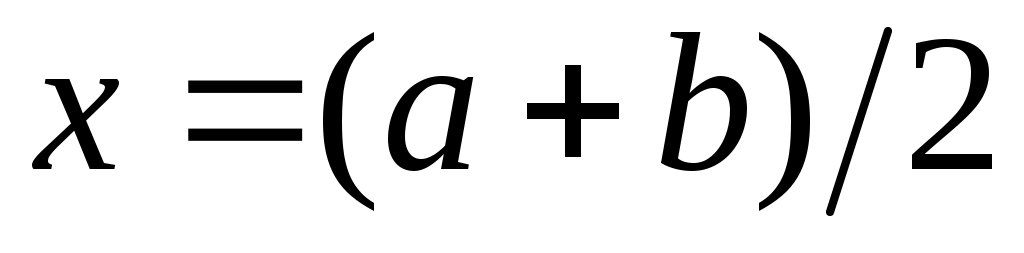 нүктесі де нүктесі де 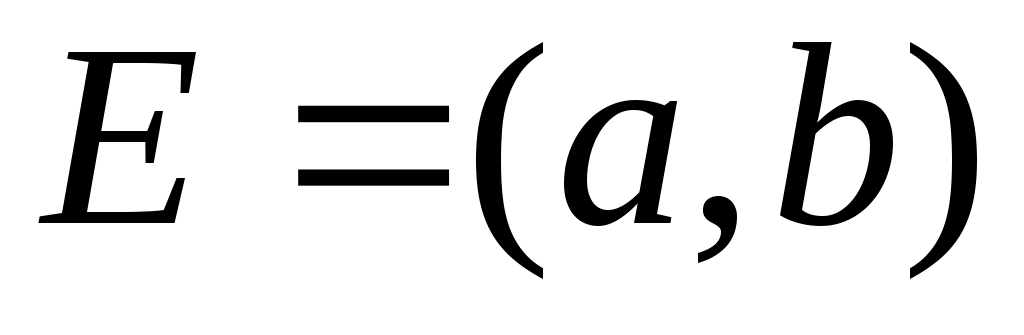 жиынының шектік нүктесі, бірақ жиынының шектік нүктесі, бірақ 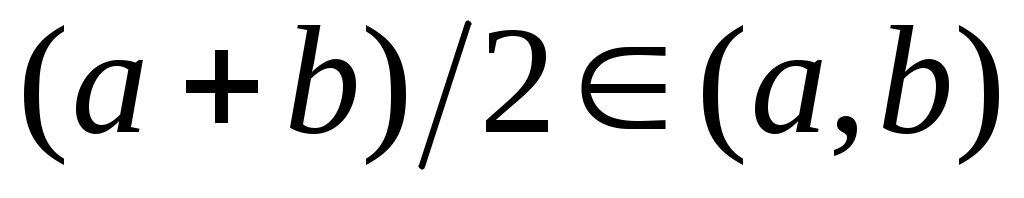 . .
2 – ескерту. Шектік нүктесі жоқ жиындар бар. Мәселен, кез келген ақырлы жиынның шектік нүктесі жоқ.
Енді шектік нүктенің кейбір қасиеттерін келтірейік.
1 – теорема. Егер 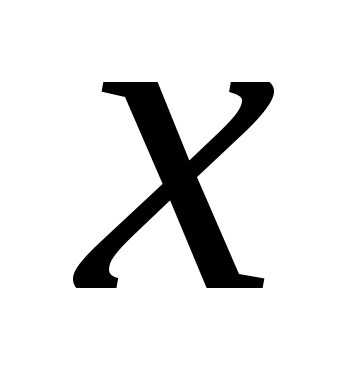 нүктесі нүктесі  жиынының шектік нүктесі болса, онда кез келген жиынының шектік нүктесі болса, онда кез келген 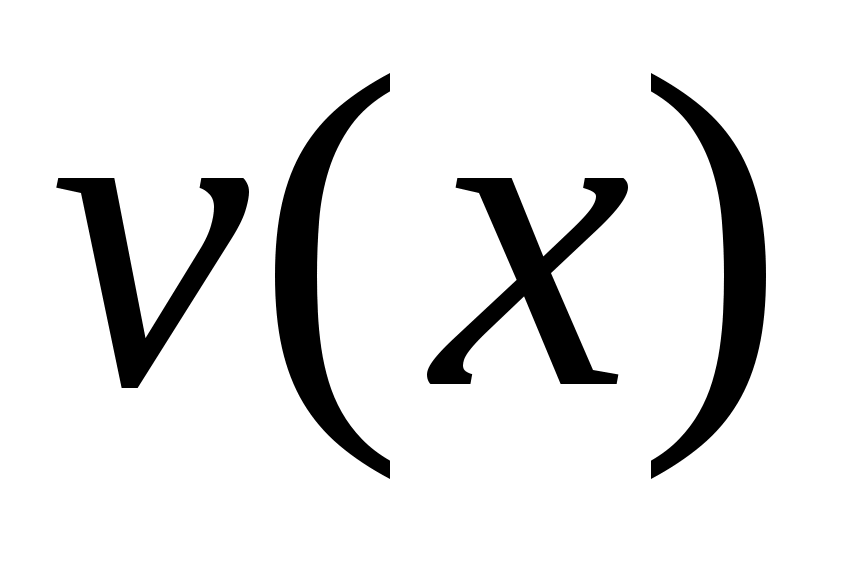 маңайының маңайының  жиынымен қиылысуы ақырсыз жиын болады. жиынымен қиылысуы ақырсыз жиын болады.
Дәлелдеуі. Кері жорып, қайсыбір 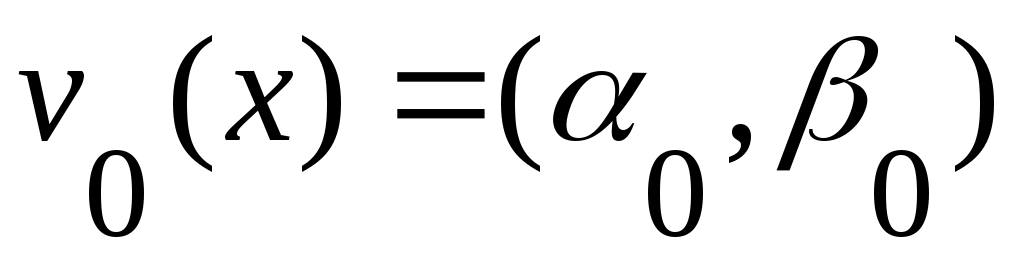 маңайының маңайының  жиынымен қиылысуыақырлы жиын болады дейік. Енді жиынымен қиылысуыақырлы жиын болады дейік. Енді 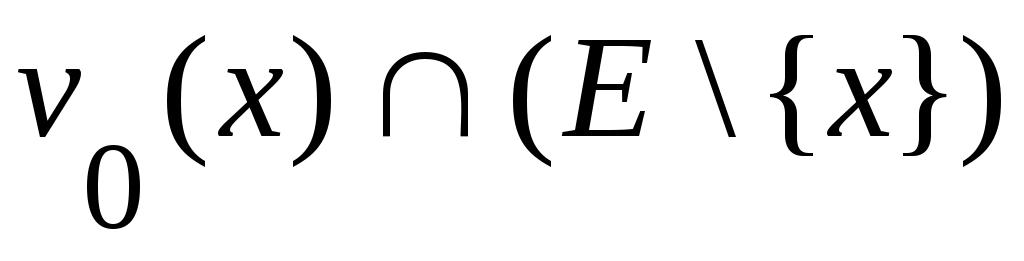 жиынының элементтерін жиынының элементтерін 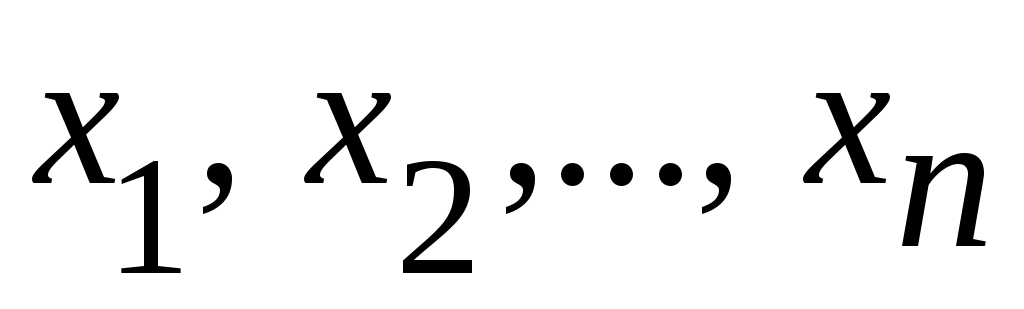 арқылы белгілеп, арқылы белгілеп,
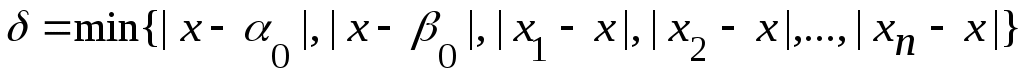
санын анықтасақ, 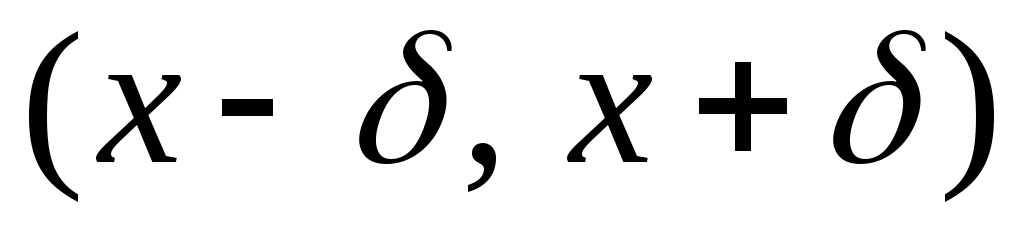 интервалының интервалының 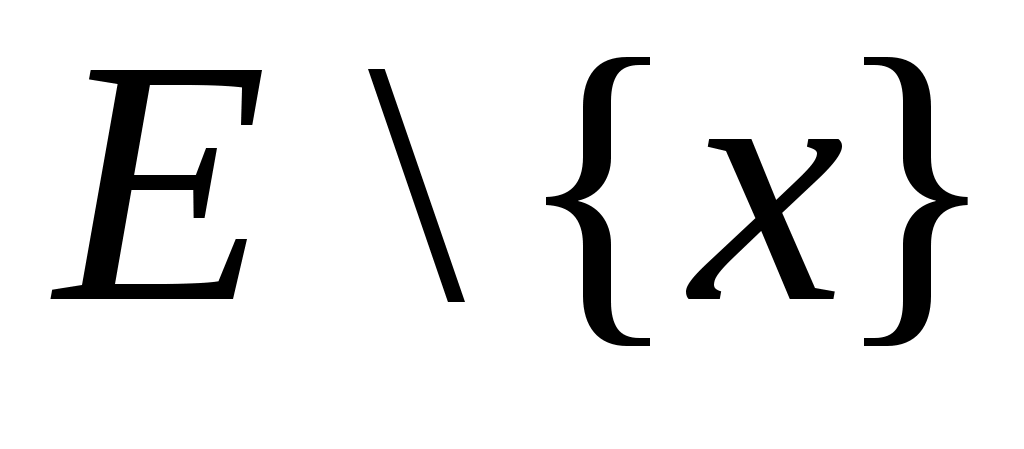 жиынымен қиылысуы бос жиын болар еді. Бұл « жиынымен қиылысуы бос жиын болар еді. Бұл « нүктесі – нүктесі –  жиынының шектік нүктесі» деген тұжырымға қайшы. жиынының шектік нүктесі» деген тұжырымға қайшы.
Бұл теорема былай да айтылады: Егер 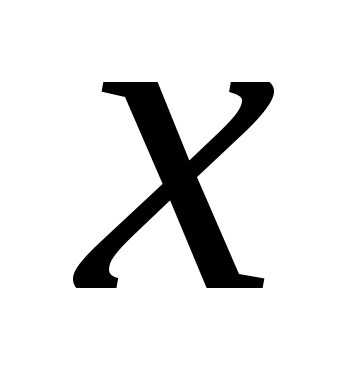 нүктесі нүктесі  жиынының шектік нүктесі болса, онда жиынының шектік нүктесі болса, онда 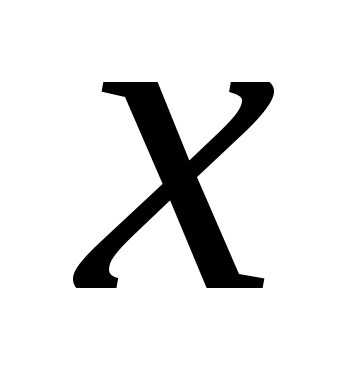 нүктесінің әрбір маңайында нүктесінің әрбір маңайында  жиынының шексіз көп нүктесі жатады. жиынының шексіз көп нүктесі жатады.
2 – теорема. Егер 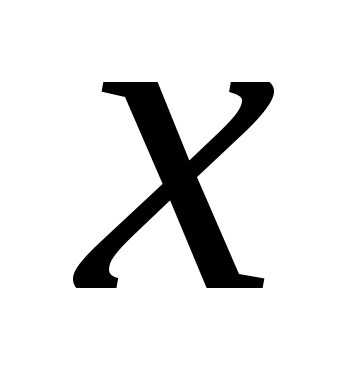 нүктесі нүктесі  жиынының шектік нүктесі болса, онда жиынының шектік нүктесі болса, онда 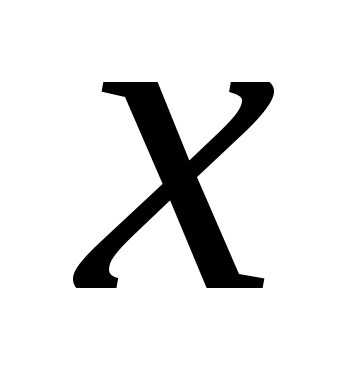 нүктесіне жинақталатын нүктесіне жинақталатын 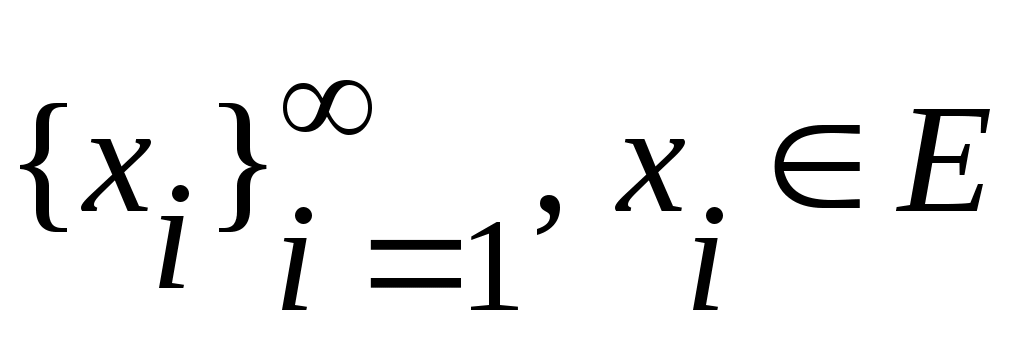 тізбегі табылады. тізбегі табылады.
Дәлелдеуі. 1 – жағдай: Егер 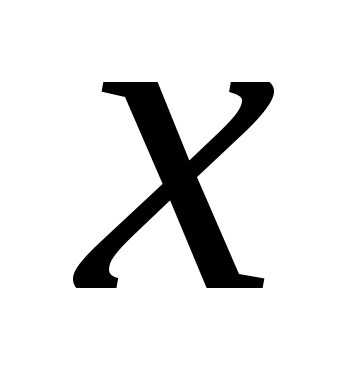 нүктесі нүктесі  жиынында жататын болса, онда әрбір мүшесі жиынында жататын болса, онда әрбір мүшесі 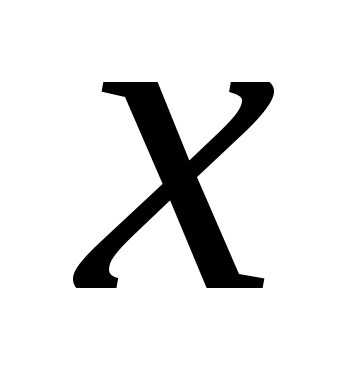 нүктесі болатын нүктесі болатын 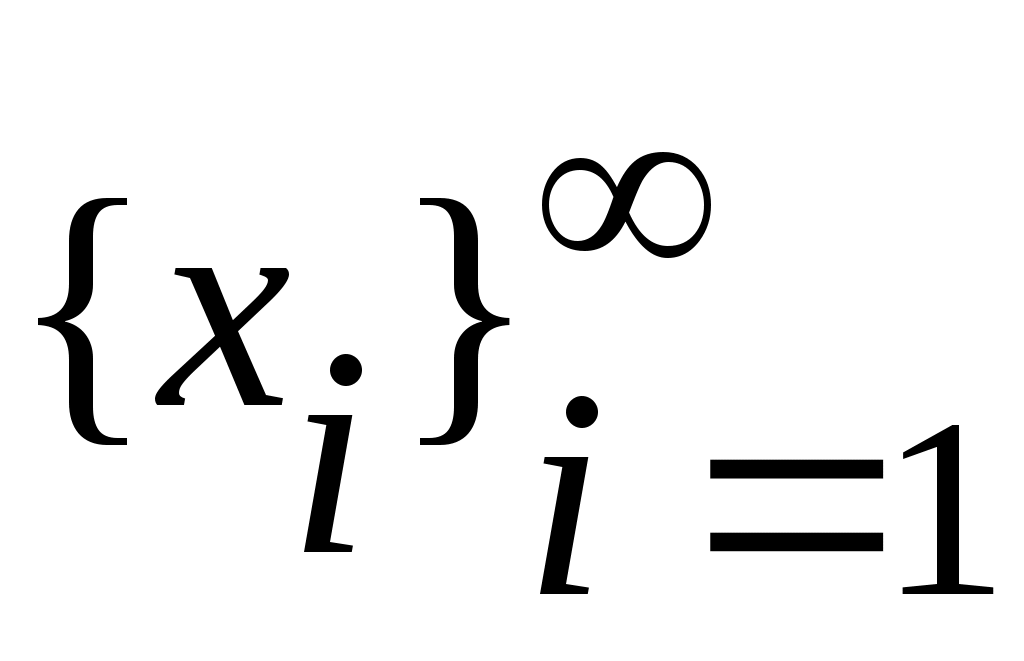 тізбегінің шегі тізбегінің шегі 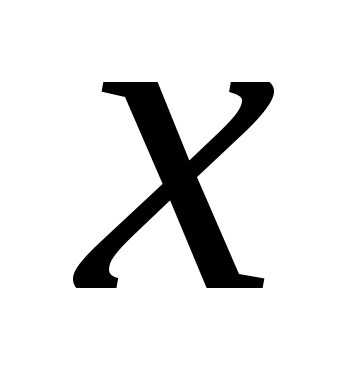 нүктесі болады; нүктесі болады;
2 – жағдай: Егер 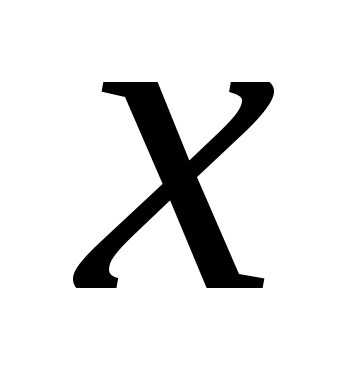 нүктесі нүктесі  жиынында жатпайтын болса, онда жиынында жатпайтын болса, онда 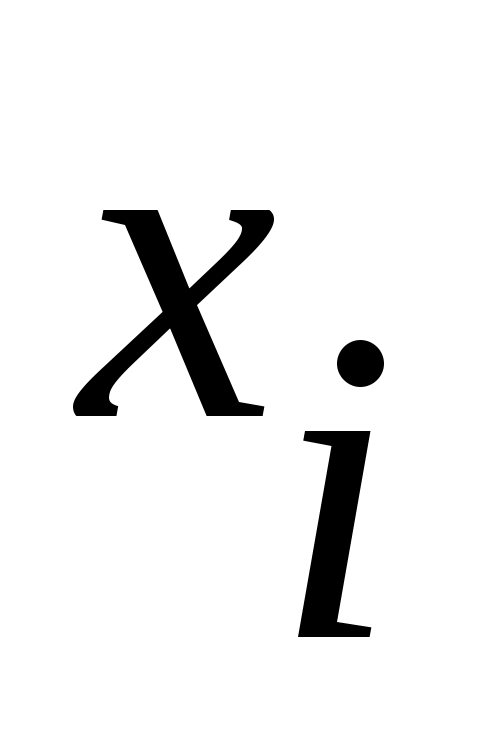 мүшесі мүшесі 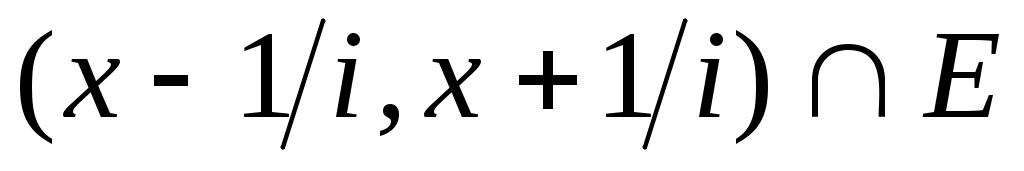 жиынында жататын жиынында жататын 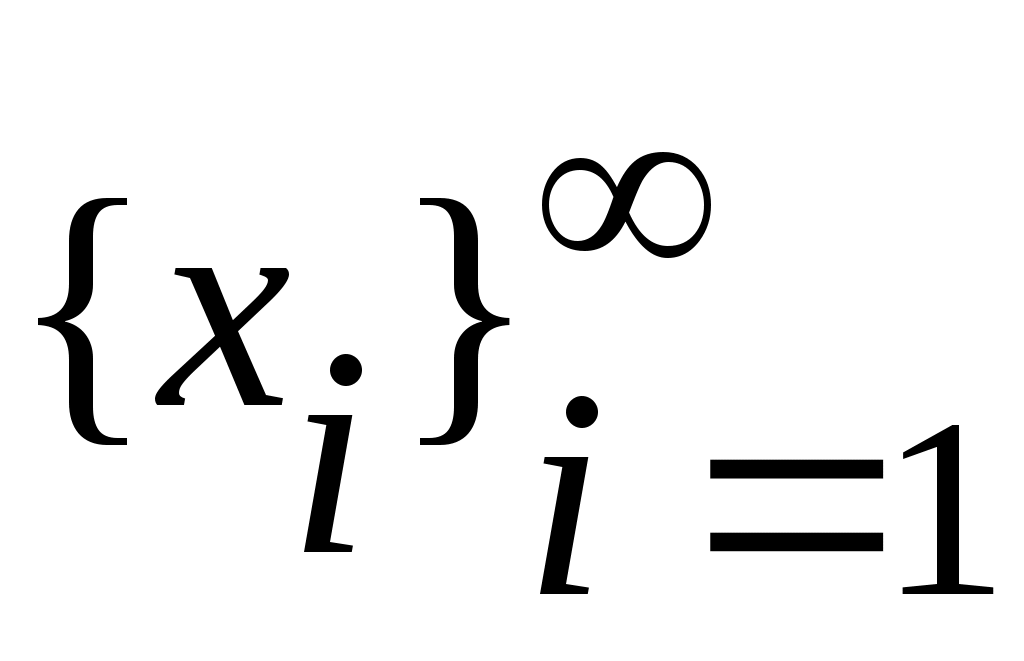 тізбегі үшін тізбегі үшін 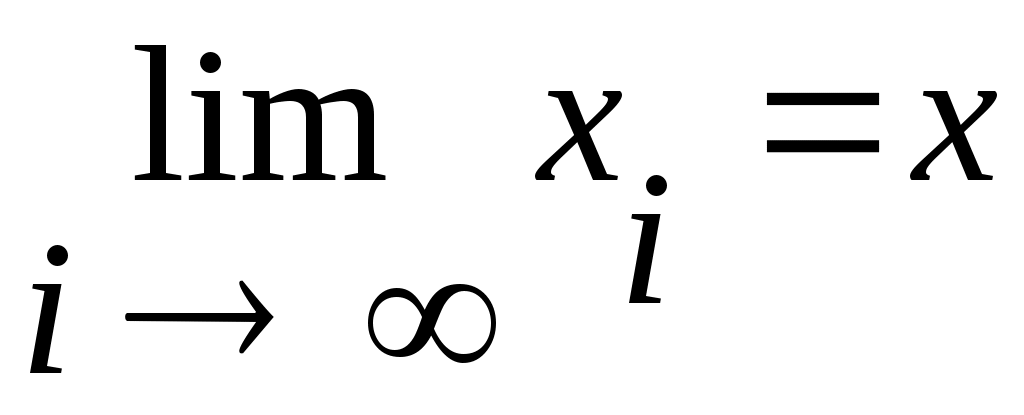 теңдігі орындалады. теңдігі орындалады.
3 – анықтама.  жиынының шектік нүктелерінің жиыны « жиынының шектік нүктелерінің жиыны « жиынының туынды жиыны» деп аталады және жиынының туынды жиыны» деп аталады және 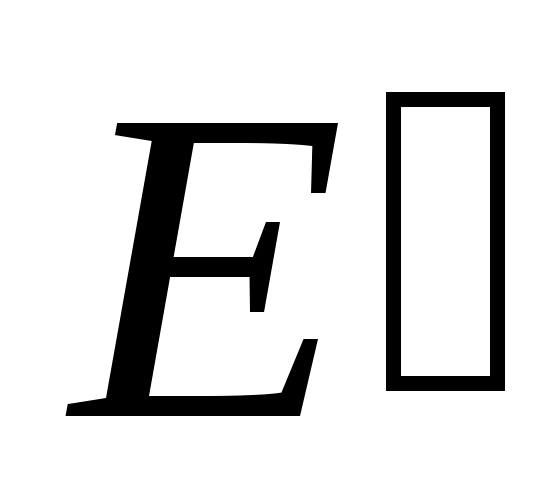 символы арқылы белгіленеді. символы арқылы белгіленеді.
3 – теорема. Егер 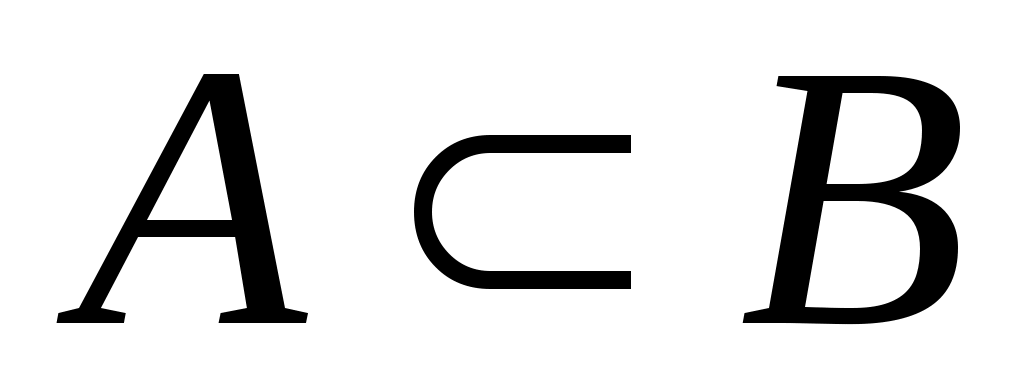 болса, онда болса, онда 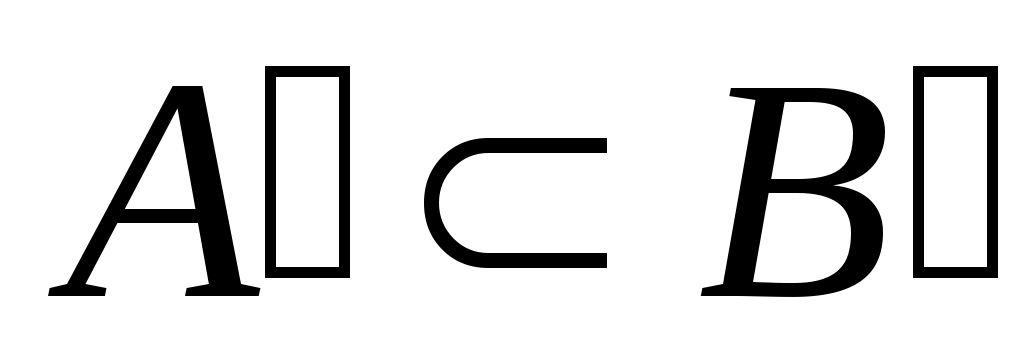 . .
Дәлелдеуі. Әрбір  нүктесінің кез келген нүктесінің кез келген 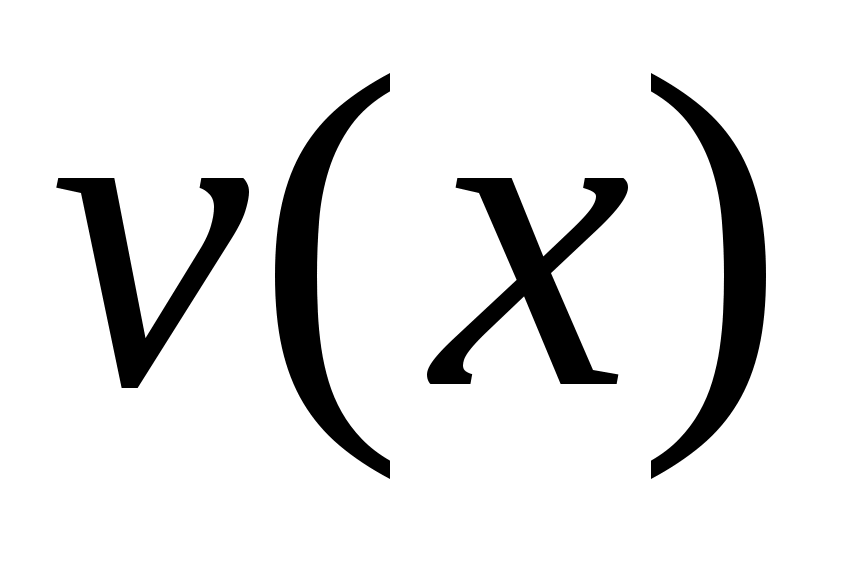 маңайының маңайының 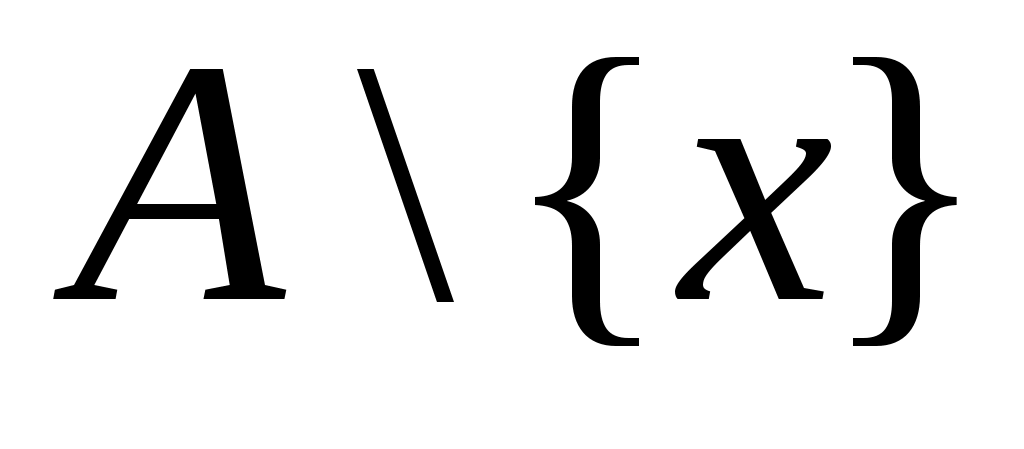 жиынымен қиылысуы бос жиын болмайтындықтан жиынымен қиылысуы бос жиын болмайтындықтан 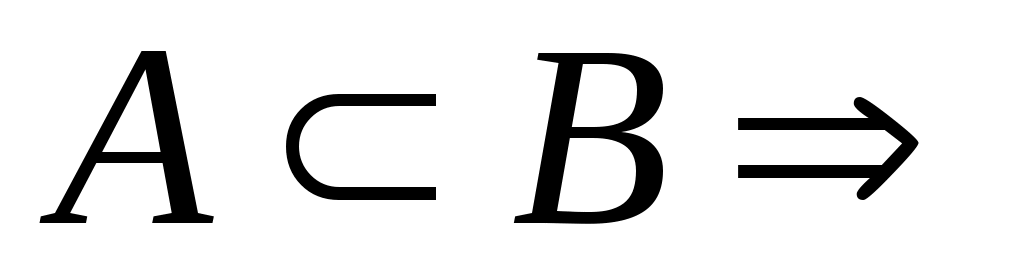
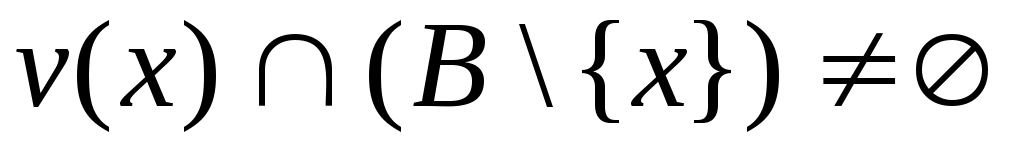 . Ендеше, . Ендеше, 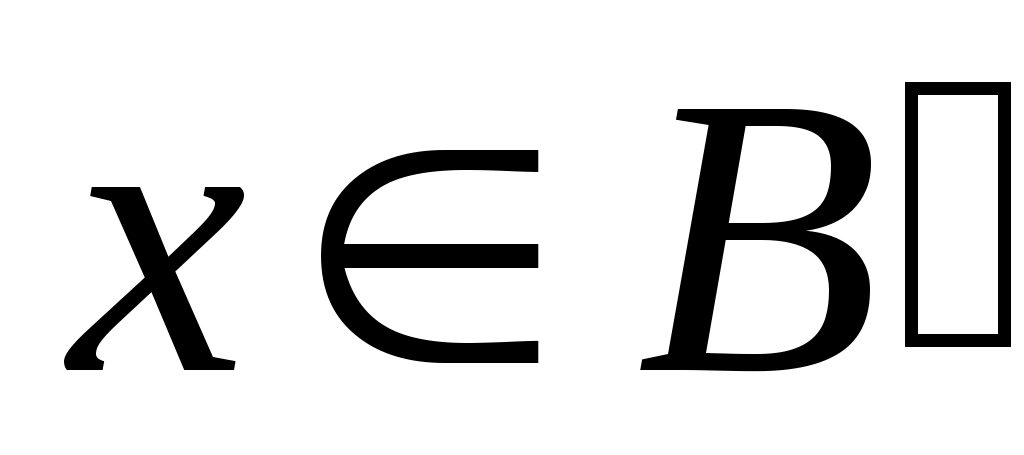 . .
4 – теорема. Әрбір 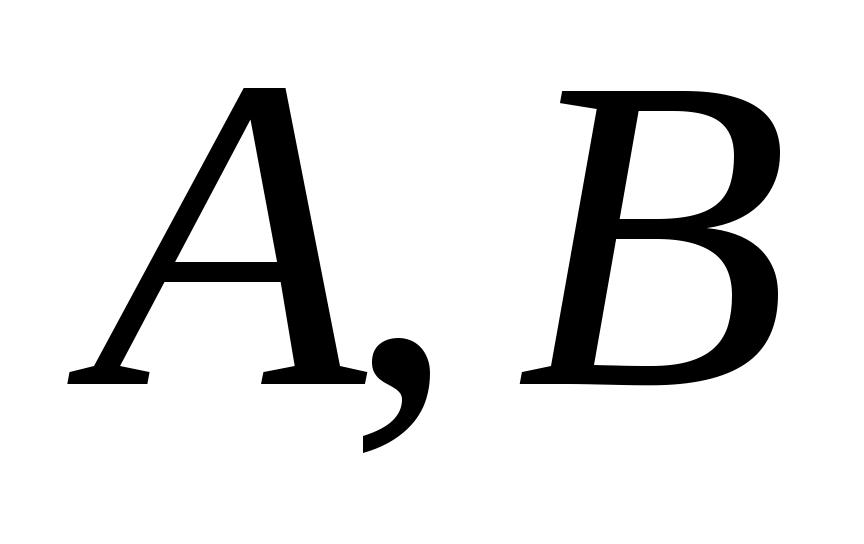 жиындары үшін жиындары үшін 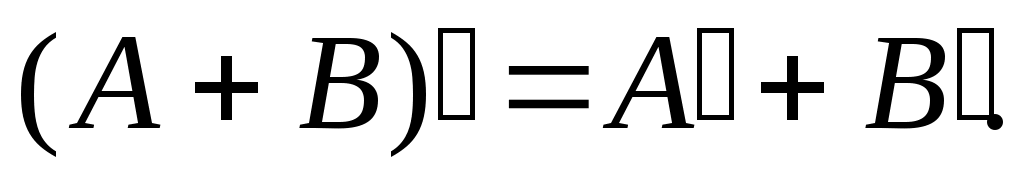
Дәлелдеуі. 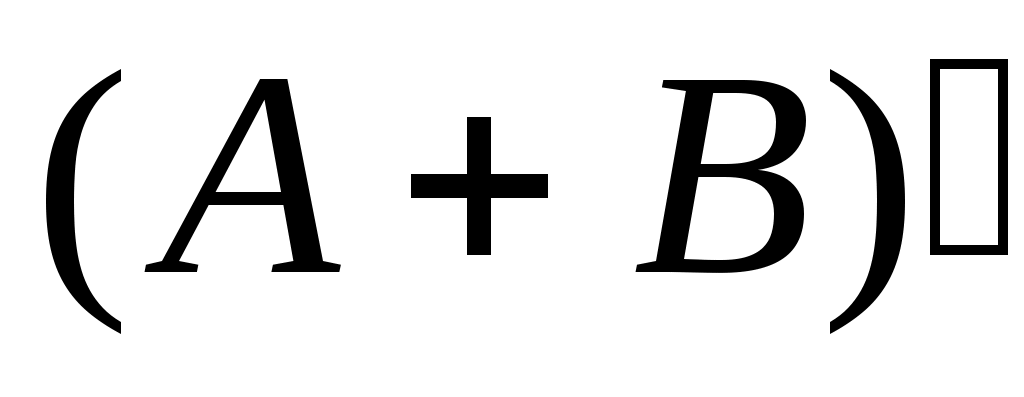 жиынының жиынының 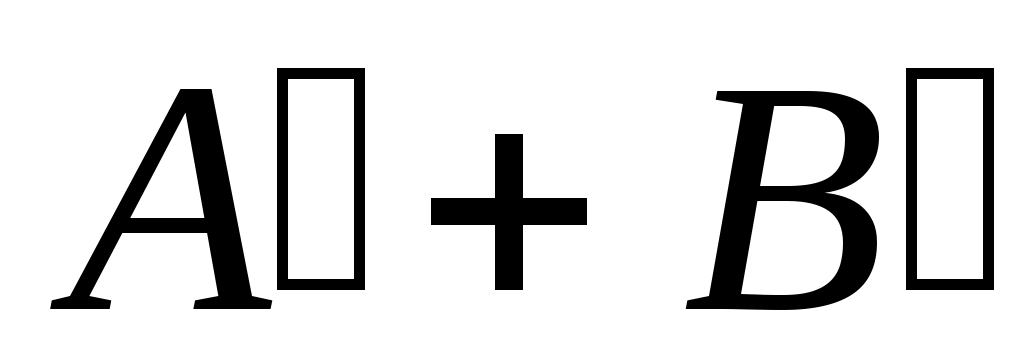 жиынымен қамтылатынын тексерсек болғаны, өйткені жиынымен қамтылатынын тексерсек болғаны, өйткені 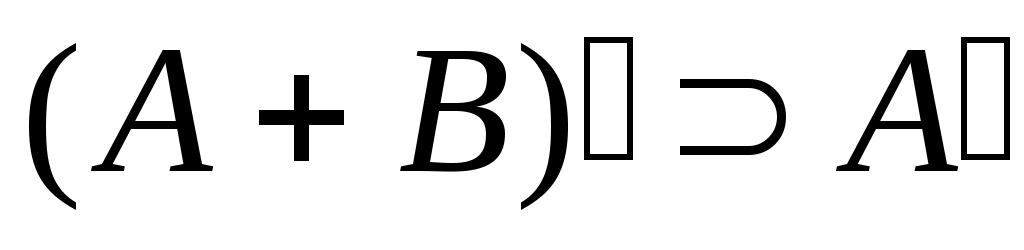 , , 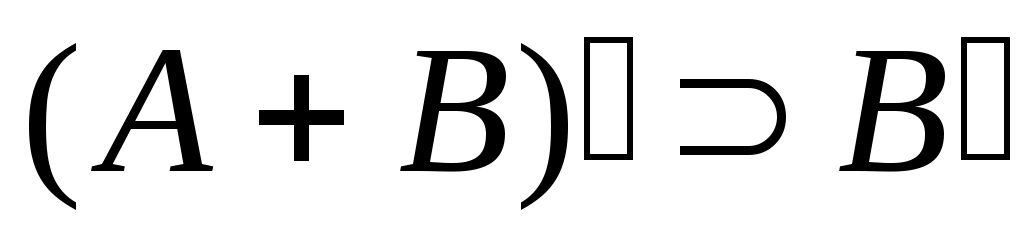 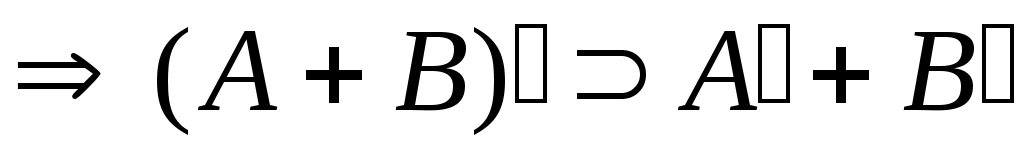 . Кері жорып, қайсыбір . Кері жорып, қайсыбір 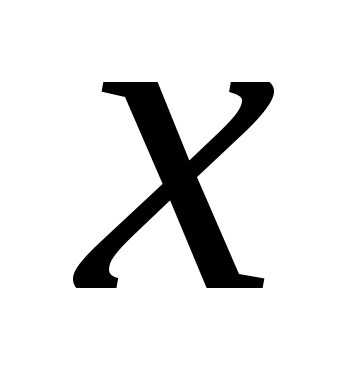 нүктесі нүктесі 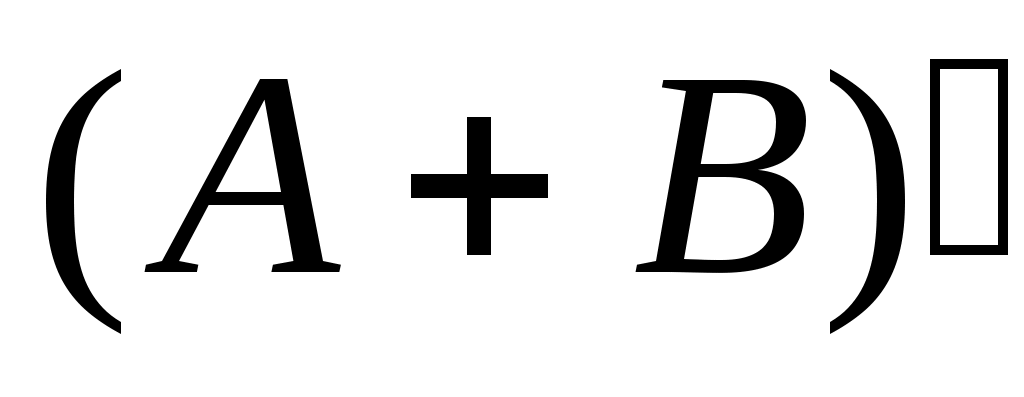 жиынында жатып, жиынында жатып, 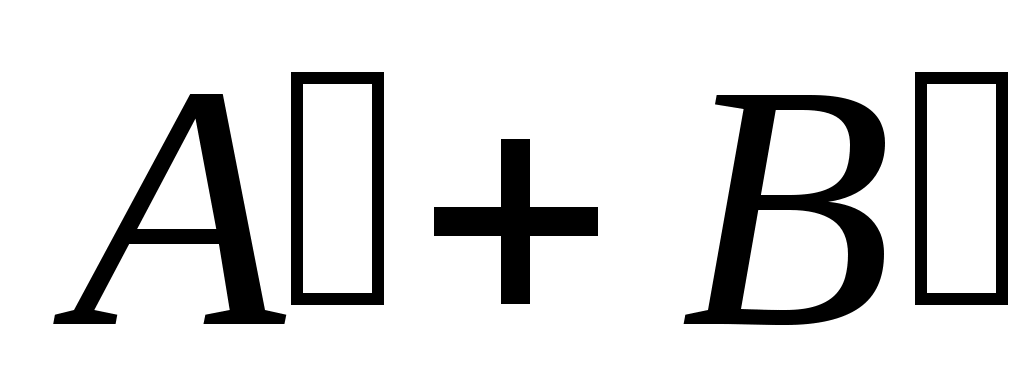 жиынында жатпайды дейік. Ал жиынында жатпайды дейік. Ал 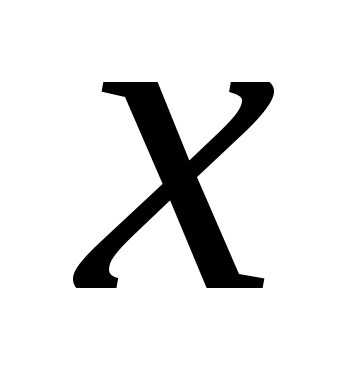 нүктесі нүктесі 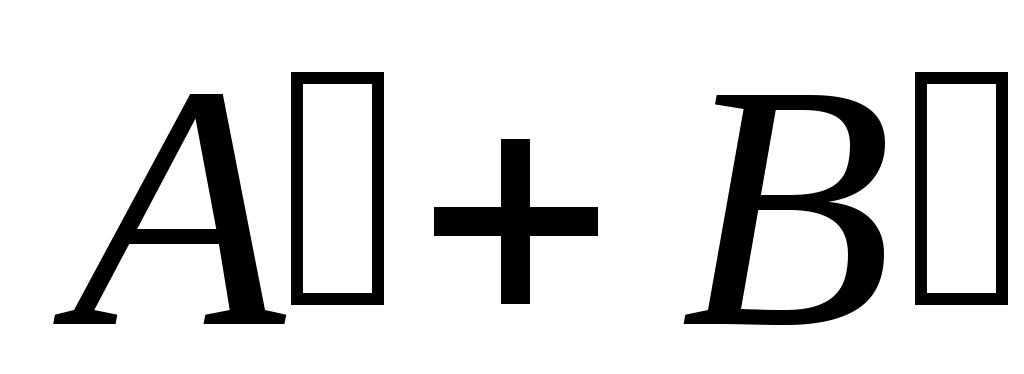 жиынында жатпаса, жиынында жатпаса,  жиынында да, жиынында да, 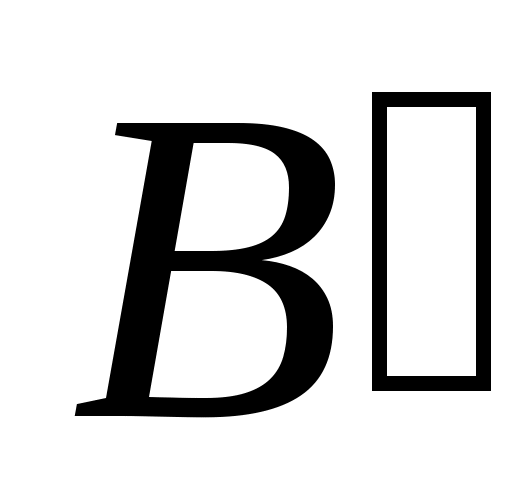 жиынында да жатпас еді. Демек, қайсыбір жиынында да жатпас еді. Демек, қайсыбір 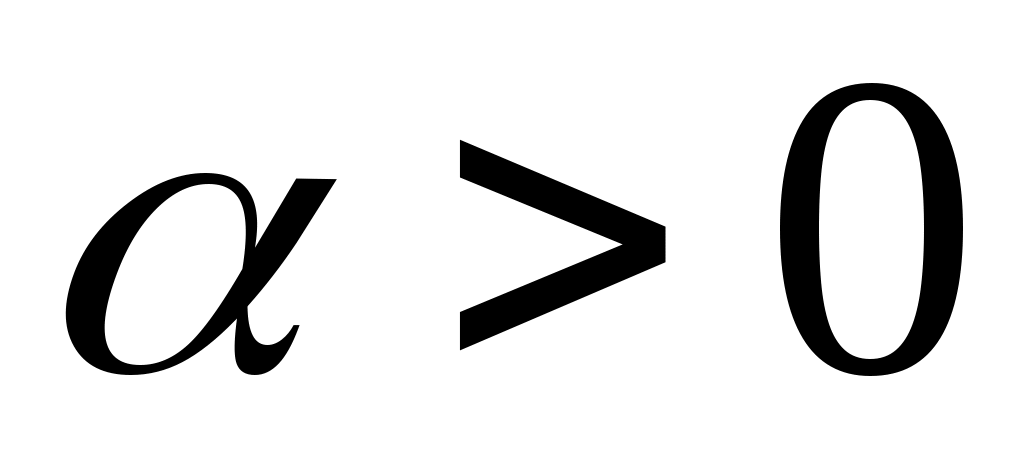 және және 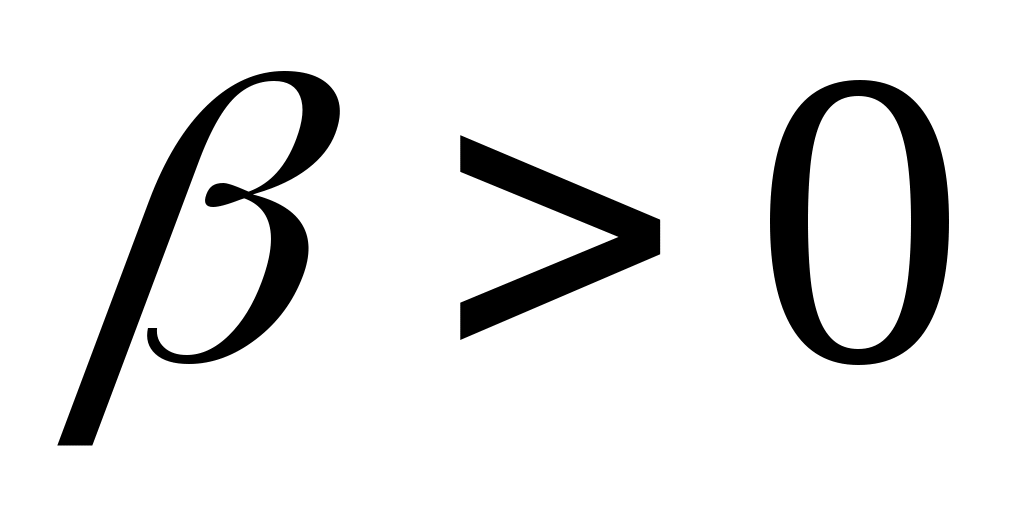 сандары үшін сәйкесінше сандары үшін сәйкесінше 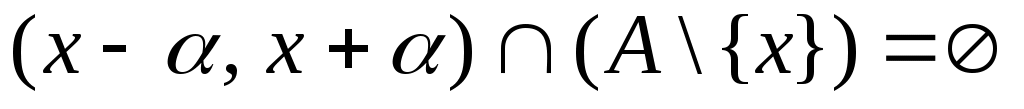 және және 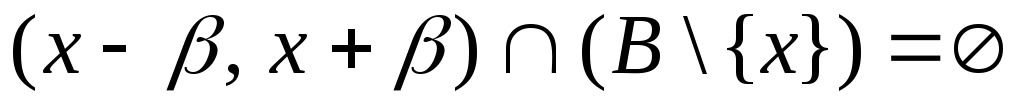 теңдіктері орындалады. Ендеше, теңдіктері орындалады. Ендеше, 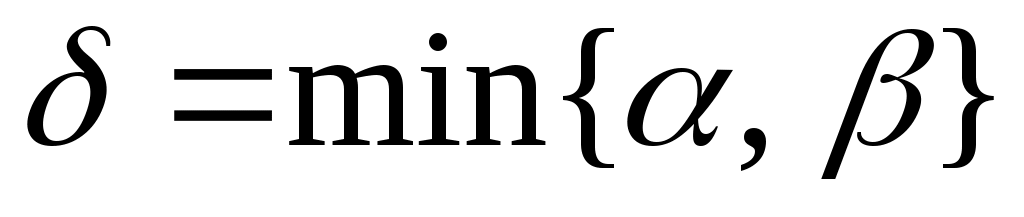 санынасәйкес санынасәйкес 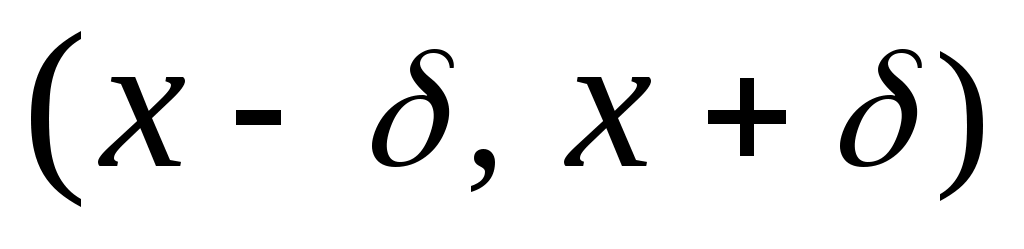 интервалының интервалының 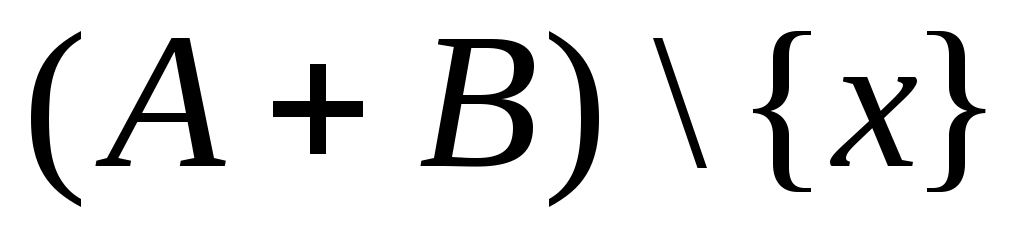 жиынымен қиылысуы бос жиын болады. Ал бұл тұжырым жиынымен қиылысуы бос жиын болады. Ал бұл тұжырым 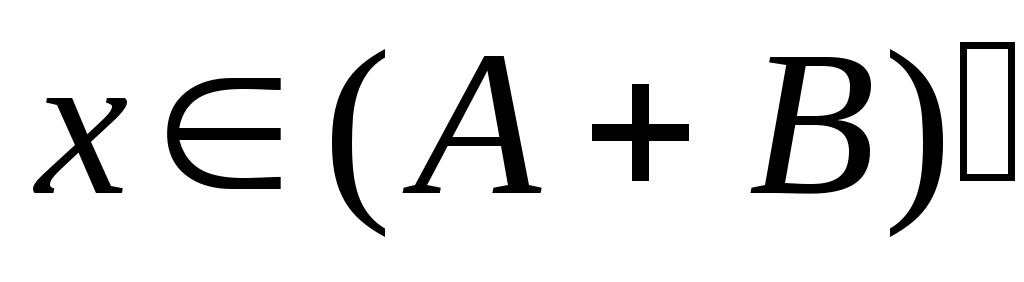 кірістіруіне қайшы. Демек, кірістіруіне қайшы. Демек, 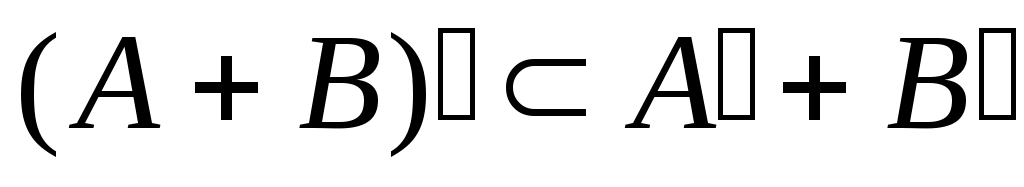 . .
4 – анықтама.  жиыны берілсін. Егер жиыны берілсін. Егер 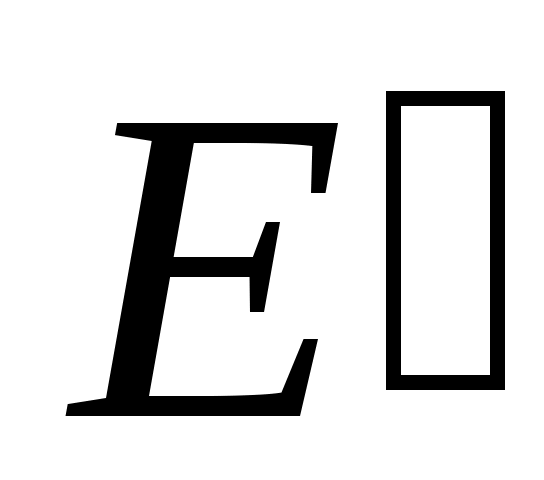 жиыны жиыны  жиынымен қамтылатын болса, онда жиынымен қамтылатын болса, онда  жиыны тұйық жиын деп аталады. жиыны тұйық жиын деп аталады.
Тұйық жиындардың мысалдарын келтірейік.1) 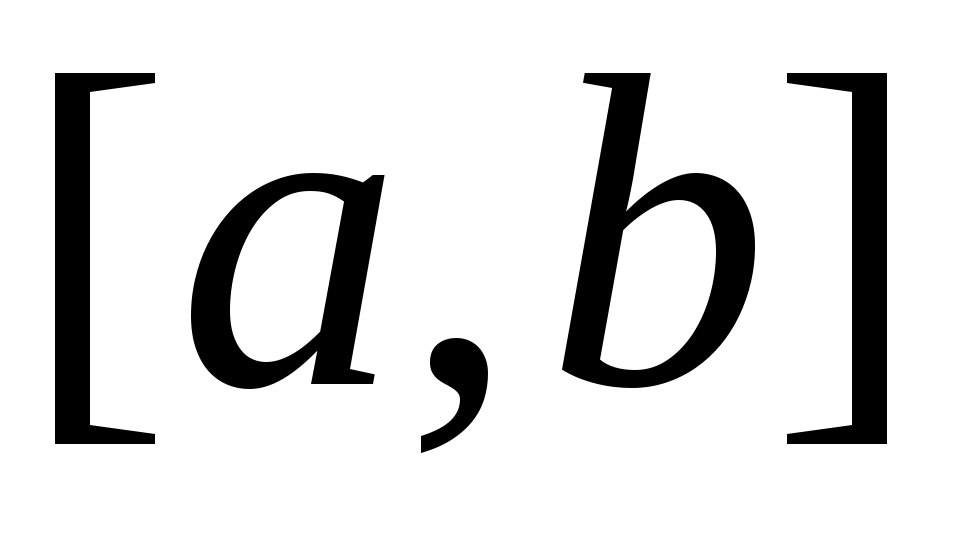 сегменті, сегменті, 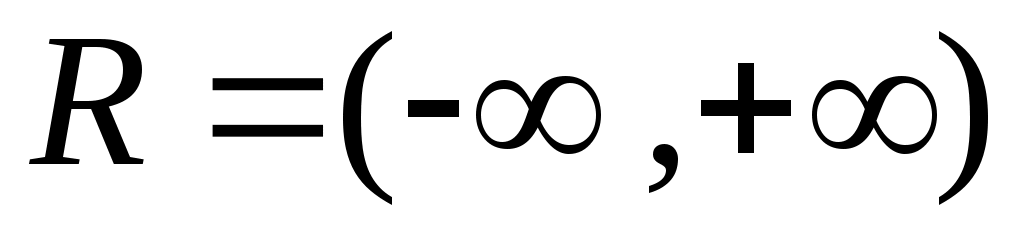 жиыны, кез келген ақырлы жиын – тұйық жиындар; 2) Әрбір жиыны, кез келген ақырлы жиын – тұйық жиындар; 2) Әрбір  үшін үшін 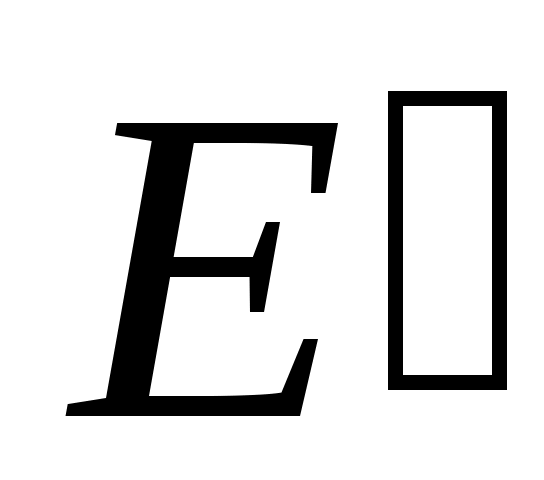 жиыны – тұйық жиын; жиыны – тұйық жиын;
3) Әрбір  үшін үшін 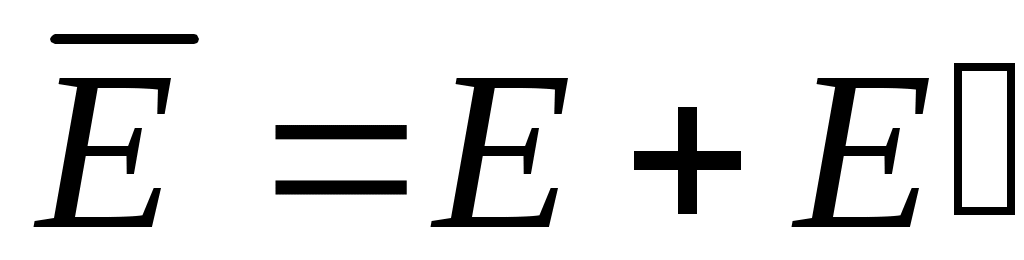 жиыны ( жиыны ( жиынының тұйықталуы) – тұйық жиын, өйткені, жиынының тұйықталуы) – тұйық жиын, өйткені, 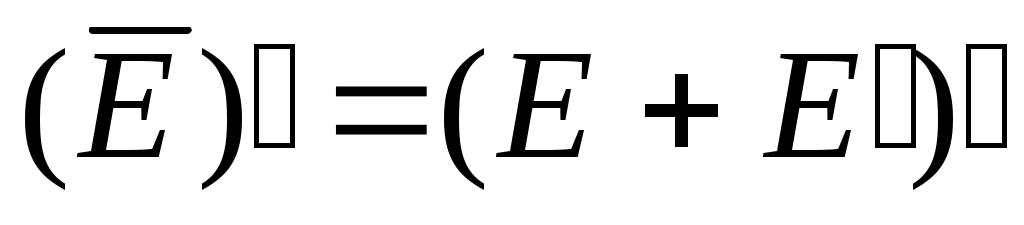 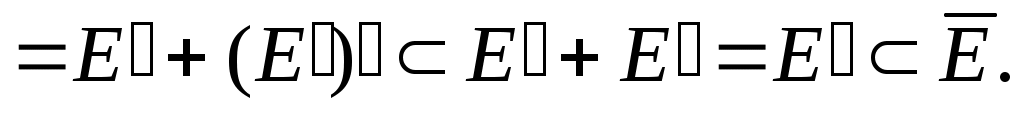
4) Тұйық жиынның тағы бір мысалы – Кантор жиыны. Бұл жиын 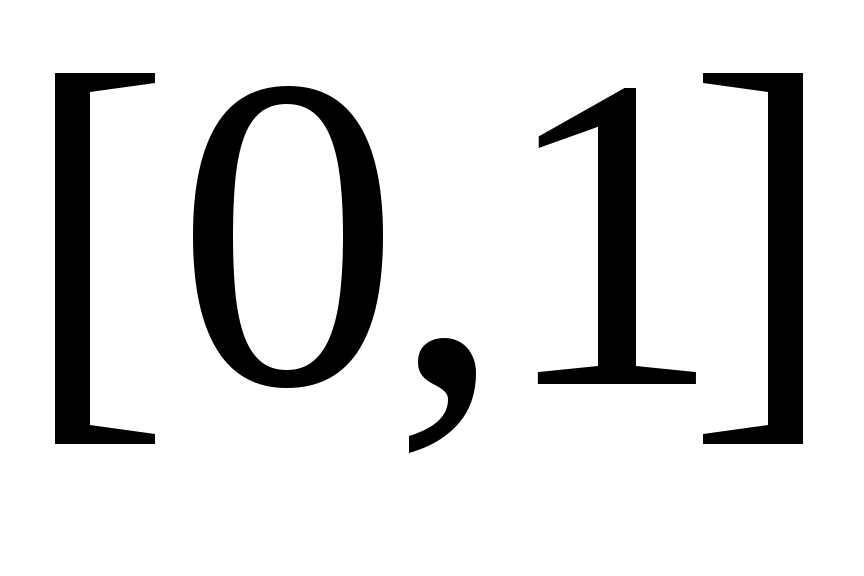 сегментінен өзара қиылыспайтын сегментінен өзара қиылыспайтын 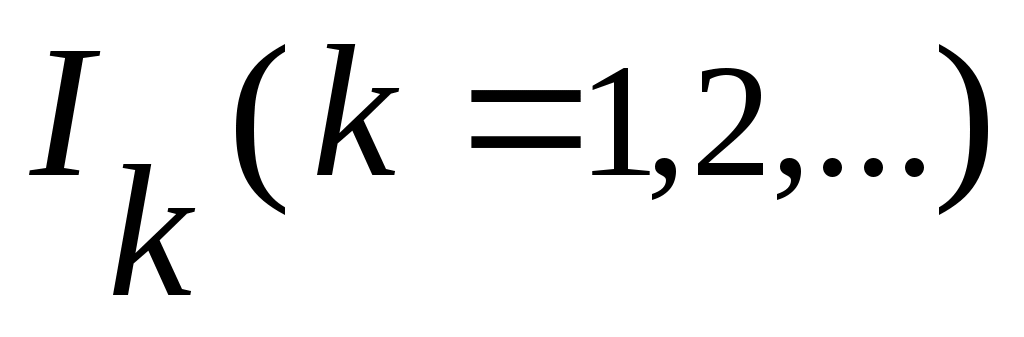 интервалдарын алып тастау арқылы алынады. Сонымен, Кантор жиыны – интервалдарын алып тастау арқылы алынады. Сонымен, Кантор жиыны – 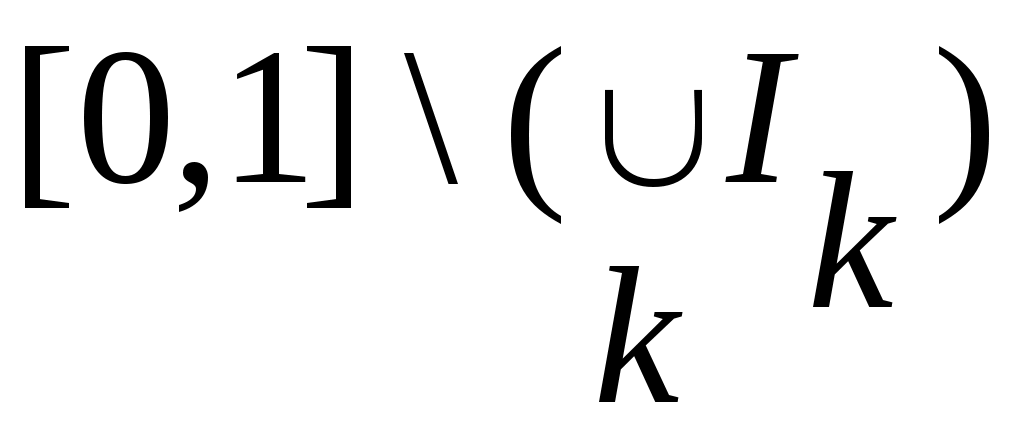 жиыны. жиыны. 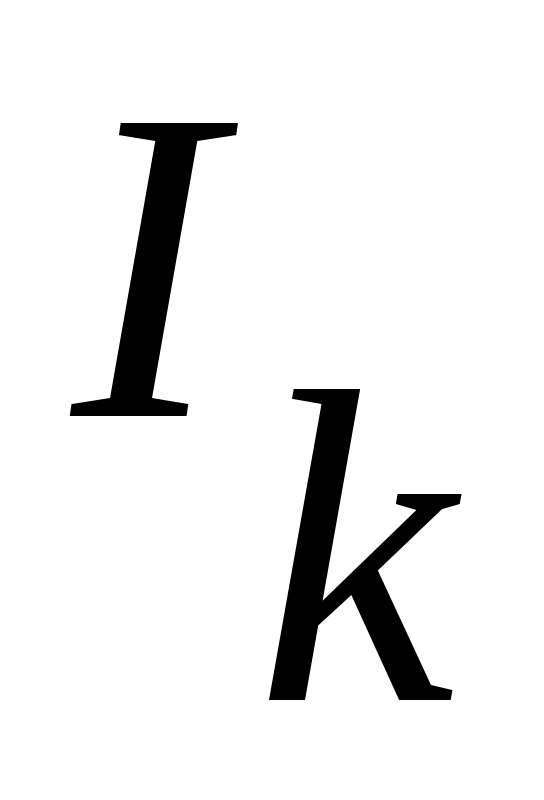 интервалдары былай анықталады: 1– ші қадамда интервалдары былай анықталады: 1– ші қадамда 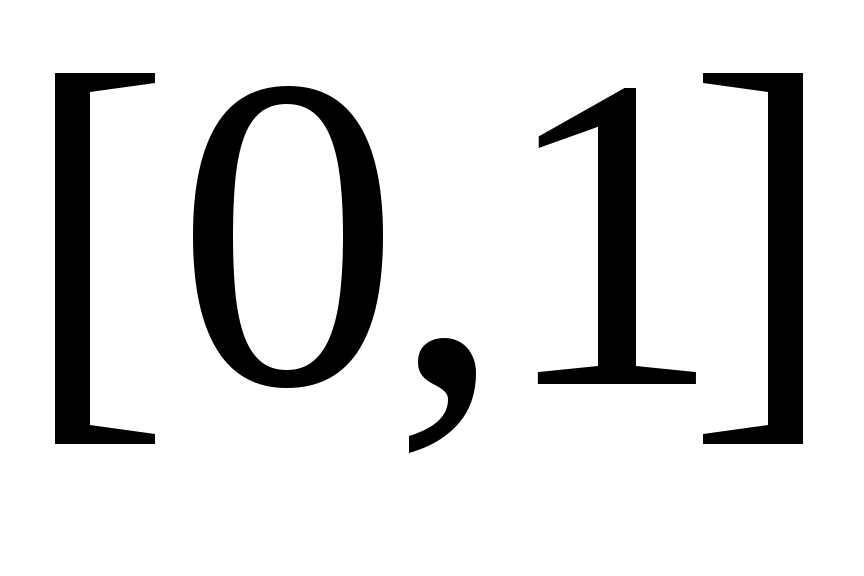 сегментін ұзындықтары тең үш интервалға бөліп, сегментін ұзындықтары тең үш интервалға бөліп, 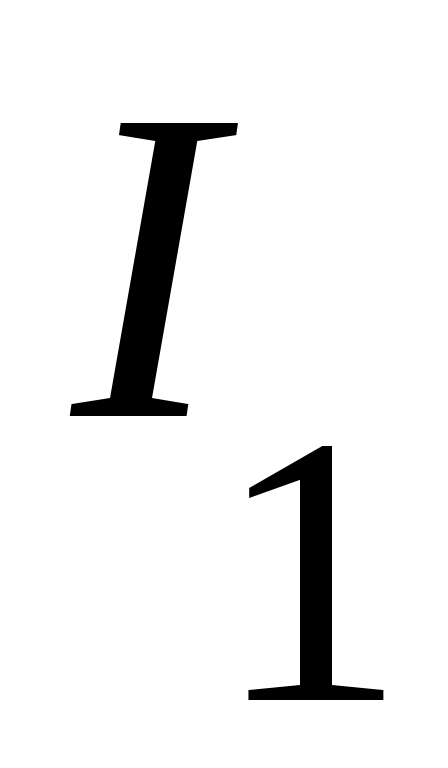 арқылы ортаңғы арқылы ортаңғы 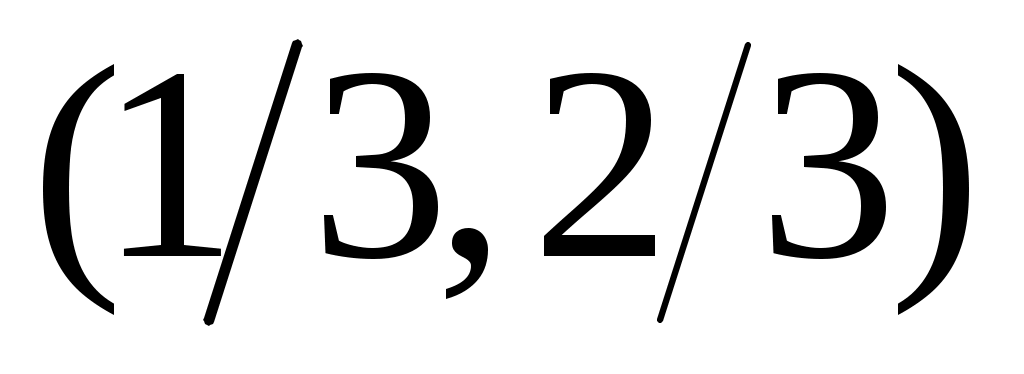 интервалын белгілейміз. 2 – ші қадамда интервалын белгілейміз. 2 – ші қадамда 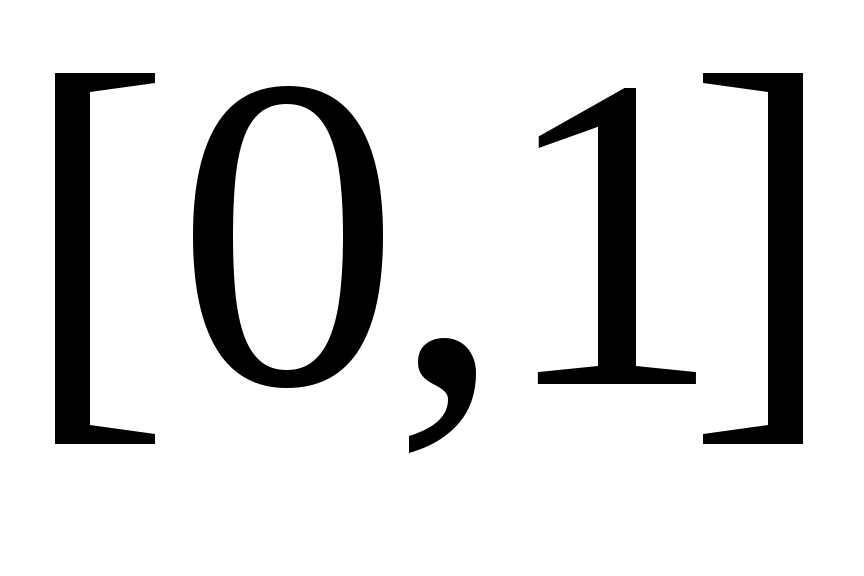 сегментінде қалған сегментінде қалған 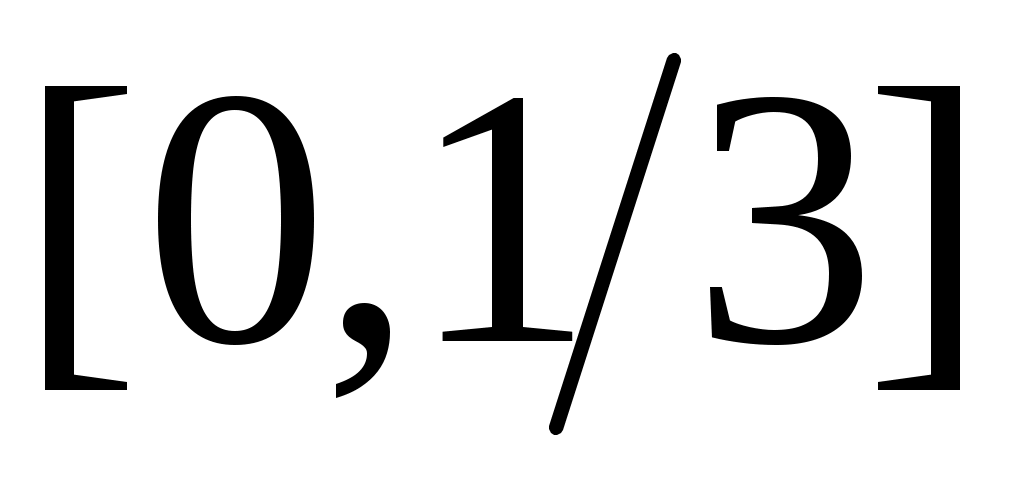 және және 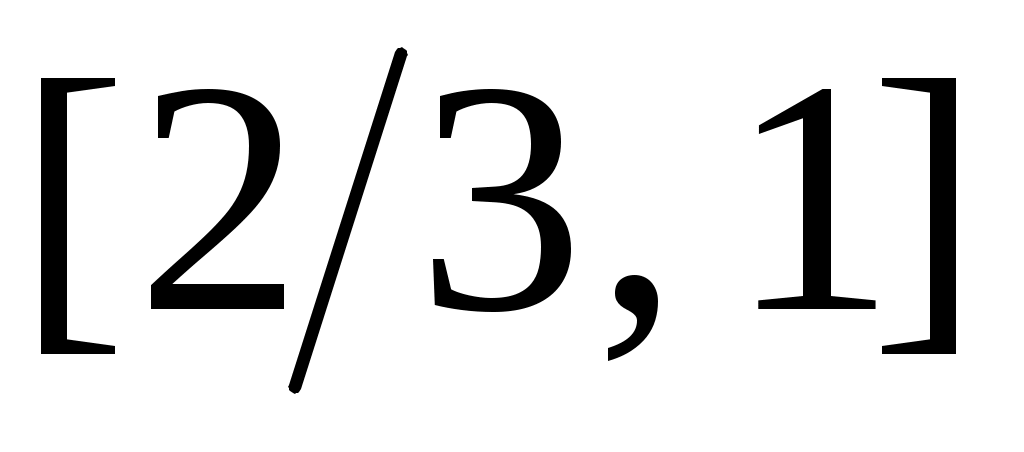 сегменттерінің әрқайсысын ұзындықтары тең үш интервалға бөліп, ортаңғы сегменттерінің әрқайсысын ұзындықтары тең үш интервалға бөліп, ортаңғы 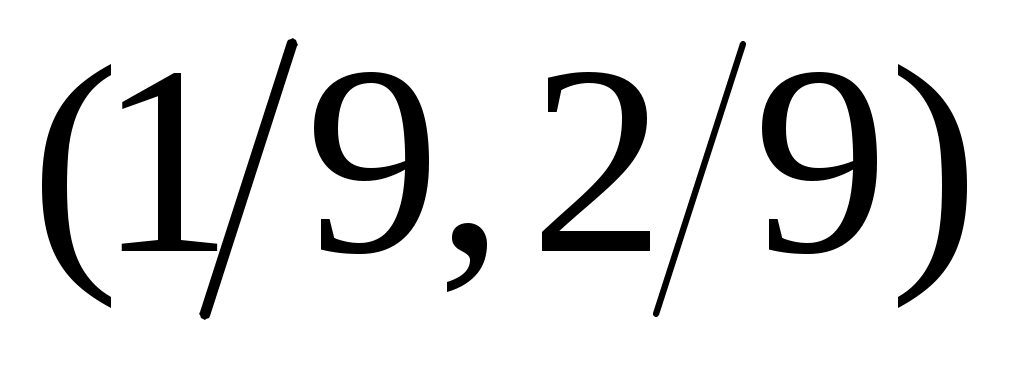 және және 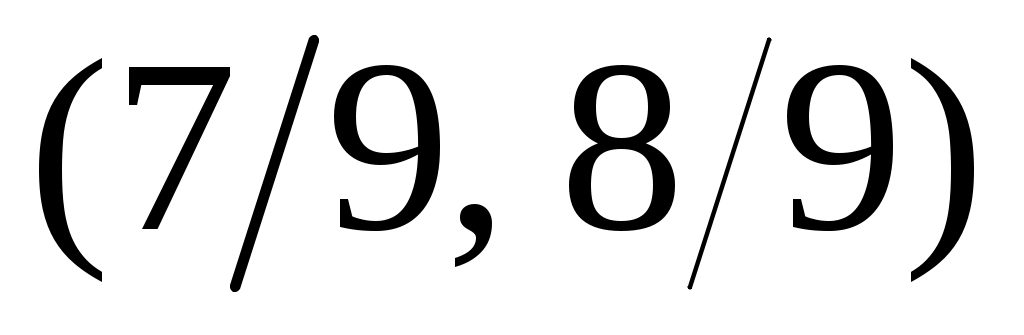 интервалдарын интервалдарын 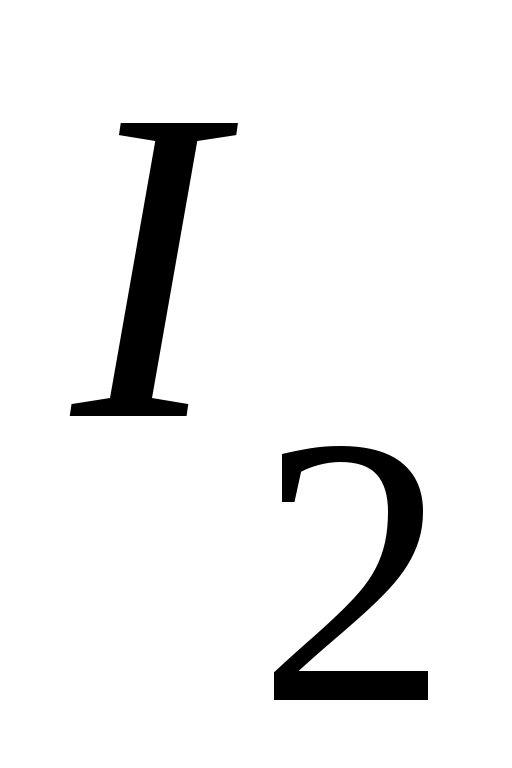 және және 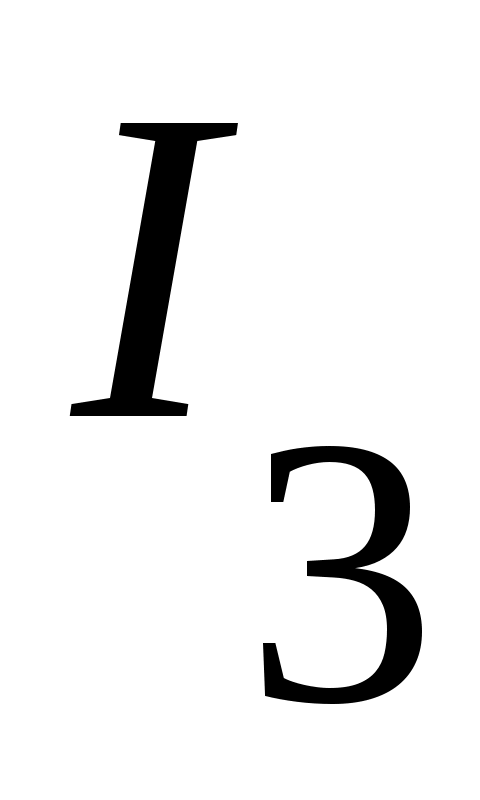 арқылы белгілейміз. 3 – ші қадамда алдыңғы екі қадамда жасалған әрекеттерді қайталасақ, арқылы белгілейміз. 3 – ші қадамда алдыңғы екі қадамда жасалған әрекеттерді қайталасақ,
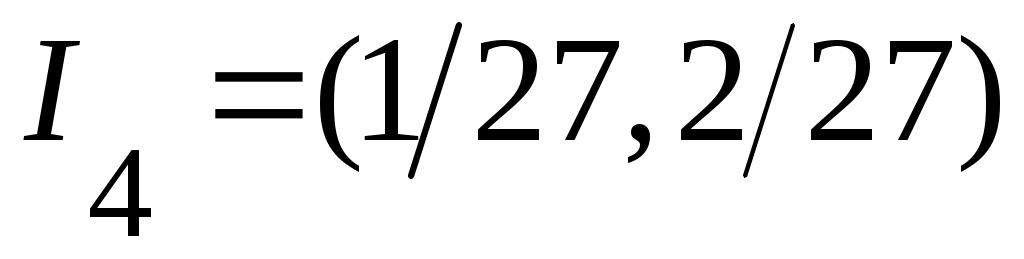 , ,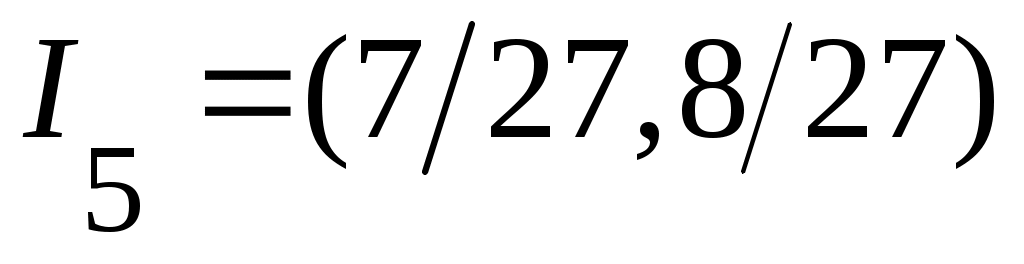 , ,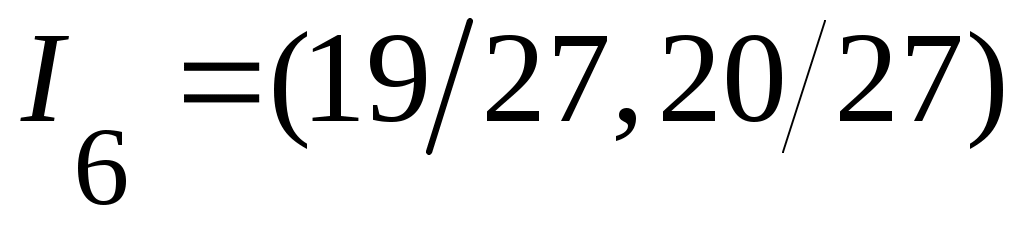 , ,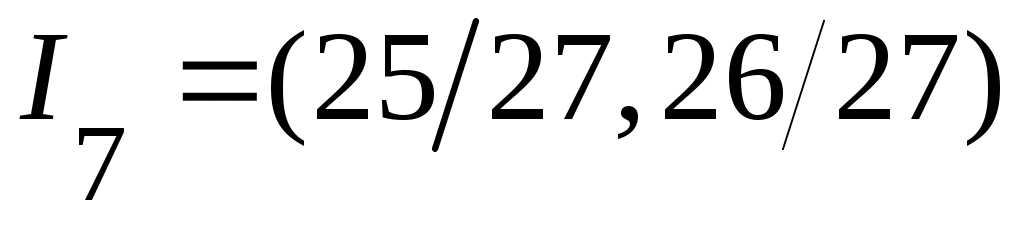 интервалдарын аламыз. Осылай жалғастыра берсек, әрбір мүшесі интервал болатын интервалдарын аламыз. Осылай жалғастыра берсек, әрбір мүшесі интервал болатын 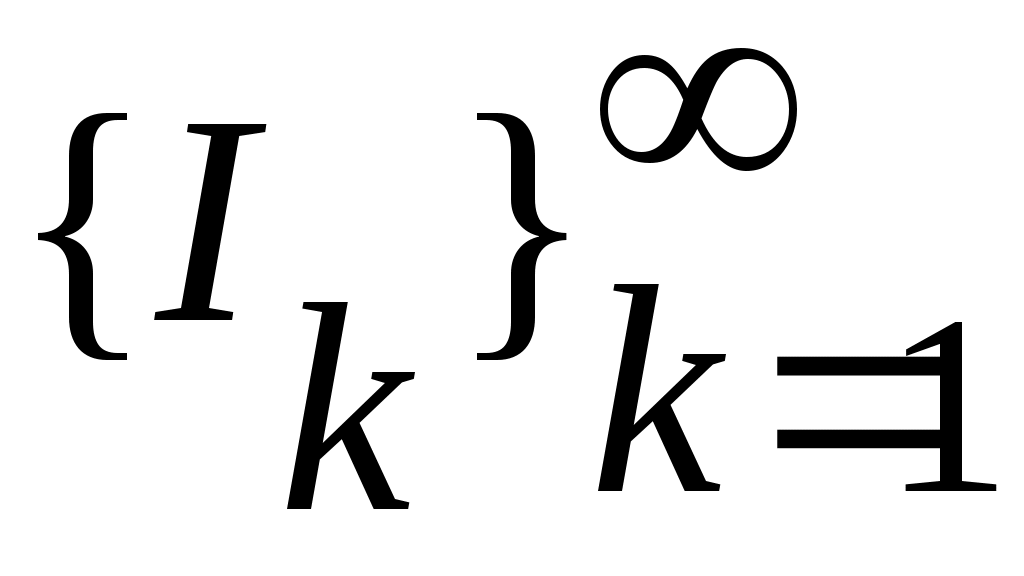 тізбегіне келеміз. тізбегіне келеміз.
5 – анықтама. 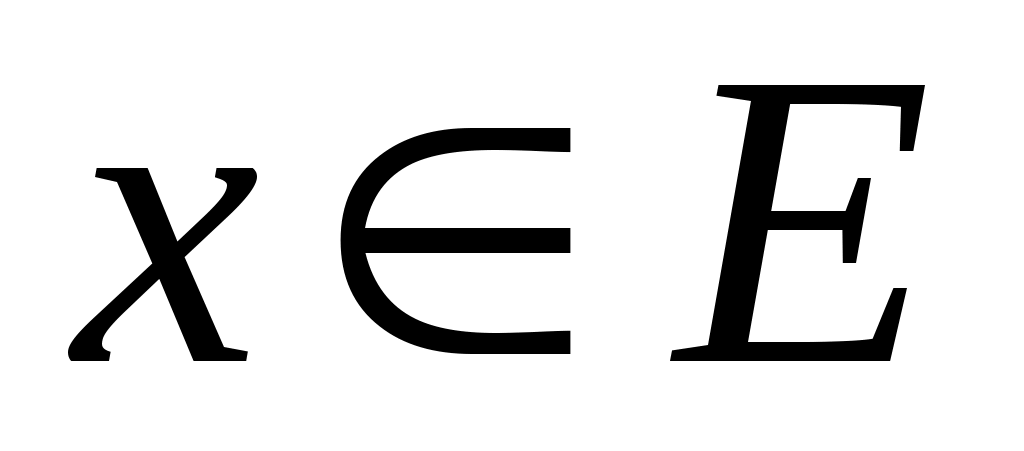 нүктесі берілсін. Егер нүктесі берілсін. Егер 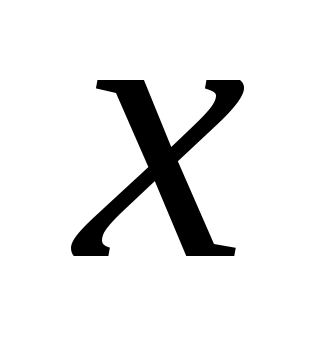 нүктесінің қайсыбір маңайы нүктесінің қайсыбір маңайы 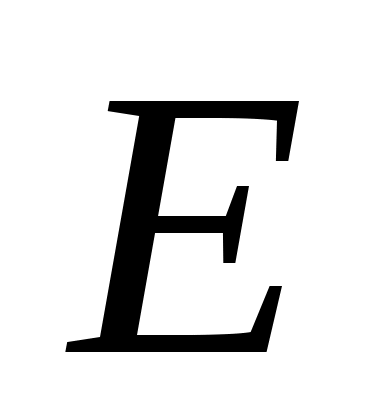 жиынымен қамтылатын болса, онда жиынымен қамтылатын болса, онда 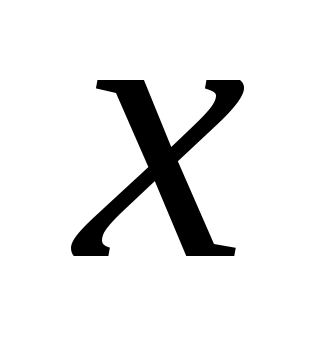 нүктесін « нүктесін «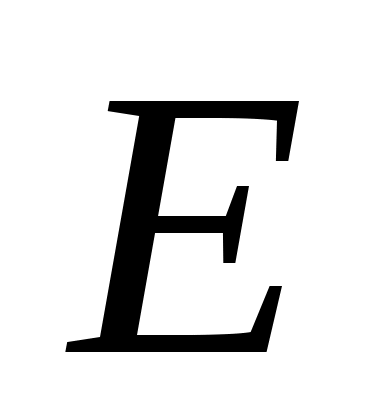 жиынының ішкі нүктесі» деп, ал әрбір нүктесі ішкі нүкте болатын жиынды ашық жиын деп атаймыз. Ашық жиындардың мысалдарын келтірейік. 1) жиынының ішкі нүктесі» деп, ал әрбір нүктесі ішкі нүкте болатын жиынды ашық жиын деп атаймыз. Ашық жиындардың мысалдарын келтірейік. 1) 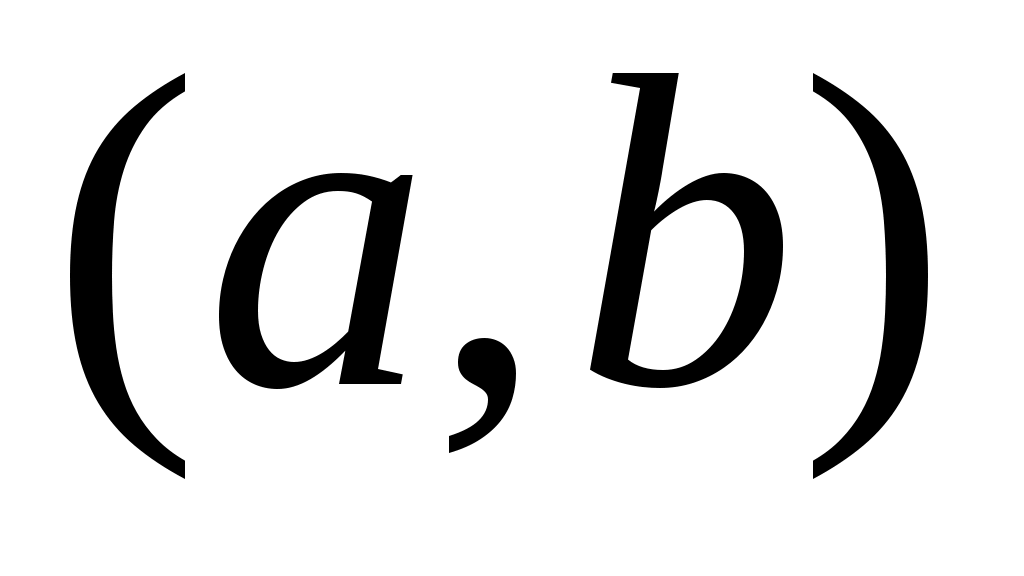 интервалы – ашық жиын, өйткені, әрбір интервалы – ашық жиын, өйткені, әрбір 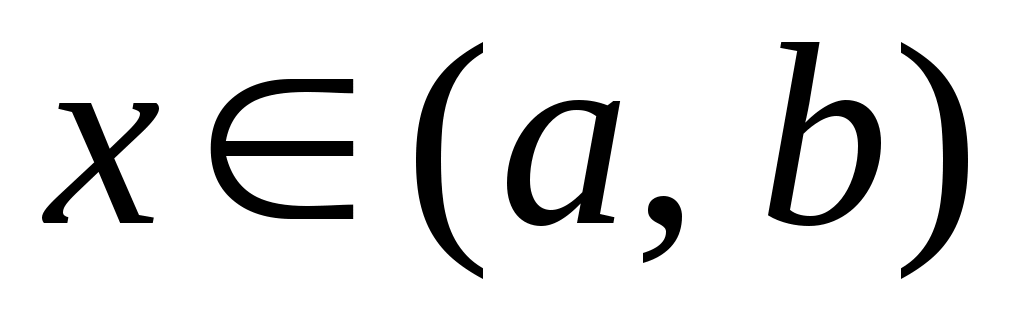 үшін үшін 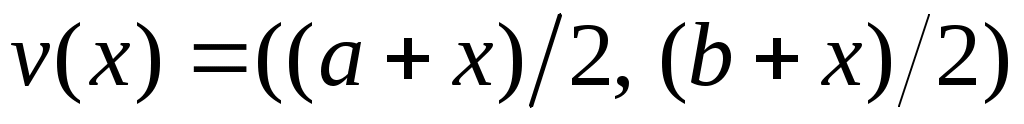 интервалы интервалы 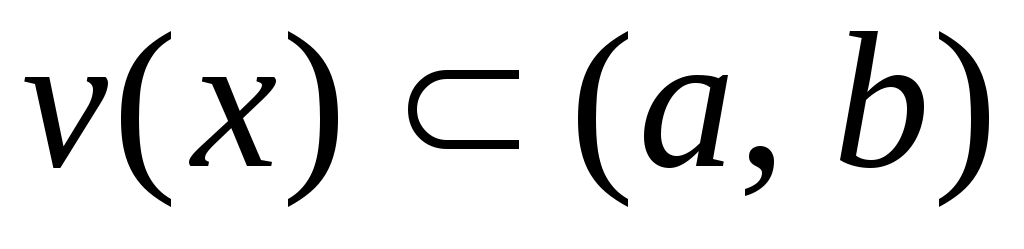 кірістіруін қанағаттандырады; 2) кірістіруін қанағаттандырады; 2) 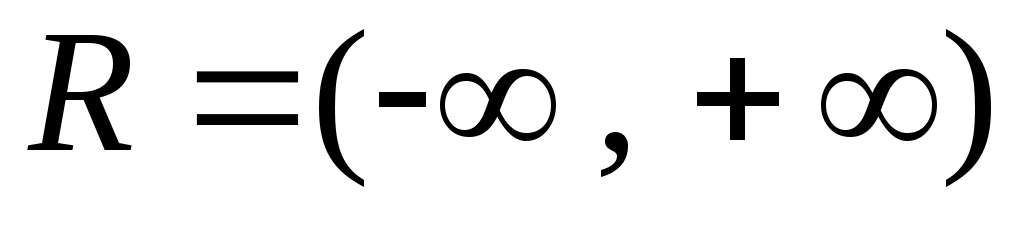 жиыны – ашық жиын. жиыны – ашық жиын.
|
|
|
 Скачать 1.5 Mb.
Скачать 1.5 Mb.