|
|
ГЛ1. 1 тарау. Жиындар теориясыны элементтері жиыны жиыныны жиыншасы болан жадайда жиыны жиынын амтиды
1 – ТАРАУ. ЖИЫНДАР ТЕОРИЯСЫНЫҢ ЭЛЕМЕНТТЕРІ
 жиыны жиыны 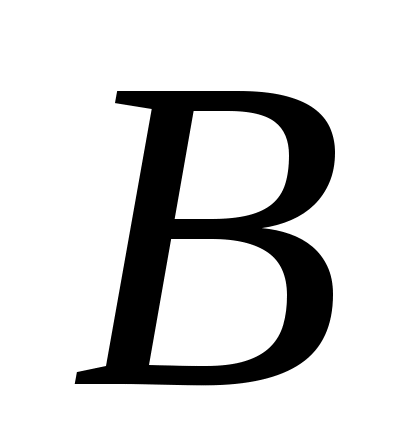 жиынының жиыншасы болған жағдайда « жиынының жиыншасы болған жағдайда «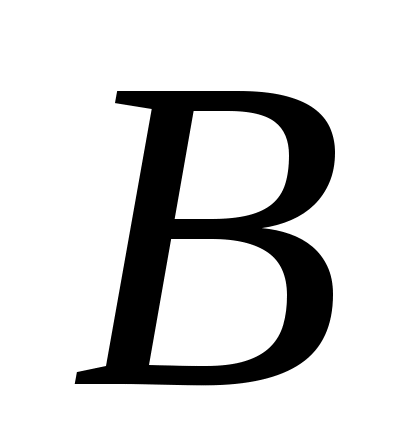 жиыны жиыны  жиынын қамтиды» немесе « жиынын қамтиды» немесе « жиыны жиыны 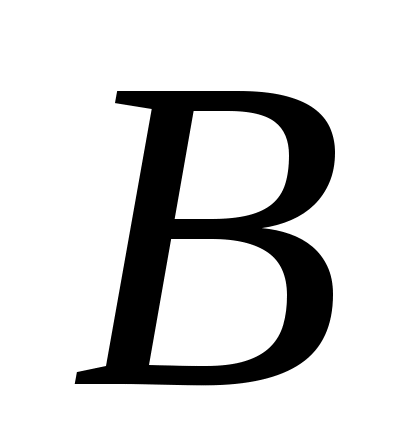 жиынымен қамтылады» деп айтатын боламыз. жиынымен қамтылады» деп айтатын боламыз.  жиынының толықтауыш жиынын (қысқаша: толықтауышын) жиынының толықтауыш жиынын (қысқаша: толықтауышын)  символымен белгілейміз. символымен белгілейміз.
§1. Жиынның супремумі мен инфимумі
Алдағы тарауларда жиынның супремумі мен инфимумінің қасиеттерін жиі пайдаланатын боламыз.
Жоғарыдан (Төменнен) шенелген  жиынының супремумін (инфимумін), яғни, жиынының супремумін (инфимумін), яғни,  жиынының жоғарғы (төменгі) шекараларының ең кішісін (үлкенін) жиынының жоғарғы (төменгі) шекараларының ең кішісін (үлкенін) 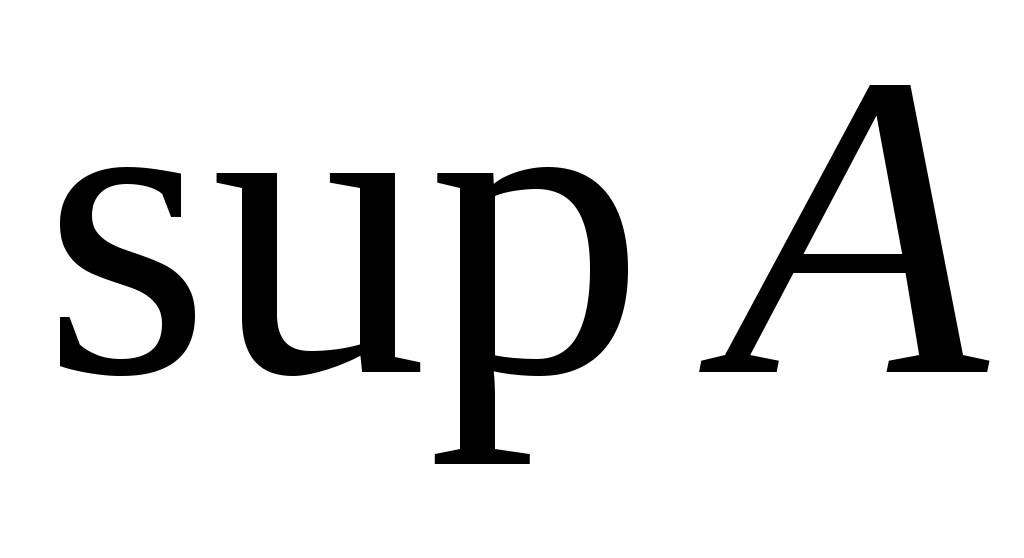 ( (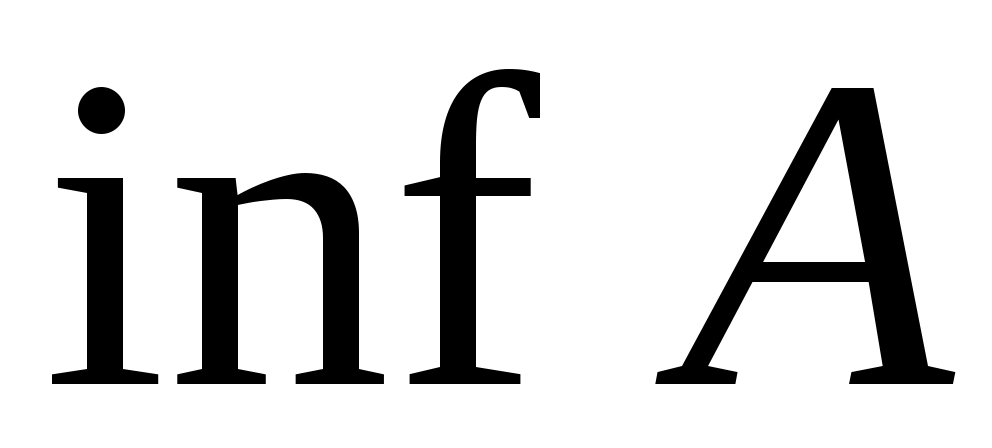 ) символымен белгілейміз. Жоғарыдан (Төменнен) шенелмеген ) символымен белгілейміз. Жоғарыдан (Төменнен) шенелмеген  жиыны үшін жиыны үшін 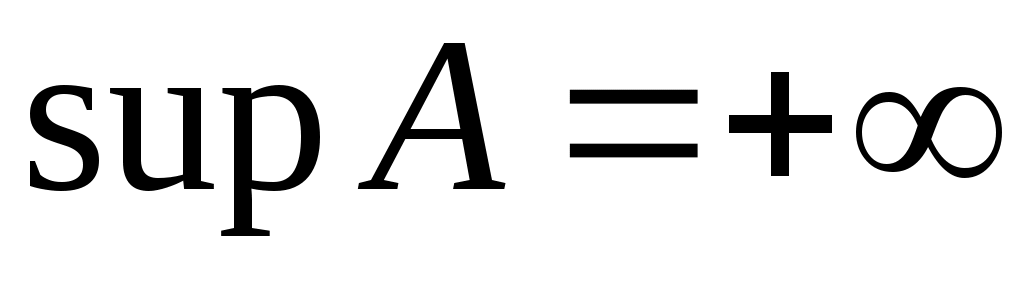 ( (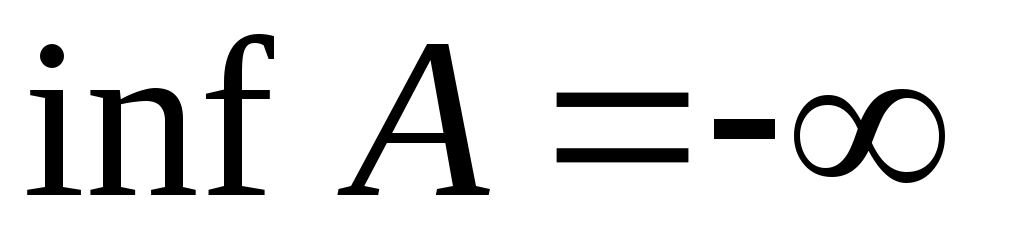 ) теңдігі жазылады. ) теңдігі жазылады.
1 – теорема. Ең үлкен (ең кіші) элементі бар  жиыны үшін жиыны үшін 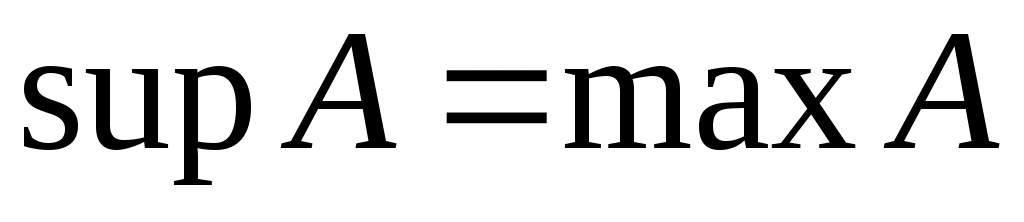 ( (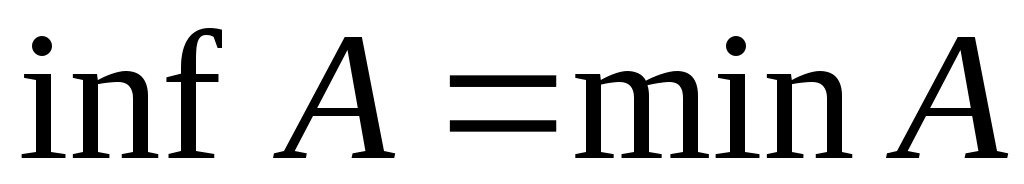 ) теңдігі орындалады. ) теңдігі орындалады.
Дәлелдеуі. 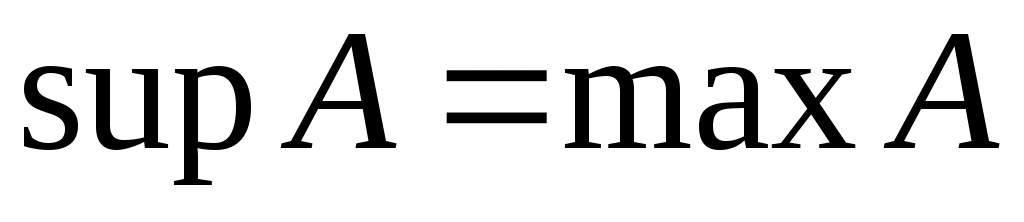 теңдігін тексерейік. Бір жағынан, теңдігін тексерейік. Бір жағынан, 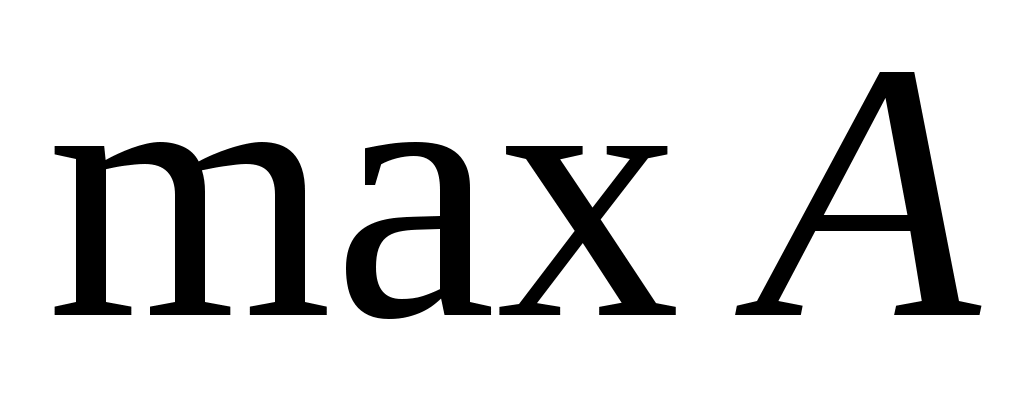 саны – саны –  жиынының жоғарғы шекарасы, ал жиынының жоғарғы шекарасы, ал 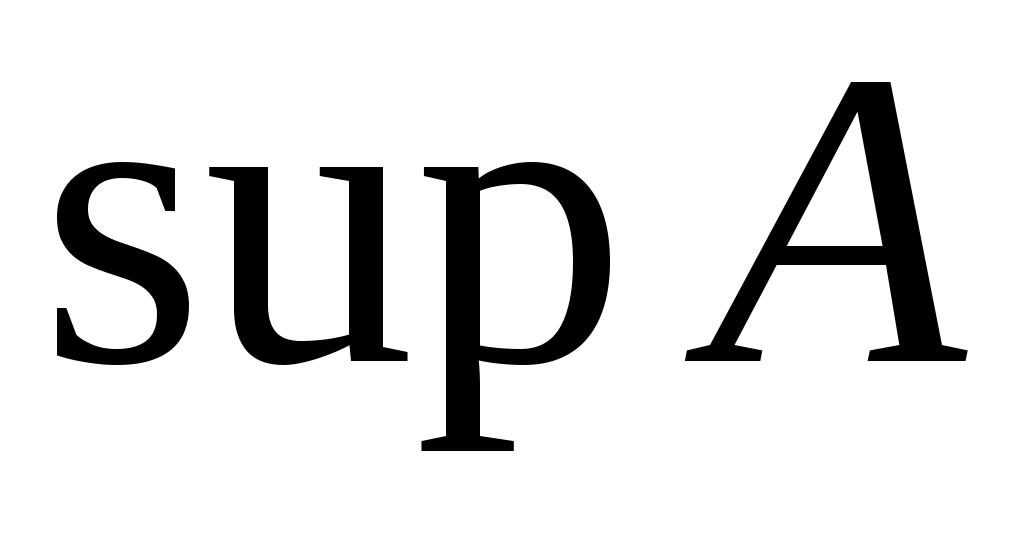 саны – саны –  жиынының жоғарғы шекараларының ең кішісі. Демек, жиынының жоғарғы шекараларының ең кішісі. Демек, 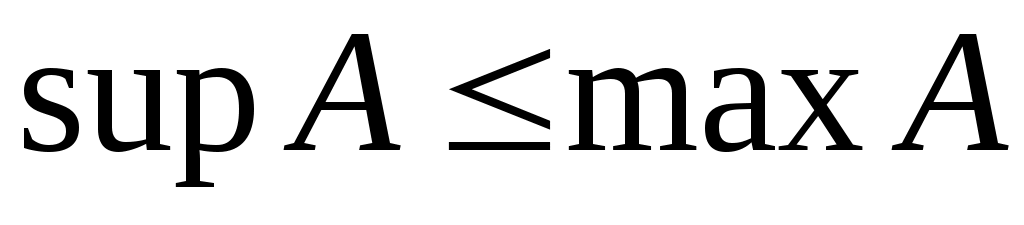 . .
Екінші жағынан, 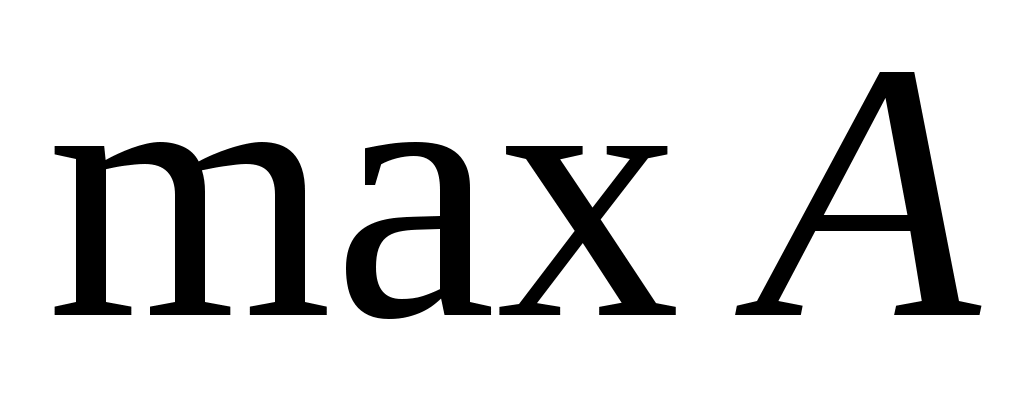 саны – саны – жиынының элементі, ал жиынының элементі, ал 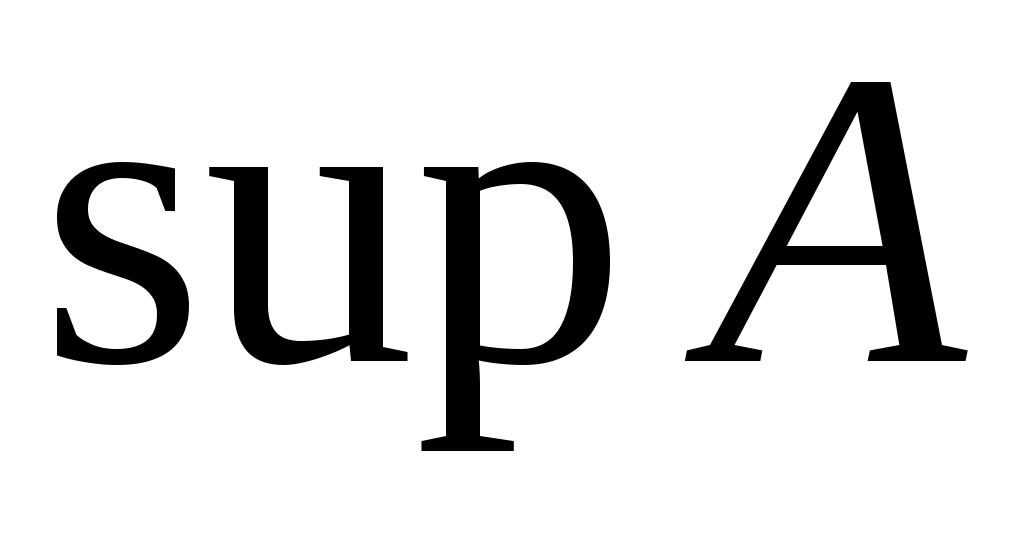 саны – саны –  жиынының жоғарғы шекарасы. Ендеше, жиынының жоғарғы шекарасы. Ендеше, 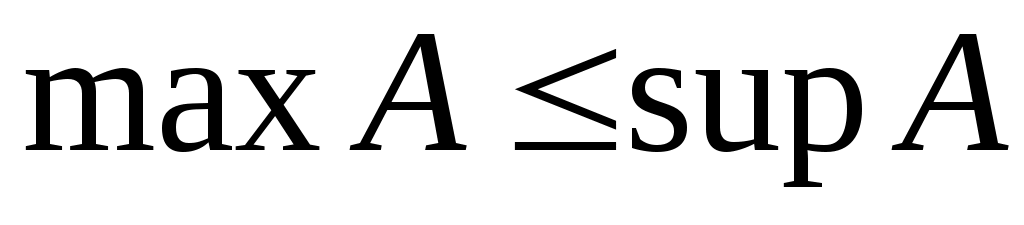 . .
Соңғы теңсіздіктерден: 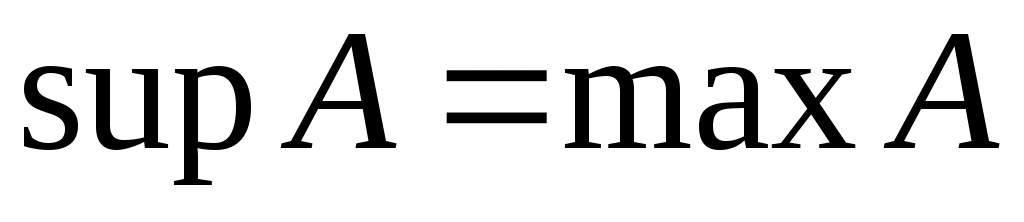 . . 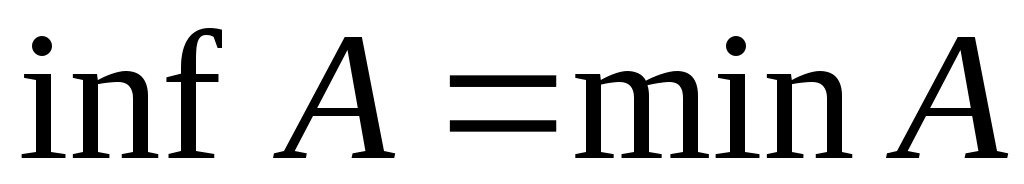 теңдігі де осылай көрсетіледі. теңдігі де осылай көрсетіледі.
2 – теорема. Егер  ( (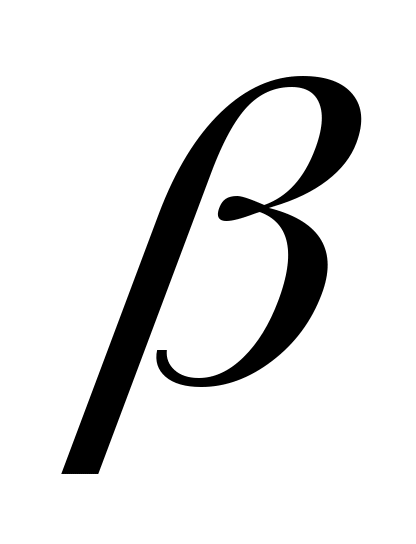 ) саны ) саны  жиынының жоғарғы (төменгі) шекара – сы болса, онда жиынының жоғарғы (төменгі) шекара – сы болса, онда 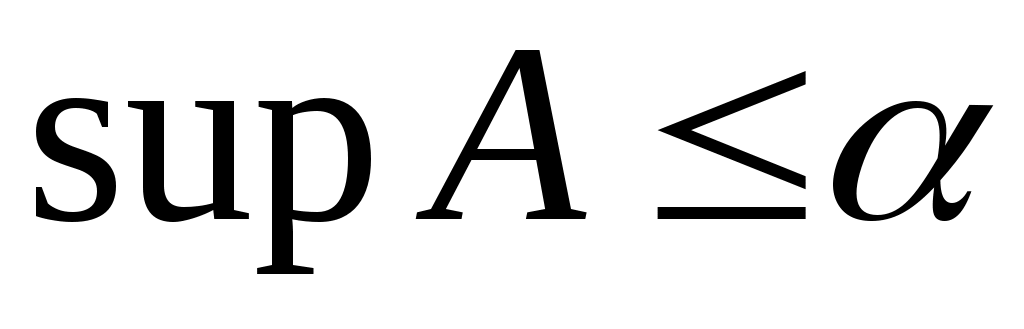 ( (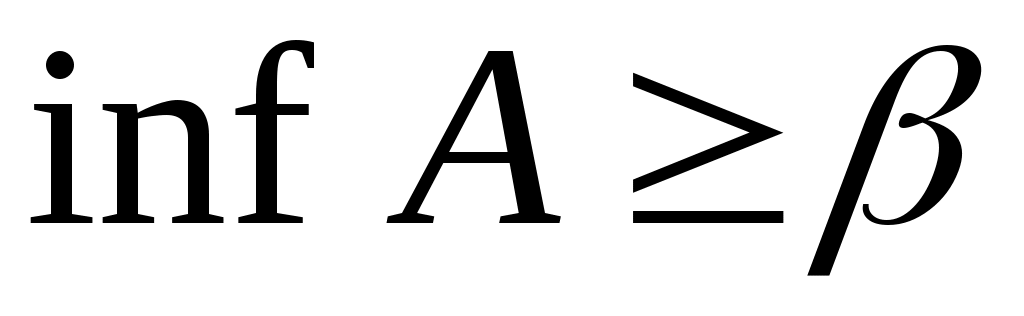 ). ).
Дәлелдеуі. 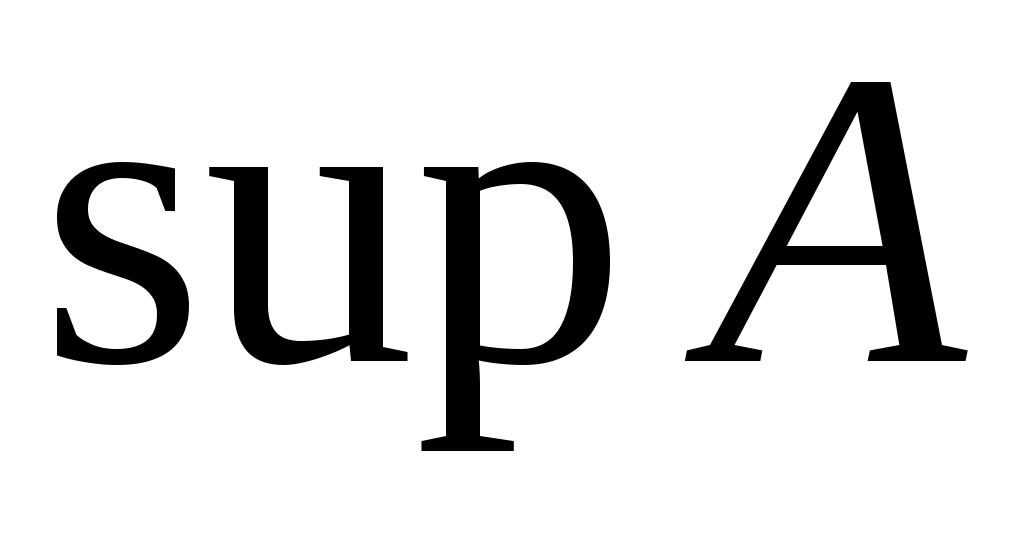 ( (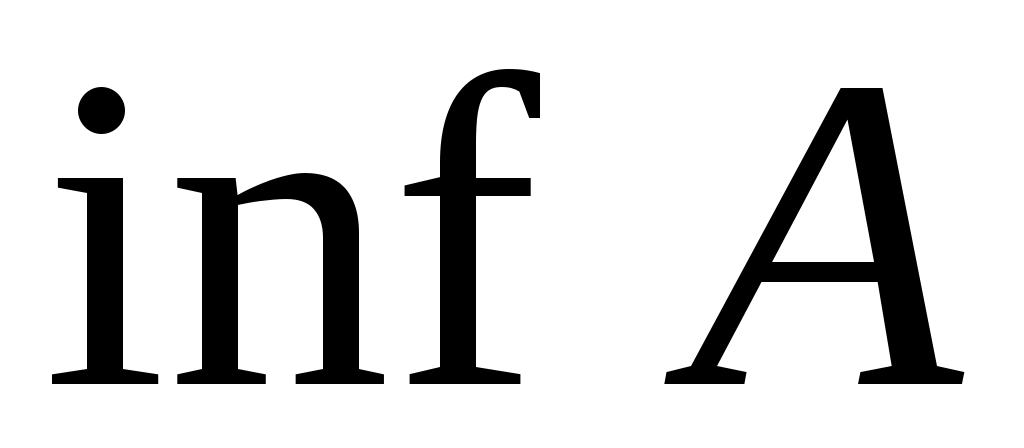 ) саны – ) саны –  жиынының жоғарғы (төменгі) шекара – лары жиынының ең кішісі (үлкені). Ендеше, жиынының жоғарғы (төменгі) шекара – лары жиынының ең кішісі (үлкені). Ендеше, 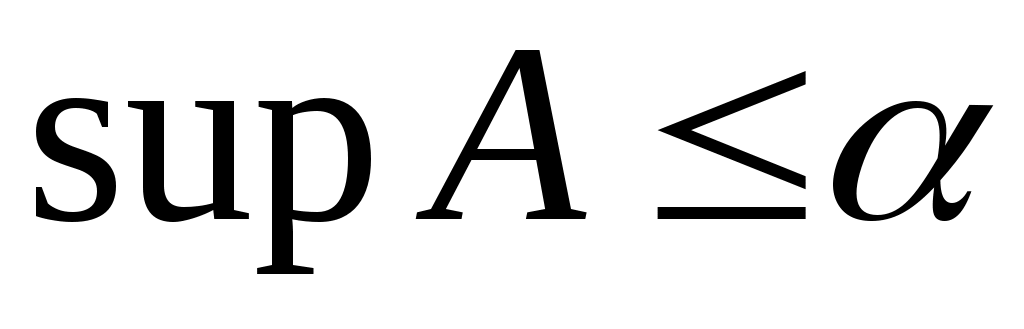 ( (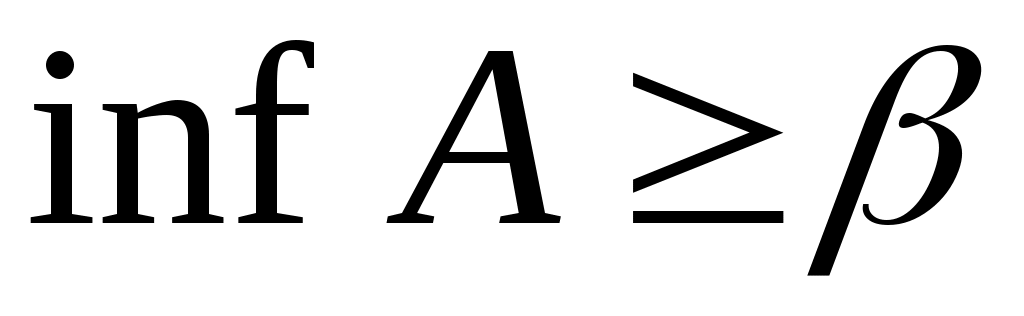 ). ).
3 – теорема. Егер  жиыны жоғарыдан (төменнен) шенелген болса, онда жиыны жоғарыдан (төменнен) шенелген болса, онда 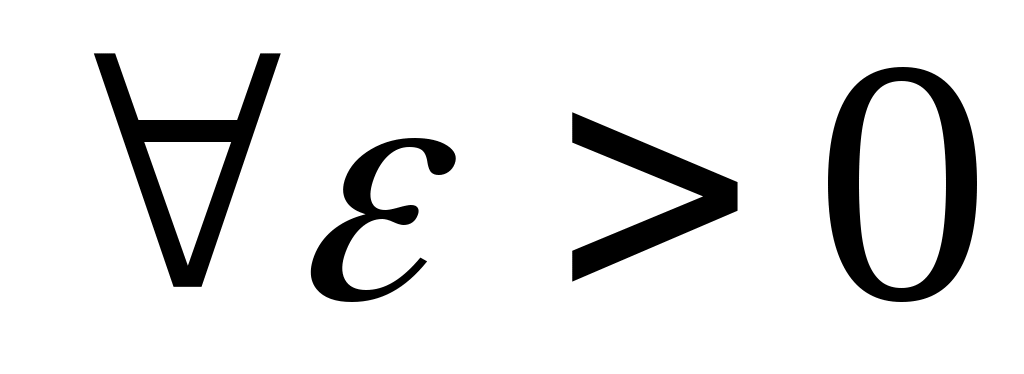 саны үшін саны үшін 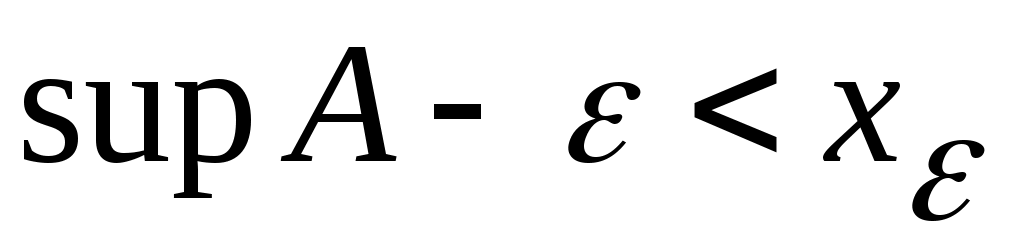 ( (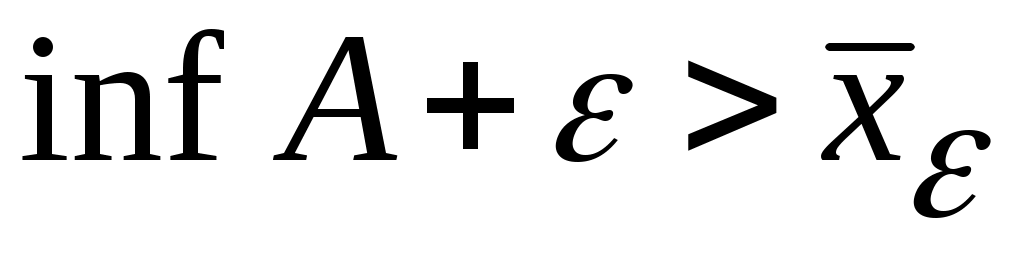 ) теңсіздігі орындалатындай ) теңсіздігі орындалатындай 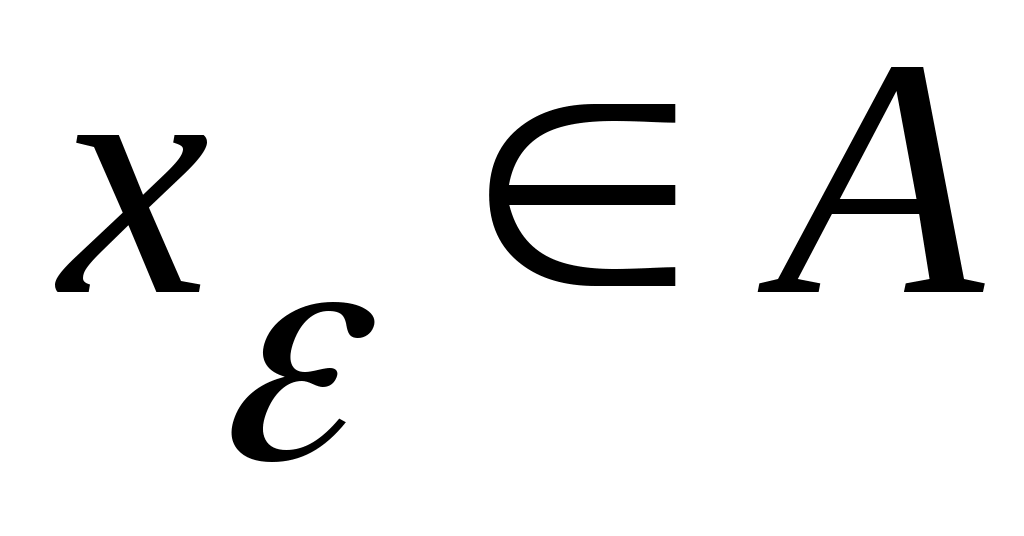 ( (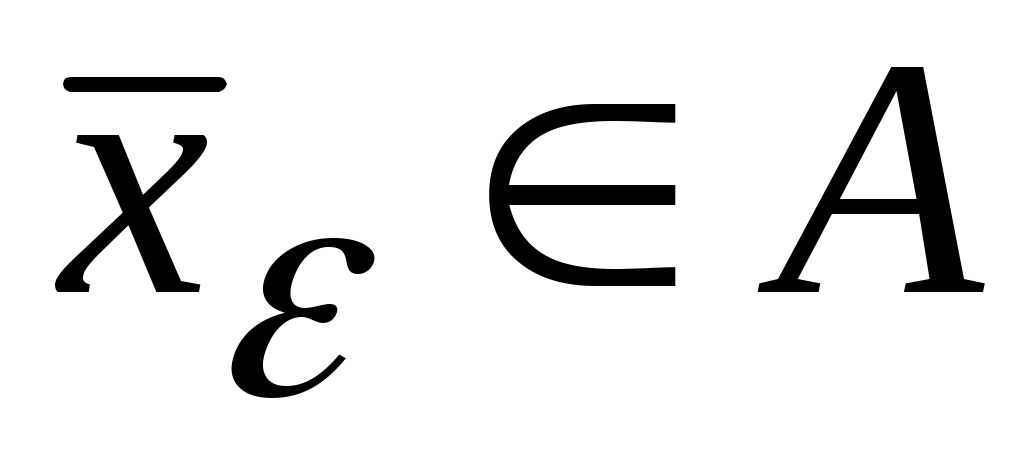 ) элементі табылады. ) элементі табылады.
Дәлелдеуі. 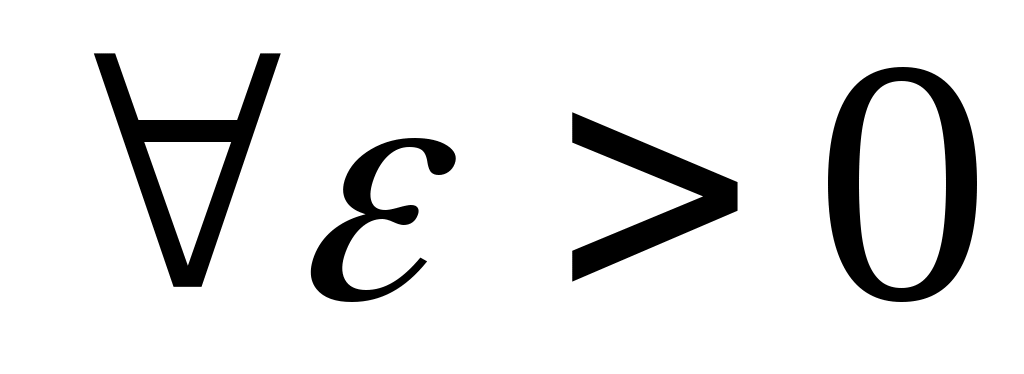 саны үшін саны үшін 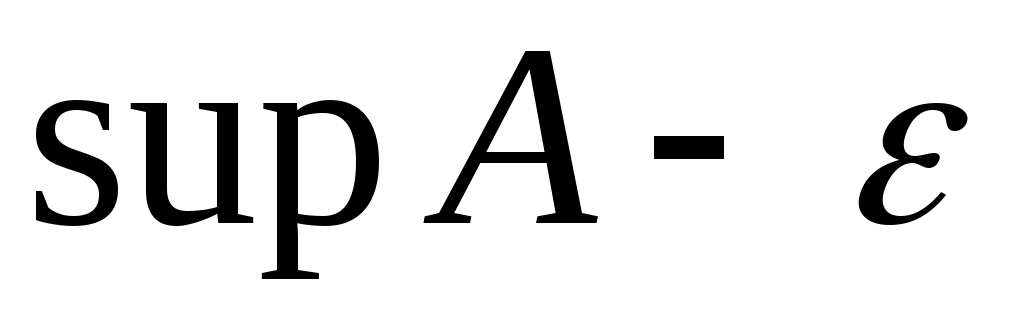 ( (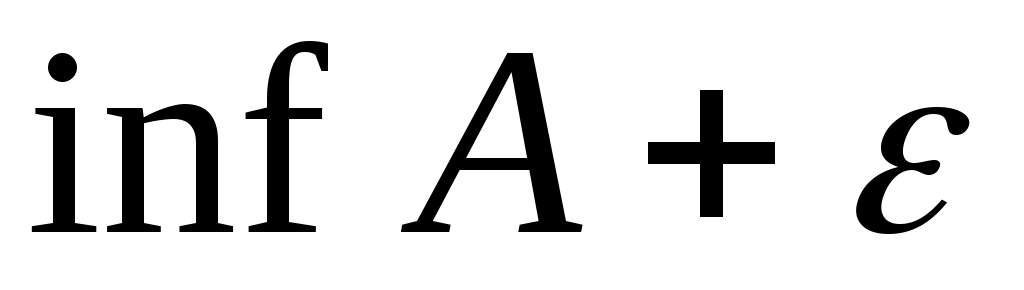 ) саны ) саны  жиынының жоғарғы (төменгі) шекарасы емес. Демек, қайсыбір жиынының жоғарғы (төменгі) шекарасы емес. Демек, қайсыбір 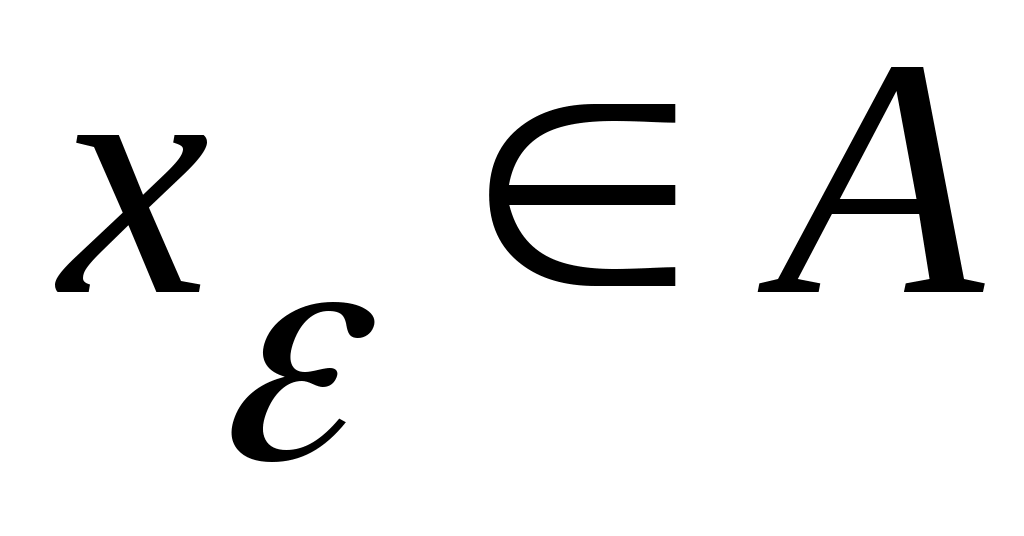 ( (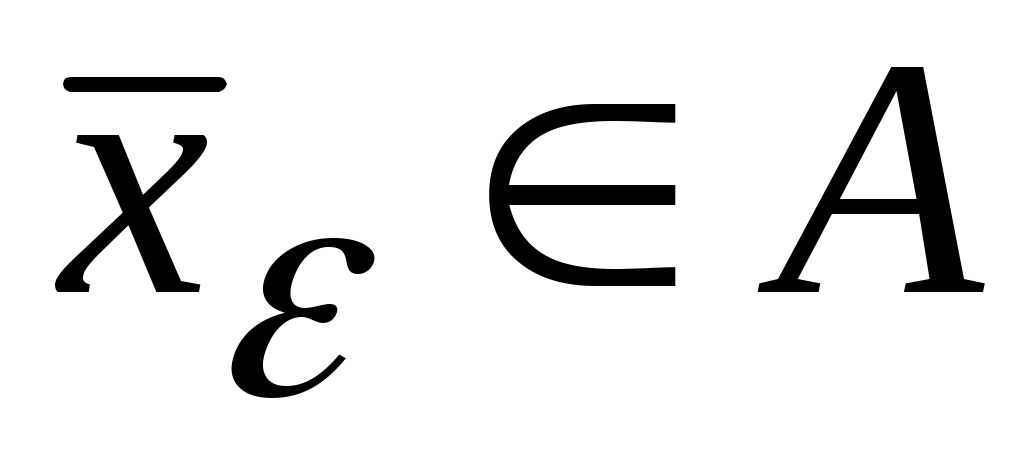 ) элементі ) элементі
үшін 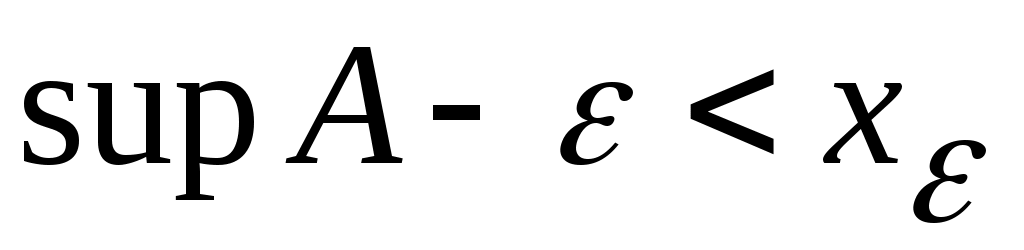 ( (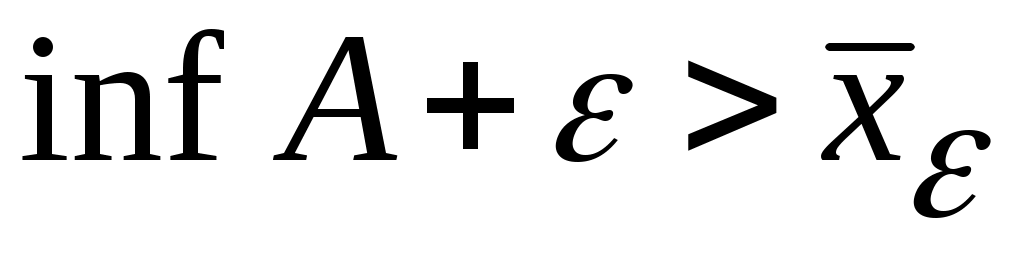 ) теңсіздігі орындалады. ) теңсіздігі орындалады.
4 – теорема. 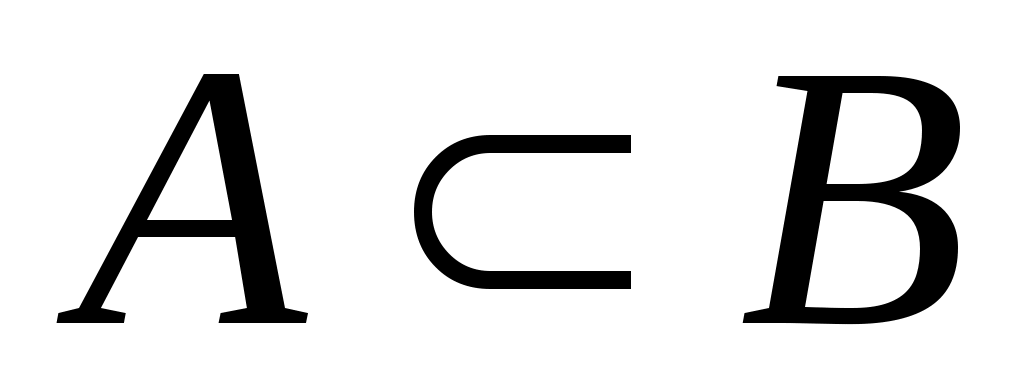 жиындары үшін жиындары үшін 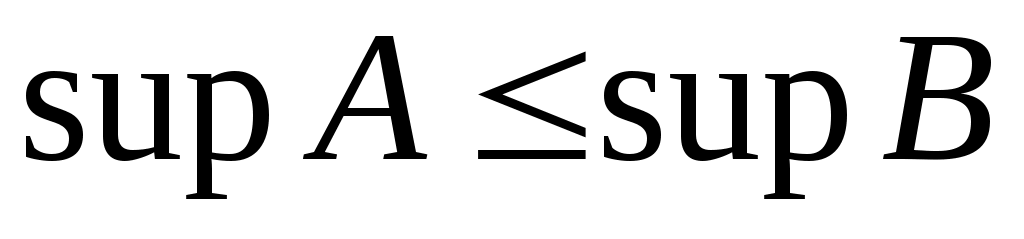 және және 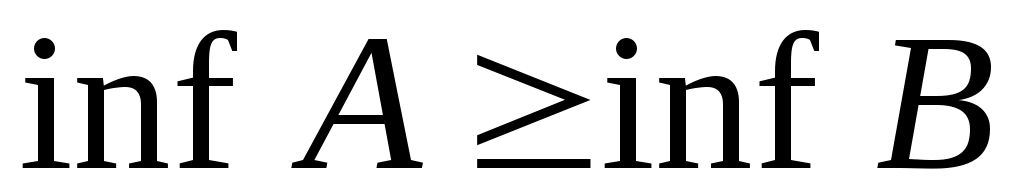
теңсіздіктері орындалады. Басқаша айтқанда, жиын кеңейген сайын супремум өседі, ал инфимум кемиді.
Дәлелдеуі. Егер 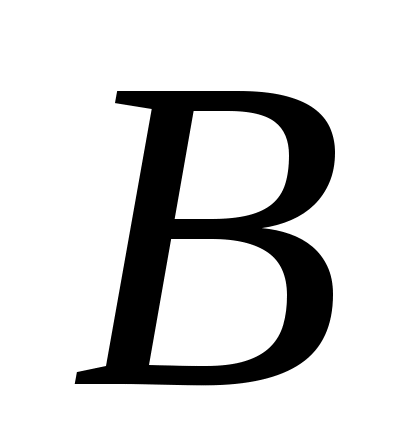 жиыны жоғарыдан шенелген болса, онда жиыны жоғарыдан шенелген болса, онда 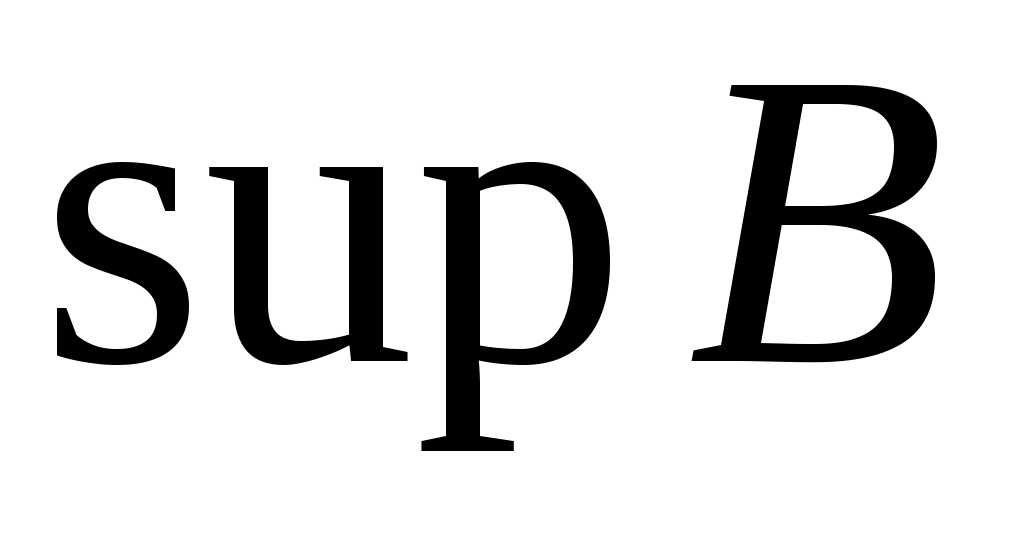 нақты сан болады және нақты сан болады және 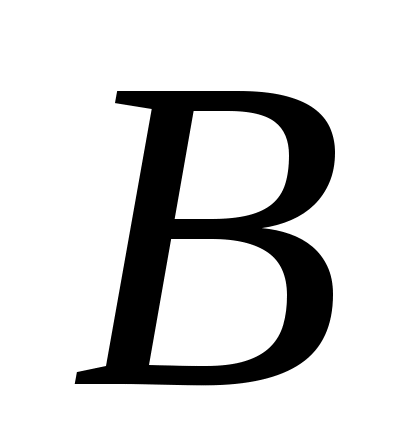 жиынының кез келген жиынының кез келген 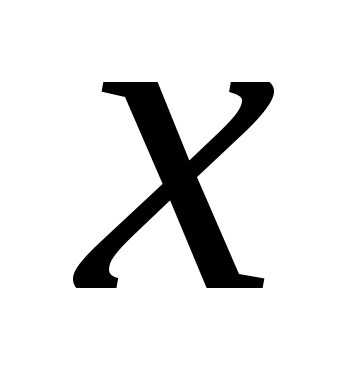 элементі элементі  теңсіздігін қанағаттандырады. теңсіздігін қанағаттандырады. 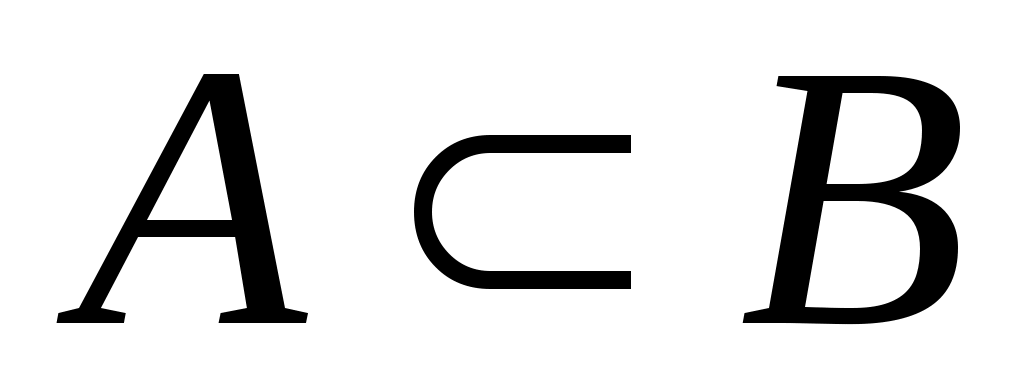 кірістіруінен кірістіруінен  жиынының әрбір жиынының әрбір 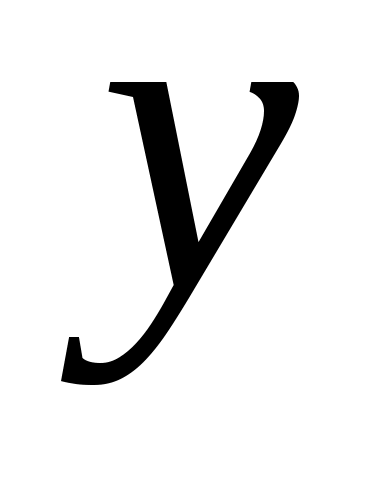 элементі үшін элементі үшін  теңсіздігі орындалатындығы шығады. Соңғы теңсіздік пен 2– теоремадан теңсіздігі орындалатындығы шығады. Соңғы теңсіздік пен 2– теоремадан 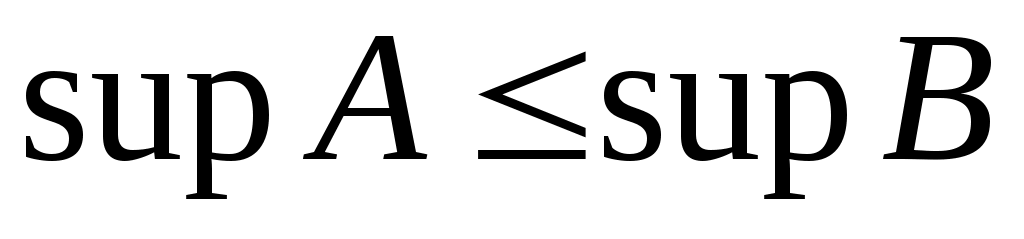 . Ал . Ал 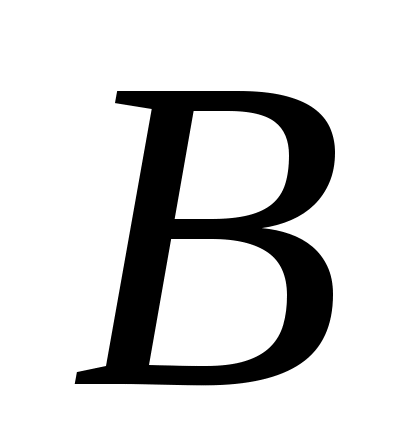 жиыны жоғарыдан шенелмеген болса, онда жиыны жоғарыдан шенелмеген болса, онда 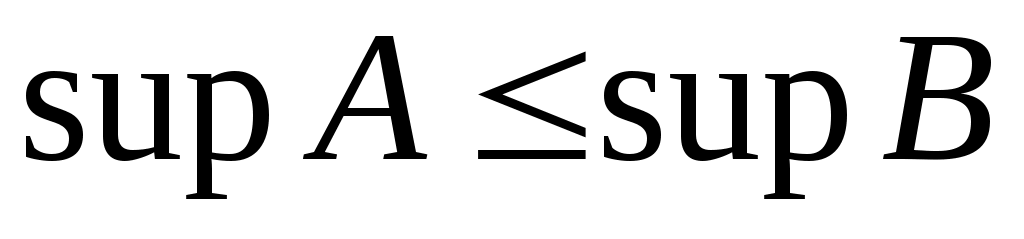 теңсіздігі әлбетте орындалады, өйткені, теңсіздігі әлбетте орындалады, өйткені, 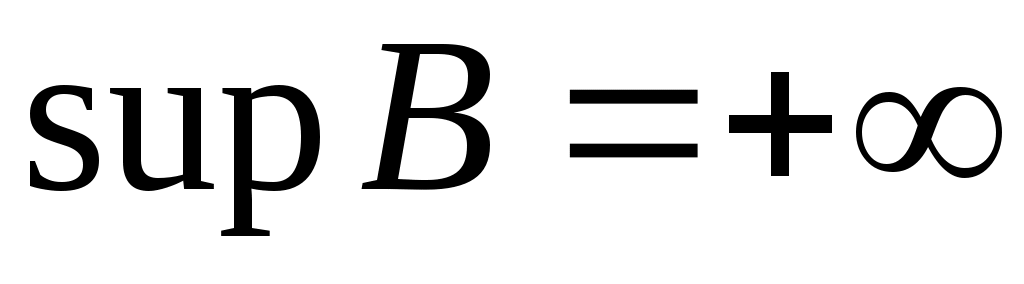 . . 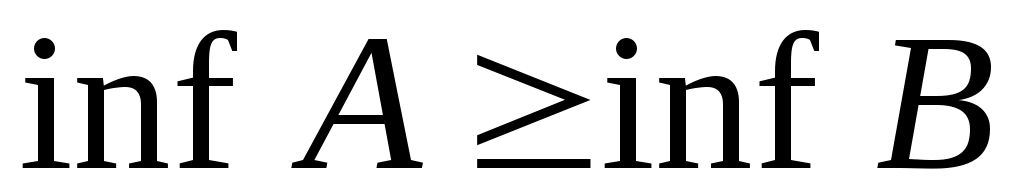 теңсіздігі де осылай көрсетіледі. теңсіздігі де осылай көрсетіледі.
5 – теорема.  , ,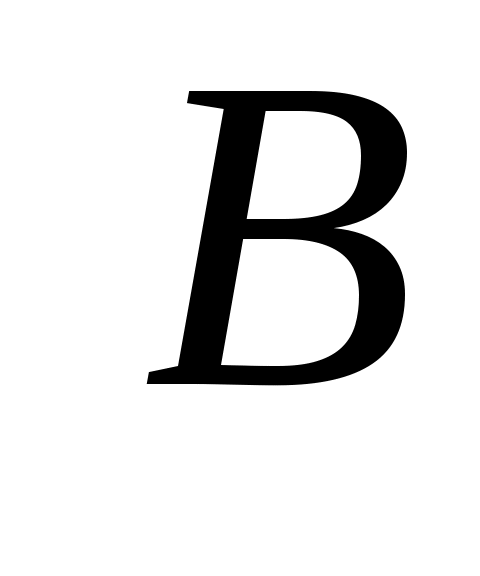 жиындары берілсін. Егер кез келген жиындары берілсін. Егер кез келген  және және 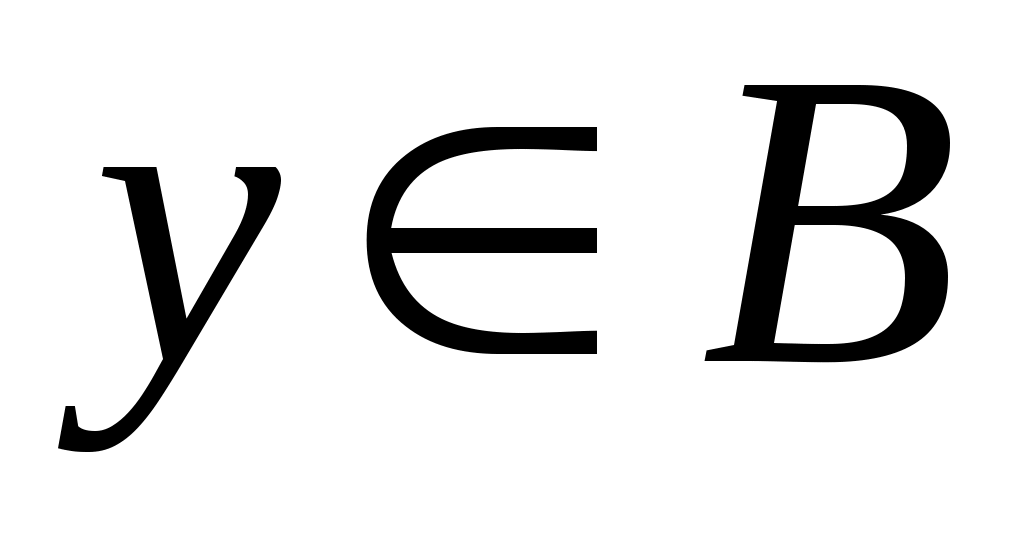 элементтері үшін элементтері үшін 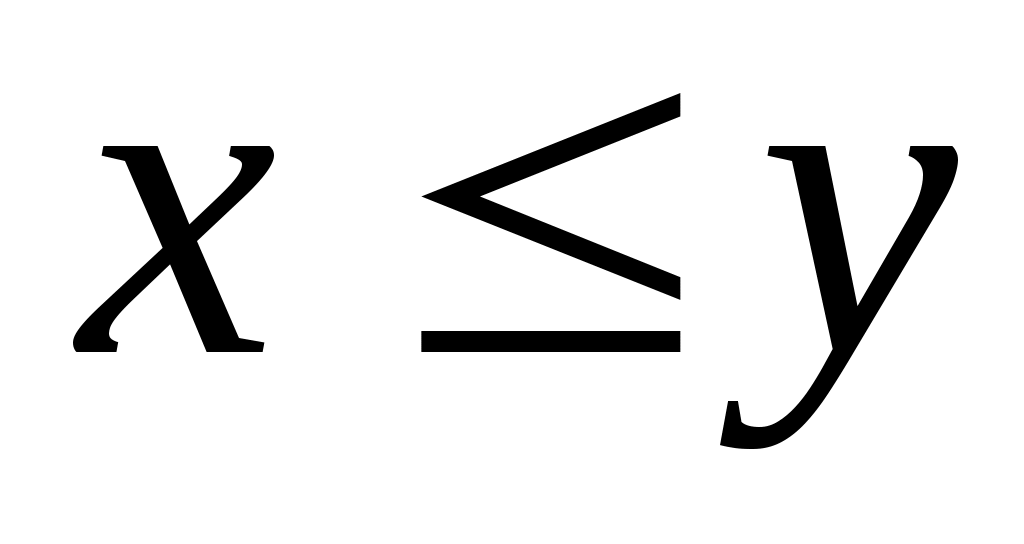 теңсіздігі орындалса, онда теңсіздігі орындалса, онда 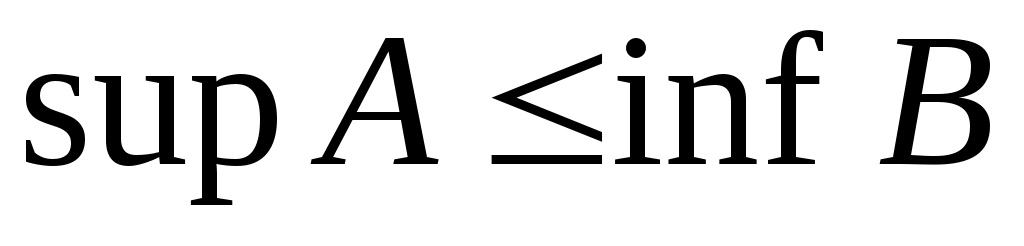 . .
Дәлелдеуі. 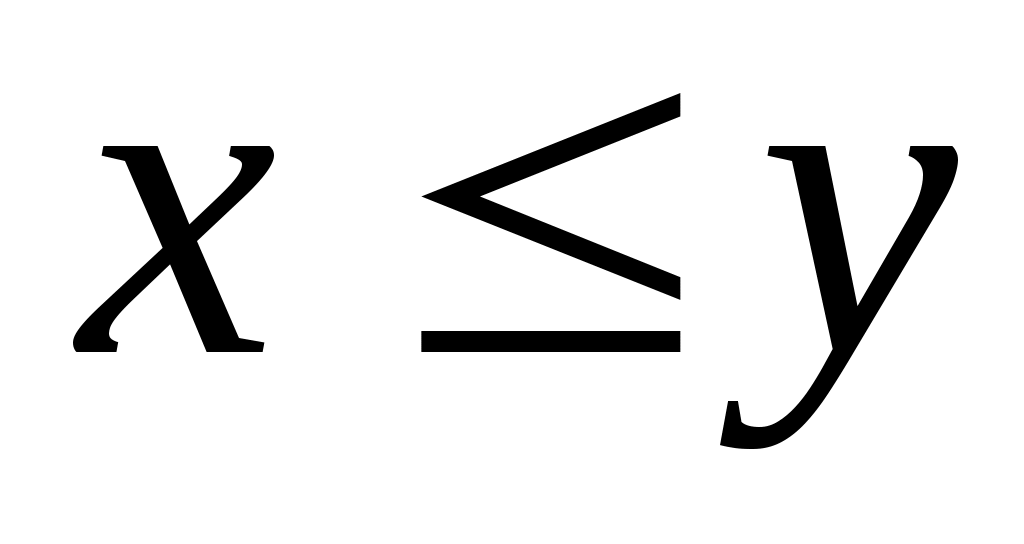 теңсіздігі бойынша әрбір теңсіздігі бойынша әрбір 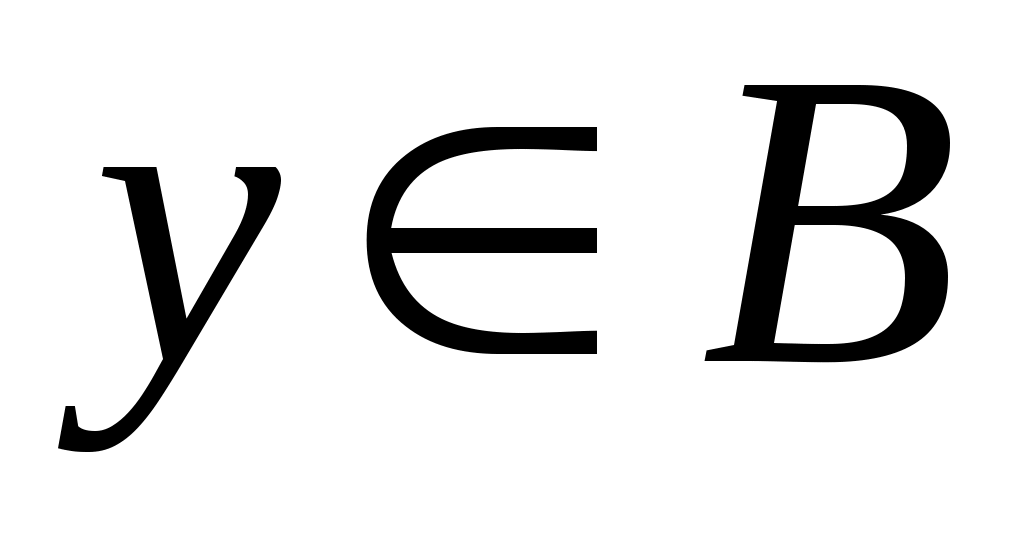 элементі – элементі –  жиынының жоғарғы шекарасы. Демек, барлық жиынының жоғарғы шекарасы. Демек, барлық 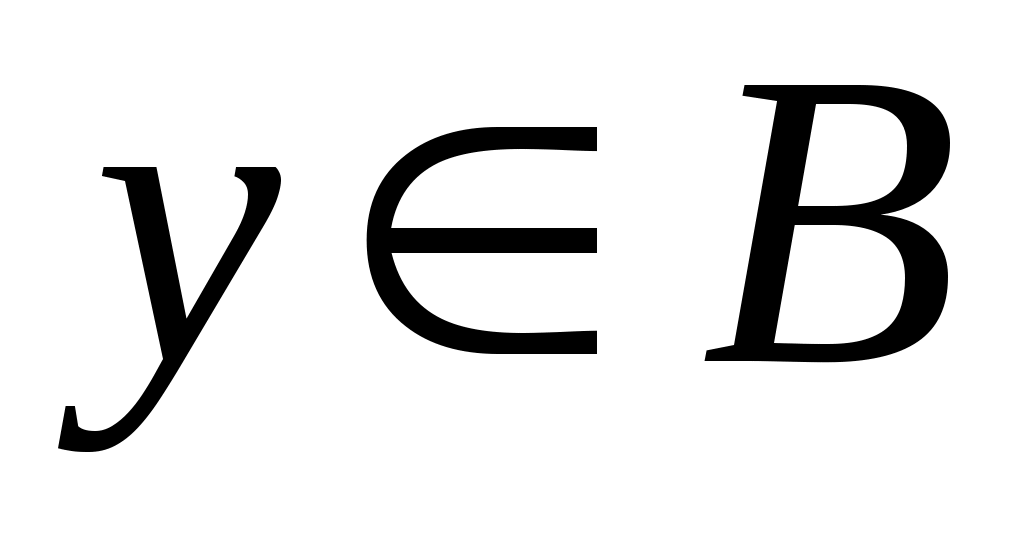 үшін үшін 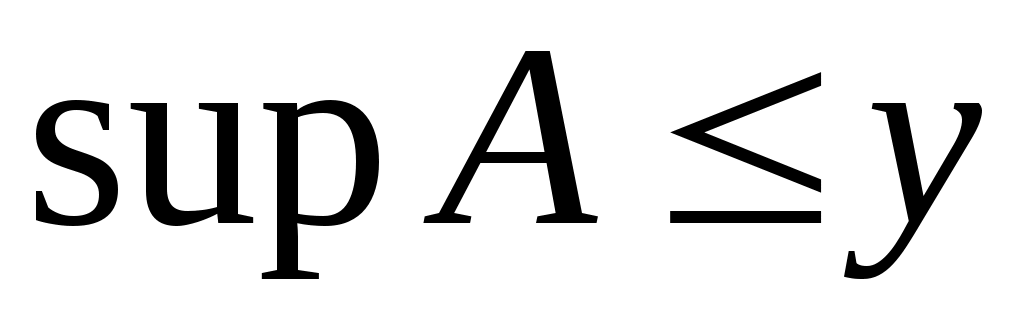 теңсіздігі орындалады. Енді 2 – теореманы ескерсек, теңсіздігі орындалады. Енді 2 – теореманы ескерсек, 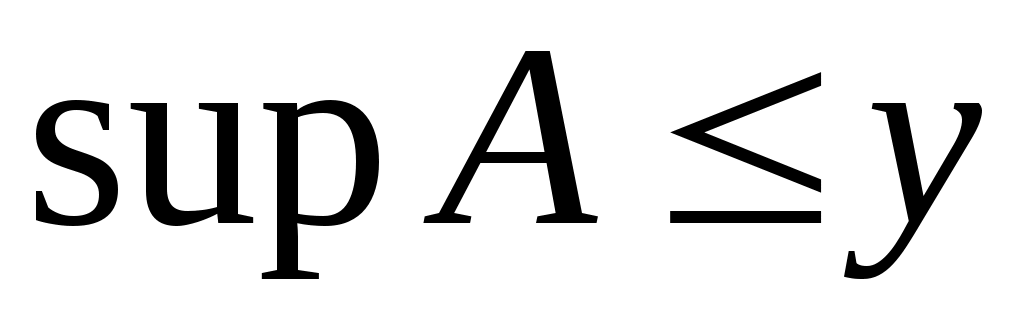 теңсіздігінен теңсіздігінен 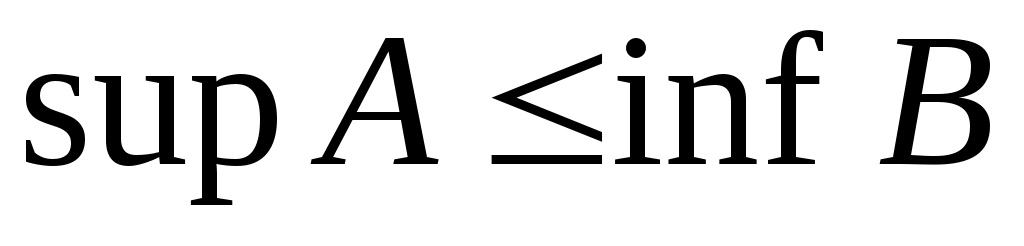 теңсіздігін аламыз. теңсіздігін аламыз.
6 – теорема. Егер  жиыны шенелген болса,онда а) әрбір жиыны шенелген болса,онда а) әрбір 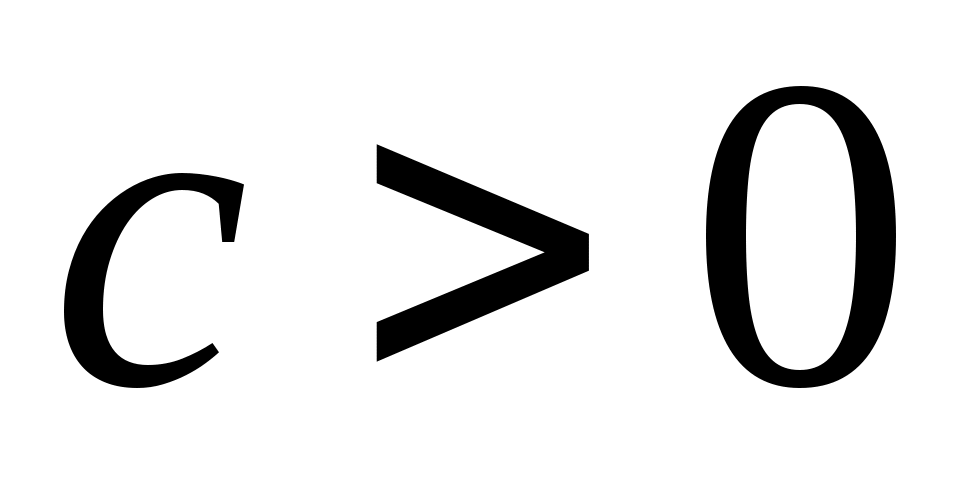 үшін үшін  ; ә) әрбір ; ә) әрбір 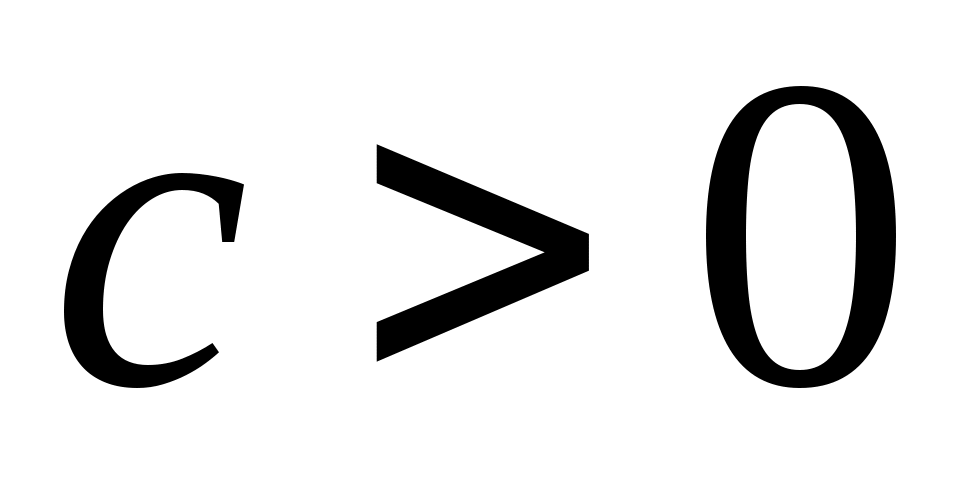 үшін үшін 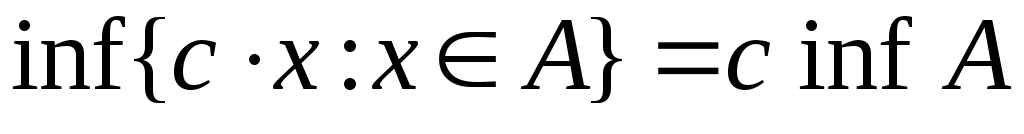 ; б) әрбір ; б) әрбір 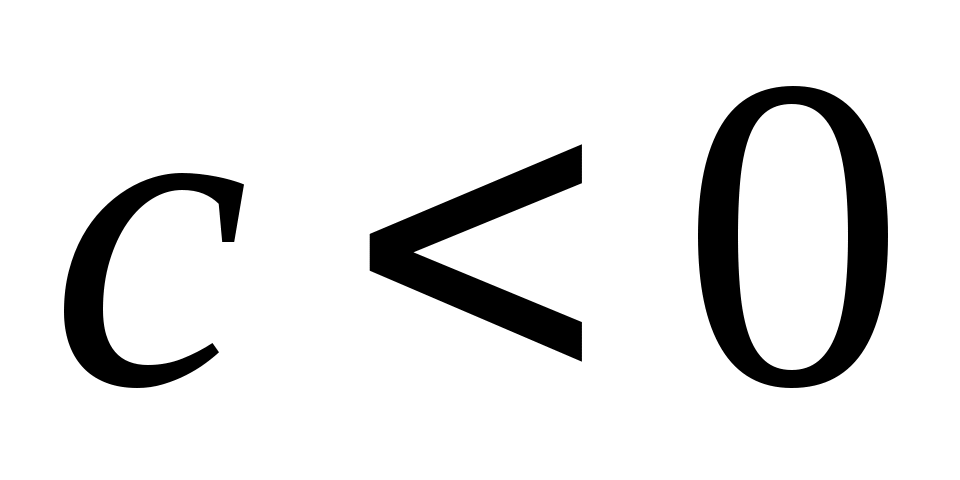 үшін үшін  ; в) әрбір ; в) әрбір 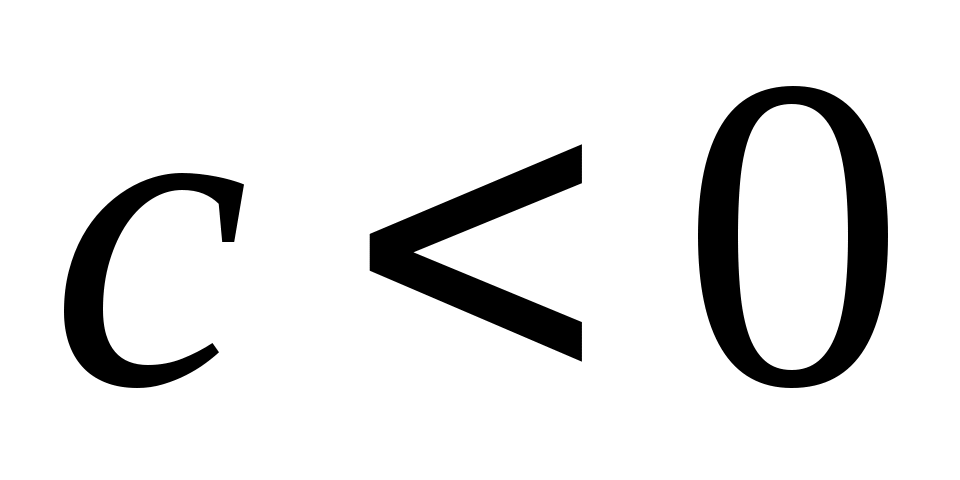 үшін үшін  . .
Дәлелдеуі. а) жағдайын дәлелдейік. 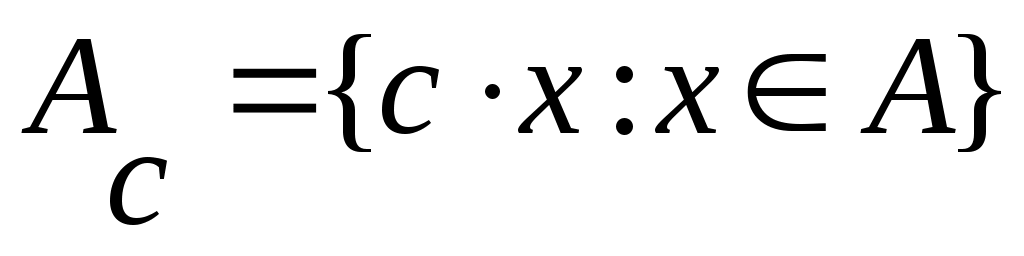 , , 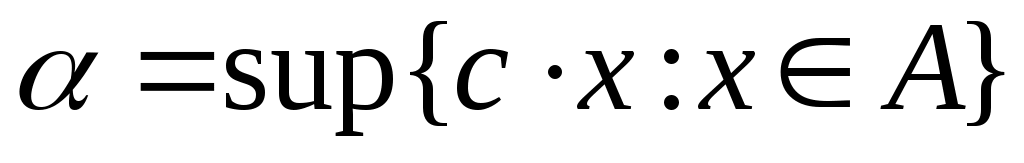 , , 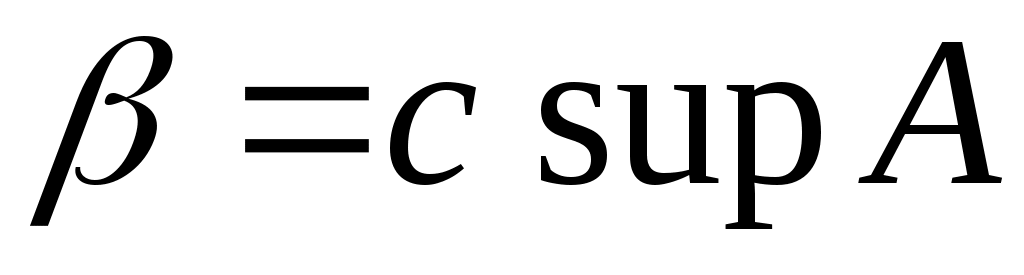 болсын. Енді болсын. Енді 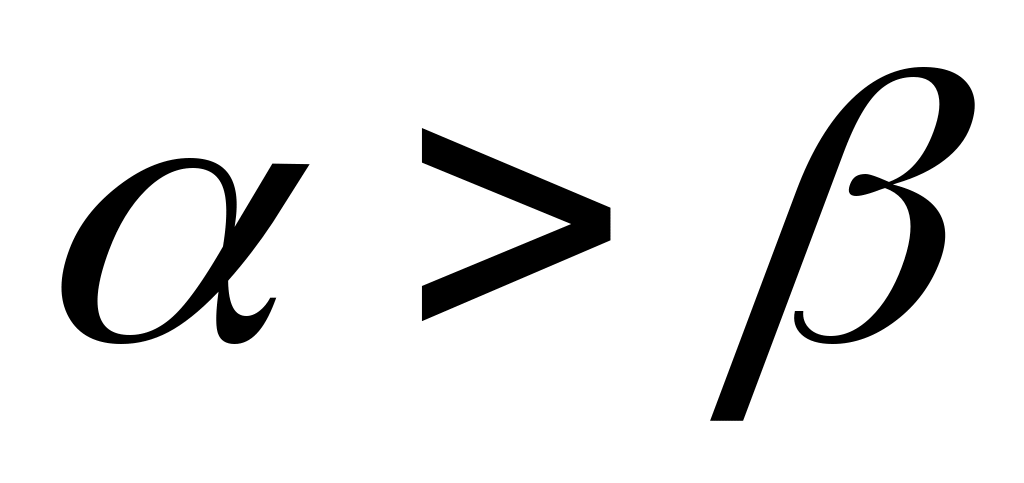 теңсіздігі де, теңсіздігі де, 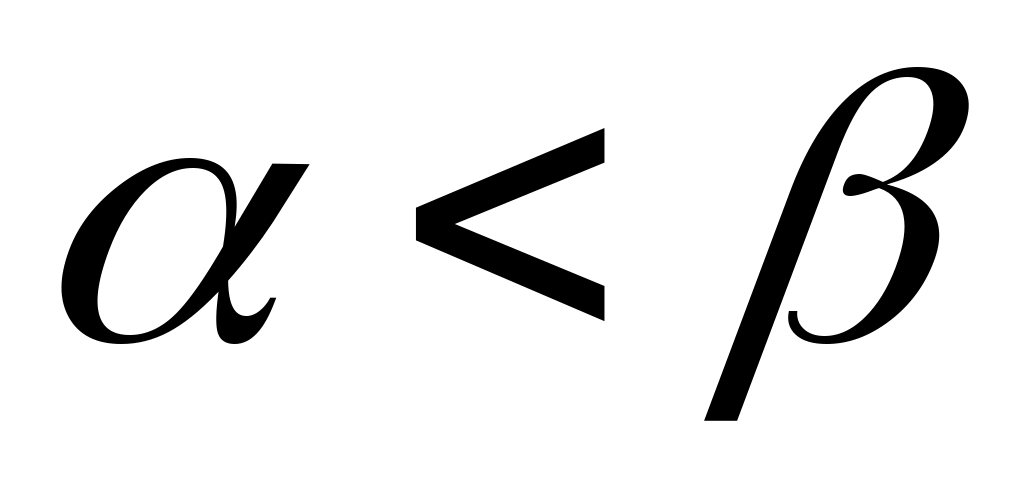 теңсіздігі де орындалмай – тынына көз жеткізейік. Егер теңсіздігі де орындалмай – тынына көз жеткізейік. Егер 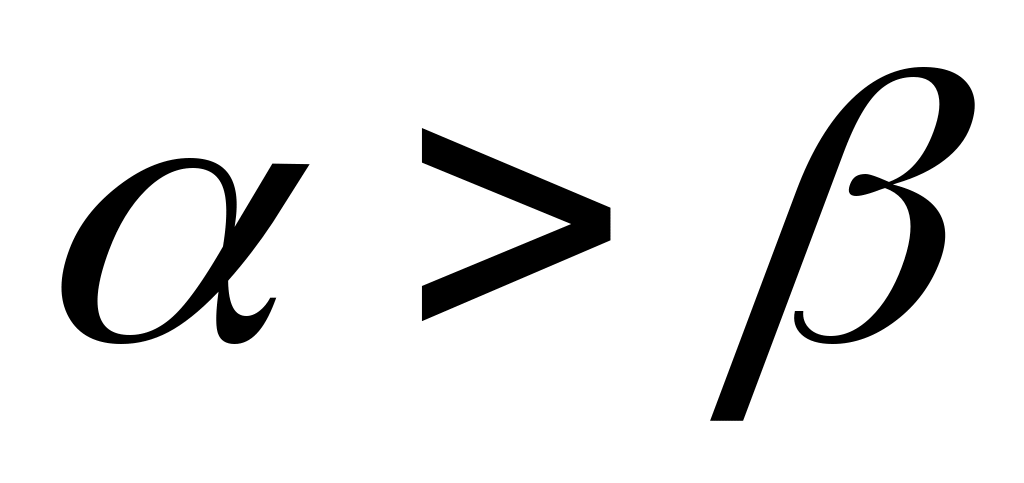 болса, онда болса, онда 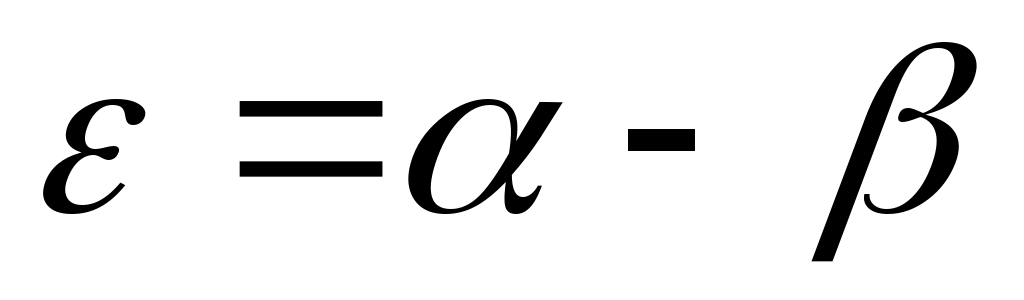 саны үшін саны үшін
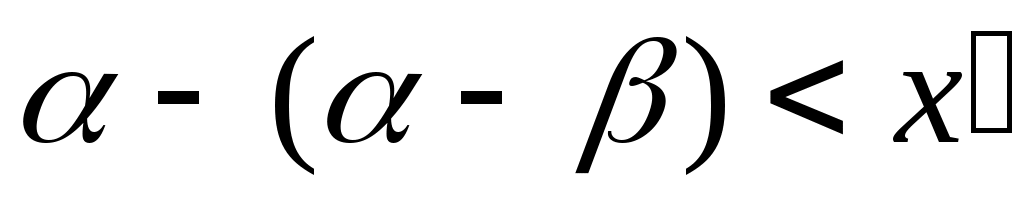 теңсіздігі орындалатын теңсіздігі орындалатын  элементі табылады (қараңыз, 3– теорема). Демек, қайсыбір элементі табылады (қараңыз, 3– теорема). Демек, қайсыбір  үшін үшін 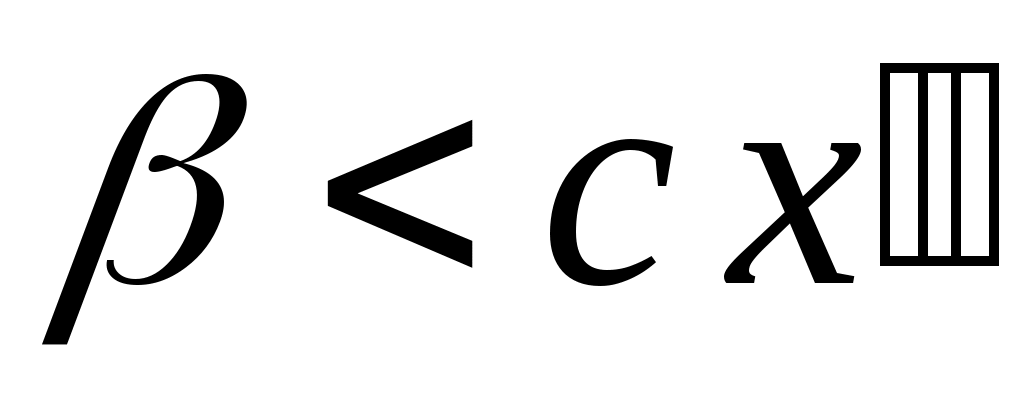 теңсіздігін жаза аламыз. Ал бұл теңсіздік теңсіздігін жаза аламыз. Ал бұл теңсіздік 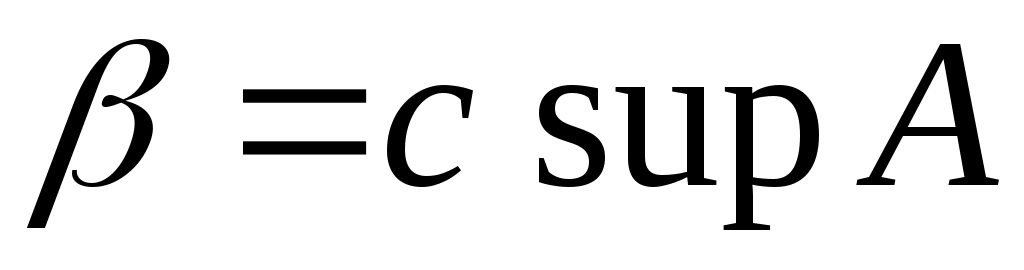 теңдігінен шығатын теңдігінен шығатын 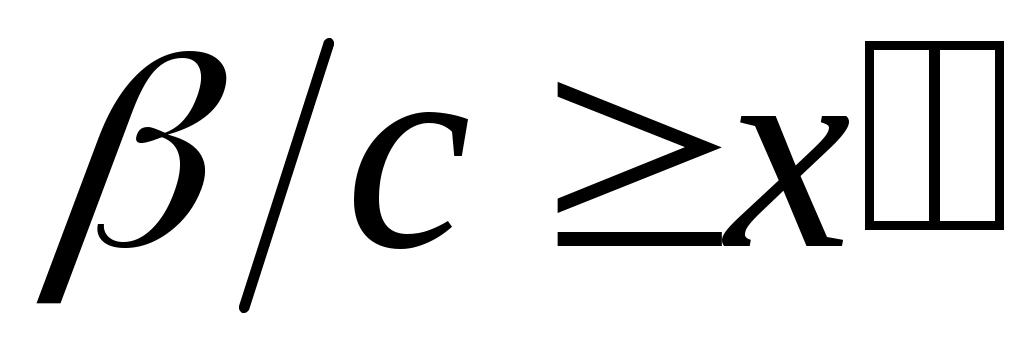 теңсіздігіне қайшы. Ендеше, теңсіздігіне қайшы. Ендеше, 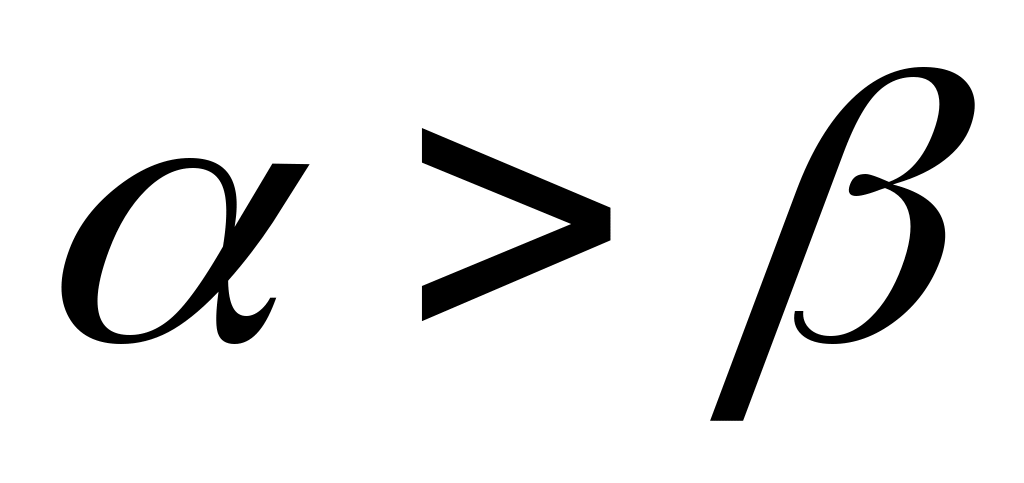 теңсіздігі орындалмайды. Егер теңсіздігі орындалмайды. Егер 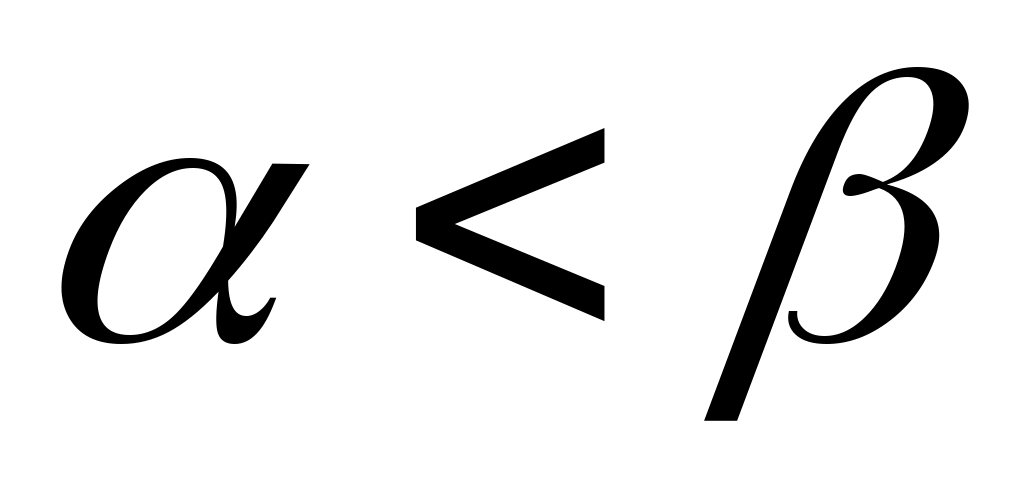 болса, онда болса, онда 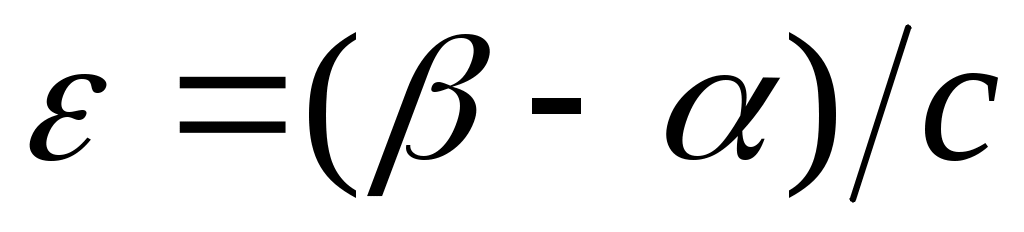 саны үшін саны үшін
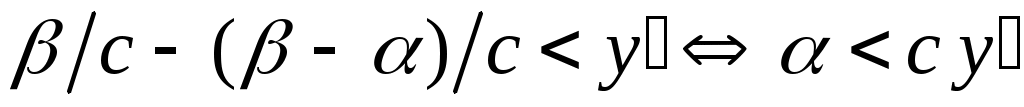
теңсіздігі орындалатын  элементі бар болады. Ал элементі бар болады. Ал 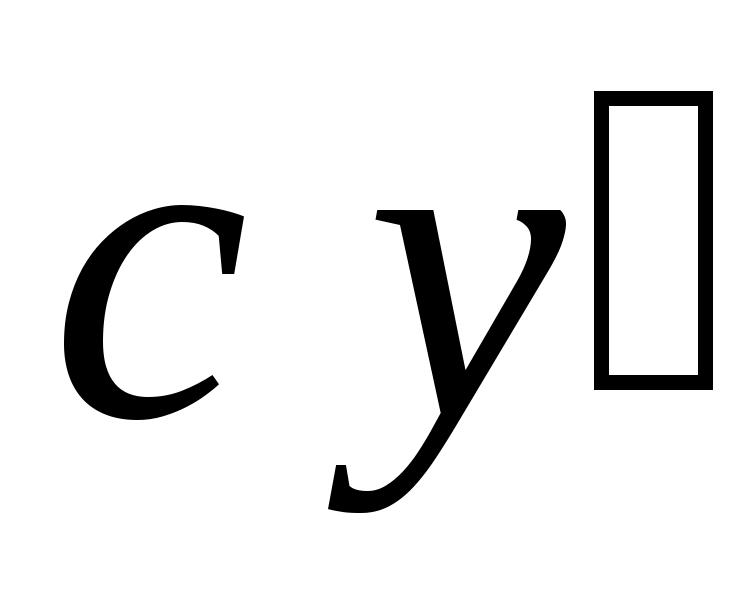 элементі элементі 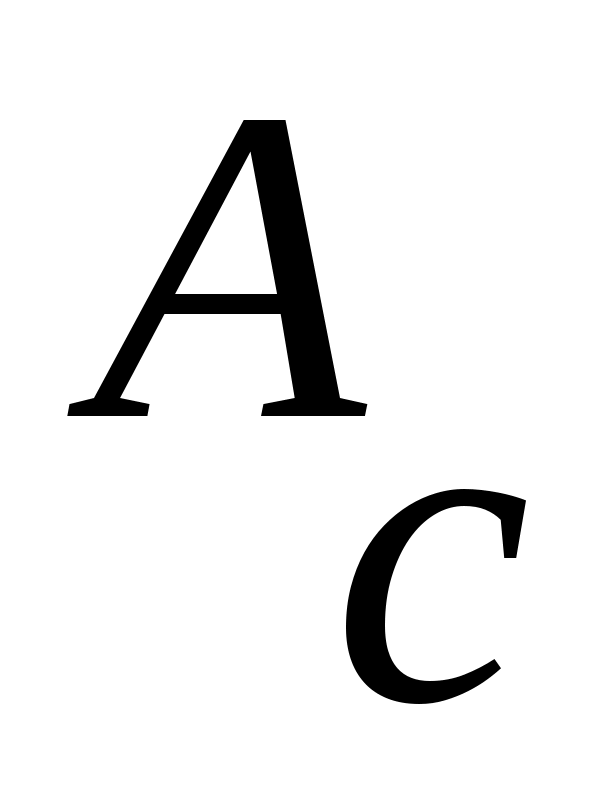 жиынында жататынын ескерсек, жиынында жататынын ескерсек, 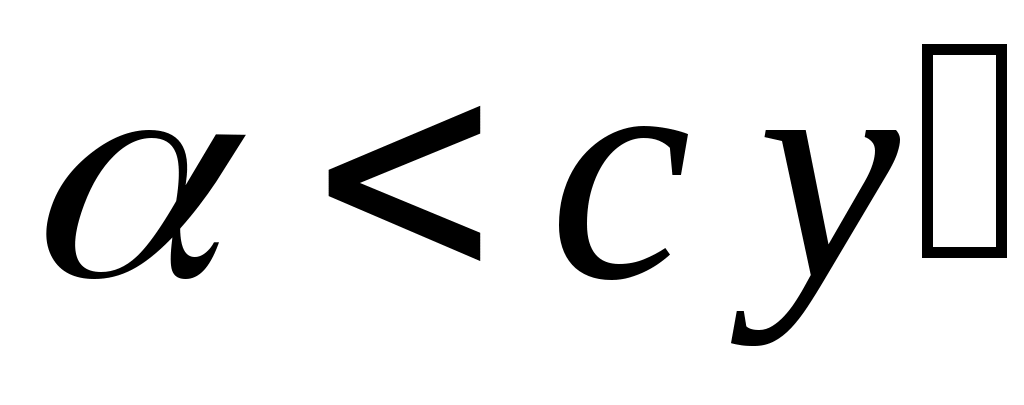 теңсіздігі теңсіздігі 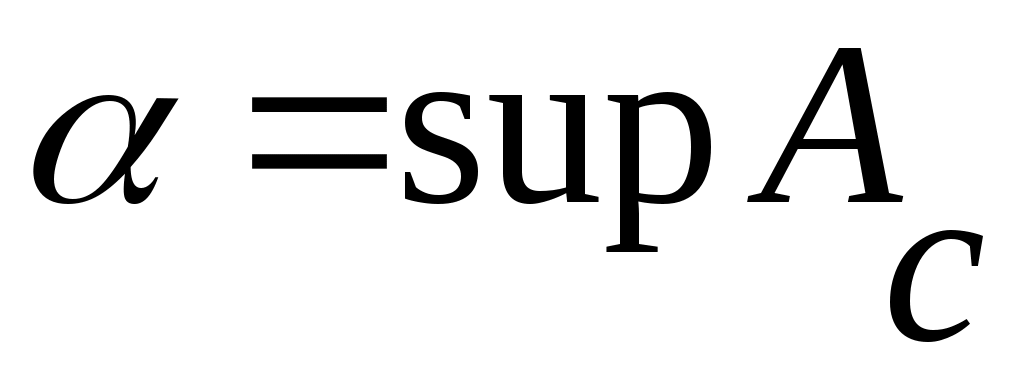 теңдігінен шығатын теңдігінен шығатын 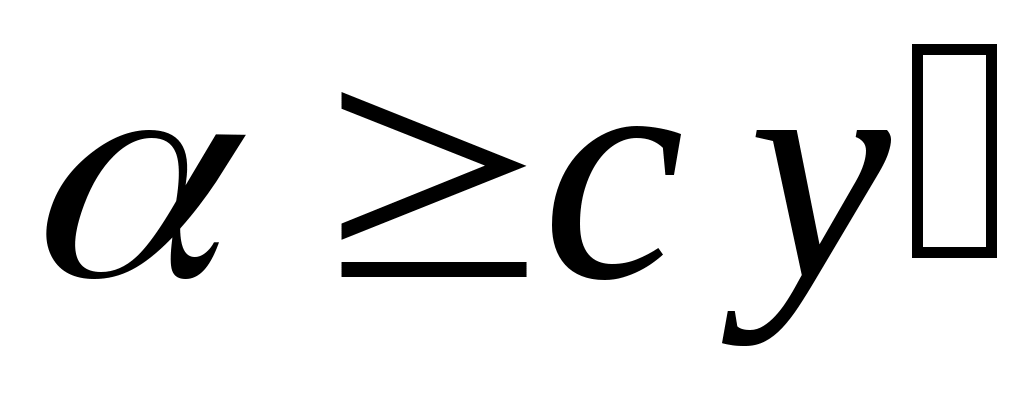 теңсіздігіне қайшы. Ендеше, теңсіздігіне қайшы. Ендеше, 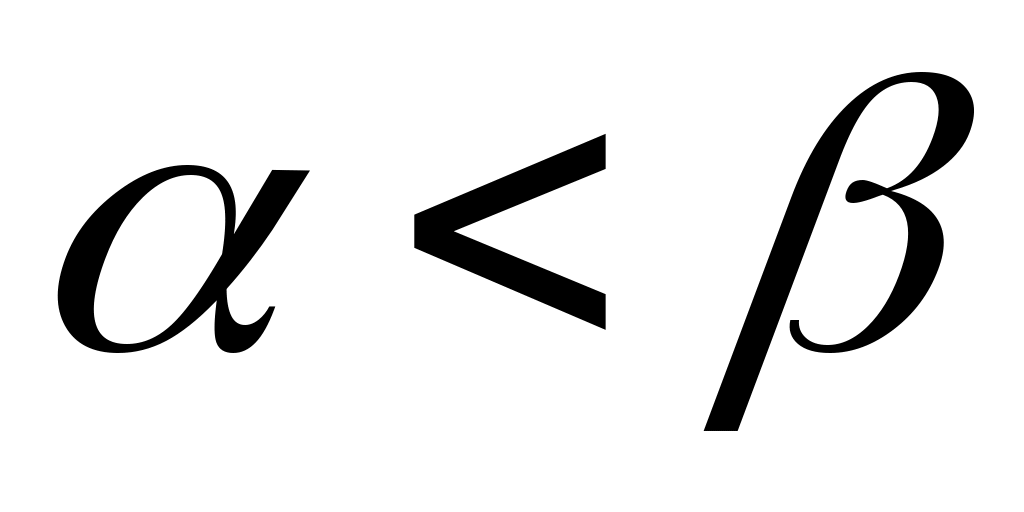 теңсіздігі де орындал – майды. Сонымен, теңсіздігі де орындал – майды. Сонымен,  және және 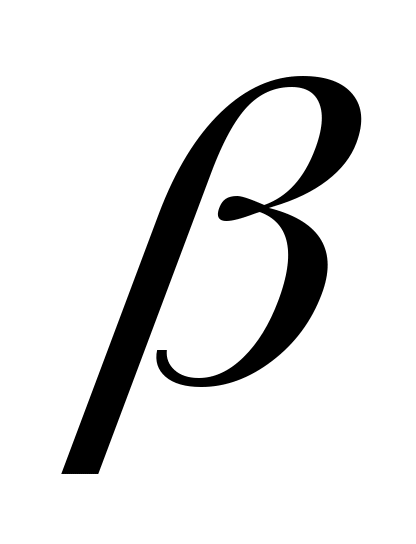 сандары үшін сандары үшін 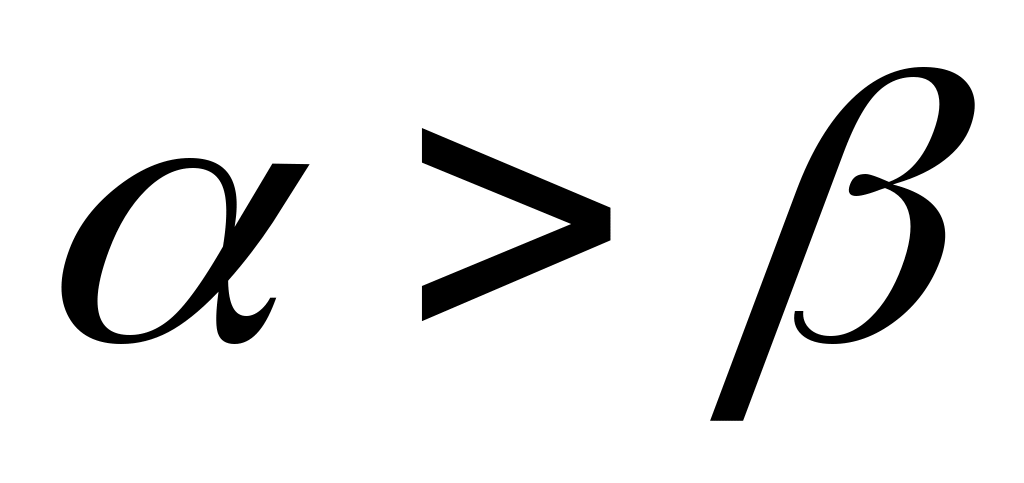 теңсіздігі де, теңсіздігі де, 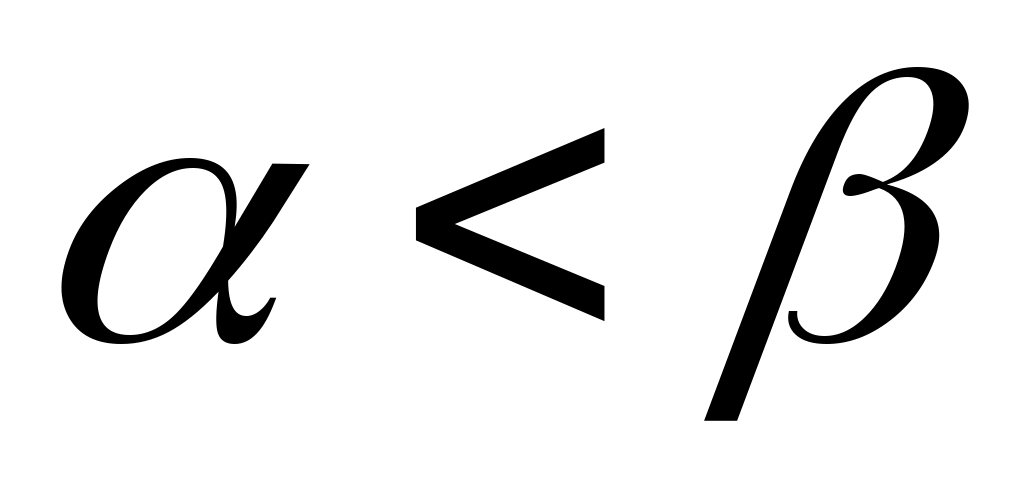 теңсіздігі де орындалмайды екен. Демек, теңсіздігі де орындалмайды екен. Демек, 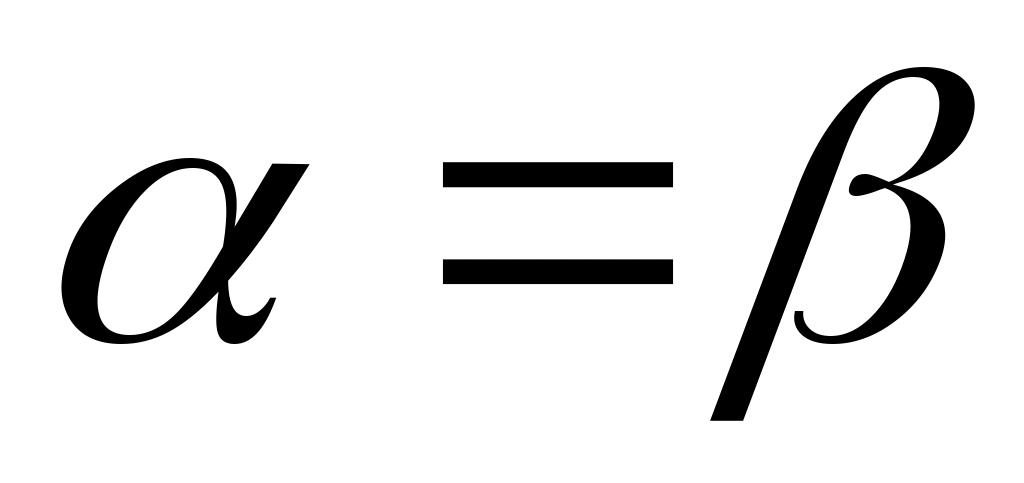 . ә), б), в) жағдайлары да осылай дәлелденеді. . ә), б), в) жағдайлары да осылай дәлелденеді.
7 – теорема. Егер  жиыны жоғарыдан шенелгенболса, 1) жиыны жоғарыдан шенелгенболса, 1) 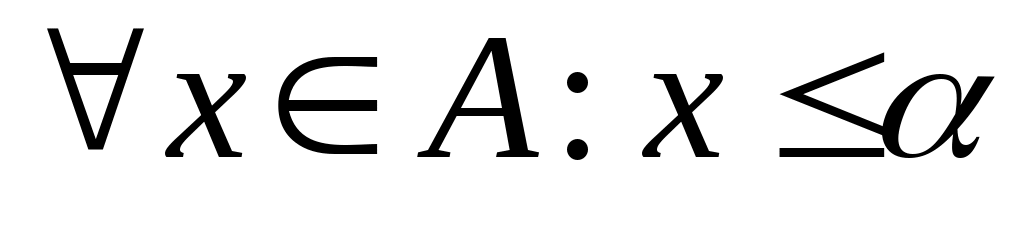 ; ;
2)  шарттарын қанағаттандыратын шарттарын қанағаттандыратын  саны саны  жиынының супремумі болады. жиынының супремумі болады.
Дәлелдеуі. 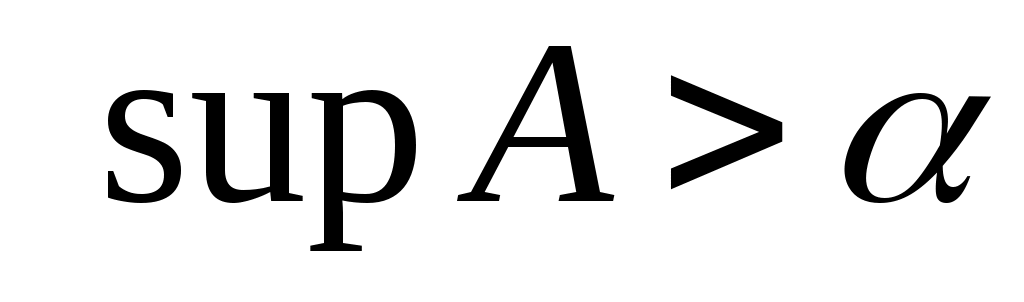 және және 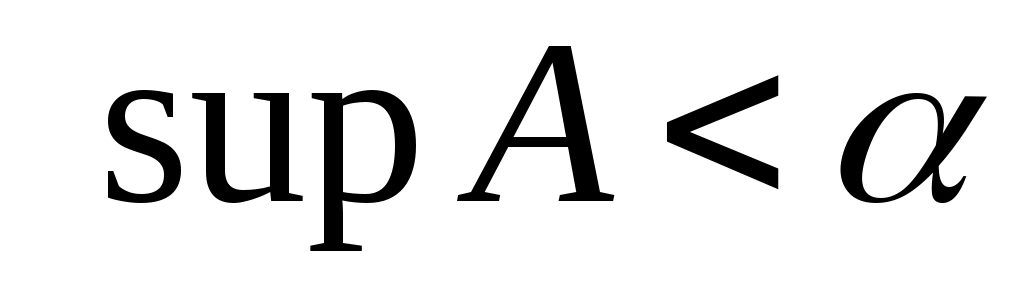 теңсіздіктерінің орындалмайтынын көрсетсек болғаны. Егер теңсіздіктерінің орындалмайтынын көрсетсек болғаны. Егер 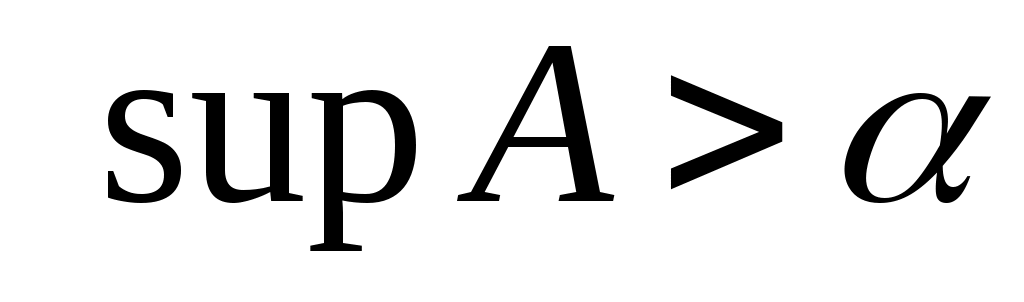 теңсіздігі орындалады десек, онда теңсіздігі орындалады десек, онда
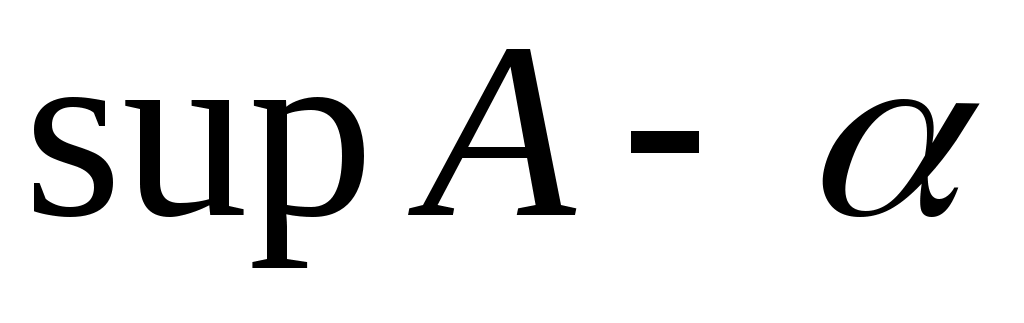 айырмасы оң болады. 3 – теоремадағы айырмасы оң болады. 3 – теоремадағы 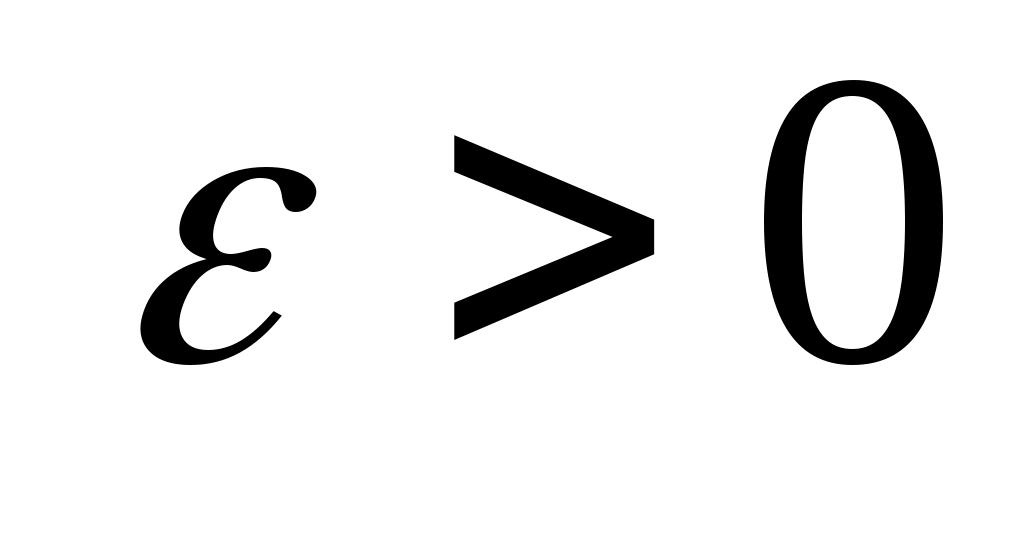 саны ретінде саны ретінде 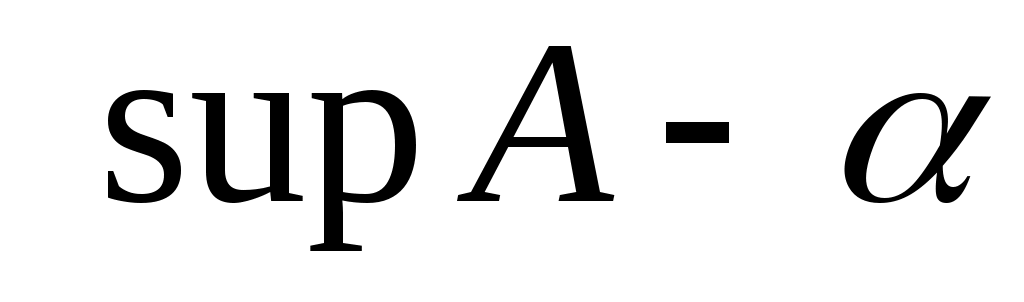
санын алсақ, 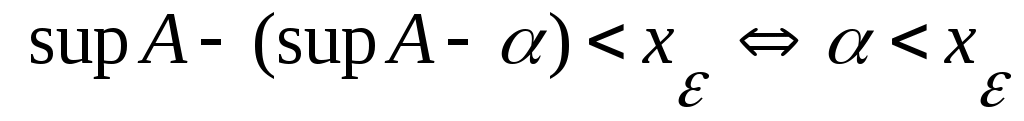 теңсіздігіне келеміз. Ал теңсіздігіне келеміз. Ал 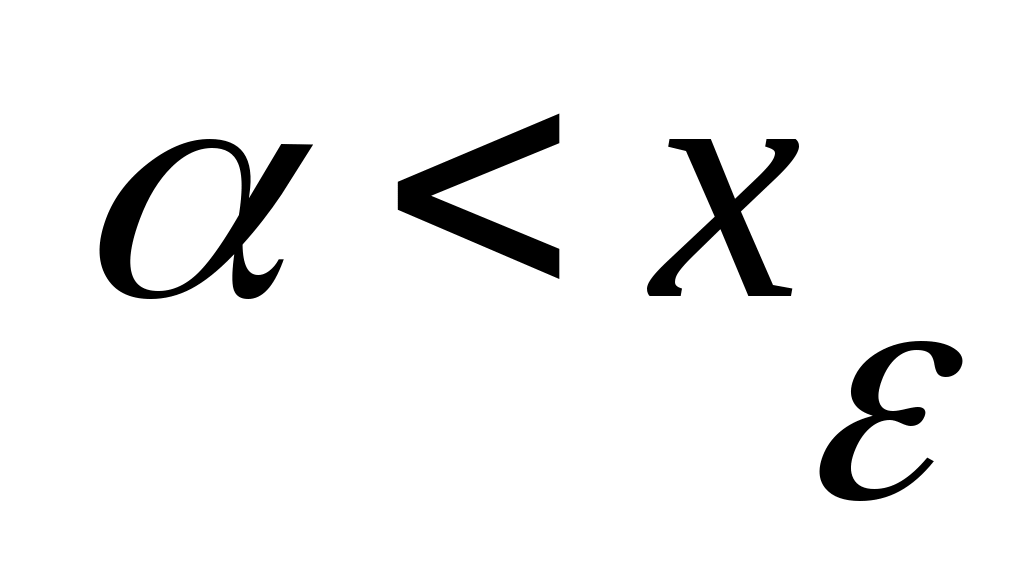
теңсіздігі 1) шартындағы 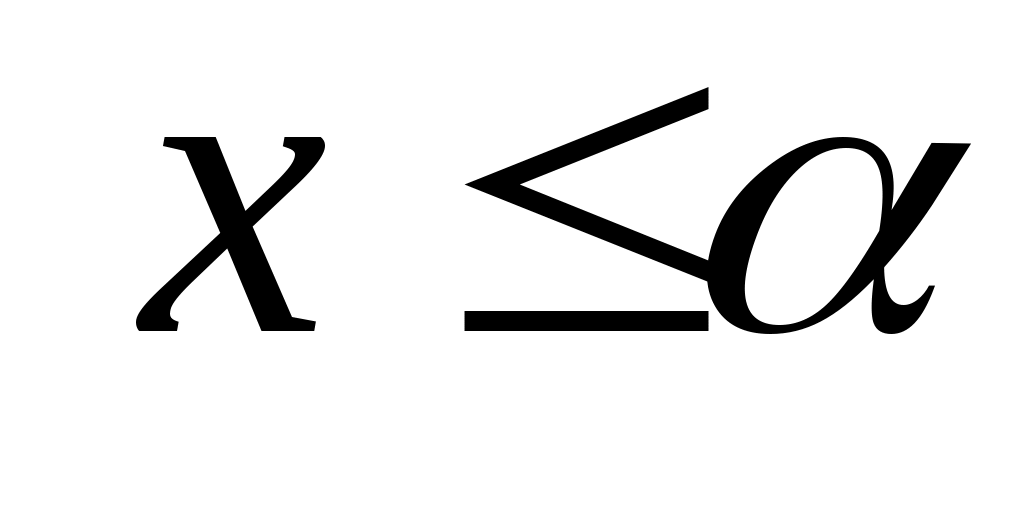 теңсіздігіне қайшы. Ендеше, теңсіздігіне қайшы. Ендеше, 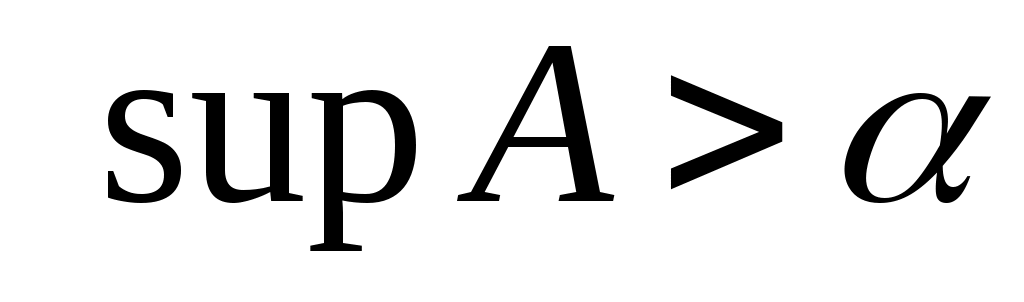
теңсіздігі орындалмайды.
Енді 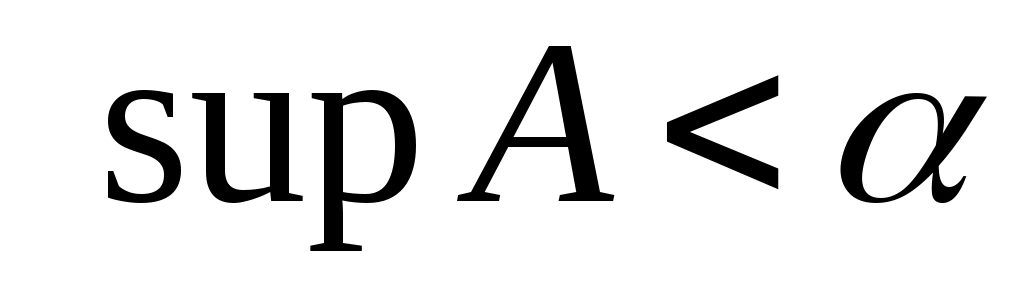 теңсіздігі орындалады деп, 2) шартындағы теңсіздігі орындалады деп, 2) шартындағы 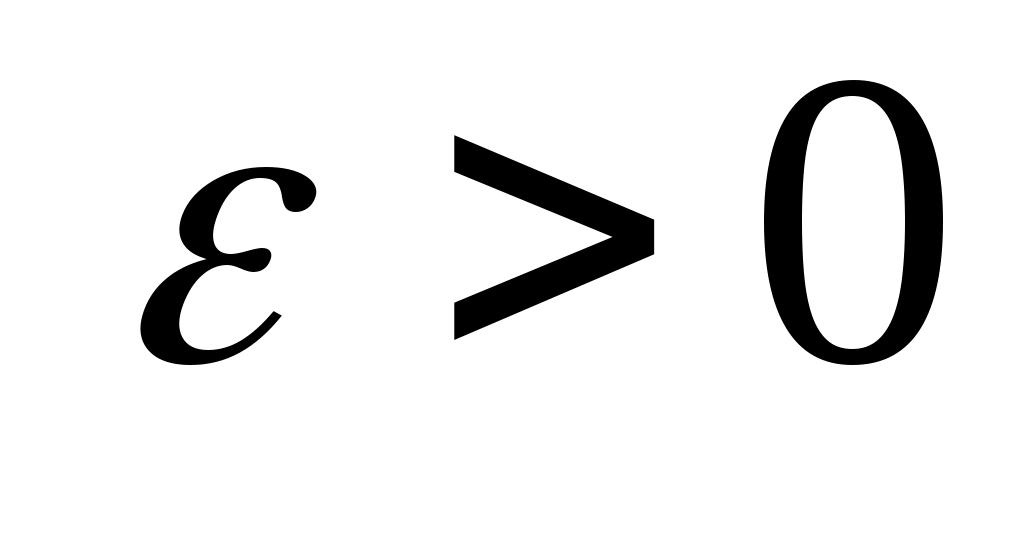 саны ретінде саны ретінде 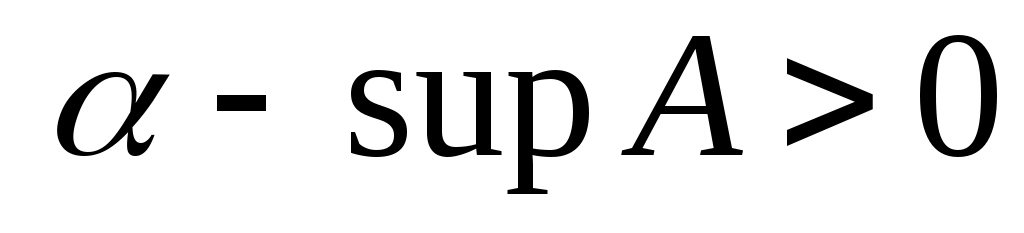 санын алсақ, санын алсақ,
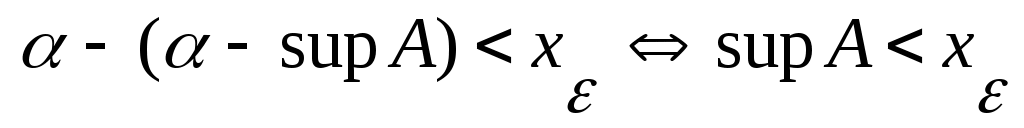
теңсіздігіне келеміз. Бұл теңсіздік  жиынының супремумі анықтамасына қайшы. Демек, жиынының супремумі анықтамасына қайшы. Демек, 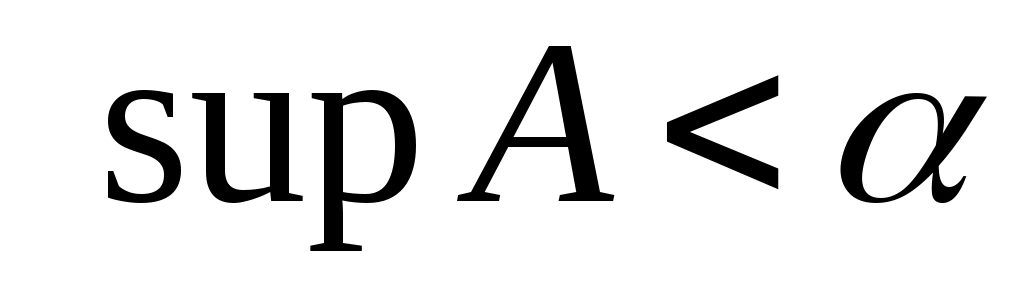 теңсіздігі орындалмайды. Сонымен, теңсіздігі орындалмайды. Сонымен, 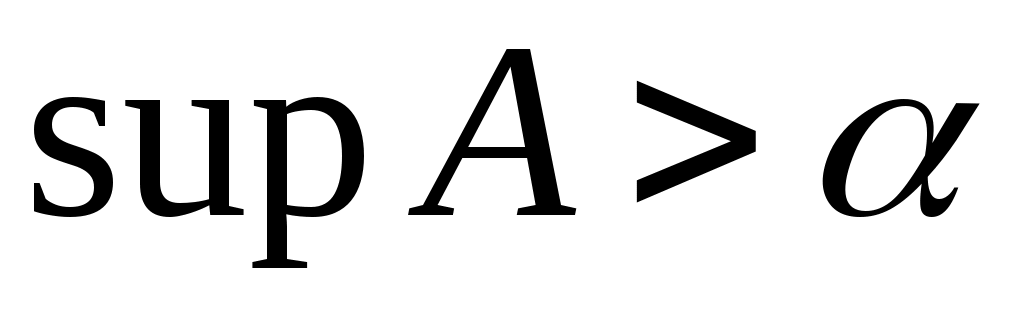 теңсіздігі де, теңсіздігі де, 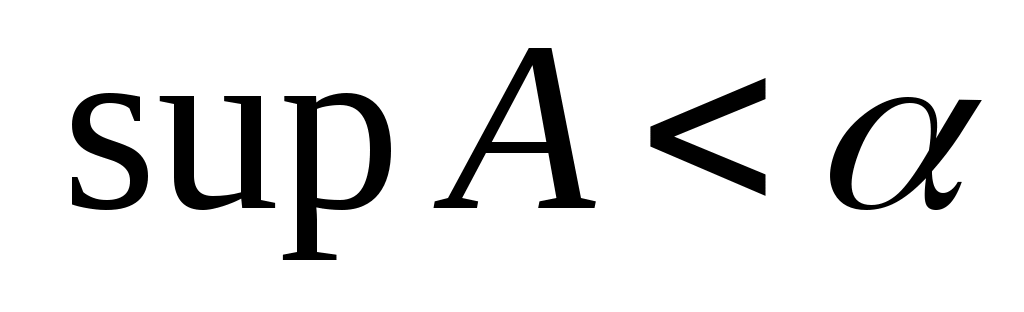 теңсіздігі де орындалмайтынын көрсеттік. теңсіздігі де орындалмайтынын көрсеттік.
Ендеше, 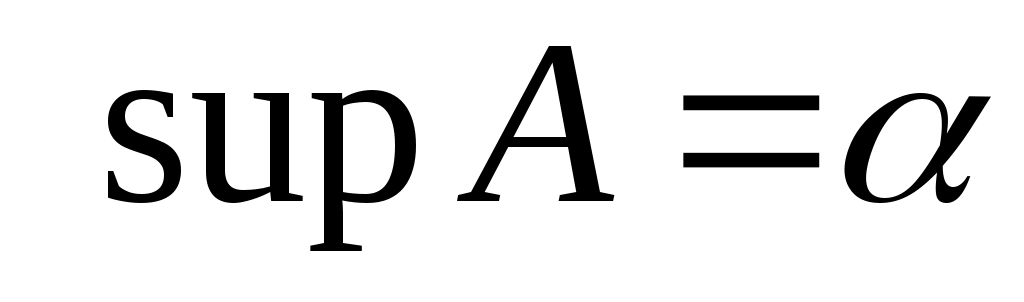 . .
8 – теорема. Егер  жиыны төменненшенелген болса, 1) жиыны төменненшенелген болса, 1) 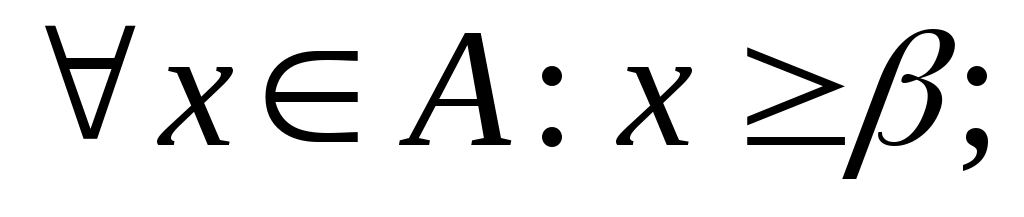 2) 2)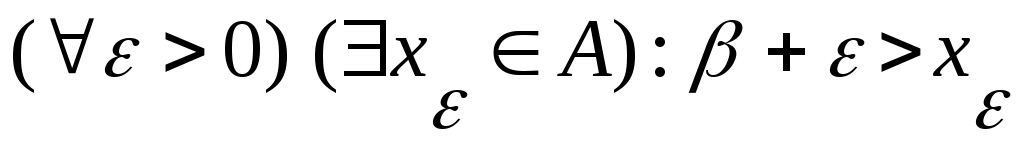 шарттарын қанағаттандыратын шарттарын қанағаттандыратын 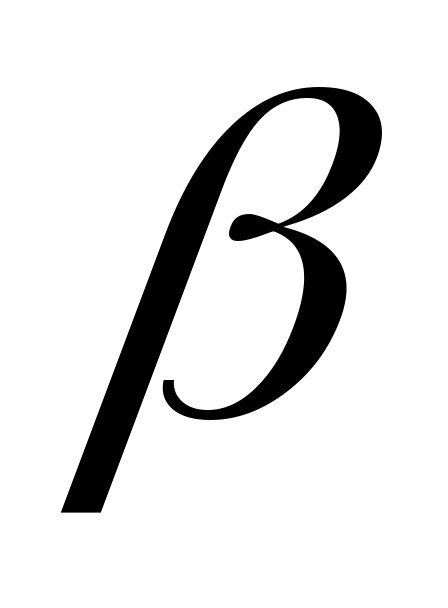 саны саны  жиынының инфимумі жиынының инфимумі 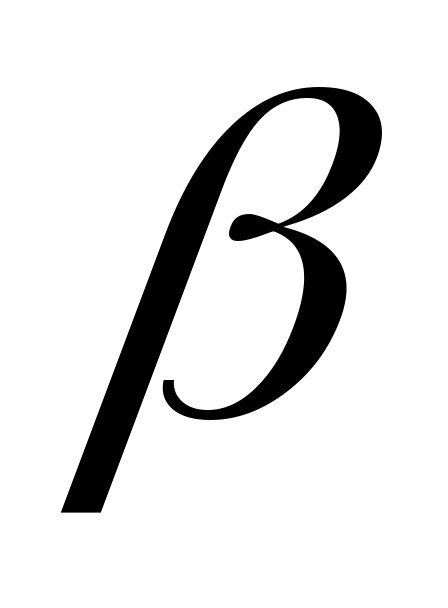 болады. болады.
Дәлелдеуі. 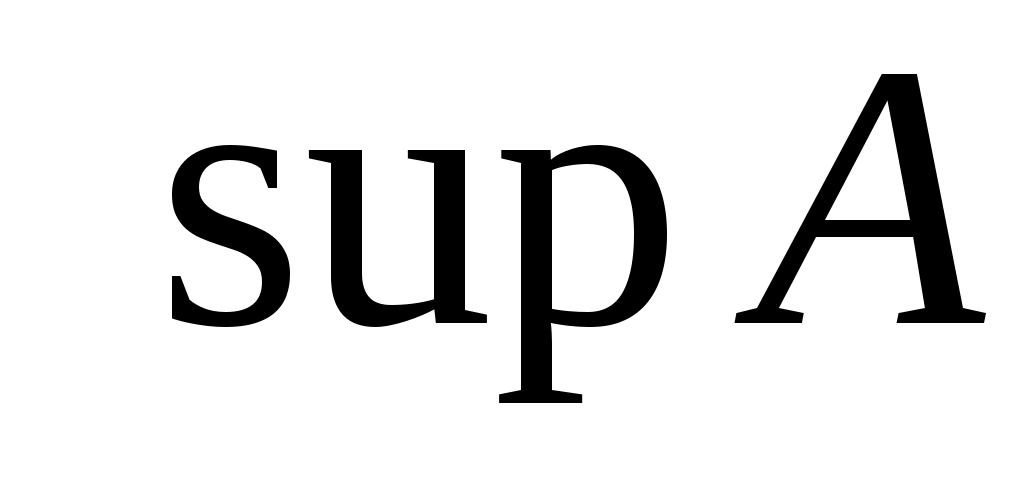 санын санын 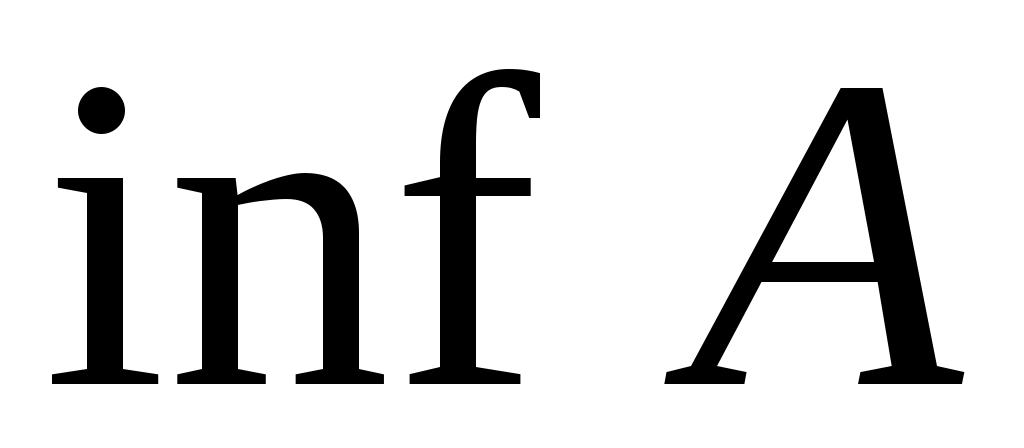 санына, санына,  санын санын 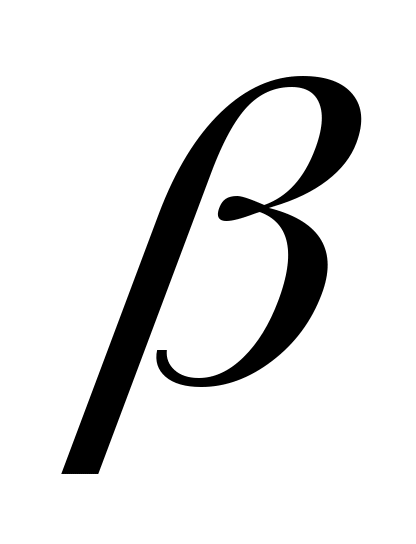 санына алмастырып, 7– теореманы дәлелдеу жолын қайталаймыз. санына алмастырып, 7– теореманы дәлелдеу жолын қайталаймыз.
§2. Эквивалентті жиындар
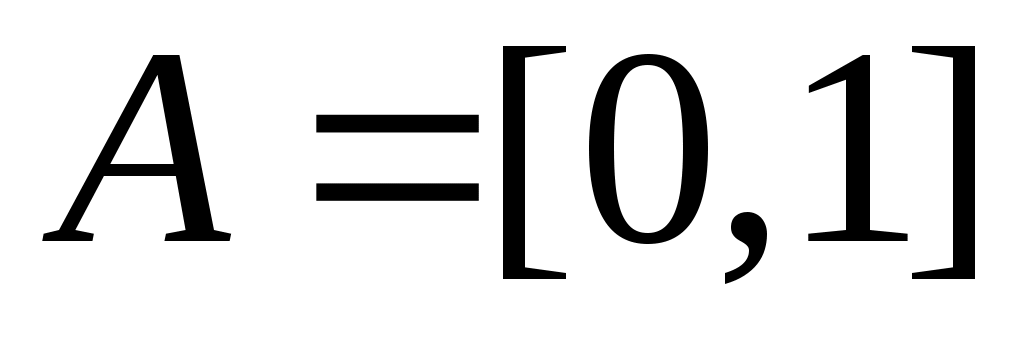 жиынын «ақырсыз көп элементі бар жиын» немесе «ақырсыз көп элементті жиын» (қысқаша: «ақырсыз жиын») деп атауға болады, өйткені, әрбір жиынын «ақырсыз көп элементі бар жиын» немесе «ақырсыз көп элементті жиын» (қысқаша: «ақырсыз жиын») деп атауға болады, өйткені, әрбір 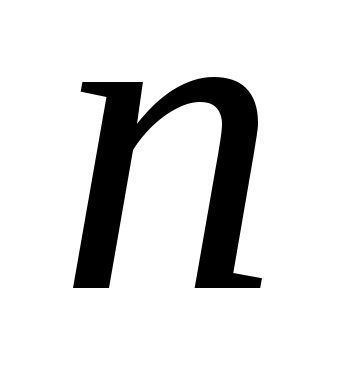 үшін үшін  жиынында жататын жиынында жататын 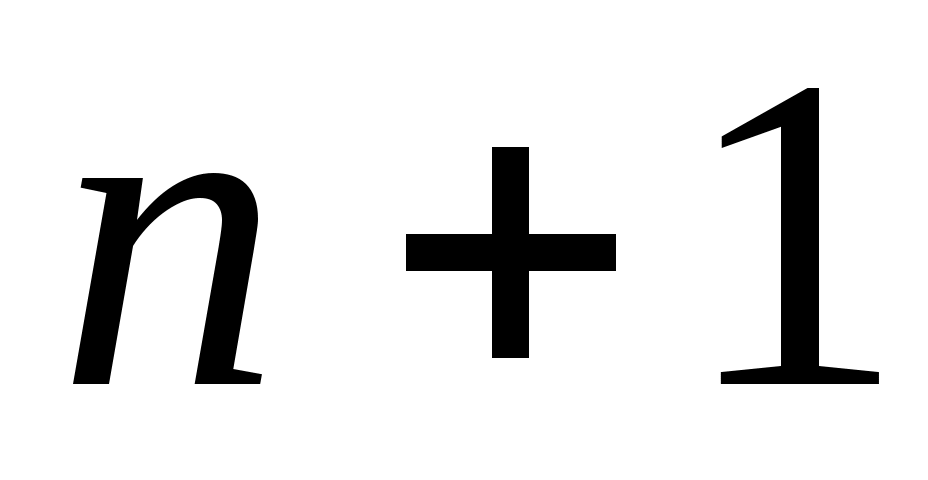 элемент көрсете аламыз. Мысалы, әрбір элемент көрсете аламыз. Мысалы, әрбір 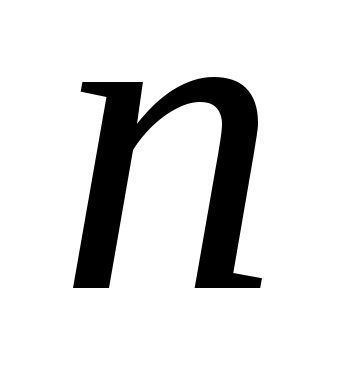 үшін үшін 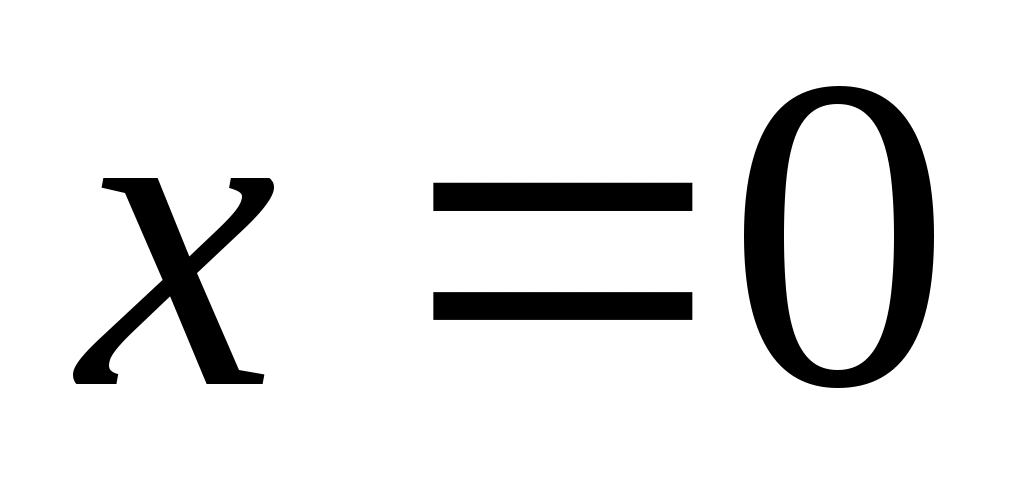 , , 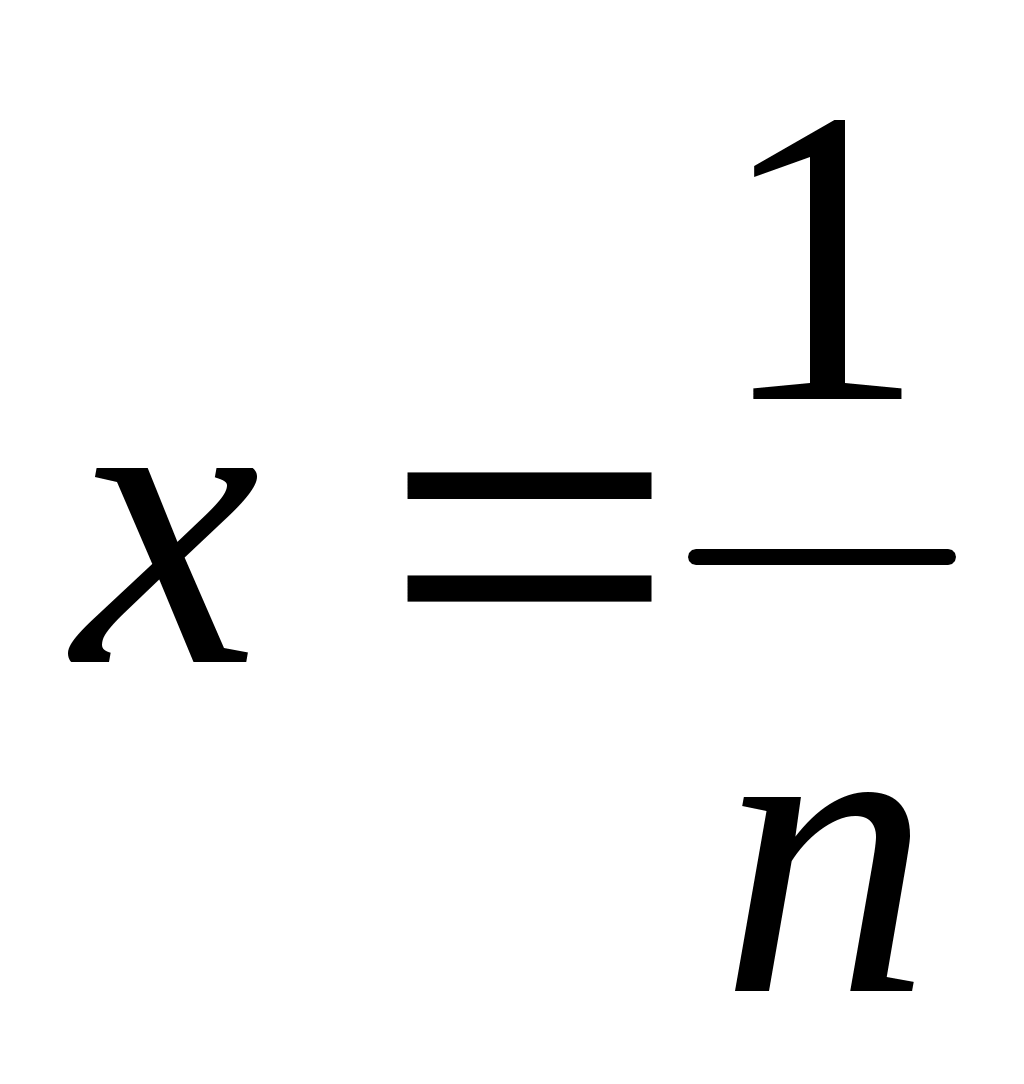 , , 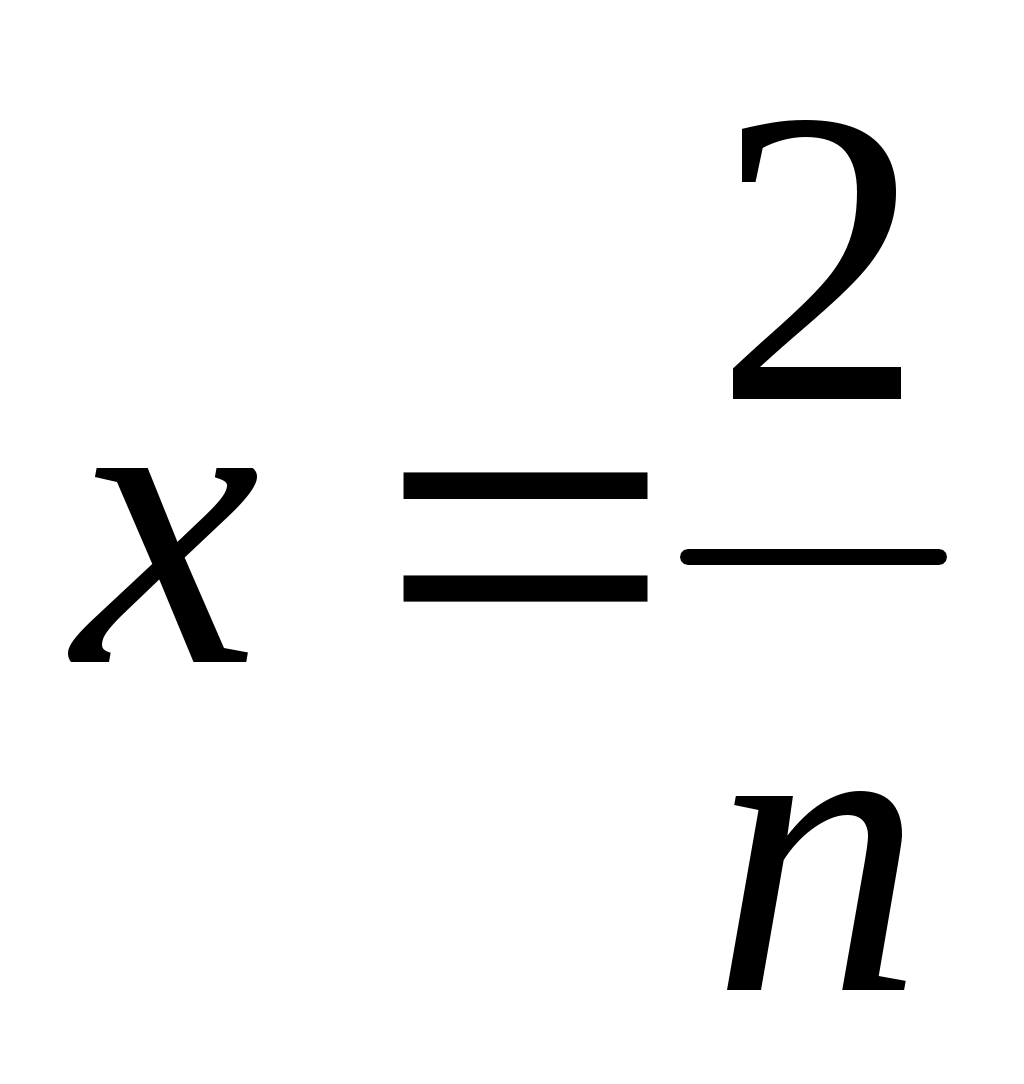 ,..., ,...,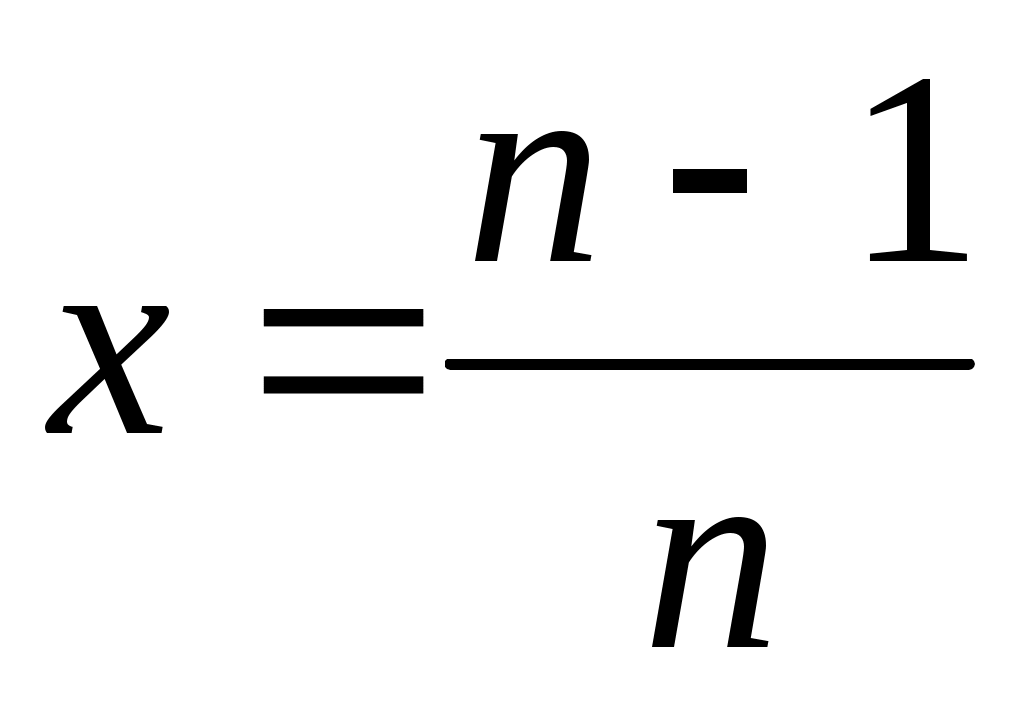 , , 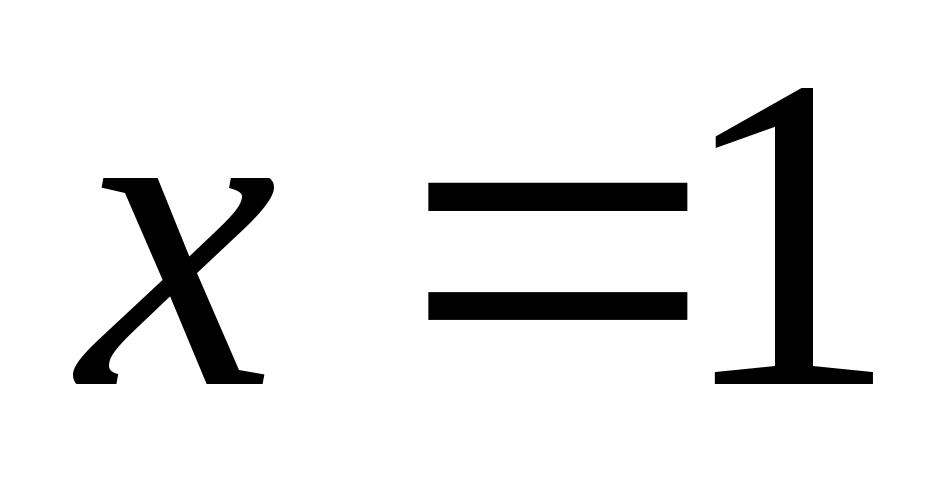 нүктелері нүктелері  жиынында жатады. жиынында жатады. 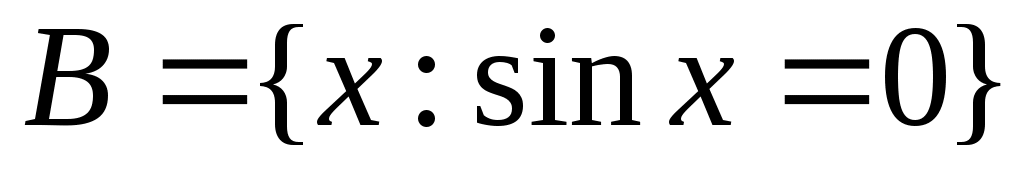 жиынын алсақ та, әрбір жиынын алсақ та, әрбір 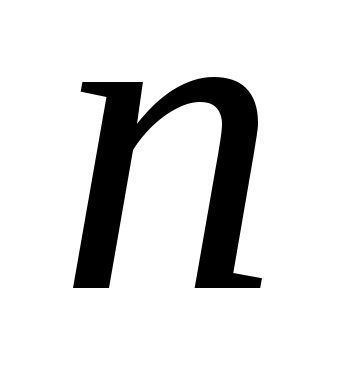 үшін үшін 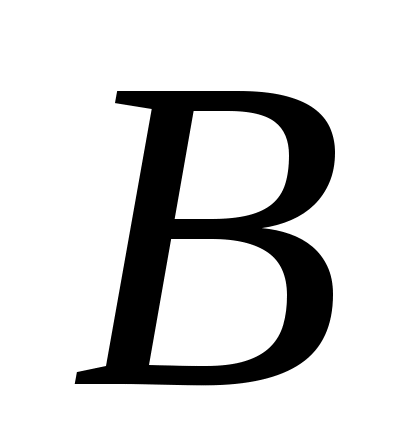 жиынында жататын жиынында жататын 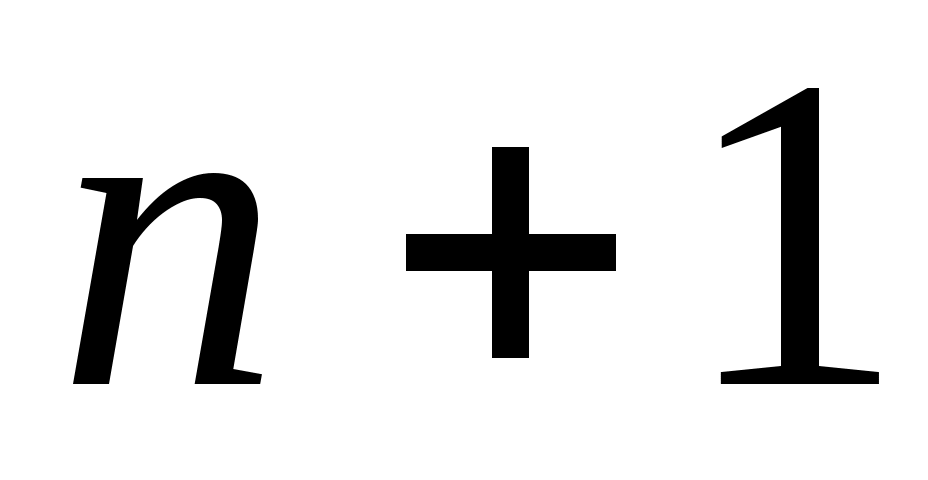 элемент көрсете аламыз: әрбір элемент көрсете аламыз: әрбір 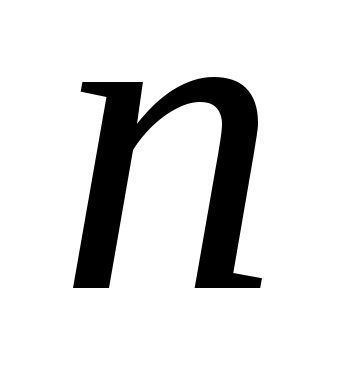 үшін үшін 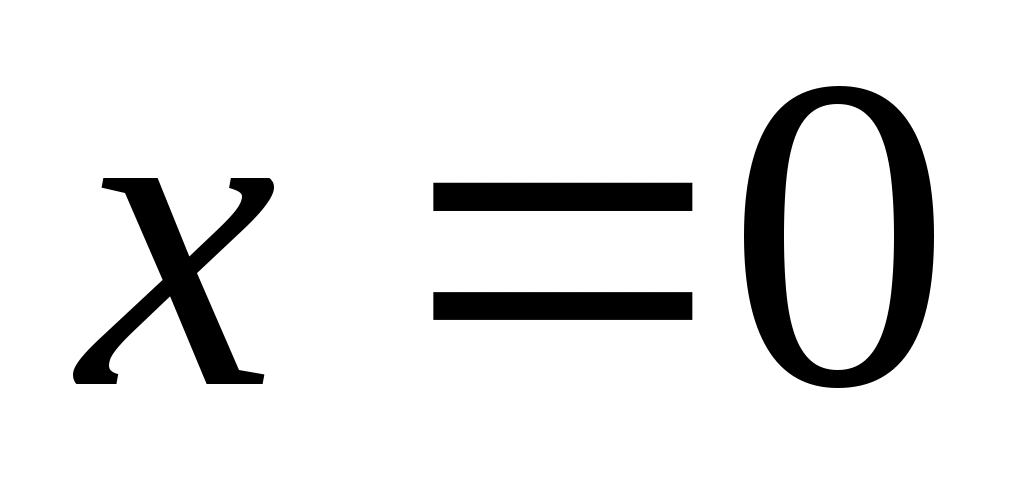 , , 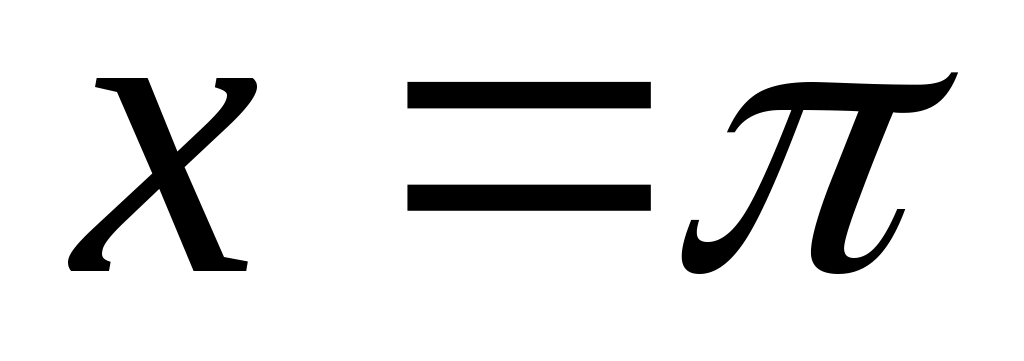 , , 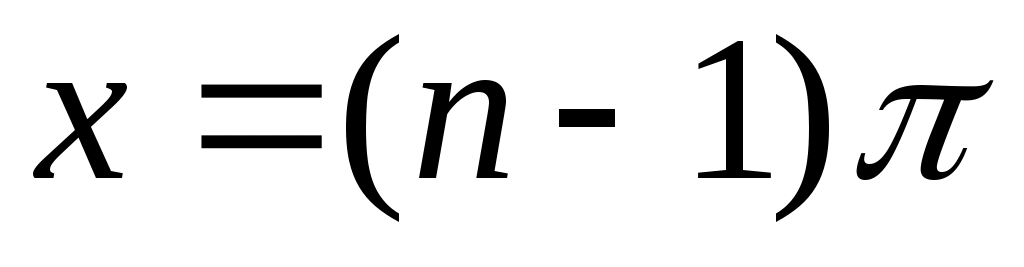 , , 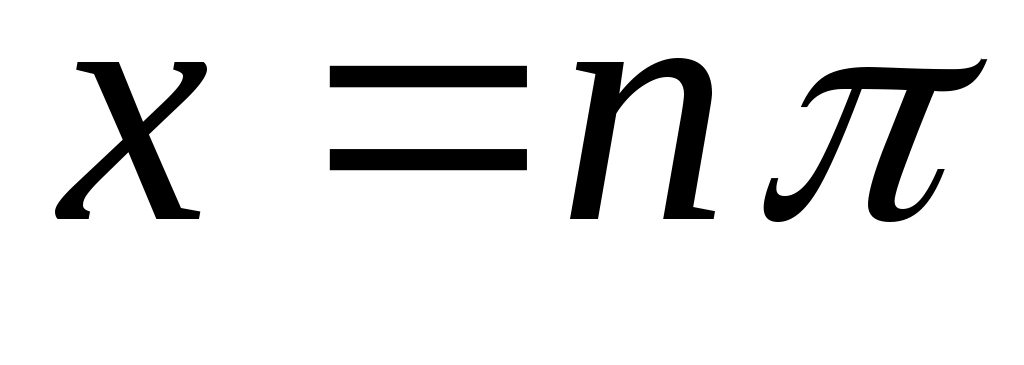 нүктелері нүктелері 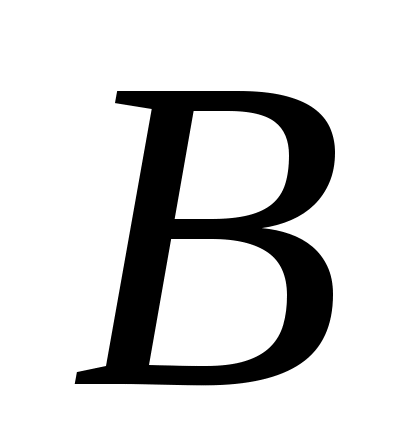 жиынында жатады. Бұдан әрі әрбір жиынында жатады. Бұдан әрі әрбір 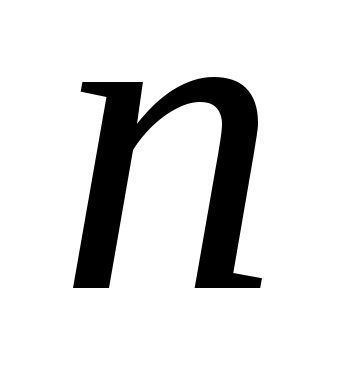 үшін құрамында үшін құрамында 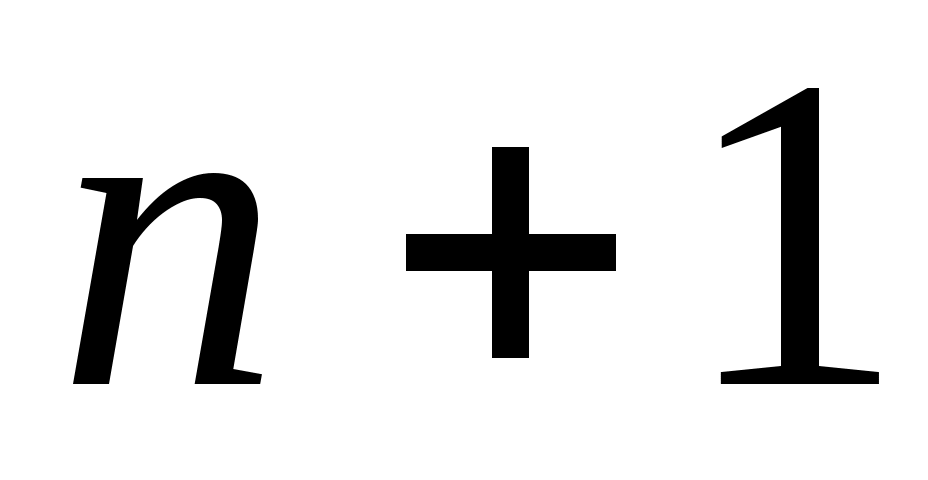 элемент бар болатын жиынды ақырсыз жиын деп атаймыз. Ал ақырсыз емес жиынды ақырлы жиын деп атайтын боламыз. элемент бар болатын жиынды ақырсыз жиын деп атаймыз. Ал ақырсыз емес жиынды ақырлы жиын деп атайтын боламыз.
Әрбір ақырлы жиын үшін «жиынның қанша элементі бар», ал әрбір ақырсыз жиын үшін «жиынның элементтері қаншалықты көп» деген сұрақ қойылады. Қуат сөзін қолданып, «жиынның қанша элементі бар», «жиынның элементтері қаншалықты көп» сұрақтарын ықшам түрде кез келген ақырлы, не ақырсыз жиын үшін «жиынның қуаты қандай?» деп қоюға болады. Неміс математигі Г. Кантор (1845 –1918)  жиынының қуатын жиынының қуатын  символымен белгілеген (қараңыз, [2], 26 – бет). Бұл белгілеу қазіргі кезде де пайдаланылады. Әрине, символымен белгілеген (қараңыз, [2], 26 – бет). Бұл белгілеу қазіргі кезде де пайдаланылады. Әрине, 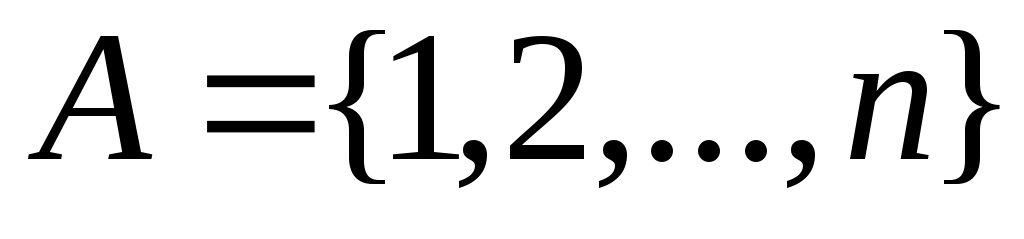 жиыны үшін жиыны үшін 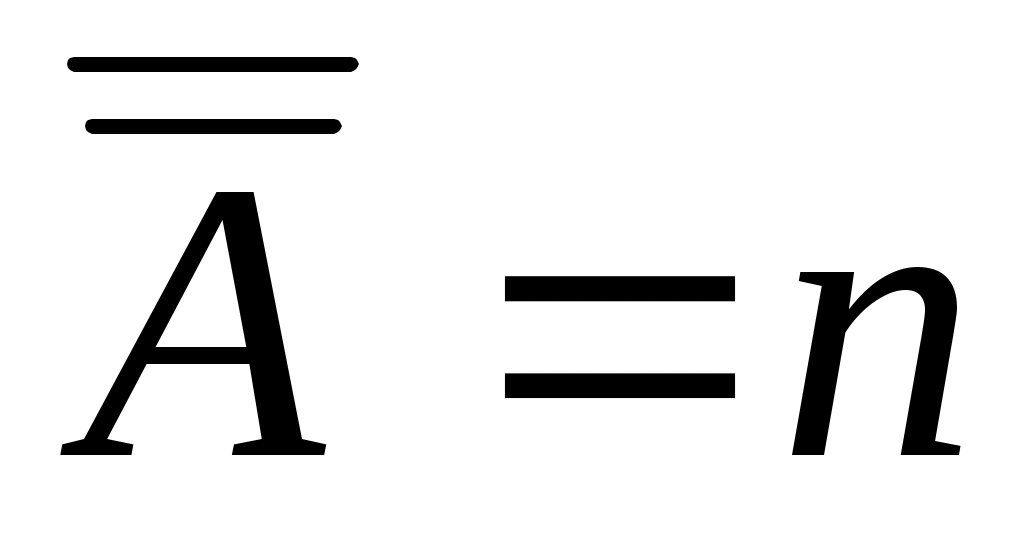 . Натурал сандар жиынының қуатын . Натурал сандар жиынының қуатын  әрпімен, ал нақты сандар жиынының қуатын әрпімен, ал нақты сандар жиынының қуатын 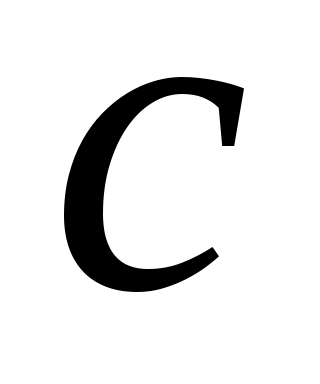 әрпімен белгілеу қалыптасқан. әрпімен белгілеу қалыптасқан.
Кез келген жиынның қуатын анықтау мәселесі «эквивалентті жиындар» ұғымы арқылы шешіледі
 жиынының әртүрлі элементтеріне жиынының әртүрлі элементтеріне 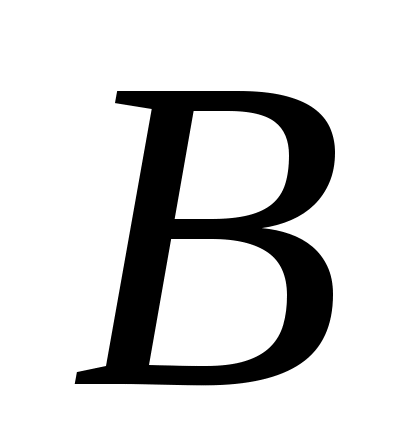 жиынының әртүрлі элементтерін сәйкес қоятын және жиынының әртүрлі элементтерін сәйкес қоятын және 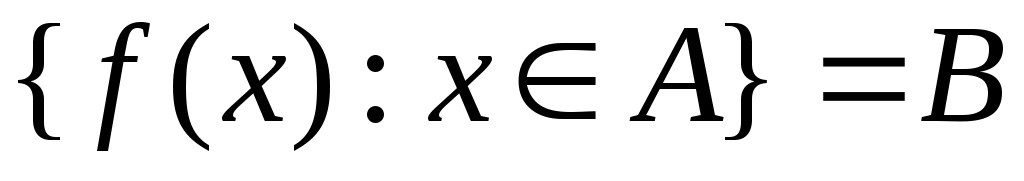 теңдігін қанағаттандыратын әрбір теңдігін қанағаттандыратын әрбір 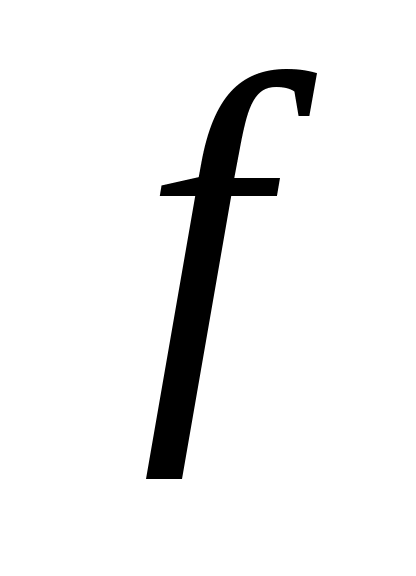 функциясы функциясы  және және 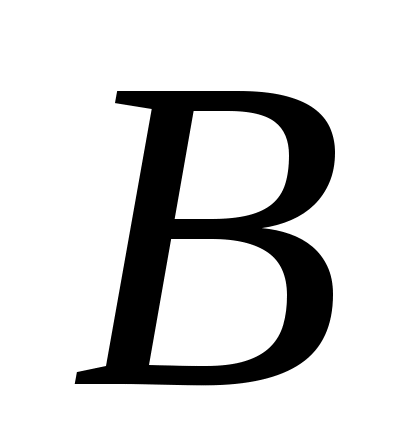 жиындары арасында өзара бірмәнді сәйкестік орнатады. Яғни, жиындары арасында өзара бірмәнді сәйкестік орнатады. Яғни,  жиынының әрбір элементіне жиынының әрбір элементіне 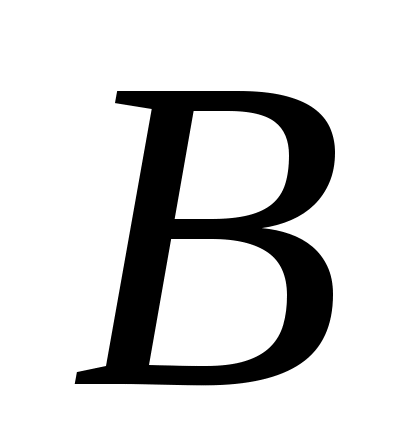 жиынының бір элементі және керісінше, жиынының бір элементі және керісінше, 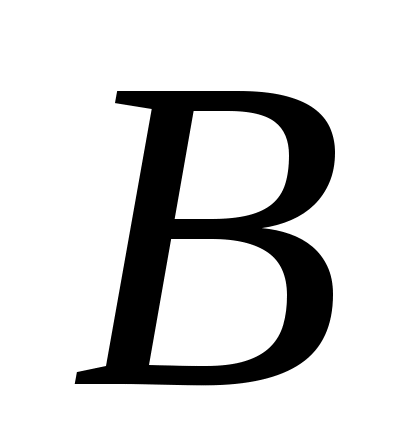 жиынының әрбір элементіне жиынының әрбір элементіне жиынының бір элементі сәйкес қойылады. жиынының бір элементі сәйкес қойылады.
Анықтама. Арасында өзара бірмәнді сәйкестік орнатылған жиындарды эквивалентті жиындар деп атаймыз.
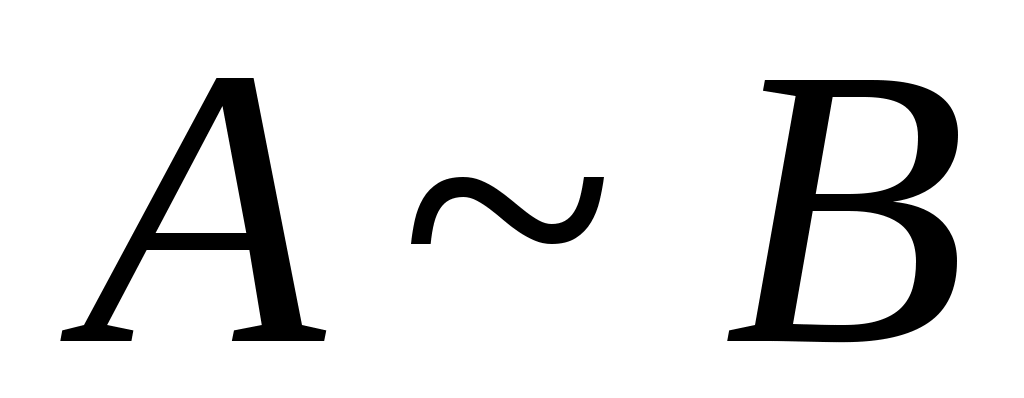 жазуы жазуы  және және 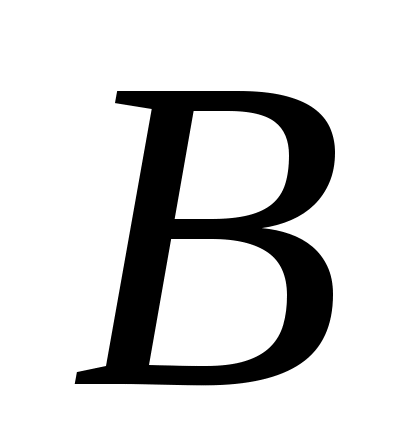 жиындарының эквивалентті жиындар екенін білдіреді. жиындарының эквивалентті жиындар екенін білдіреді.
Мысал. 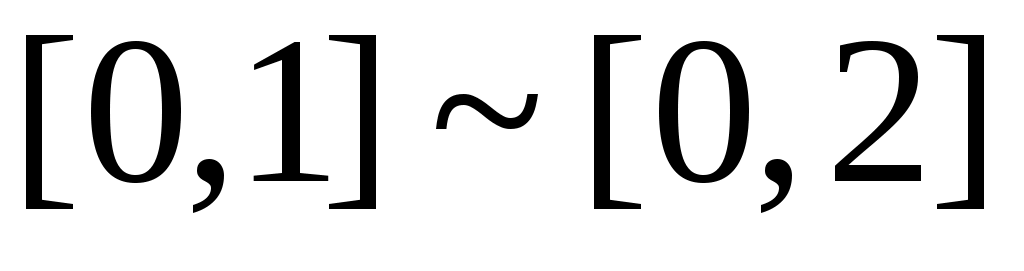 , өйткені, , өйткені, 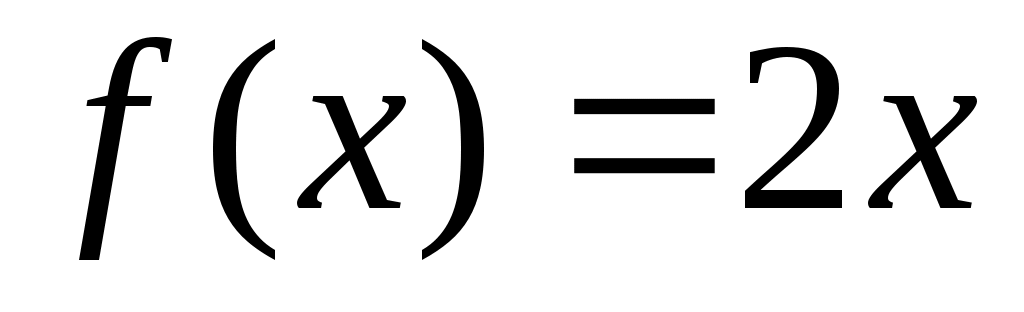 теңдігі бойынша анықталған теңдігі бойынша анықталған 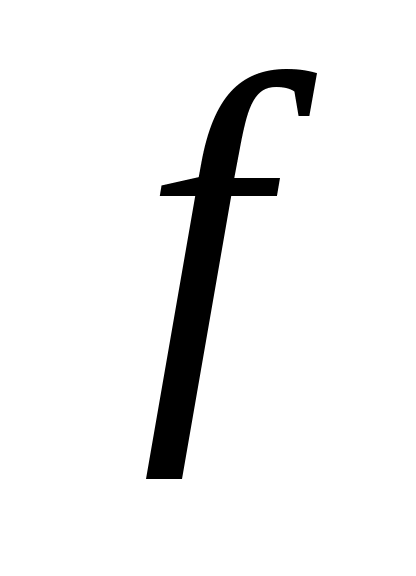 функциясы функциясы 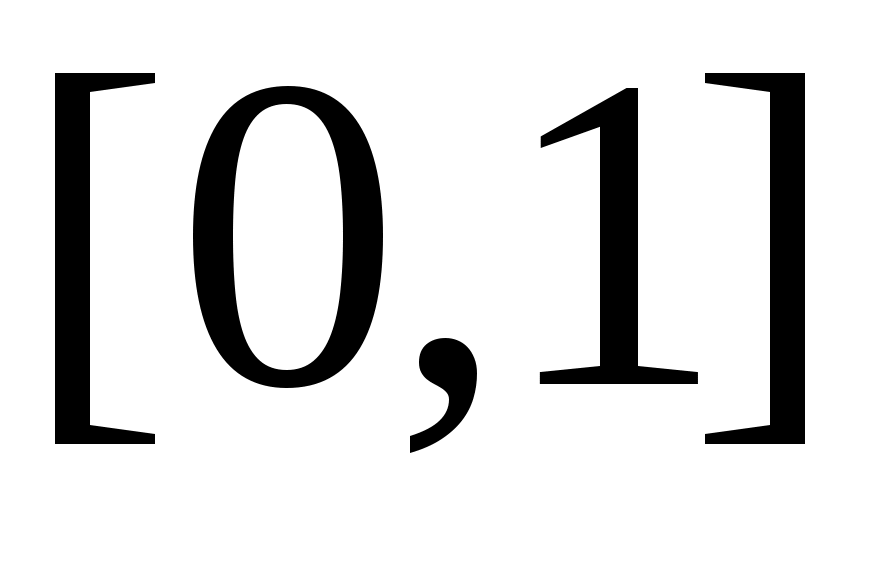 және және 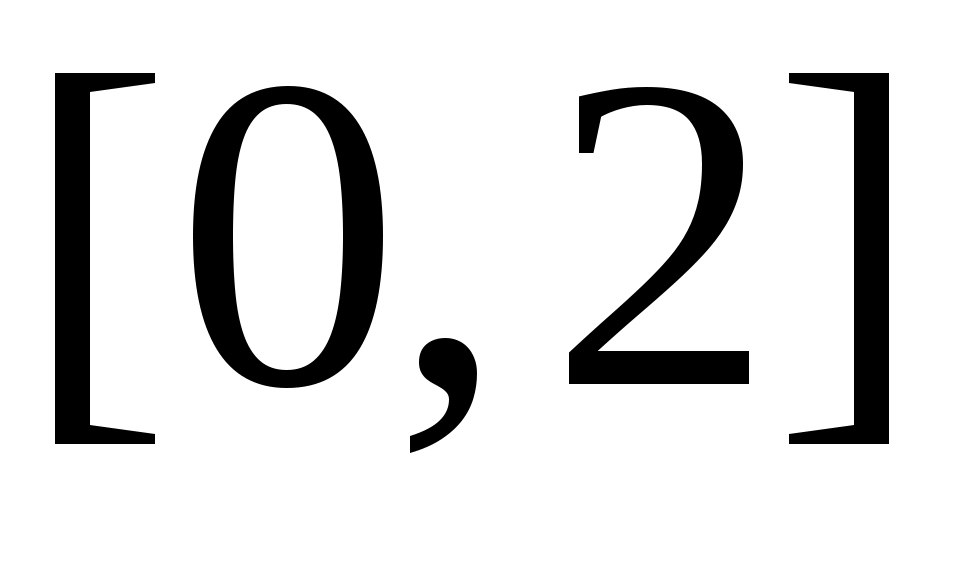 жиындары арасында өзара бірмәнді сәйкестік орнатады. жиындары арасында өзара бірмәнді сәйкестік орнатады.
Эквивалентті жиындардың бірінде қанша элемент болса, екіншісінде сонша элемент бар болады. Сондықтан эквивалентті жиындарды «қуаттары бірдей (тең) жиындар» немесе «теңқуатты жиындар» деп те атайды.
Енді « жиынының қуаты қандай ?» деген сұраққа былай жауап береміз: жиынының қуаты қандай ?» деген сұраққа былай жауап береміз:
1) Егер  және және 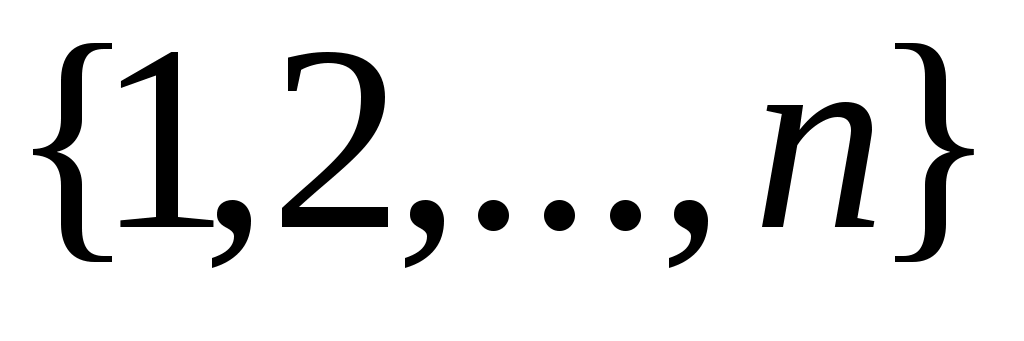 жиындары эквивалентті жиындар болса, онда жиындары эквивалентті жиындар болса, онда
« жиынының қуаты жиынының қуаты 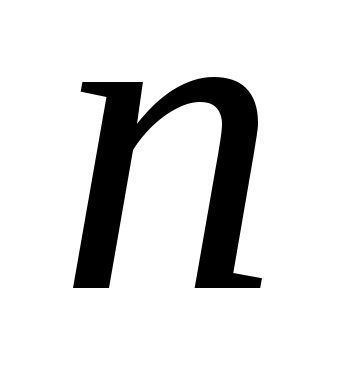 – ге тең» дейміз; – ге тең» дейміз;
2) Егер  және және 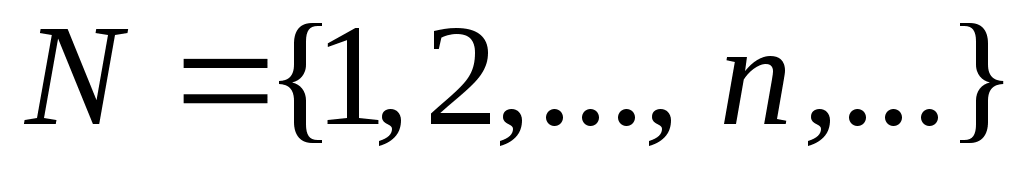 жиындары эквивалентті жиындар болса, онда « жиындары эквивалентті жиындар болса, онда « жиынының қуаты жиынының қуаты  » дейміз; » дейміз;
3) Егер  және және 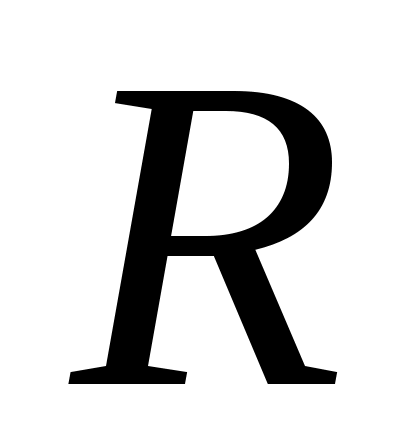 жиындары эквивалентті жиындар болса, онда « жиындары эквивалентті жиындар болса, онда « жиынының қуаты континуум» (қысқаша: « жиынының қуаты континуум» (қысқаша: « жиынының қуаты жиынының қуаты 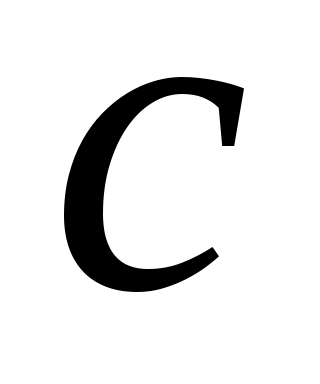 ») дейміз. ») дейміз.
Ал  және және  , ,  және және 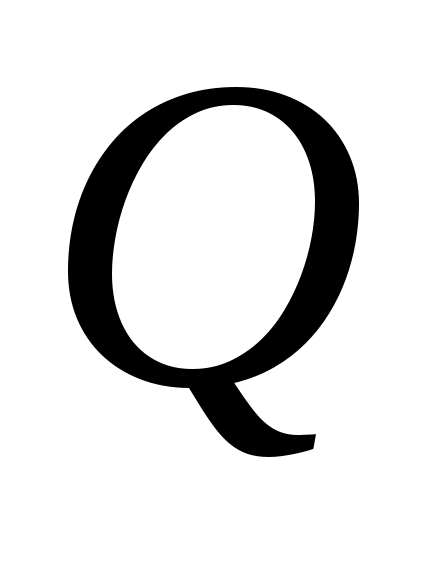 жиындары арасындағы өзара бірмәнді сәйкестіктер жиындары арасындағы өзара бірмәнді сәйкестіктер  жиынының элементтері қаншалықты көп екені туралы жаңа мәлімет бермейді, өйткені, жиынының элементтері қаншалықты көп екені туралы жаңа мәлімет бермейді, өйткені, 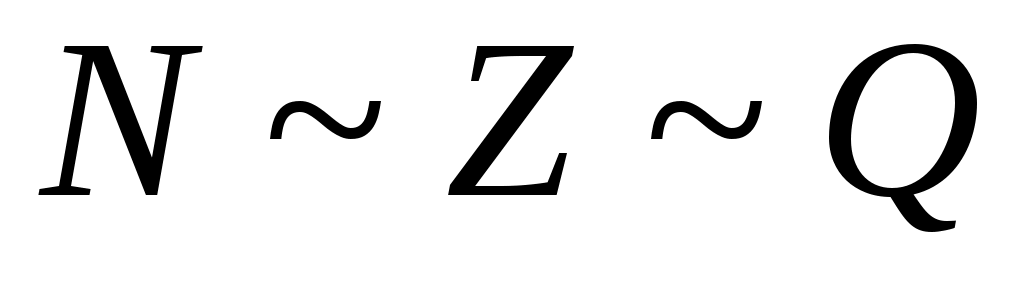 (келесі параграфтағы мысалды және 10 – теореманы қараңыз.). (келесі параграфтағы мысалды және 10 – теореманы қараңыз.).
Қуаты  ( (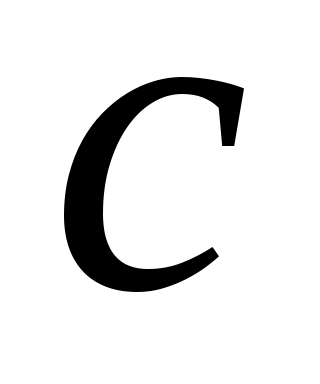 ) жиынды саналымды (континуалды) жиын деп те атайды. «Әрбір ақырсыз жиын не саналымды, не континуалды жиын болады» деп қателікке ұрынбау керек ( 4 – параграфтағы 7– теореманы қараңыз.). ) жиынды саналымды (континуалды) жиын деп те атайды. «Әрбір ақырсыз жиын не саналымды, не континуалды жиын болады» деп қателікке ұрынбау керек ( 4 – параграфтағы 7– теореманы қараңыз.).
Енді эквивалентті жиындардың алдағы материалдарды баяндауда қажет болатын қасиеттерін келтірейік.
1 – теорема. Егер 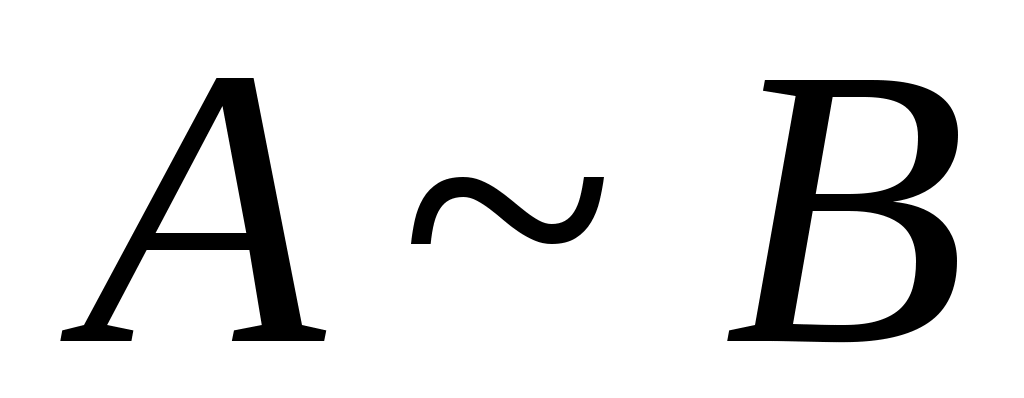 және және 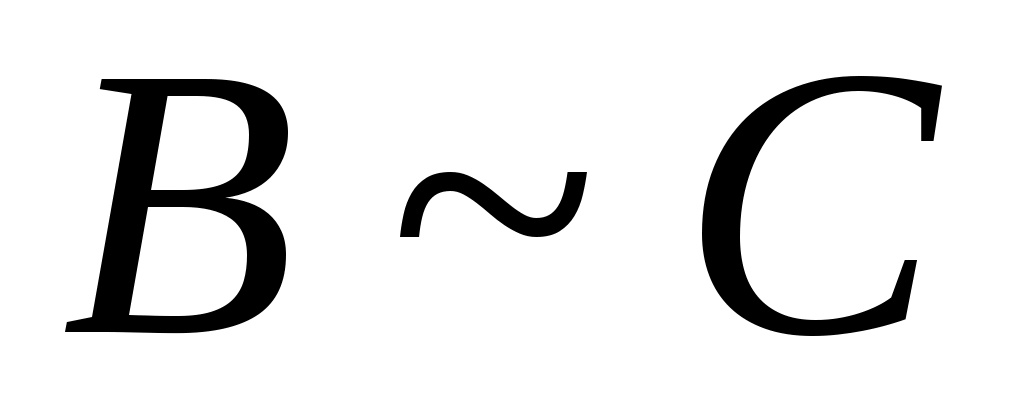 болса, онда болса, онда 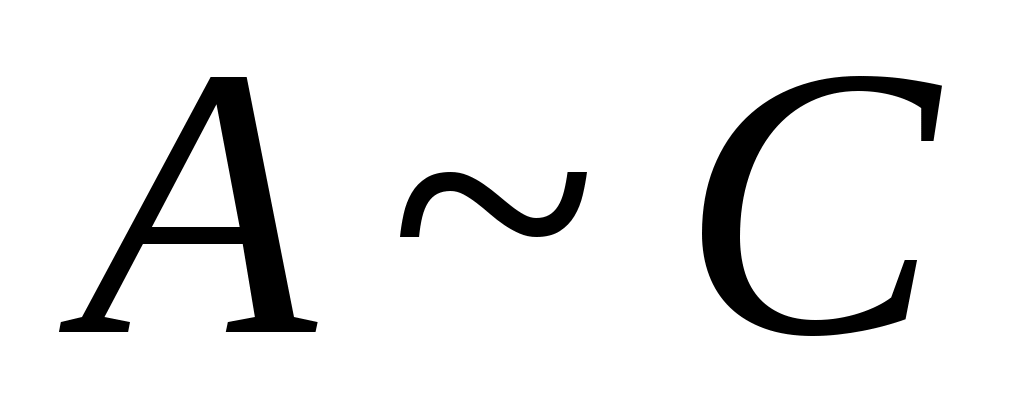 болады. болады.
Дәлелдеуі. 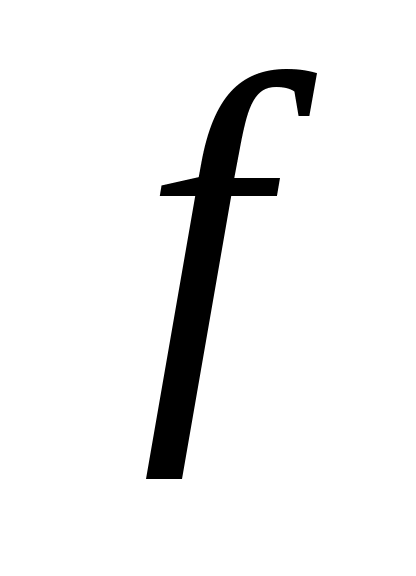 арқылы арқылы 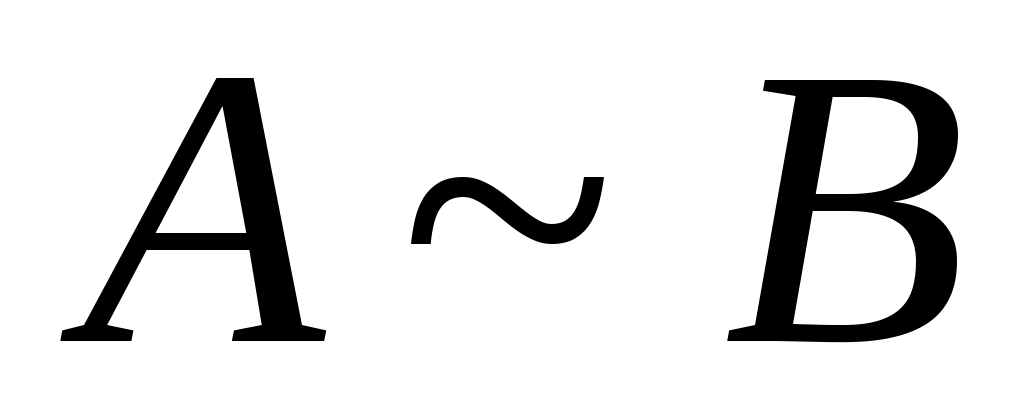 эквиваленттілігін, ал эквиваленттілігін, ал 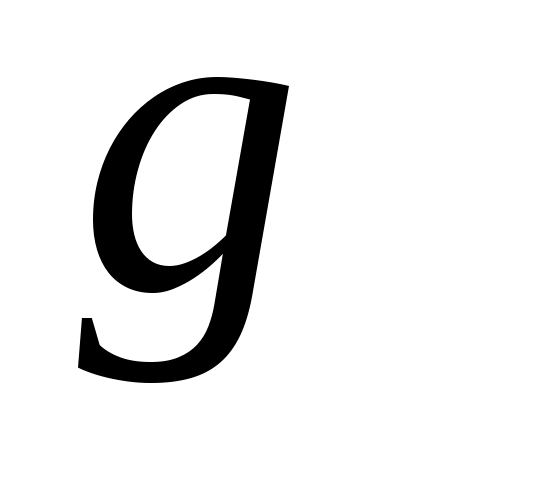 арқылы арқылы 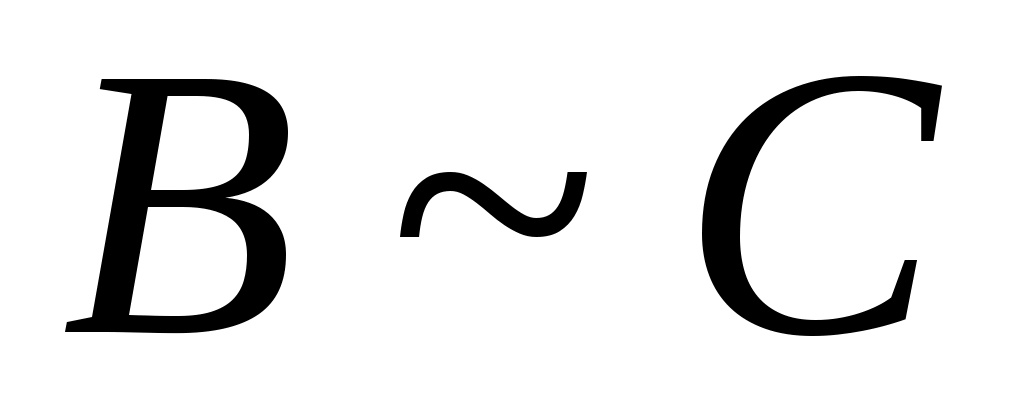 эквиваленттілігін беретін функцияларды белгілесек, онда әрбір эквиваленттілігін беретін функцияларды белгілесек, онда әрбір  элементіне элементіне 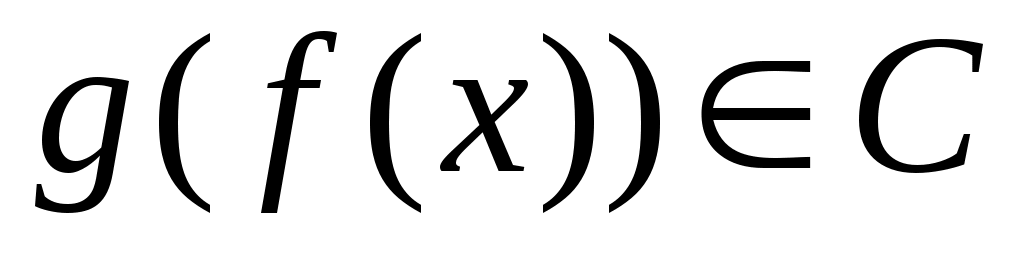 элементін сәйкес қоятын элементін сәйкес қоятын 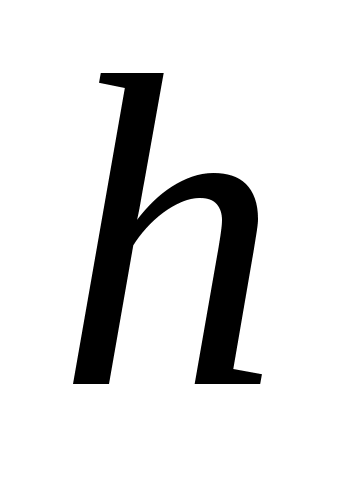 функциясы функциясы  және және 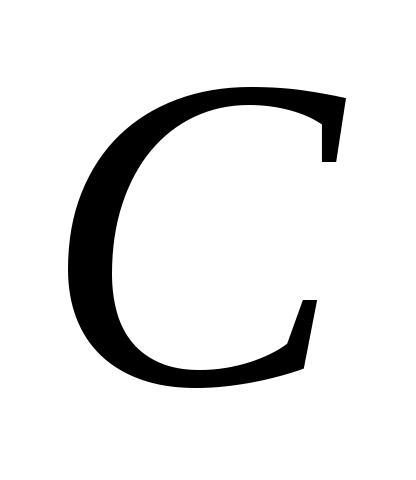 жиындары арасында өзара бірмәнді сәйкестік орнатады. Ендеше, ( жиындары арасында өзара бірмәнді сәйкестік орнатады. Ендеше, (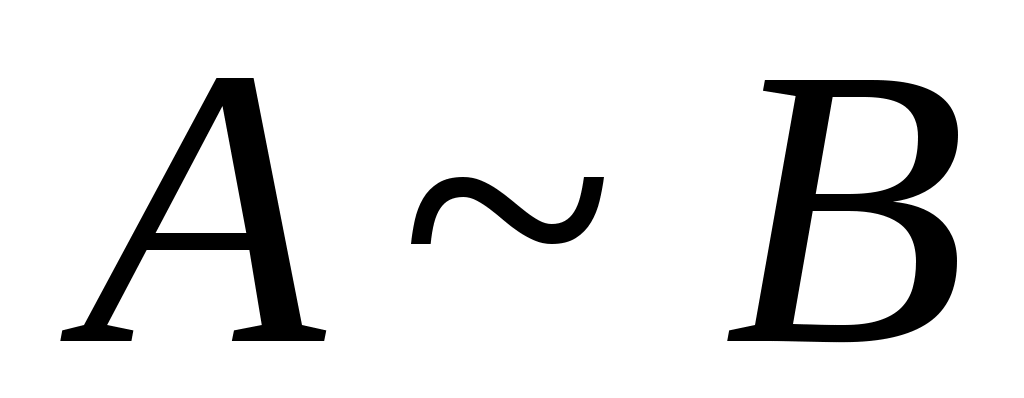 және және 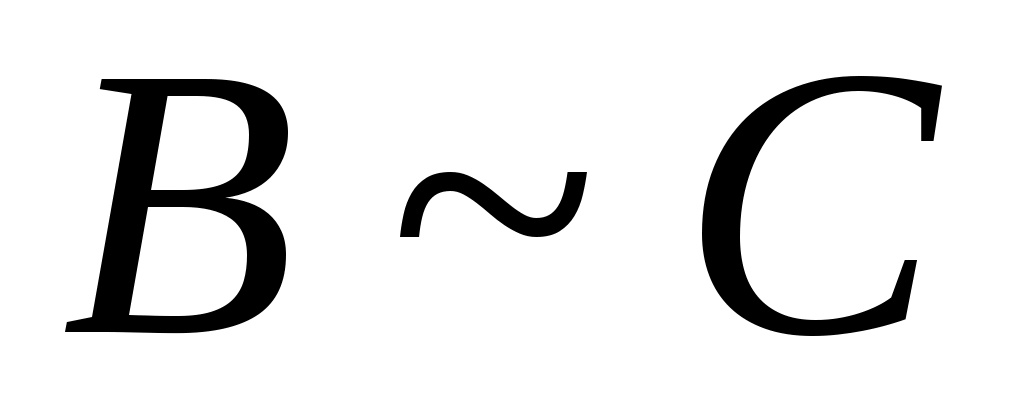 ) ) 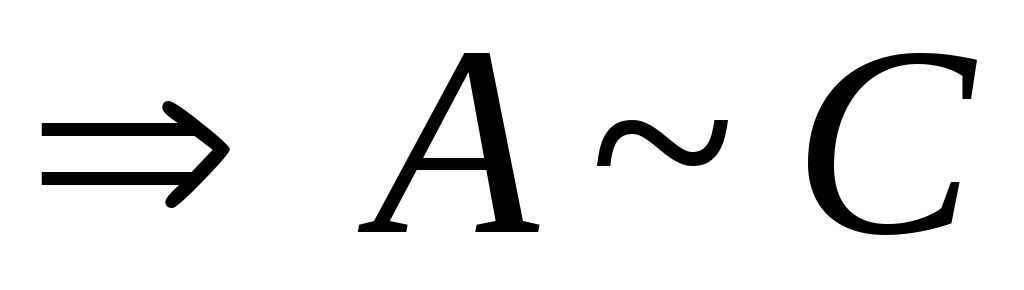 . .
Егер әрбір 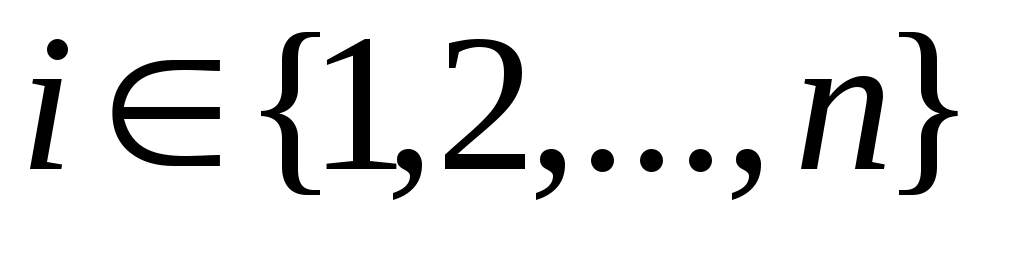 нөміріне нөміріне 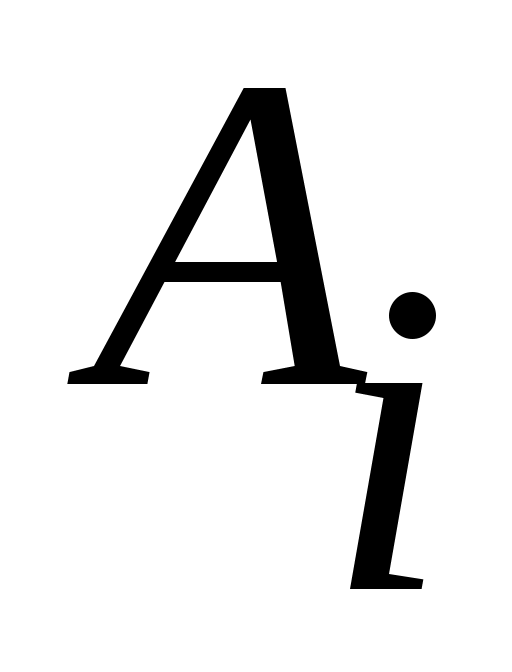 жиыны сәйкес қойылған болса, онда жиыны сәйкес қойылған болса, онда 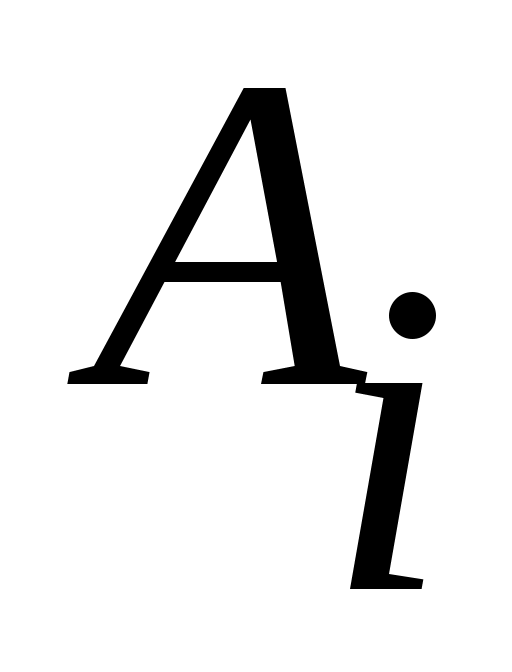 жиындарының кемінде бірінде жататын (әрқайсысында жататын) элементтер жиынын жиындарының кемінде бірінде жататын (әрқайсысында жататын) элементтер жиынын 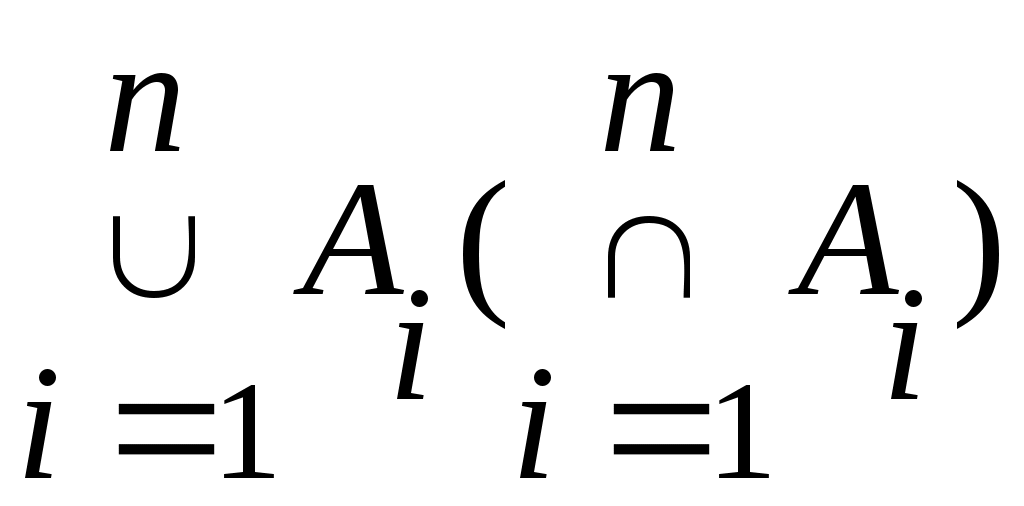 символы арқылы белгілеп, « символы арқылы белгілеп, «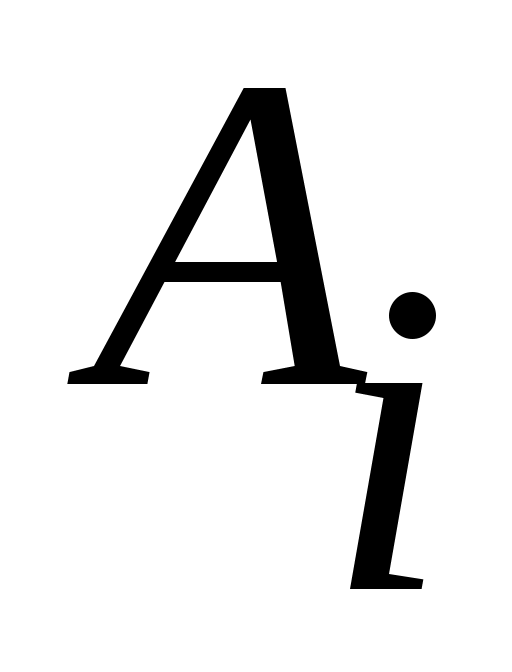 жиындарының ақырлы бірігуі (қиылысуы)» деп айтамыз. жиындарының ақырлы бірігуі (қиылысуы)» деп айтамыз.
Егер әрбір 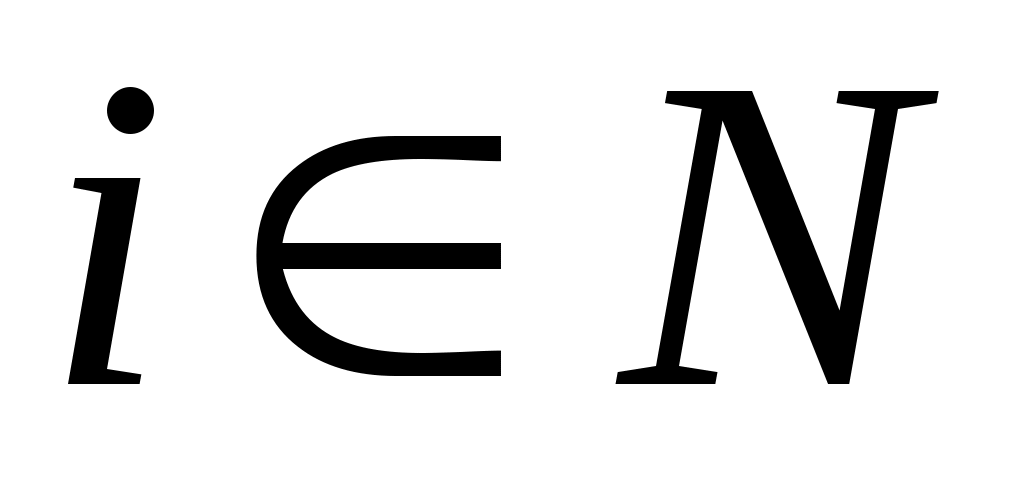 нөміріне нөміріне 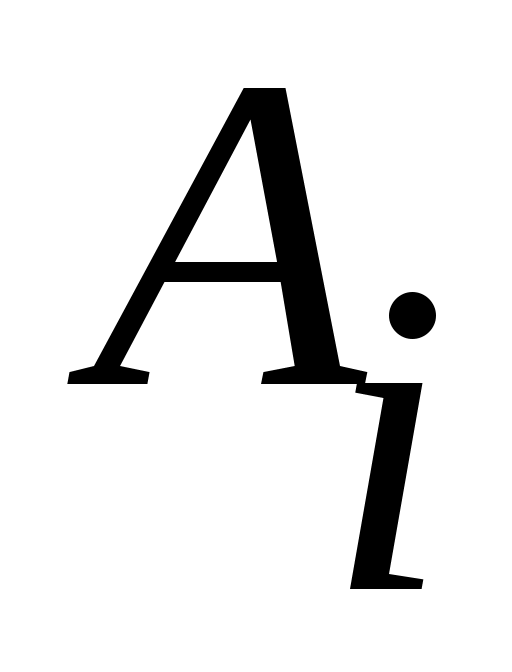 жиыны сәйкес қойылған болса, онда жиыны сәйкес қойылған болса, онда 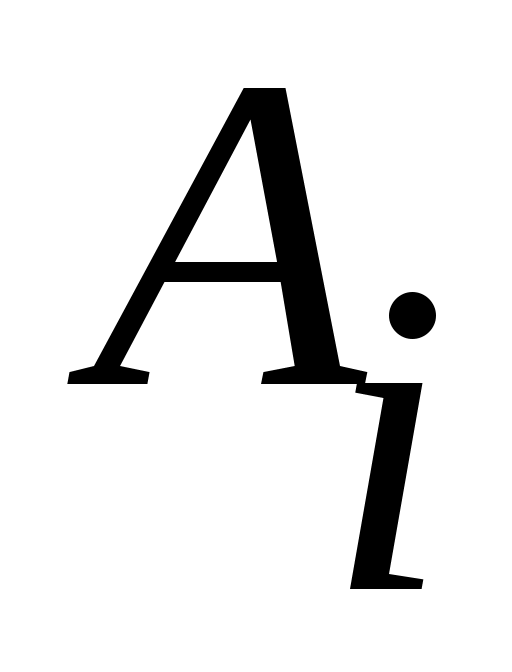 жиындарының кемінде бірінде жататын (әрқайсысында жататын) элементтер жиынын жиындарының кемінде бірінде жататын (әрқайсысында жататын) элементтер жиынын 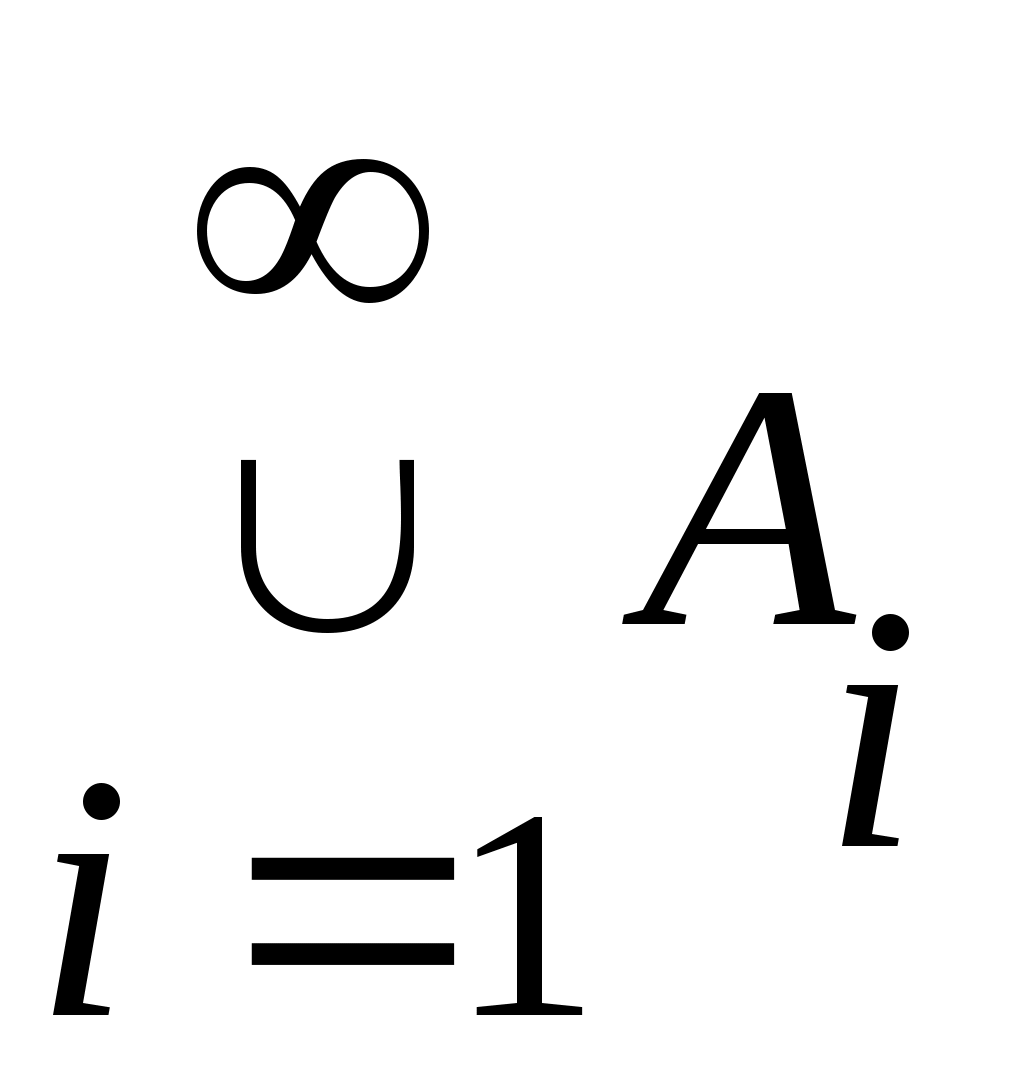 ( (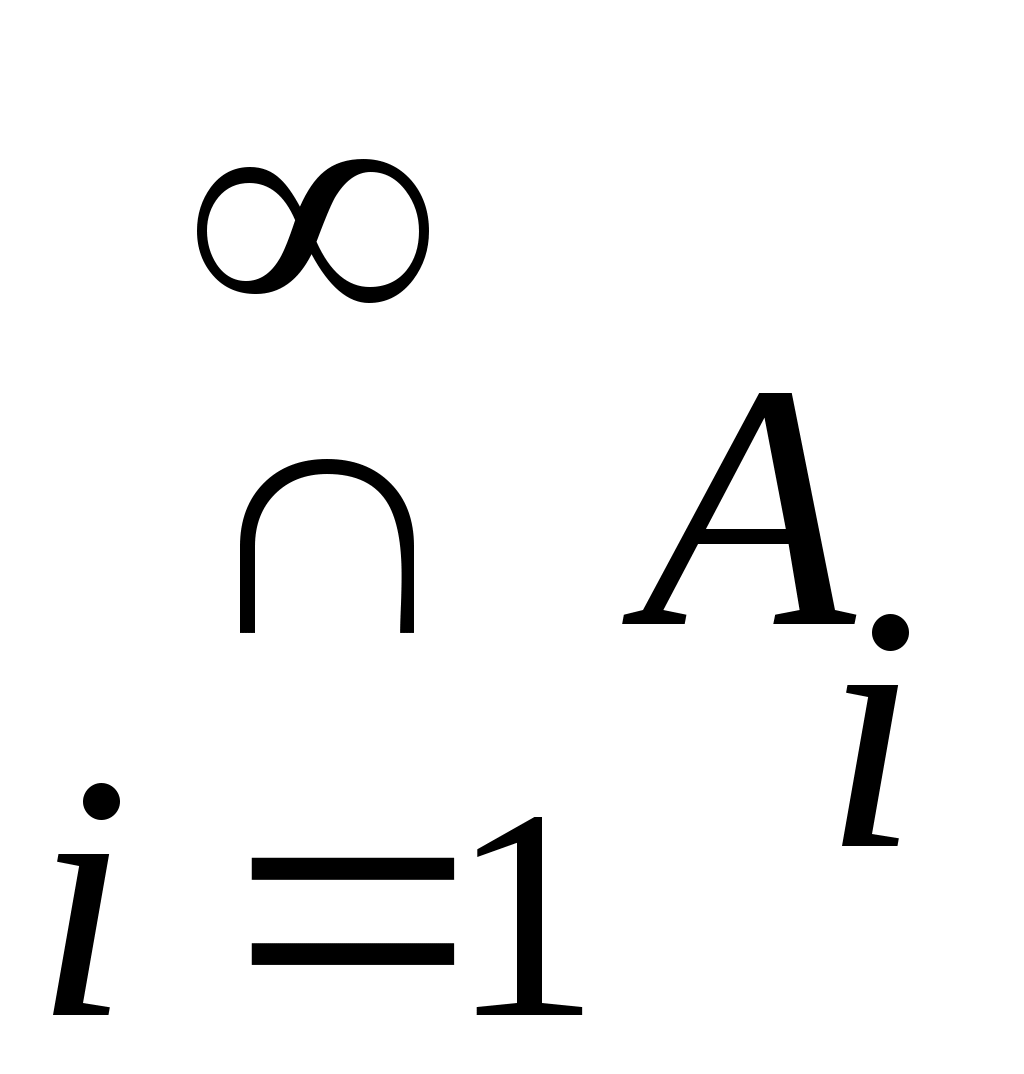 ) символы арқылы белгілеп, « ) символы арқылы белгілеп, «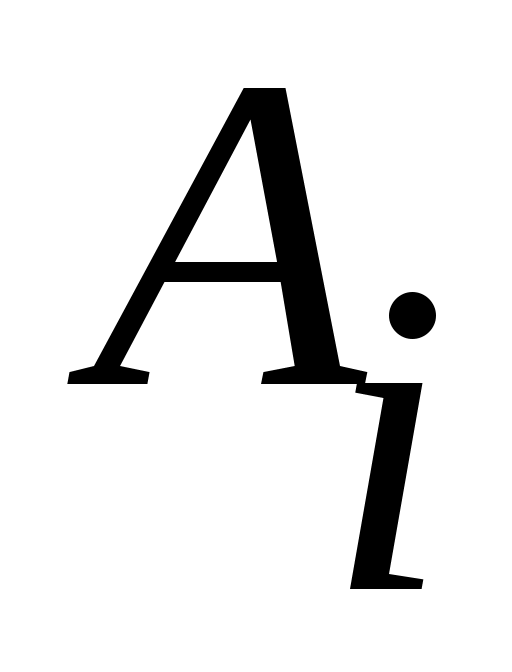 жиындарының саналымды бірігуі (қиылысуы)» деп айтамыз. жиындарының саналымды бірігуі (қиылысуы)» деп айтамыз.
Егер қайсыбір тұжырым 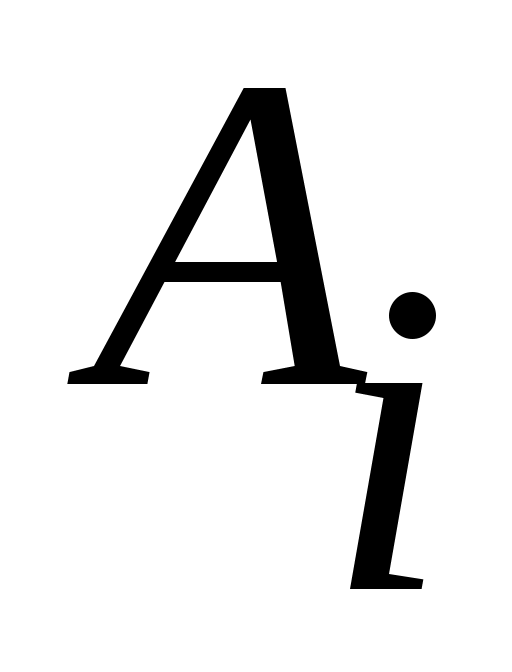 жиындарының ақырлы бірігуі (ақырлы қиылысуы) үшін де, саналымды бірігуі (саналымды қиылысуы) үшін де орындалатын болса, онда жиындарының ақырлы бірігуі (ақырлы қиылысуы) үшін де, саналымды бірігуі (саналымды қиылысуы) үшін де орындалатын болса, онда 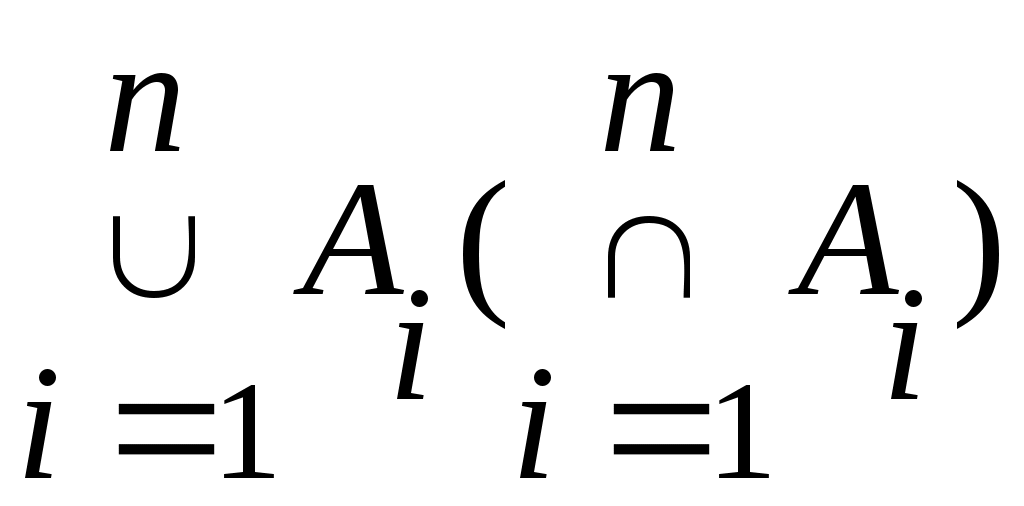 және және 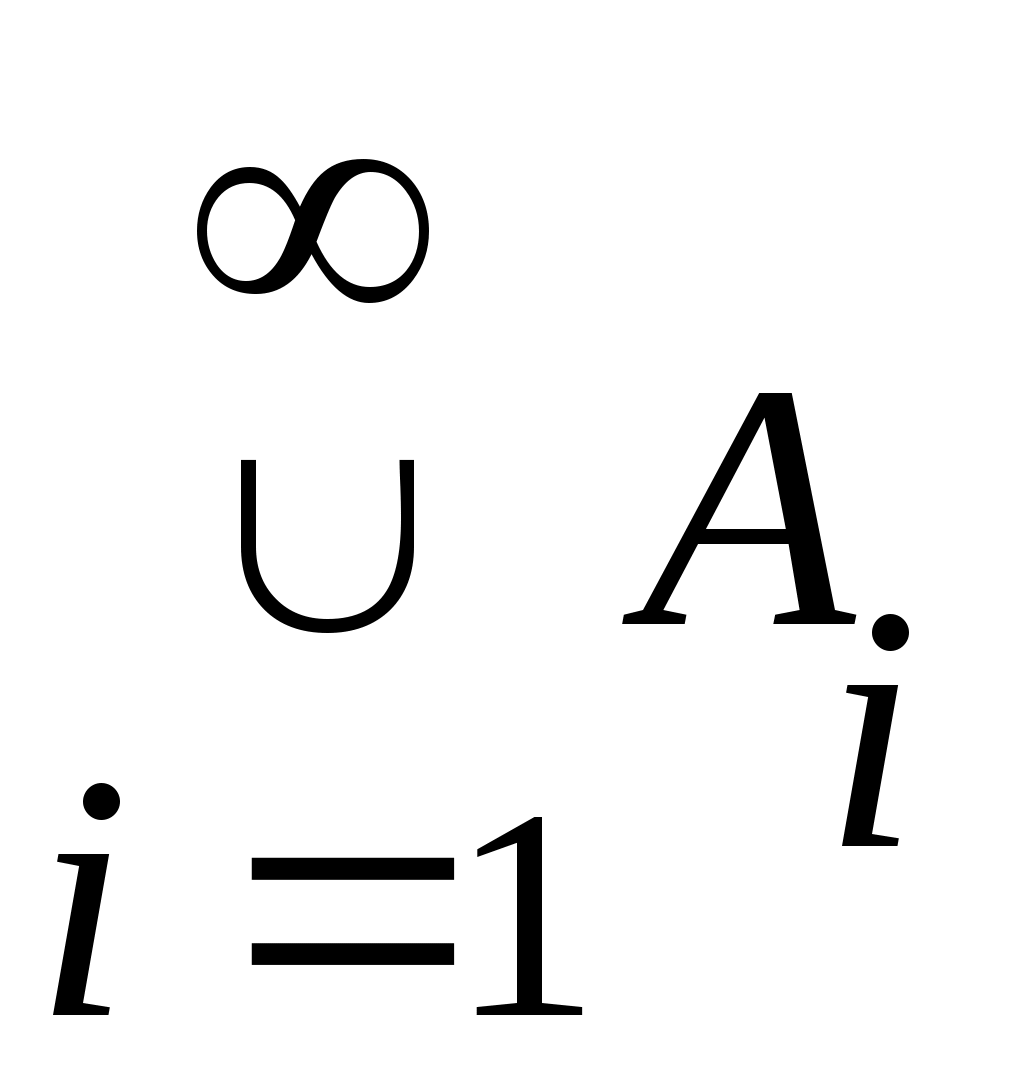 ( (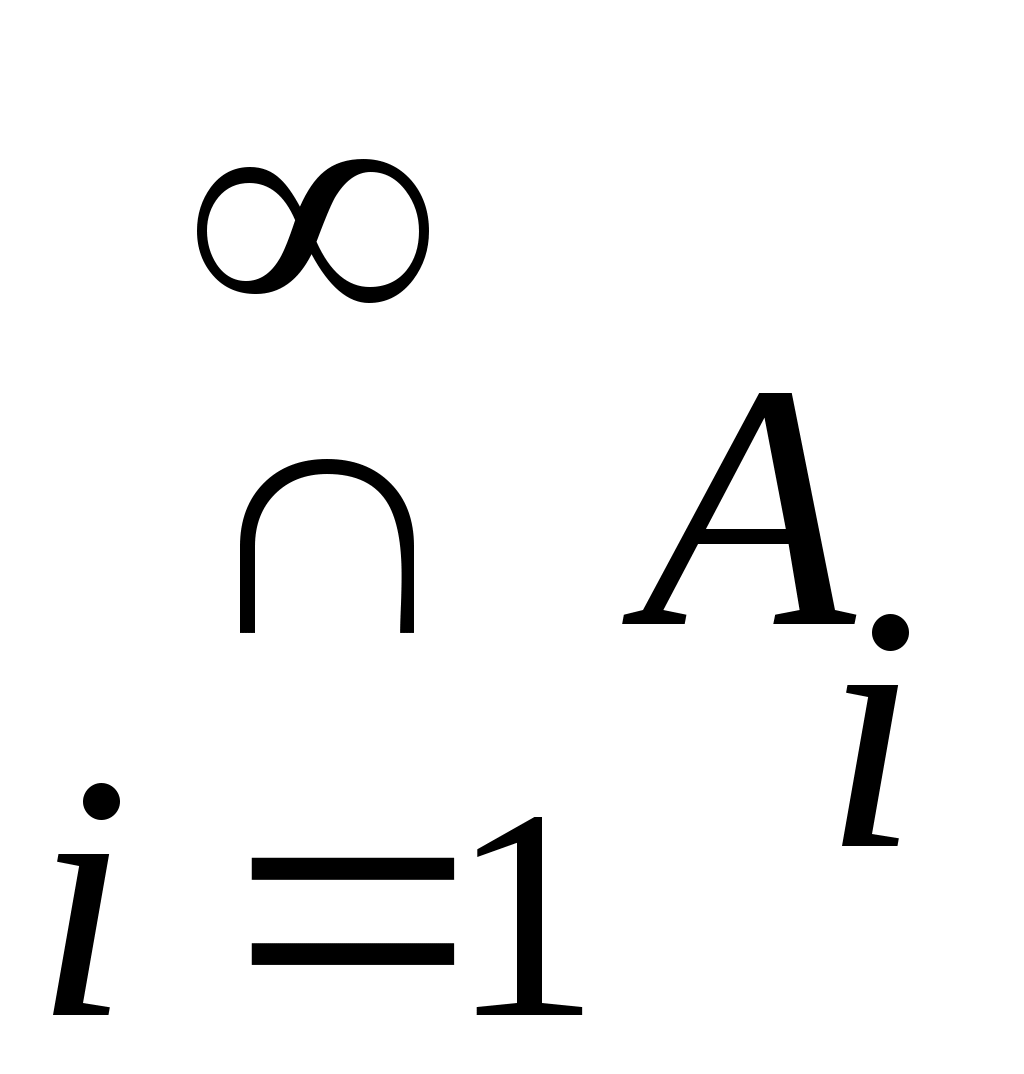 ) символдарының орнына ) символдарының орнына 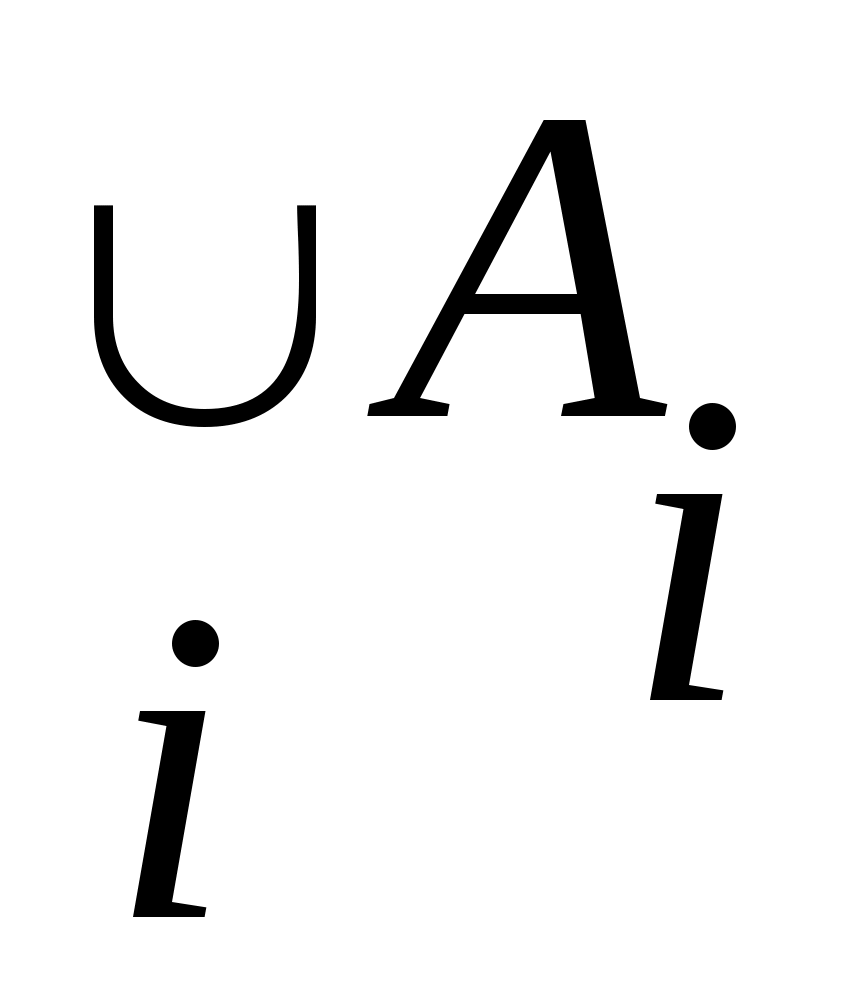 ( (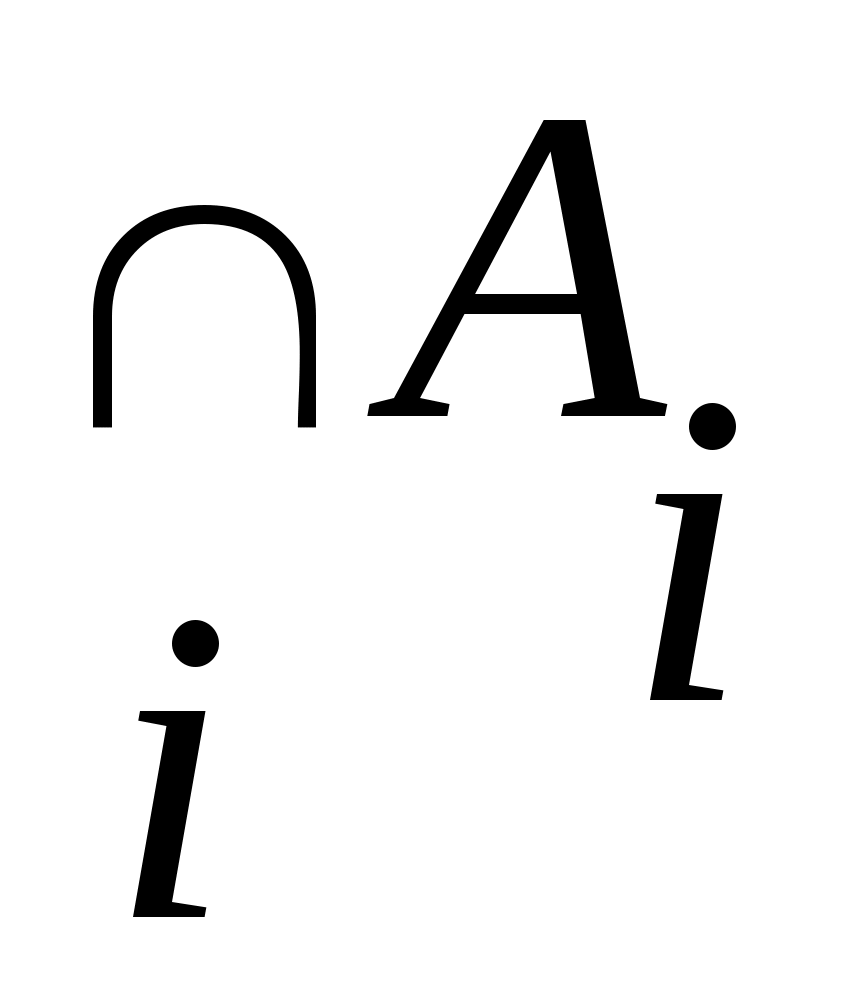 ) символын пайдаланамыз. Кейде ) символын пайдаланамыз. Кейде 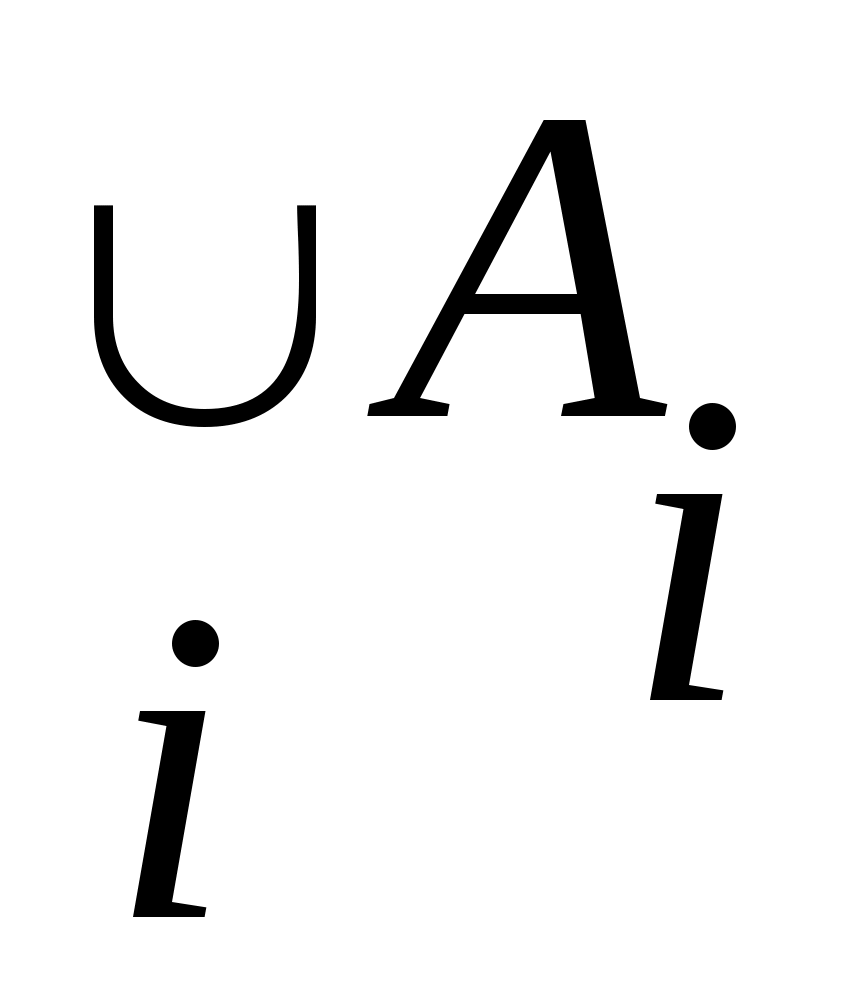 ( (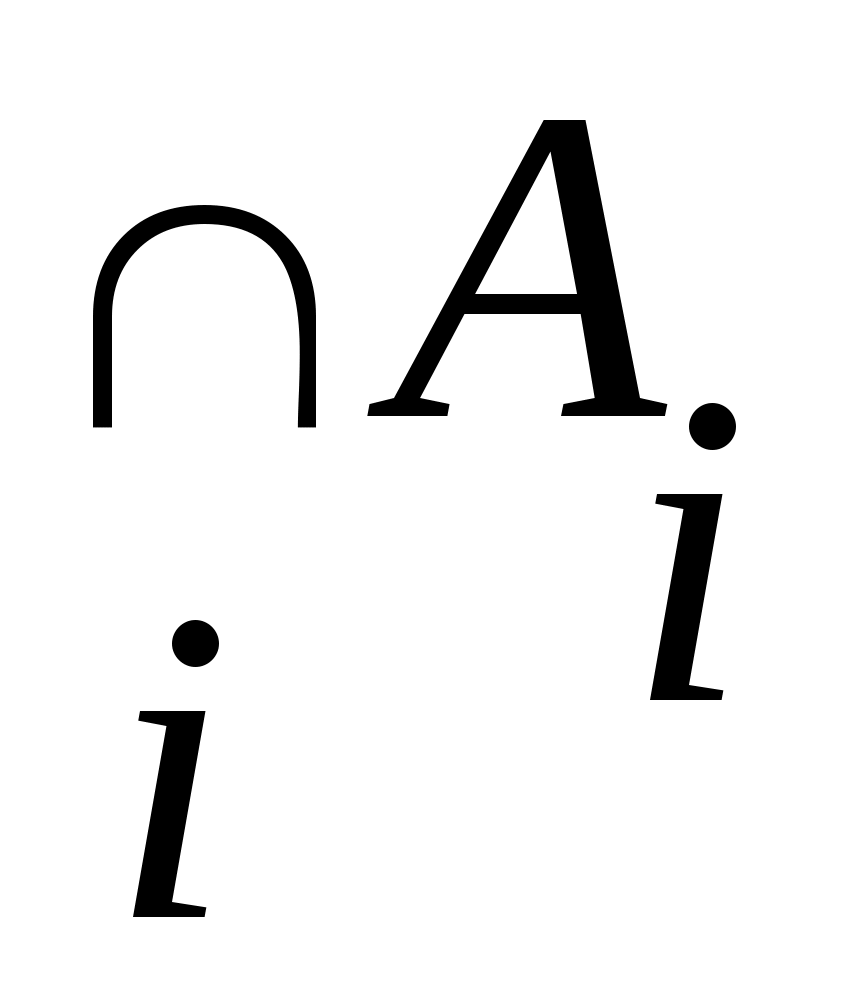 ) символы ) символы 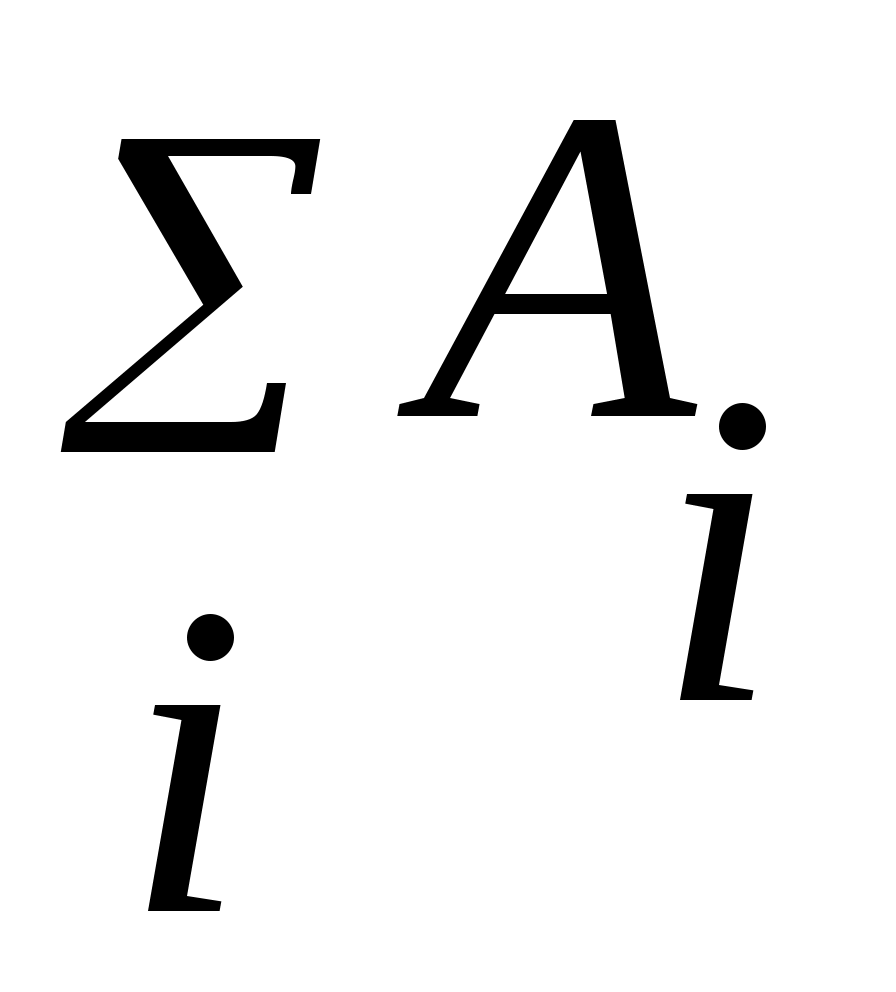 ( (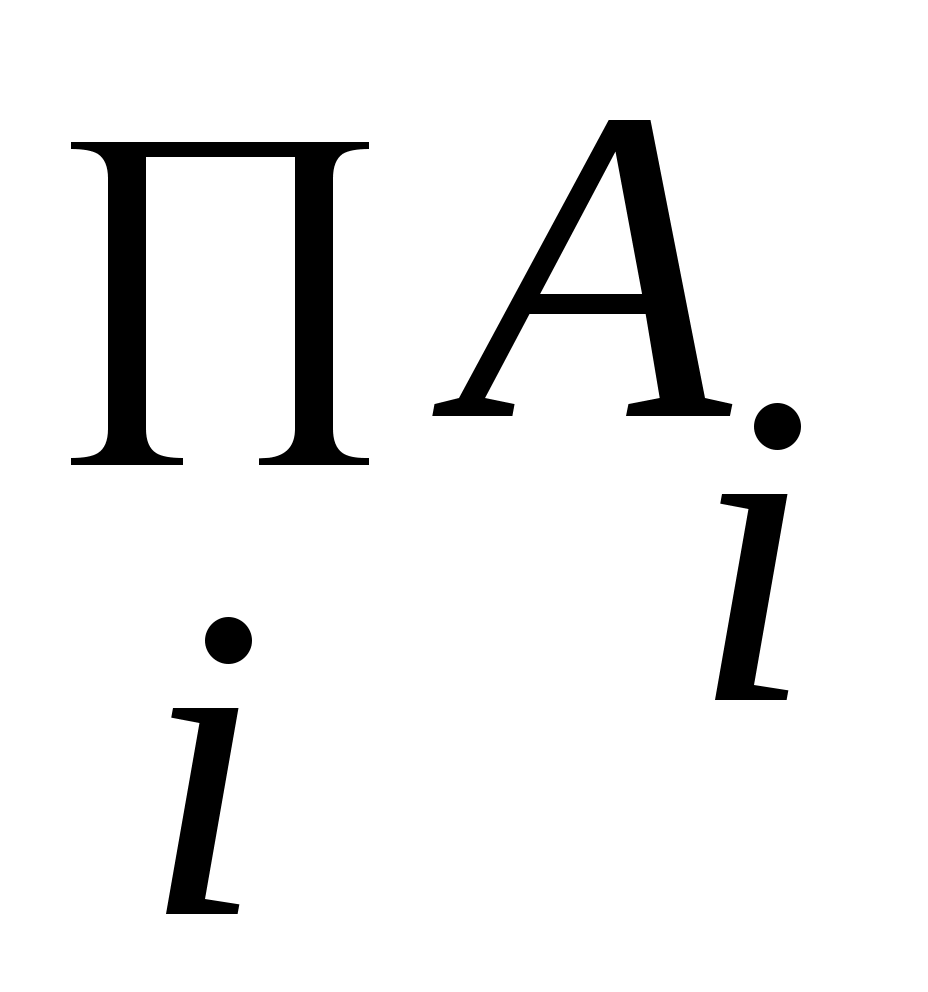 ) символына алмастырылып, « ) символына алмастырылып, «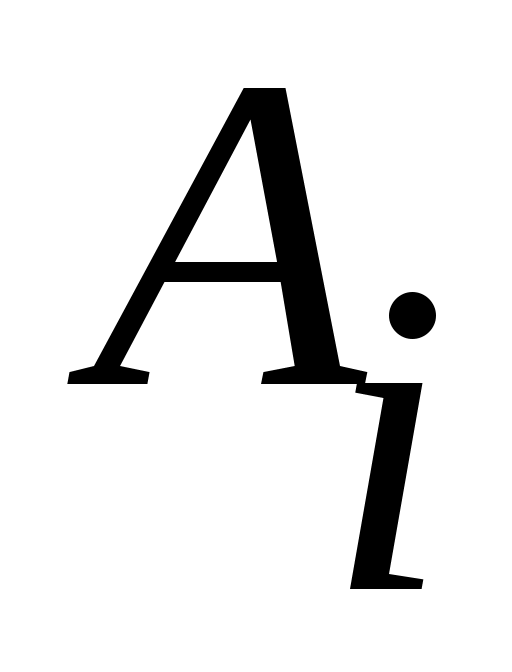 жиындарының қосындысы (көбейтіндісі)» деп те аталады. жиындарының қосындысы (көбейтіндісі)» деп те аталады.
2 – теорема. Егер 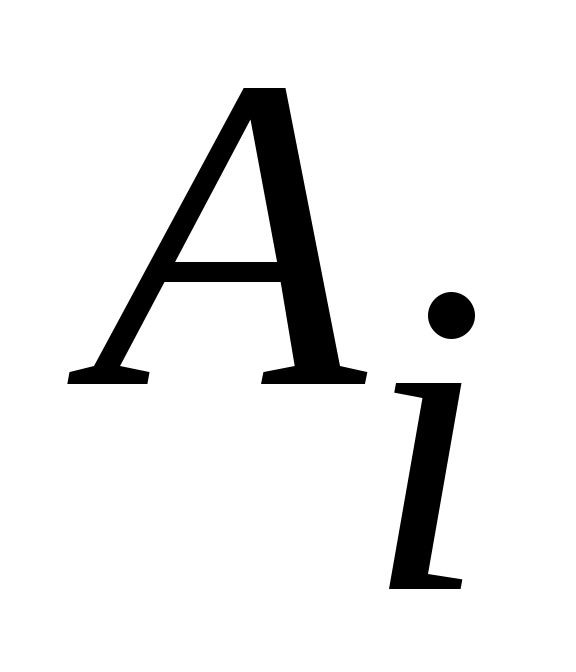 , ,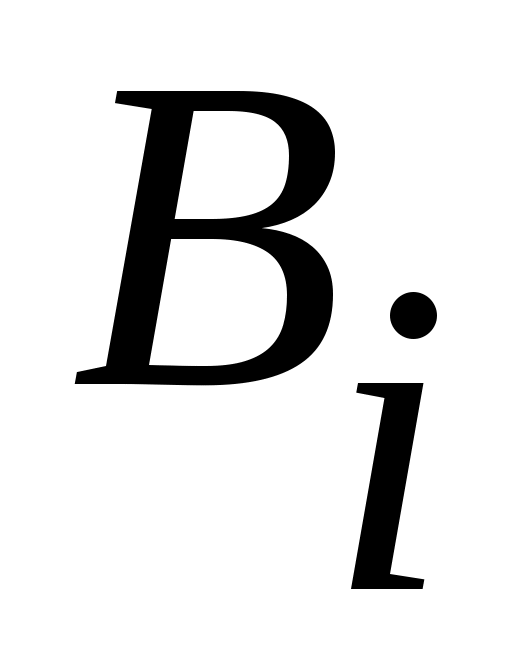 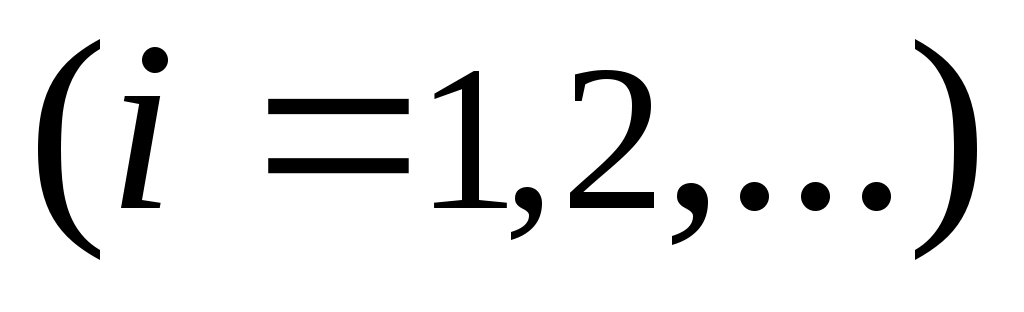 жиындары жиындары 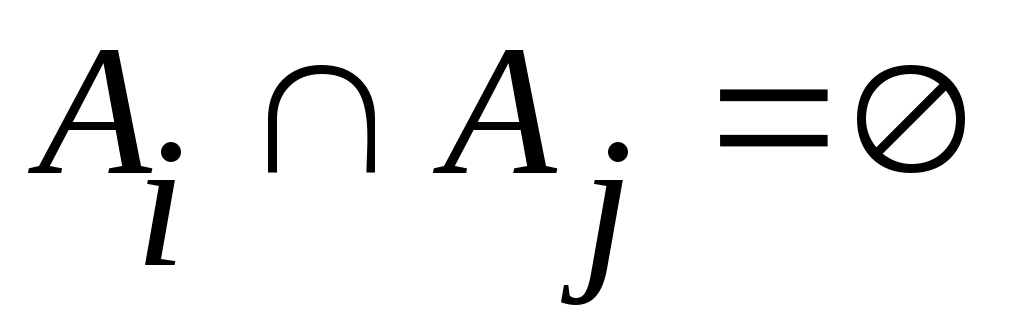 , , 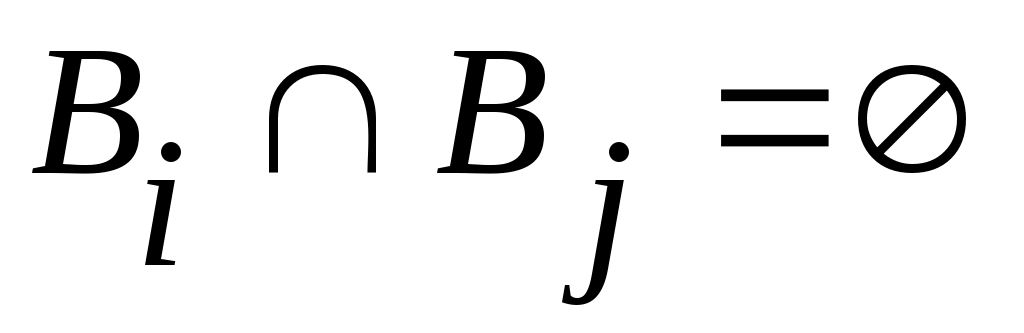
(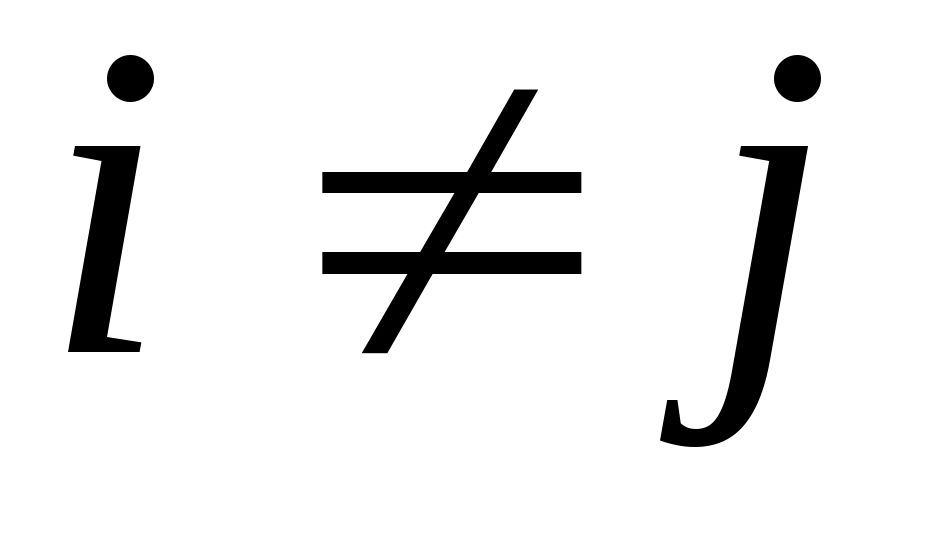 ) және ) және 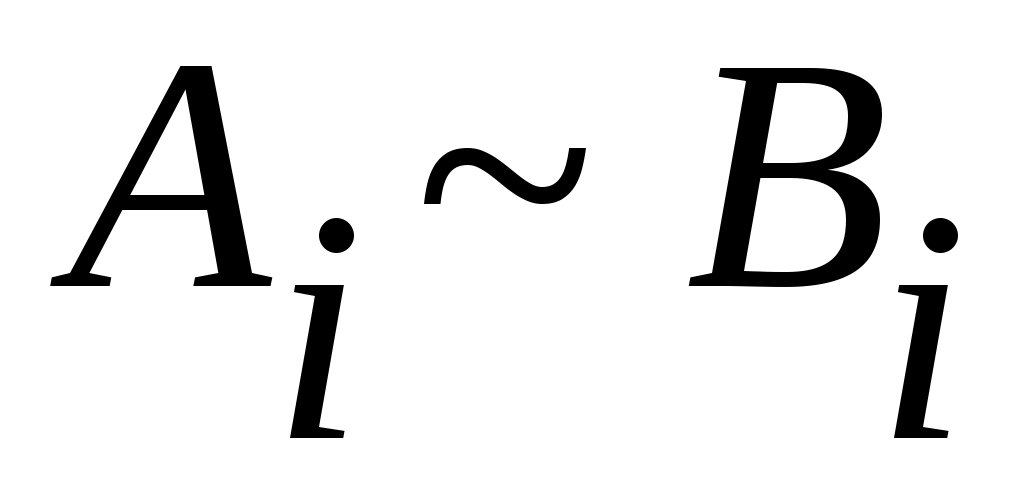 шарттарын қанағаттандыратын болса, онда шарттарын қанағаттандыратын болса, онда
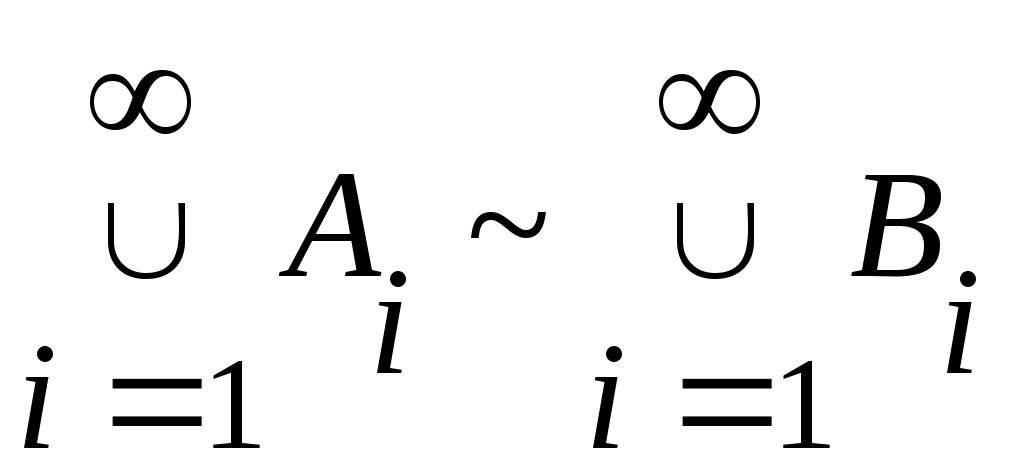 . .
Дәлелдеуі. 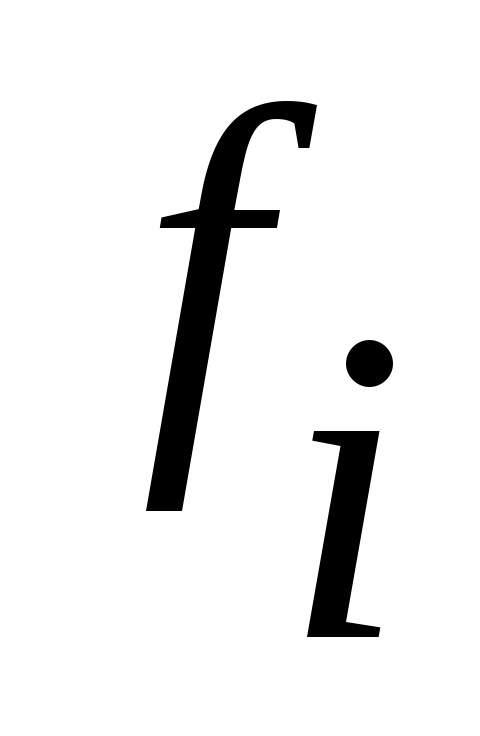 арқылы арқылы 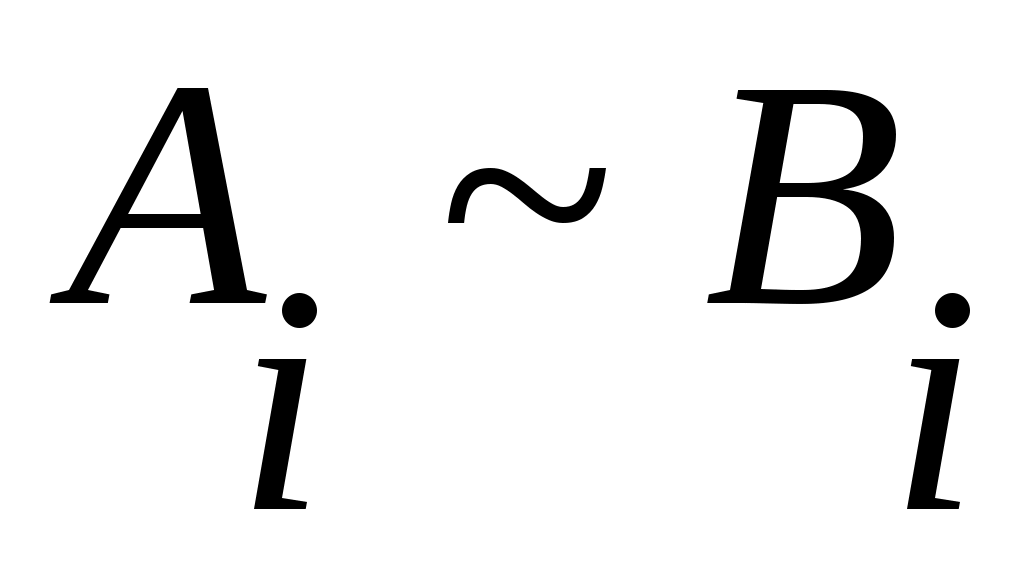 эквиваленттілігін беретін функцияны белгілейік. эквиваленттілігін беретін функцияны белгілейік. 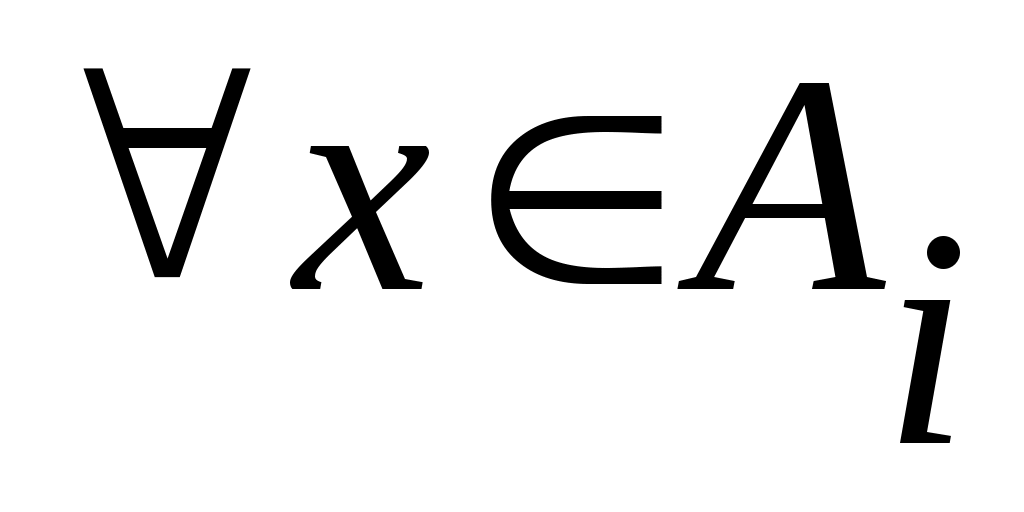 нүктесінде нүктесінде 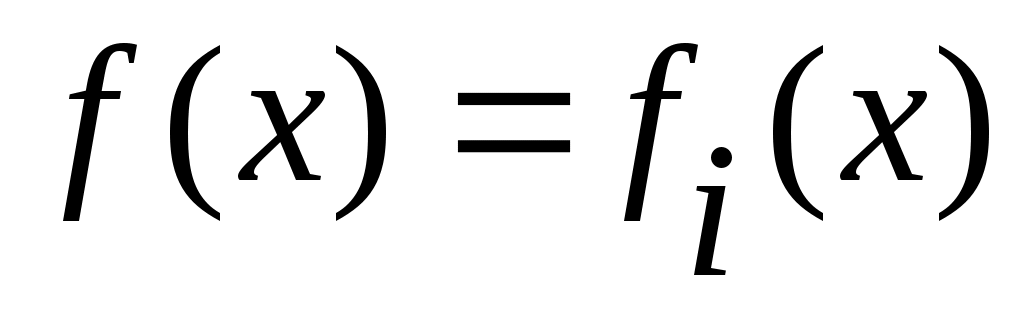 теңдігін қанағаттандыратын теңдігін қанағаттандыратын 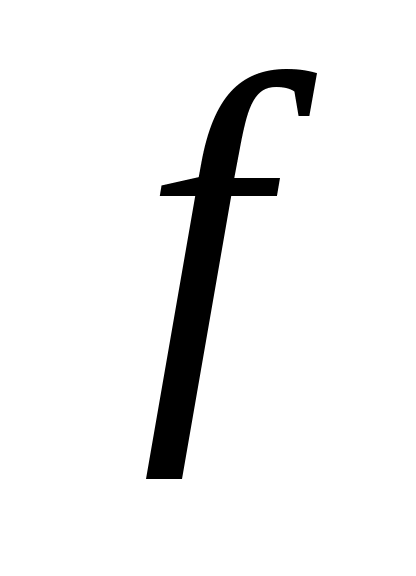 функциясы функциясы 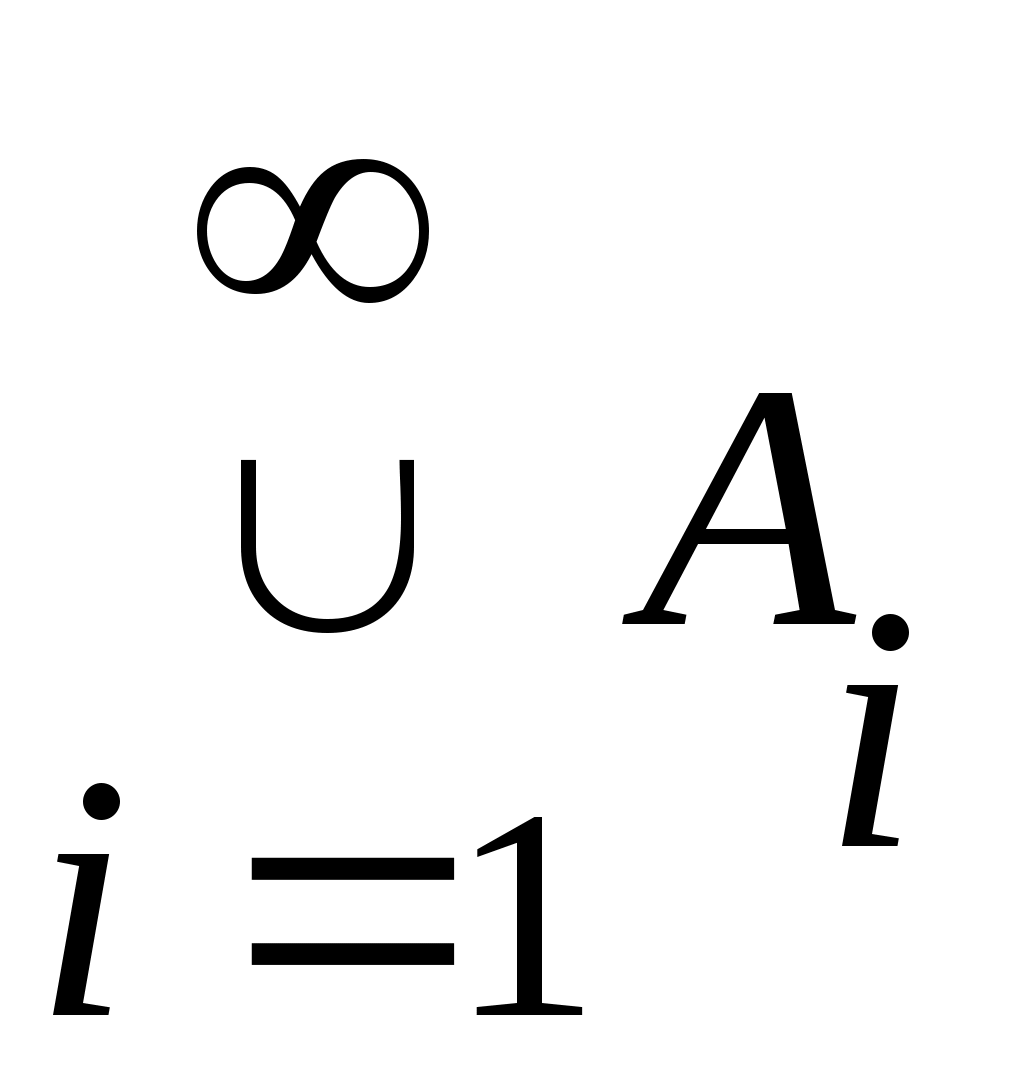 және және 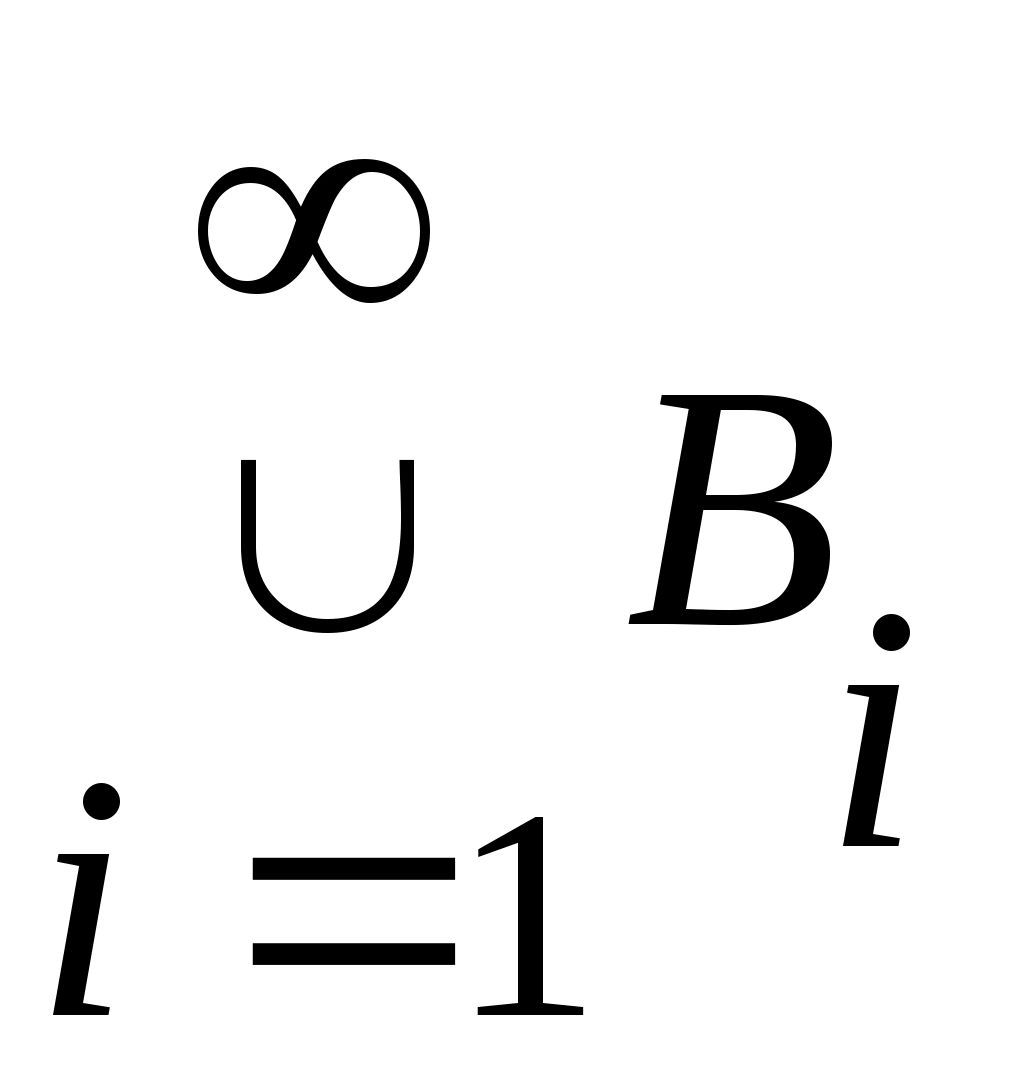 жиындары арасында өзара бірмәнді сәйкестік орнатады. жиындары арасында өзара бірмәнді сәйкестік орнатады.
3 – теорема. 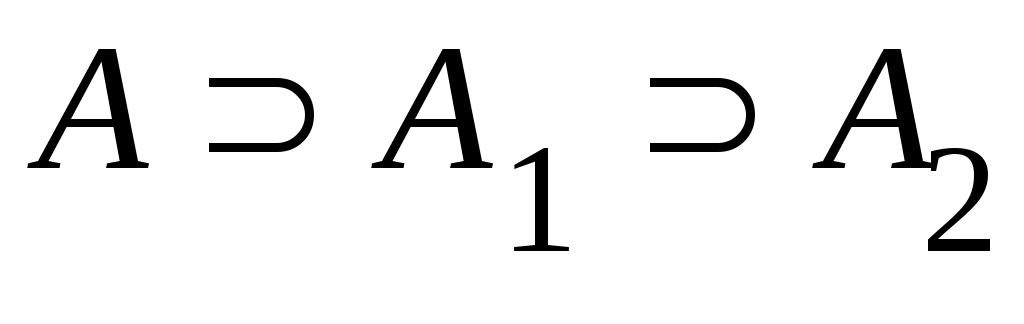 жиындары берілсін. Егер жиындары берілсін. Егер 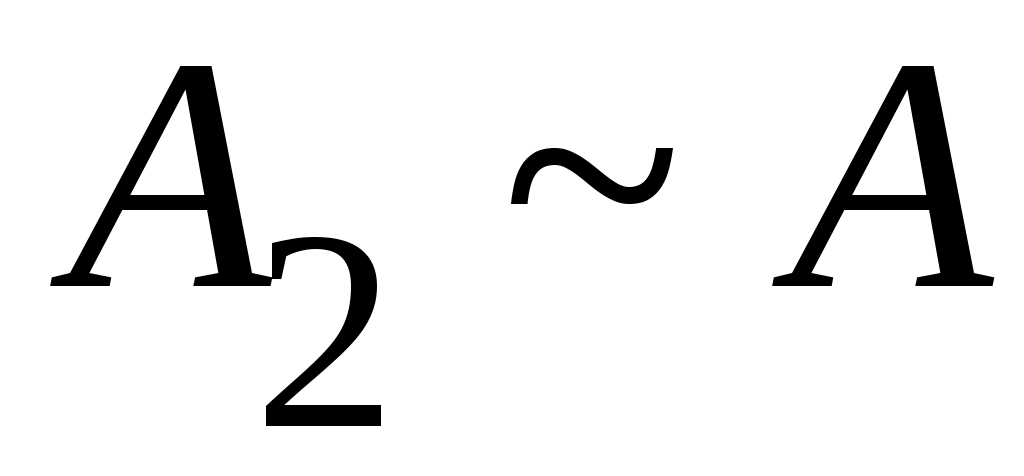 болса, онда болса, онда 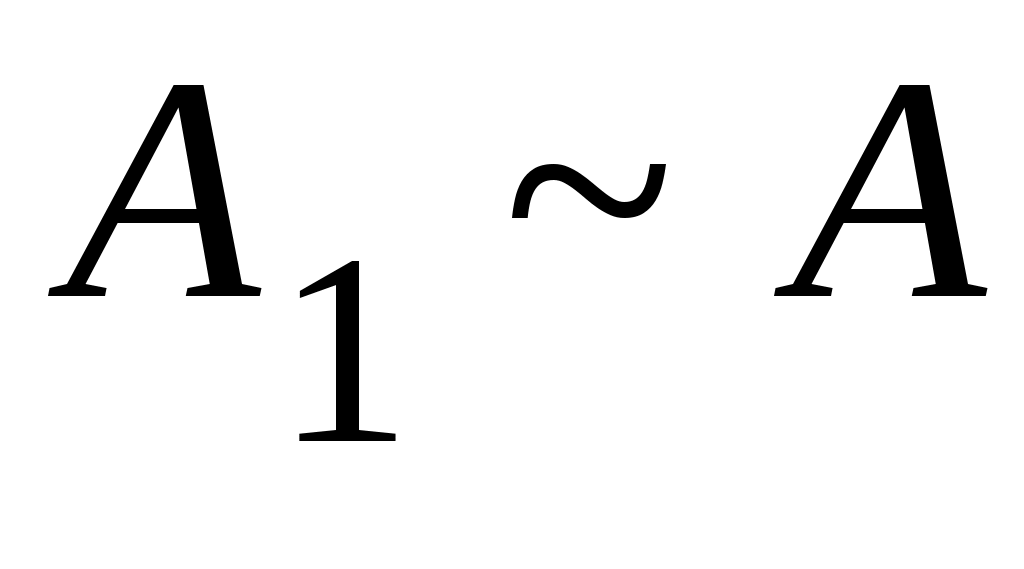 болады. болады.
Дәлелдеуі.  арқылы арқылы 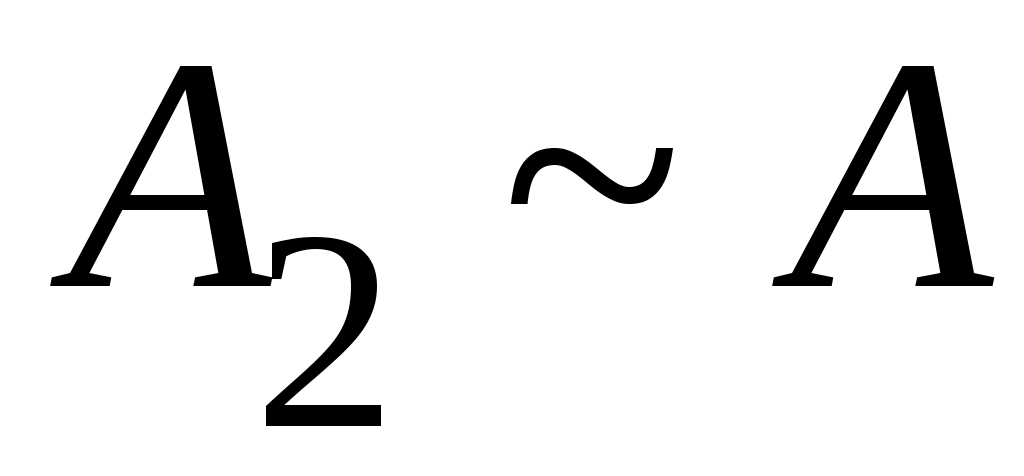 эквиваленттілігін беретін функцияны белгілейік. эквиваленттілігін беретін функцияны белгілейік. 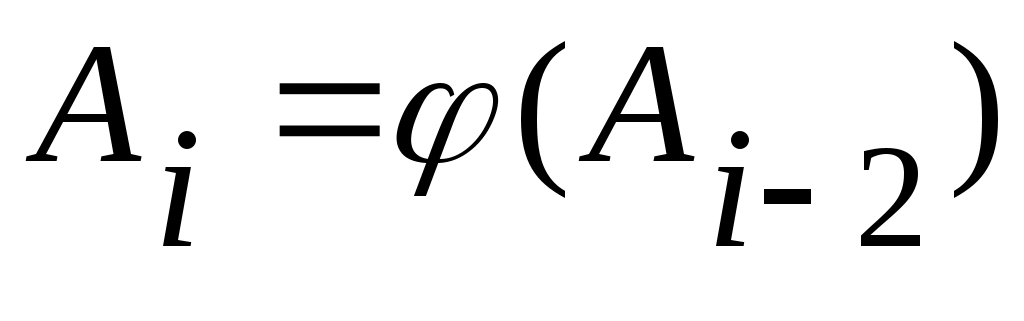 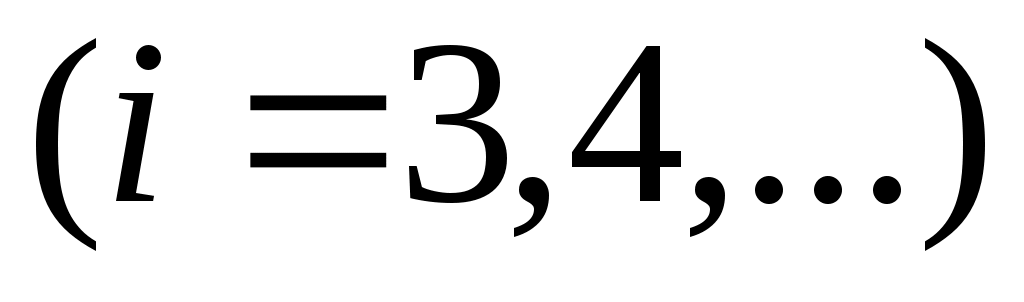 теңдігі бойынша анықталған теңдігі бойынша анықталған 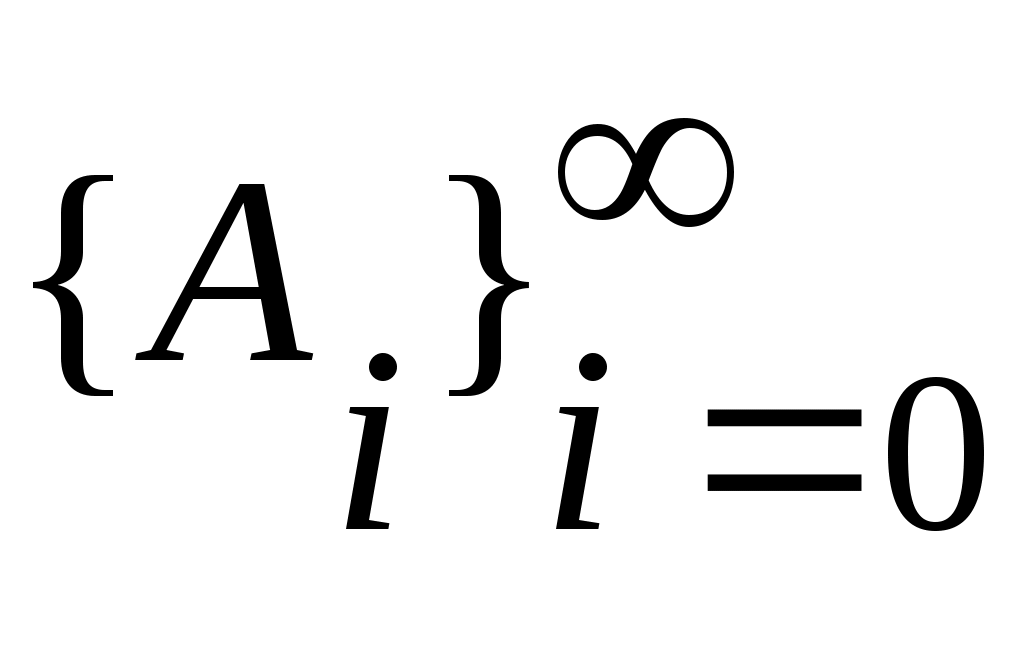 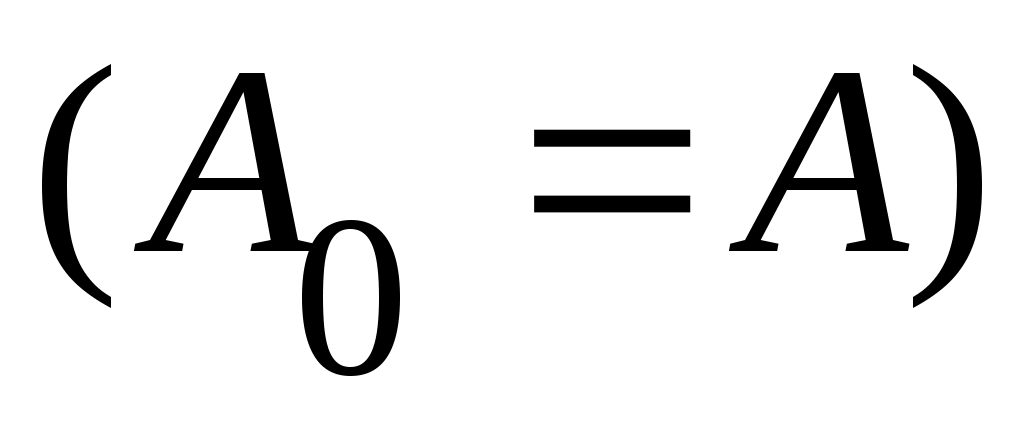 тізбегін қарастырайық. Әрбір тізбегін қарастырайық. Әрбір 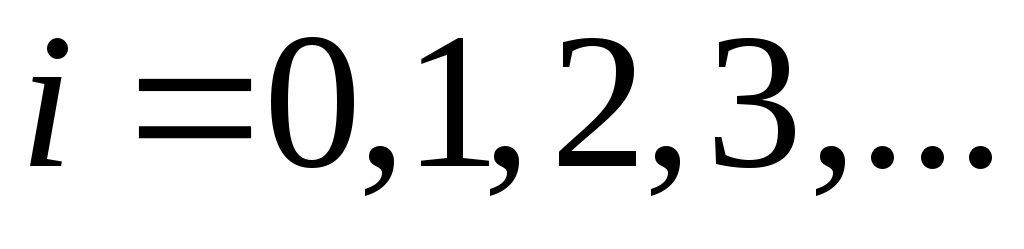 үшін үшін 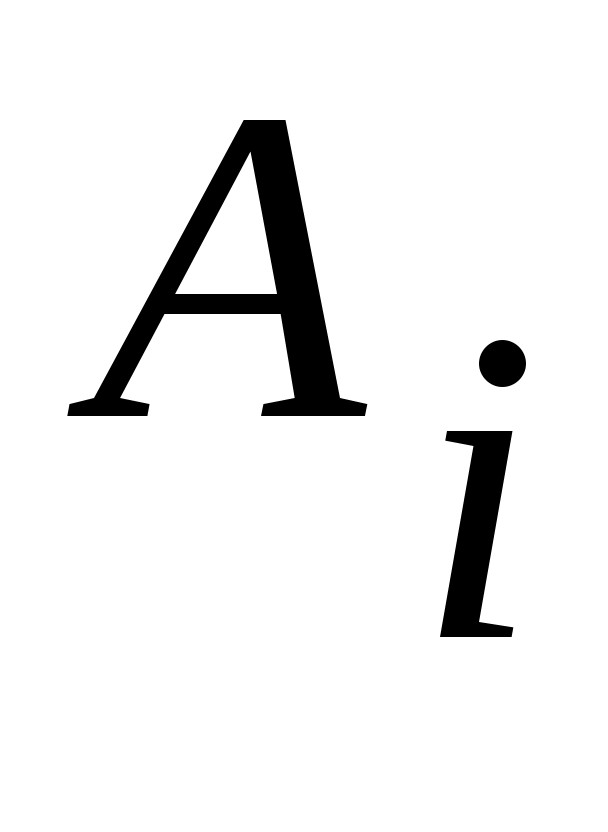 жиыны жиыны 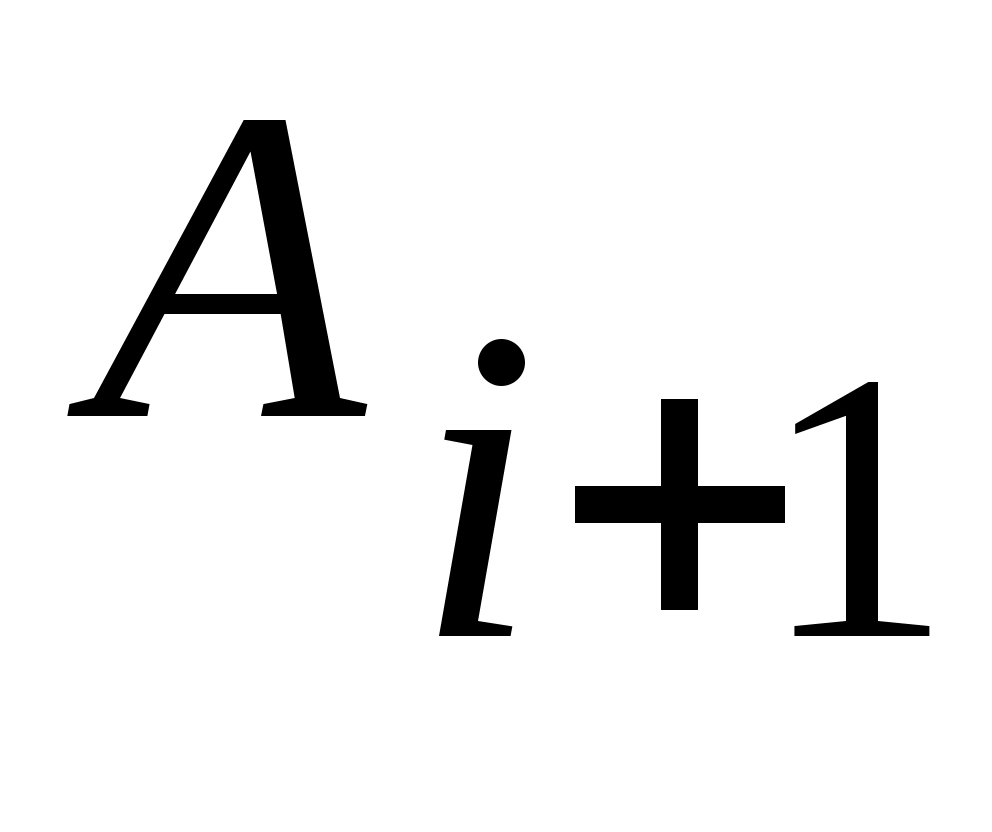 жиынын қамтитындықтан, жиынын қамтитындықтан,
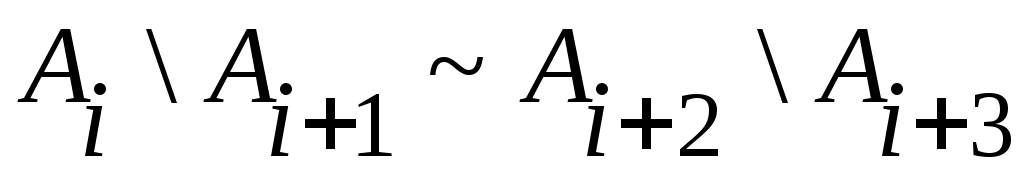 . (1) . (1)
эквиваленттілігі орындалады. 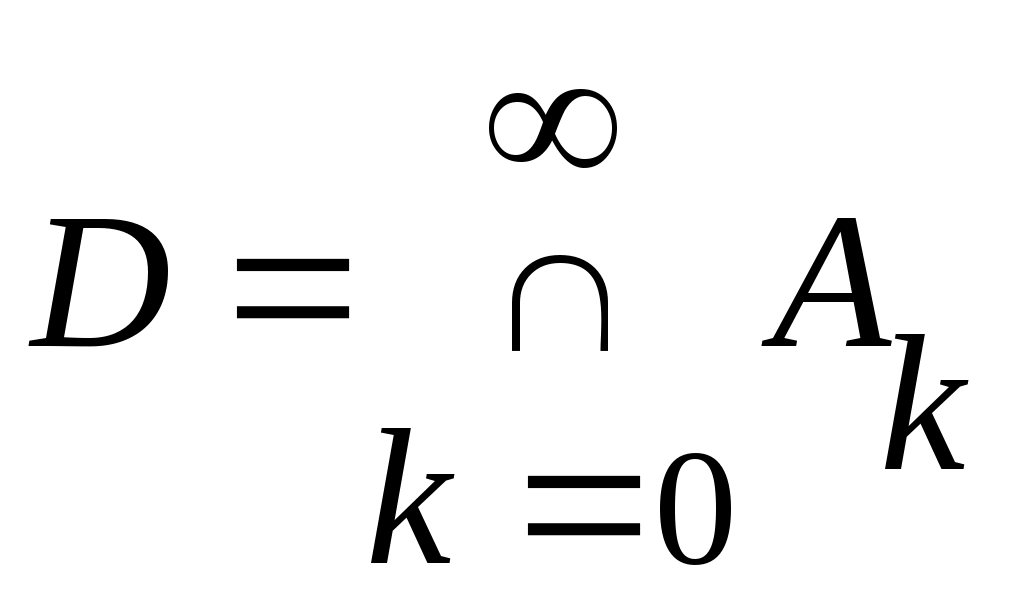 жиынын қарастырсақ, мына теңдіктерді жаза аламыз: жиынын қарастырсақ, мына теңдіктерді жаза аламыз:
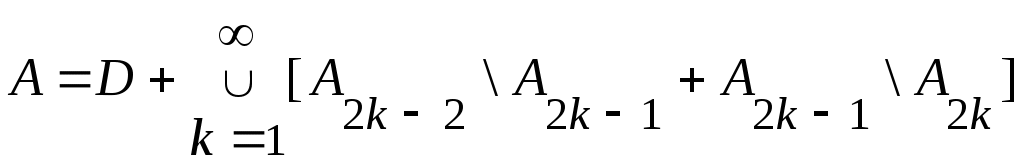 , ,
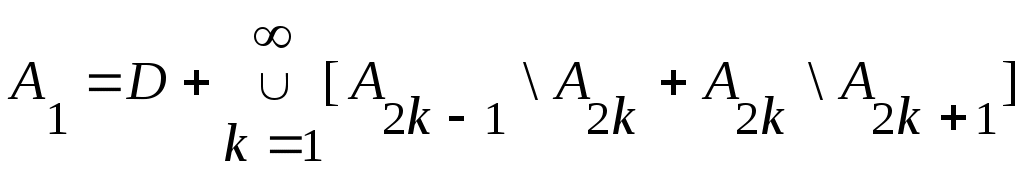 . .
(1) эквиваленттілігі бойынша
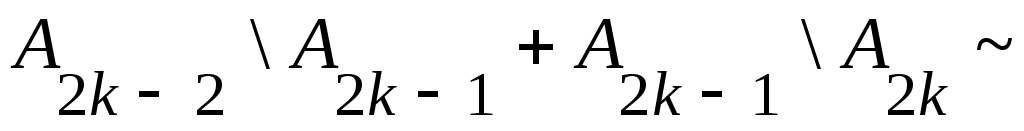 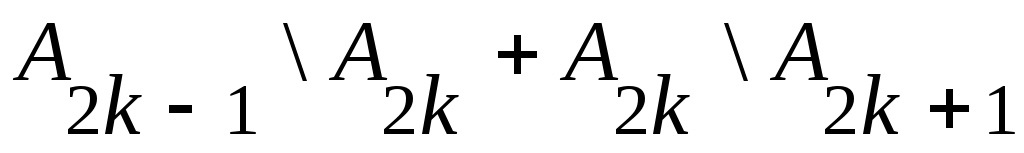 . .
Енді 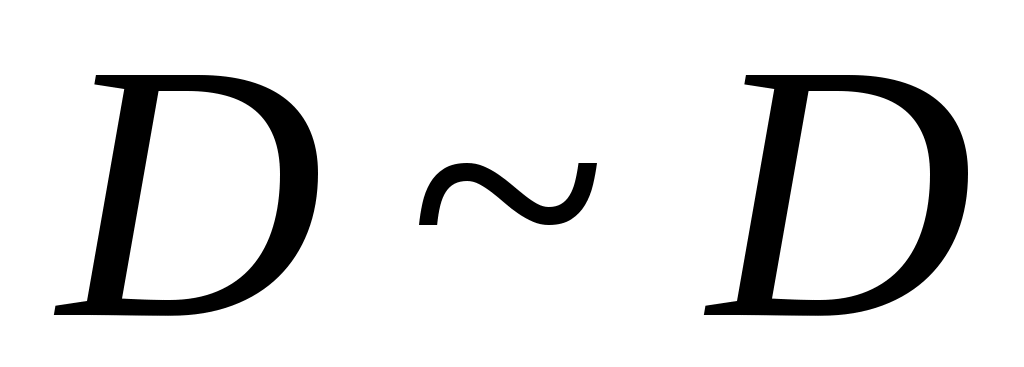 эквиваленттілігін ескеріп, 2 – теоремаға жүгінсек, эквиваленттілігін ескеріп, 2 – теоремаға жүгінсек, 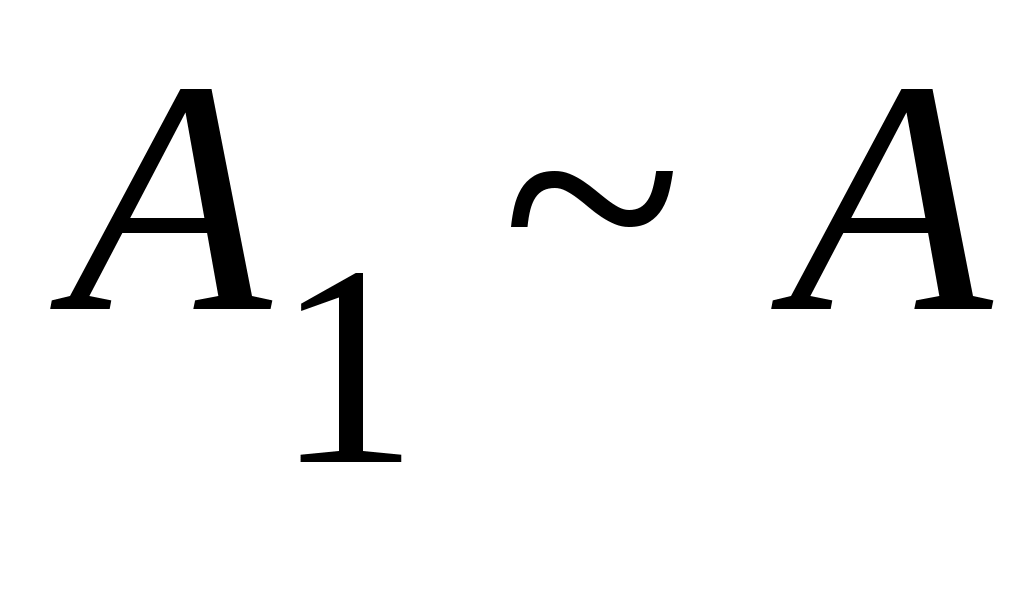
эквиваленттілігін аламыз.
Төмендегі 4 – теорема «Кантор – Бернштейн теоремасы» деген атауға ие (қараңыз, ([3], 34 – бет), ([4], 11– бет)).
4 – теорема. Егер 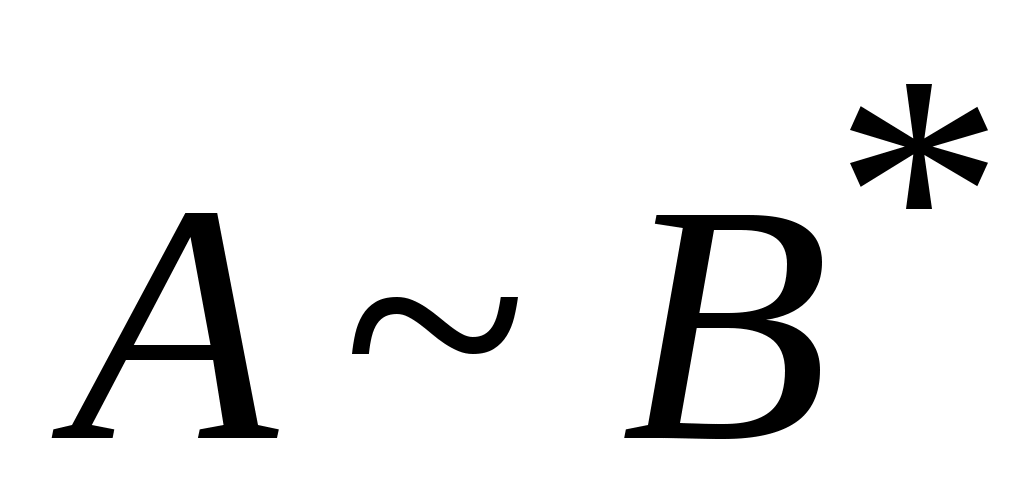 ( ( ) және ) және 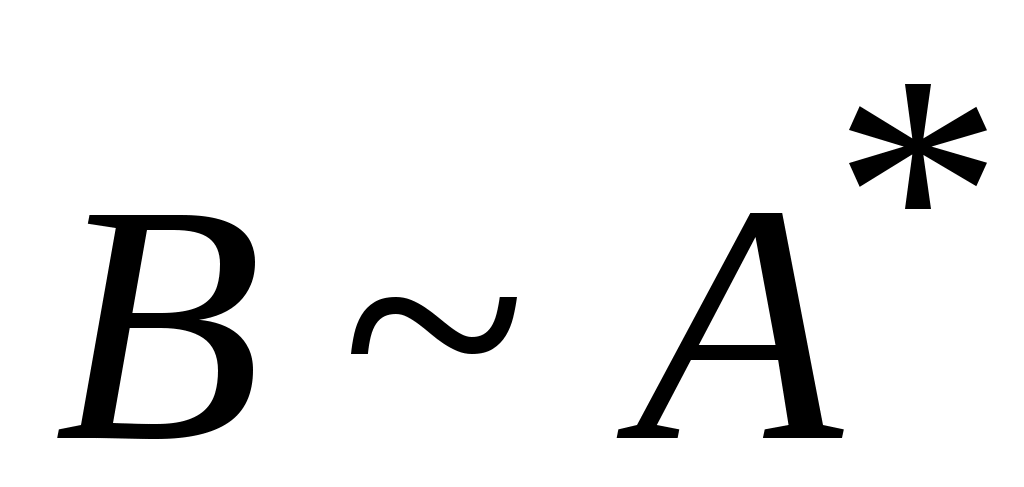 ( ( ) болса, онда ) болса, онда 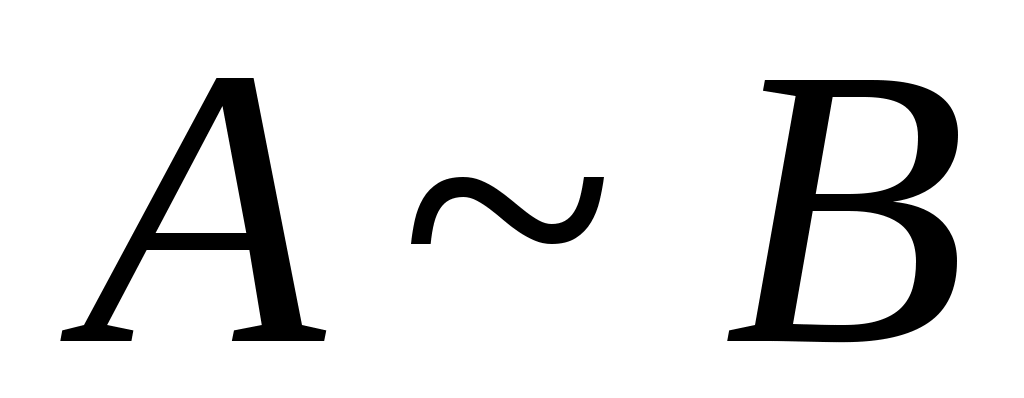 болады. болады.
Дәлелдеуі.  арқылы арқылы 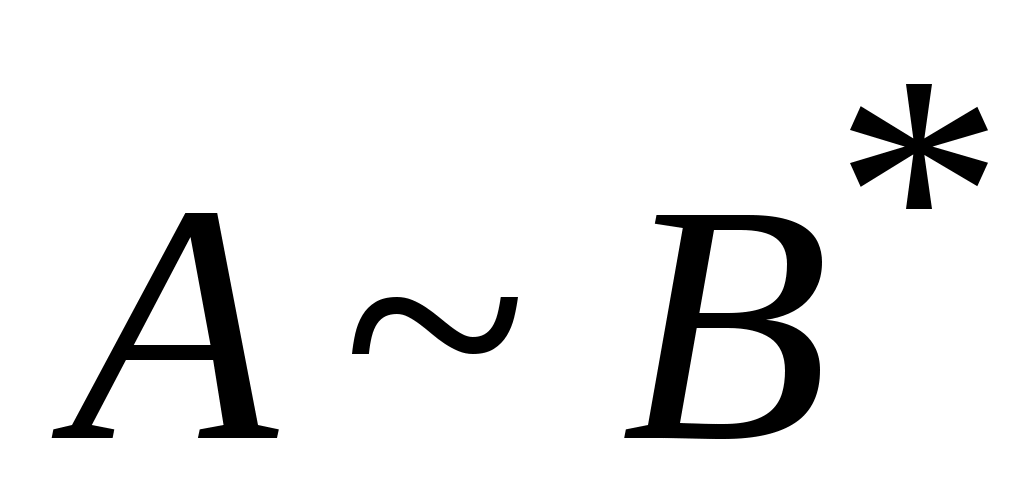 эквиваленттілігін беретін функцияны белгілейік. эквиваленттілігін беретін функцияны белгілейік. 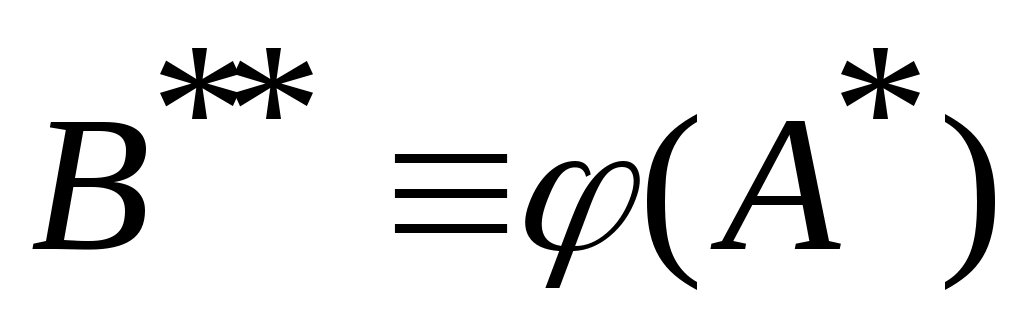 жиыны үшін жиыны үшін  , өйткені, , өйткені, 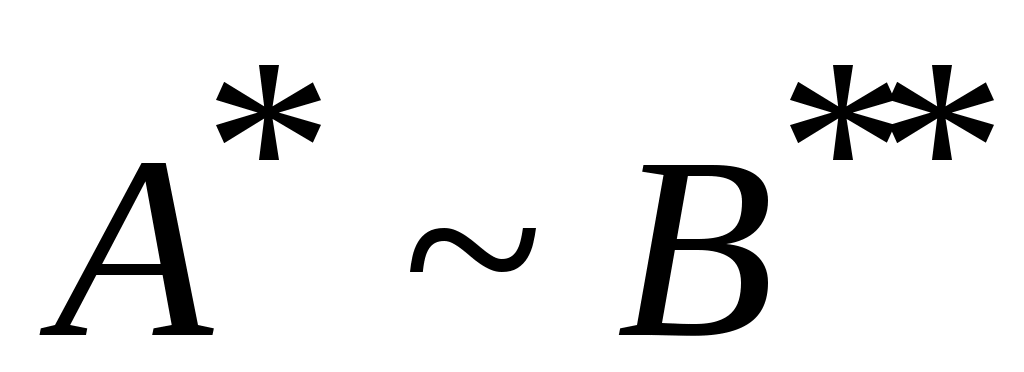 , ,  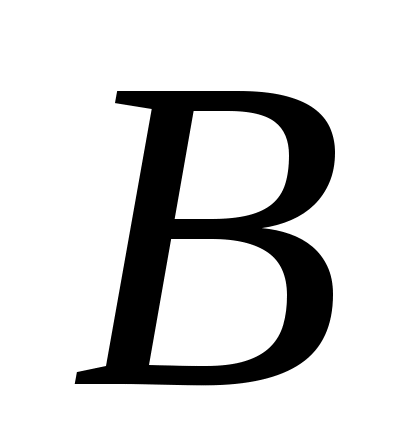 . Ал . Ал 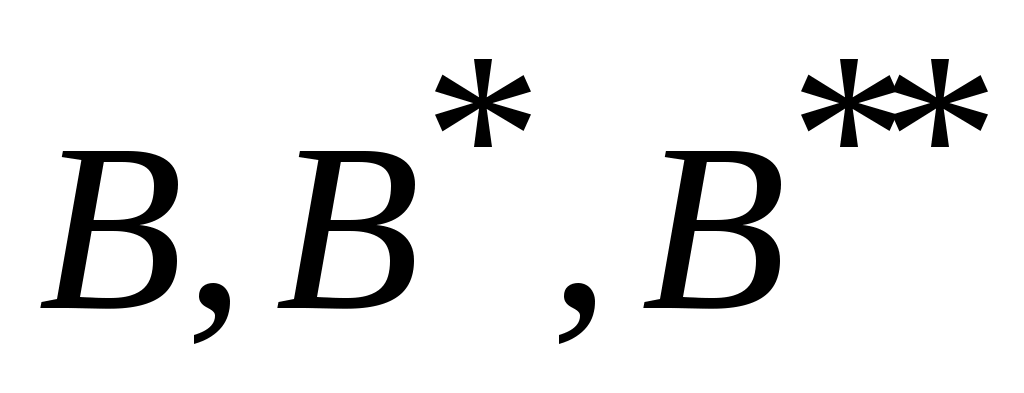 жиындары 3 – теорема шарттарын қанағаттандырады. Ендеше, жиындары 3 – теорема шарттарын қанағаттандырады. Ендеше, 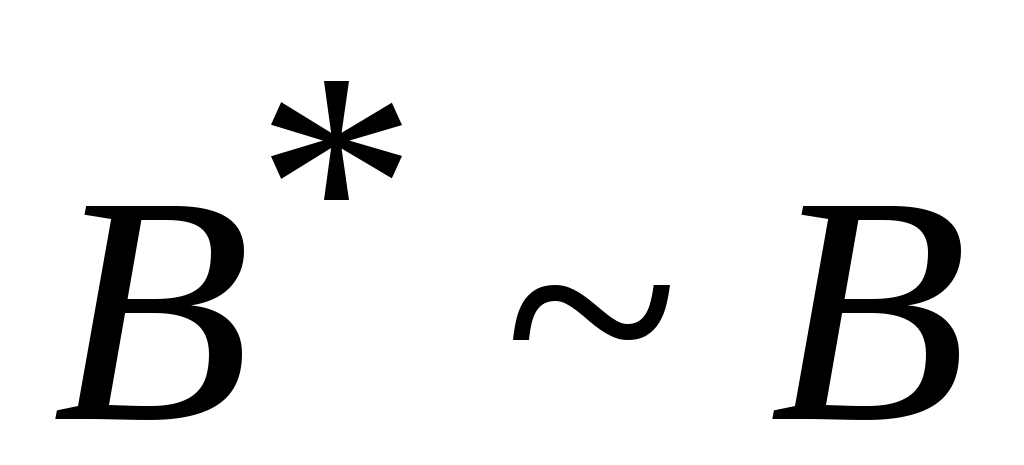 . Енді . Енді 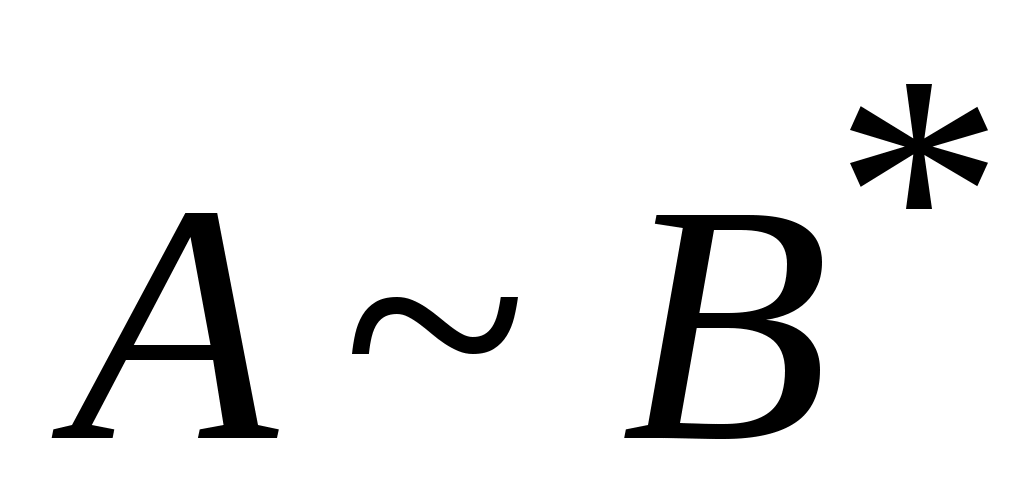 эквиваленттілігін ескерсек, эквиваленттілігін ескерсек, 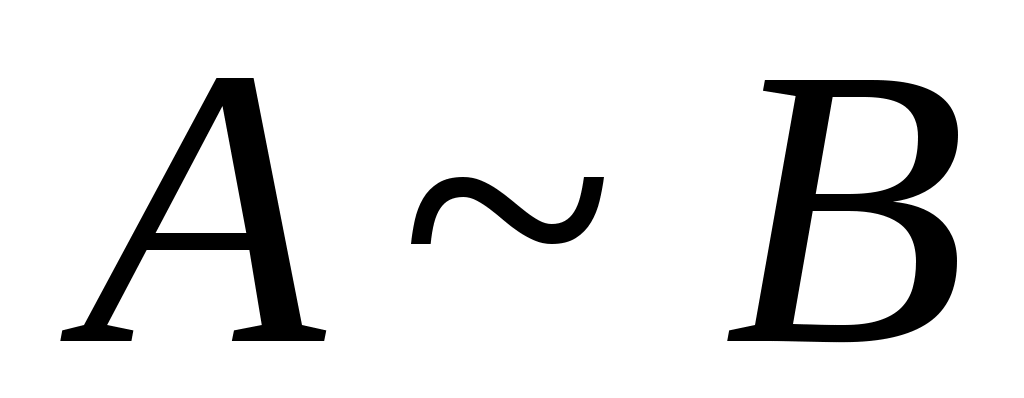 . .
|
|
|
 Скачать 1.5 Mb.
Скачать 1.5 Mb.