3. 2 Д_рістер материалдарын о_у_а методикалы_ жетекшілік 1-Та_ыр. 3. 2 Дрістер материалдарын оуа методикалы жетекшілік 1Таырып. Метрикалы кеістіктер

• Название: 3. 2 Дрістер материалдарын оуа методикалы жетекшілік 1Таырып. Метрикалы кеістіктер
• Дата: 08.12.2020
• Размер: 494 Kb.
• Имя файла: 3. 2 Д_рістер материалдарын о_у_а методикалы_ жетекшілік 1-Та_ыр.doc
• Тип: Документы; #158512
• страница: 1 из 3

Дәрістерді оқуға Форма

әдістемелік жетекшілік ФМО ПГУ 7 18 207

математика кафедрасы

3.2 Дәрістер материалдарын оқуға методикалық жетекшілік
1-Тақырып. Метрикалық кеңістіктер.

1-дәріс. Дәріс мазмұны. Метрикалық кеңістіктің анықтамасы, мысалдары. Метрикалық кеңістік кез келген Х жиынында құрылады.

Анықтама 1. Х жиынының кез келген х және у элементтерінде, төмендегі аксиомаларды қанағаттандыратын теріс емес саны:

1. (тепе-теңдік аксиомасы);

2. (симметрия аксиомасы);

3. Х жиынының кез келген x, y, zэлементтерінде теңсіздігі орындалады (үшбұрыш аксиомасы),

осы элементтердің арасындағы қашықтық деп аталады.

Анықтама 2. Элементтерінің арасындағы қашықтық анықталған Х жиыны метрикалық кеңістік деп аталады.

Сонымен, метрикалық кеңістік – жиын мен осы жиында анықталған қашықтықтан тұратын қосақ: .

Метрикалық кеңістіктердің жиі кездесетін мысалдары:

және басқалар (1. 57-65 беттер).

Метрикалық кеңістіктерде үшбұрыш аксиомасының орындалатынын тексергенде жиі қолданылатын теңсіздіктер:

1. Коши-Буняковский теңсіздігі: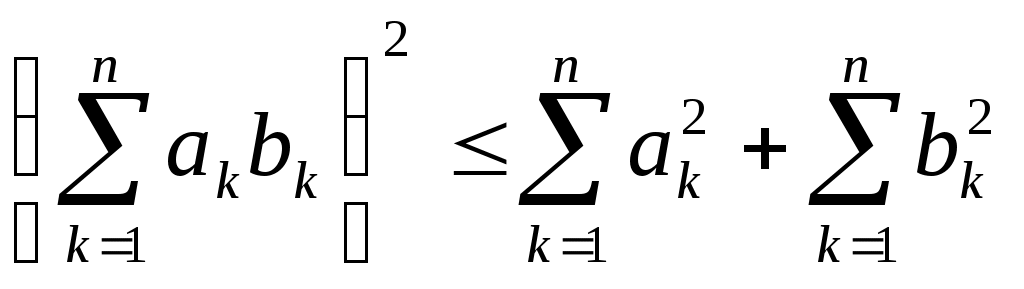

.

және оның салдары: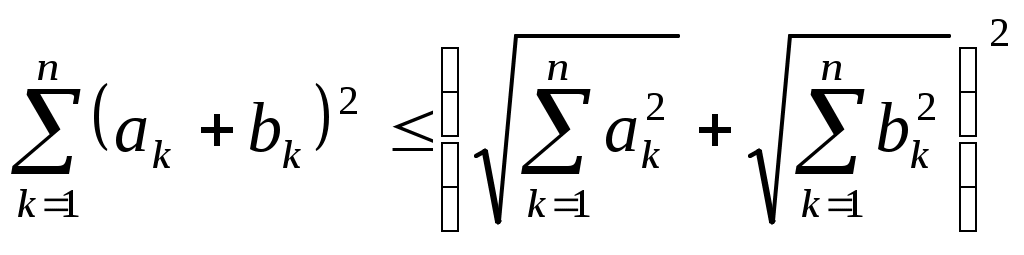

.

2. Гельдер теңсіздігі: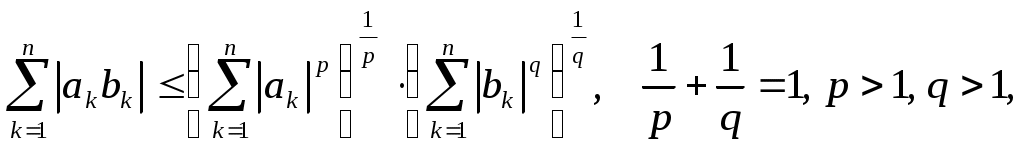



3. Минковский теңсіздігі: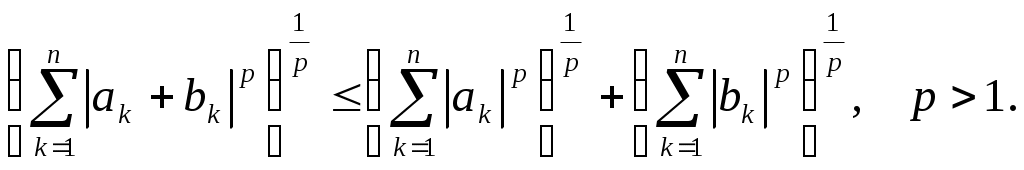



Осы теңсіздіктердің дәлелдеуін білу керек (1, 62-65 беттер).
2-дәріс. Метрикалық кеңістіктеріндегі топологикалық ұғымдар. Метрикалық кеңістіктердегі топологикалық ұғымдарға шар және шар арқылы анықталатын нүктенің маңайы жатады. Ашық, тұйық жиындар және жиынның тұйықтамы туралы ұғымдар. Осы жиындардың қасиеттері мен олардың арасындағы байланыстар туралы теоремалар.

Метрикалық кеңістіктердің негізгі типтері:

* толық метрикалық кеңістік,

* сепарабельді метрикалық кеңістік.

Осы тақырып бойынша студенттер білуі керек:

- метрикалық кеңістік және осындай кеңістіктегі тополгиялық ұғымдарды (шар, нүктенің маңайы, олардың жиі қолданылатын метрикалық кеңістіктердегі мысалдары)

- жиынның ішкі, сыртқы, шектік, оңаша нүктеледің анықтамаларын.

- метрикалық кеңістіктегі ашық, тұйық жиындарды, мысалдарын;

- жиынның тұйықтамын;

- метрикалық кеңістіктегі ашық және тұйық жиындар туралы теоремаларды;

- берілген жиында тығыз және барлық жерде тығыз жиындар туралы ұғым;

- толық және және сепарабельді кеңістіктер және олардың мысалдары.

Екінші тақырыпқа 2 дәріс және 4 жаттығу сабағы жоспарланған

3-дәріс. Толық метрикалық кеңістіктер туралы теоремалар.

Анықтама 1. R=(X, ) кеңістігіндегі нүктелер тізбегі берілсін. Егер кез келген оң саны бойынша санын, теңсіздігін қанағаттандыратын барлық n мен m нөмірлі нүктелері теңсіздігін қанағаттандыратындай етіп табуға болса, ода берілген тізбек фундаменталды деп аталады.

Определение 2. Барлық фундаменталды тізбектері өз ішінде жинақталатын R=(X, ) метрикалық кеңістігі толық деп аталады.

Теорема 1. Толық метрикалық кеңістіктегі радиусы нөлге ұмтылатын, бірінің ішінде бірі орналасқан тұйық шарлар тізбегінің қиылысуы бос жиын болмайды.

Бұл теорема бірінің ішінде бірі орналасқан сегменттер туралы лемманың кез келген тұйық кеңістіктегі жалпылануы болып табылады.

Қысылған бейнелер принципі.

Анықтама 3. R=(X, ) метрикалық кеңістігінің өзіне өзі А бейнеленуі осы кеңістіктің барлық нүктелері үшін



теңсіздігін қанағаттандыратын саны табылса, бұл бейнелеу қысылу деп аталады.

Теорема (Қысылған бейнелер принципі). Толық R метрикалық кеңістікте анықталған кез келген қысылу бейтеленуінің тек қана бір қозғалмайтын нүктесі болады.

Бұл принципті, әдетте, польша математигінің атымен Банах теоремасы деп атайды.

(1, стр., 67-97 беттер).

кеңістіктері толық метрикалық кеңістіктің мысалдары болып табылады. Рационал сандар кеңістігі Q және кеңістіктері толық болмайтын метрикалық кеңістіктердің мысалдарына жатады.

Толық емес метрикалық кеңістіктің толықтамасы. Толық емес Q кеңістігін толық кеңістігіне дейін толықтау процесін игеру. Осы процессті толық емес кез келген кеңістіктің толықтамасын құруға пайдалануға болатынын көрсету. Осы әдісті кеңістігінің толықтамасын құруға пайдалану. Толықтаманың нүтесі ретінде толвқталатын кеңістіктің фундаменталды тізбегі алыналатынына көңіл аударылуы керек. Бұл факт осы әдістің шешуші элементі екеніне назар аудару керек.

Изометрлі метрлік кеңістіктер.

Анықтама 2. Егер метірлік кеңістіктерінің өзара бірмәді және үзіліссіз бейнеленуі бар болса, онда бұл бейнелеу гомеоморфизм деп, ал кеңістіктер гомеоморфты деп аталады.

Анықтама 3. Егер кеңістігінің кез келген нүктелерінде теңдігін қанағаттандыратын кеңістігін кеңістігіне өзара бірмәнді f бейнелеуі бар болса, онда бұл кеңістіктер изометрлі деп аталады.

* Толық емес метрикалық кеңістікті толықтау. Метрикалық кеіңстікті толықтау теоремасының дәлелдеуін игеру.

* Бірінің ішңнде бірі орналасқан шарлар туралы теорема.
Осы дәріс бойынша игерілуі тиіс тұжырымдар мен теоремалар:

* определение Фундаменталды тізбектің анықтамасы;

* толық метрикалық кеңістіктің анықтамасы;

* бірінің ішінде бірі орналасқан шарлар туралы теорема;

* қысылу бейнелеудің анықтамасы;

* қысылған бейнелер принципі (Банах теоремасы);

* толық емес метрикалық кеңістіктің толықтамасы;

* толық және толық емес метрикалық кеңістіктердің мысалдары;

* изометрлі метрлік кеңістіктер, мысалдары;

* толық емес метрикалық кеңістікті толықтау процесі.
4-дәріс. Сызықты кеңістіктер

1. Сызықты кеңістіктің анықтамасы.

Сызықты кеңістік деп (СК) элементтерін қосу мен санға көбейту амалдарына қатысты тұйық жиынды айтады. Сонымен (СК): үштігі, осымен қатар қосу амала коммутативті, ассоциативті, СК нөлдік элемент бар: «0» және бұл элемент үшін барлық нүктелерінде (нөлдің бар болуы) және (қарама қарсы элементтің бар болуы).

Элементті санға көбейту мына аксиомаларды мына аксиомларды қанағаттандыруы керек:

.

Егер СК нақты санға көбейту амалы анықталса, онда СК нақты, ал кешен санға көбейту амалы анықталса кешен СК деп аталады

2. СК мысалдары:

1.

3. Изоморфты СК анықтамасы.

және СК изоморфты депаталады, егер осы кеңістіктердің элементтері арасында қосу және санға көбейту амалдарының мәндерін сақтайтын өзара бірмәнді бейнелеу бар болса.

4. Изоморфты СК мысалдары. Мұндай СК қарапайым мысалдарына және әрежесі -ден артық болмайтын көпмүшеліктер кеңістігі жатады.

5. СК сызықты тәуелді элементтер жүйесі.

6. СК сызықты тәуелсіз элементтер жүйесі.

7. СК кеңістіктің өдшемділігі.

8. СК базисі.

9. СК ішкеңістігі.

10. Меншікті ішкеңістік.

11. Меншікті ішкеңістіктің мысалдары.

12. элементтер жүйесінен туындайтын меншікті ішкеңістік. Сызықтық қабықша.

13. Фактор-кеңістік.

14. Сызықты функционал.

15. Сызықты функционалдың геометриялық мағынасы.

Әдебиет (1, Гл. 111,п.1, стр.159-161)

4-дәріс бойынша ОСӨЖ тапсырма: осы дәрістің пункттеріндегі ұғымдарды игеру.

Үшінші тақырыпқа 2 дәріс және 4 жаттығу сабағы жоспарланған

5-дәріс. Нормаланған СК (НЛП). СК элементінің нормасы. Ішкеңістік, оның өлшемділігі. Тізбек элементтерінің нормасы бойынша жинақтылық. Банах кеңістігі. Гельдер және Минковский теңсіздіктері. Банах кеңістіктерінің мысалдары. Лебегтің қосындыланатын функциялар кеңістігі , үзіліссіз функциялар кеңістігінің кеңістігіндегі норма бойынша толықтамасы. Евклид кеңістігі. Гильберт кеңістігі, оның мысалдары. Вектордың ұзындығы, векторлар арасындағы бұрыш. Банах кеңістігінде ортогонал дерлік элементтер жүйесінің бар болатындығы.

Нормаланған СК тақырыбына бір дәрәс және 2 жаттығу сабағы бөлінген.

Осы тақырыл бойынша суденттер білуі керек.

- нормаланған СК ұғымын;

- элементтің нормасын;

- НСК-тегі элементтер тізбегі жинақтылығынын;

- ішкеңістік және оның өлшемділігін;

- Банах кеңістігін;

- Гельдера және Минковский теңсіздіктерін;

- Банах кеңістігінің мысалдарын;

- Лебегтің кеңістіктерін;

- Лебегтің қосындыланатын функциялар кеңістігі , үзіліссіз функциялар кеңістігінің кеңістігіндегі норма бойынша толықтамасы болатындығын;

- Евклид кеңістігін;

- Гильберт кеңістігін;

- вектор ұзындығын;

- векторлар арасындағы бұрыштың анықтамасын және Банах кеңістігінде ортогонал дерлік элементтер жүйесінің бар болатындығын.
6-дәріс. Гильберт кеңістігі. Изоморфизм туралы теорема

Дәріс мазмұны. Гильберт кеңістігінің анықтамасы, мысалдары. Изоморфизм туралы теорема. Ішкеңістік, ортогонал толықтауыш, тура қосынды. Понятия о комплексных Кешен Евклид кеңістігі туралы ұғым (әдебиет 1, 111 т., 6 – 9 пп, стр.180 – 190 беттер).

Анықтама. Шексіз өлшемді толық евклид кеңістігі Гильберт кеңістігі деп аталады.

Толығырақ, жиыны гильберт кеңістігіне айналады, егер бұл жиын скалярлық көбейтінді анықталған, шексіз өлшемді толық кеңістік болса. Изоморфты гильберт кеңістіктері тепе-тең кеңістіктер деп қарастырылады. Гильберт кеңістіктерінің изоморфтылығы бойынша, барлық гиьберт кеістіктері өзара изоморфты болады. бұл теорема барлық гильберт кеңістіктері кеңістігіне изоморфты екендігін көрсету арқылы дәлелденеді. (изоморфизм туралы теорема 1, 181,182 беттер). Бұл теорема толық евклид кеңістігінде орындалатын Рисса-Фишера теоремасына сүйеніп дәелденеді. Гильберт кеңістігіндегі маңызды ұғымдарға ішкеңістік және оның ортогонал толықтауышы жатады. Осы ұғым арқылы гиьберт кеңістігінің кез келген векторы өзара ортогонал ішкеңістіктерде жатқан векторларға жіктеледі. (Бұл теоеманың толық мәтінін оқулықтың 183-187 беттерінен табасыздар). Евклид кеңістігінің сипаттамасы 8-теоремадан (187-191 беттер) табасыздар.

СӨЖ тапсырма. Өздік жұмыста төмендегі ұғымдар мен тұжырымдарды игеру керек:

* Гильберт кеңістігінің анықтамасын;

* Гильберт кеңістігінің мысалдарын;

* Гильберт кеңістіктерінің изоморфтылығы туралы теореманы;

* Гильберт кеңістігінің сепарабельді болатындығы туралы теореманы;

* ішкеңістік және оның ортогонал толықтауышын;

* Гильберт кеңістігінің ортонормаланған ішкеңістіктер жүйесін

* Гильберт кеңістігін ортонормаланған ішкеңістіктердің қосындысы ретінде өрнектеу;

* Евклид кеңістігінің сипаттаыш қасиеті.

Жаттығу сабақтарында 6-дәрістің теориялық материялдары талқыналады.