3. 2 Д_рістер материалдарын о_у_а методикалы_ жетекшілік 1-Та_ыр. 3. 2 Дрістер материалдарын оуа методикалы жетекшілік 1Таырып. Метрикалы кеістіктер
 Скачать 494 Kb. Скачать 494 Kb.
|
|
Төртінші тақырыпқа 2 дәріс және 4 жаттығу сабағы жоспарланған. 7,8-дәрістер. «Сызықты нормаланған метрикалық кеңістіктегі компактылық» тақырыбына екі дәріс төрт жаттығу сабақ бөлінген. Бұл тақырыпта студенттер шенелген, жете шенелген, компакт, шалакомпакакт жиындар туралы ұғымдарды игеруі керек. Бұл тақырыптағы негізгі мәселе метрикалық кеңістіктегі жиындардың компакт немесе шалакомпакакт болу критерийлерін игеру. Осымен қатар, жеке метрикалық кеңістіктегі жиынның компакт болу шарттарын игеру. Жиынның метрикалық кеңістіктегегі компакт болу белгісі – Хаусдорф теоремасы. Бұл жалпылама теореманы жеке қарастырылатын метрикалық кеңістікте қолдану көптеген қиын мәселелерді шешуді керек қылады. Сондықтан жекелеген метрикалық кеңістікте қолдануға қолайлы критерилер қалаптасқан. Мысалы Осы тақырып бойынша студенттер білуі керек: - шенелген және жете шенелген жиындар ұғымын; - метрикалық кеңістіктегі жиынның компакт болу шартын (Хаусдорф теоремасын). - шала компактылық критериін; - жекелеген метрикалық кеңістіктегі жиынның компактылық шарттарын; - Арцел теоремасын; - ақырлы өлшемді кеңістіктегі жиынның компакт болу шартын. Әдебиет: Л. А. Люстерник, В. И. Соболев. Элементы функционального анализа, «НАУКА» М. 1965. (Гл. 5. пп.1, 2, стр. 228-256). Бесінші тақырыпқа 2 дәріс және 4 жаттығу сабағы жоспарланған. 9-дәріс. Сызықты функционалдар. Анықтама 1. Сызықты нормаланған кеңістікте анықталған 1) аддитивті 2) біртекті Функционалдың геометриялық мағынасы (1, стр. 147). Сызықты функционалдың ядросы. Сызықты Тапсырма 1. 2. Покажите, что Анықтама 2. Сызықты нормаланған L кеңістігінде анықталған функционал Анықтама 3. Нормаланған сызықты кеңістікте анықталған Анықтама 4. Сонымен, Сызықты функционал нормасының геометриялық мағынасы Егер Сызықты функционалдың үзіліссіздігі мен шенеулілігі өзара эквиваленті ұғымдар. Теорема 1. Егер сызықты функционал сызықты L кеңістігінің қандайда болмасын бір Теорема 2. Әрбір үзіліссіз функционал шенеулі және шенеулі функционал үзіліссіз болады Хан–Банах теоремасы. Нақты нормаланған сызықты E кеңістігінің сызықты L ішкеңістігінде анықталған шенеулі сызықты СӨЖ тапсырма: * сызықты функционалдың анықтамасы; * сызықты функционалдың ядросы; * сзықты функционалдың геометриялық мағынасы; * * сызықты функционал үзіліссіздігінің анықтамасы; * шенелгендік және үзіліссіздік; * сызықты функционалдың нормасы және оның геометриялық мағынасы; * Берілген сызықты кеңістіктің сызықты ішкеңістігінен берілген кеңістікке дейінгі сызықты функционалдың жалғасы туралы Хан – Банах теремасы. Шешуге ұсынылатын есептер. И.А. Треногин, Б.М. Писаревский, Т.С.Соболева, Задачи и упражнения по функциональному анализу. № 11.2, 11.3, 11.4, 11,5. 10-дәріс. Анықтама. Сызықты Е кеңістігінде анықталған барлық сызықты функционалдар жиыны өз кезегінде сызықты кеңістік болады (дәлелдеңіздер). Бұл кеңістік берілген кеңістікке түйіндес кеңістік деп аталады да, Сонымен, Түйіндес кеңістіктегі норма: Түйіндес кеңістіктегі әлді топология – осы кеңістіктегі топология бойынша жинақтылық. Теорема 1. Түйіндес кеңістік Түйіндес кеңістіктің мысалдары (1, стр. 215 бетке қара). 1-6 мысалдарды игеру керек. Екінші түйіндес кеңістік. Өзіне түйіндес және рефлексивті кеңістіктер. Осындай кеңістіктердің мысалдары. СӨЖ тапсырма: * * * тұйіндес кеңістіктің мысалдары (1-6-шы мысалдар); * екінші түйіндес кеңістік; * өзіне түйіндес және рефлексивті кеңістіктер, мысалдары. Алтыншы тақырыпқа 2 дәріс және 4 жаттығу сабағы жоспарланған Түйіндес кеңістіктің мысалдары. Сызықты функционалдың анықтамасы бойынша, 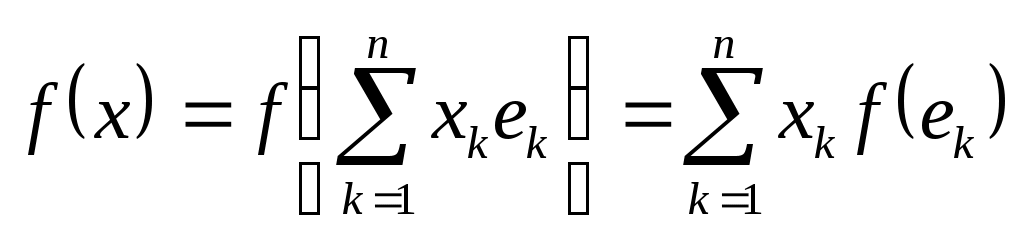 . . 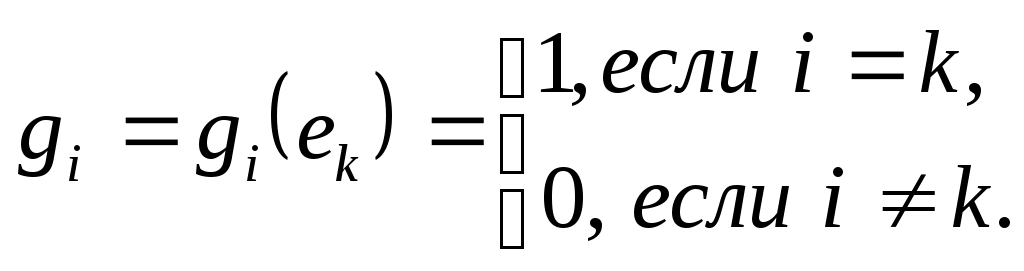 шарттарын қанағаттандыратын сызықты функционалддары үшін шарттарын қанағаттандыратын сызықты функционалддары үшін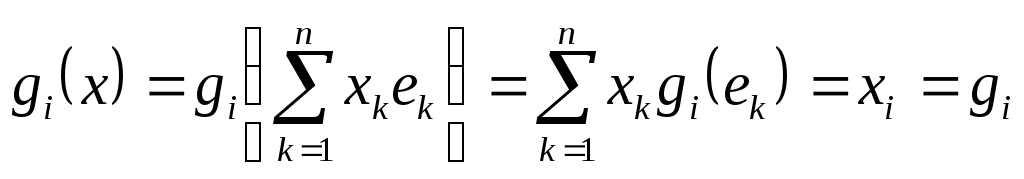 теңдіктері орындалатынын ескеріп, түріне келтіремізде оның нормасын анықтаймыз. Осы мақсатпен, теңсіздігінен төмендегі сұлбаға келеміз: Осымен қатар, Сонымен біз 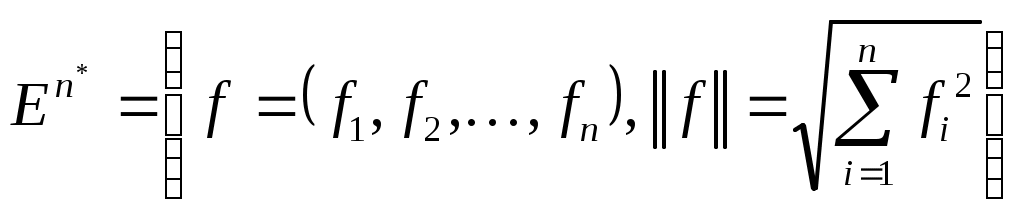 кеңістігіне келеміз. Яғни, кеңістігіне келеміз. Яғни, СӨЖ тапсырма. Әдебиет. Л.А.Люстерник, В.И.Соболев. Элементы функционального анализа. М. 1968, 180-196 беттер. Сегізінші тақырыпқа 2 дәріс және 4 жаттығу сабағы жоспарланған. 12-дәріс. Сызықты операторлар Сызықты оператордың анықтамасы. Айтвлық шартын қанағаттандыратын Оператордың сызықты болатынын дәлелдеу үшін (1) шартының орындалуын тексерсе жеткілікті. 1 – 7 мысалдарын шығару осы шарттың орындалуын тексеруге саяды. Оператордың үзіліссіздігі мен шенеулілігі функционалдың осындай қасиаттарінң ұқсас. Тапсырма 1. Оператордың үзіліссіздігі мен шенеулілігінің анықтамасын жазыңыздар. 2. Сызықты кеңістіктің бір нүктесінде үзіліссіз оператор осы кеңістікте үзіліссіз болатынын дәлелдеңіздер. 3. Сызықты кеңістіктің Операторлардың көбейтіндісі. Операторлар көбейтіндісін анықтау сұлбасы: Белгілеулер : D(A) – А операторының анықталу аймағы, R(A) – А операторының мәндер аймағы, Оператордың нормасы: Сызықты шенеулі операторлар кеңістігі. Сызықты шенелген операторлардың негізгі қасиеттерінің айтылуын В.А Треногиннің есеп кітабынан табасыздар 51, 52 беттер. Осы қасиеттердің дәлелдеулері А.Н.Колмогоров, С.В.Фомин кітабында 251-265 беттер. СӨЖ тапсырма 1. Операторлар арасындағы қосу, санға көбейту, және операторлпрды көбейту амалдарын білу керек.. 2. Шенеулі операторлар кеңістігінің анықтамасын білу керек. осындай кеңістіктің мысыалдарын игеру керек. 3. Шенеулі операторлар кеңістігінің толық болу шартын білу керек. 13-дәріс. Кері оператор, оператордың керіленуі. X кеңістігінен Y кеңістігіне әрекет ететін А операторы берілсін. |
