Ответы на вопросы к экзамену по физике 1 курс 2 семестр.. 1. 1 Молекулярнокинетические и термодинамические методы описания повидения систем
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
|
9.3 уравнение Ван-дер-Вальса и его анализ Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса. Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в более экстремальных условиях её согласие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут. Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, вводящая поправку на конечный диаметр молекулы и на притяжение молекул на больших расстояниях (напомним, что в идеальных газах частицы считаются точечными и никак не взаимодействуют на расстоянии). Реальный газ - газ, в котором учитывается взаимодействие между молекулами. Термическим уравненим состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид: где: P — давление, V — объём, T — абсолютная температура, R — универсальная газовая постоянная, Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает притяжение молекул, поправка b — объём занимаемый молекулами. Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так: 9.3Критическое состояние При некоторой температуре т критическая на изотерме имеется лишь ода точка перегиба, называемая критической точкой,в этой точке касательная к неи параллельна оси абсцисс.Следовательно в этой точке объем и давление называются также критическими. Состояние с критическими параметрами называется критическим состоянием. 9.4 Молекулярные силы взаимодействия. 9.5Внутренняя энергия реальных газов. Внутренняя энергия реальных газов складывается из кинетической энергии теплового движения и потенциальной энергией межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению сил внутреннего давления. P’=a/Vm2 Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, как известно из механики, идет на увеличение потенциальной энергии системы, т.е. δА=р’d Vm =δП δП=а/ Vm2 П=-a/ Vm знак минус означает, что молекулярные силы, создающие внутреннее давление р, являются силами притяжения. Учитывая оба слагаемы, получаем,что внутренняя энергия моля реального газа Um = CvT- a/ Vm 9.6Эффект Джоуля - Томсана Эффе́ктом Джо́уля-То́мсона называется изменение температуры газа при адиабатическом дросселировании(расширении) — медленном протекании газа под действием постоянного перепада давлений сквозь дроссель, местное препятствие газовому потоку. Данный эффект является одним из методов получения низких температур. Эффект Джоуля-Томсона называется положительным, если газ в процессе дросселирования охлаждается и отрицательным, если нагревается. U2-U1=A’ U2-U1=p1V1-p2V2 U2+p2V2 = U1+p1V1 Знак эффекта Джоуля-Томсона меняется при температуре инверсии. Как это следует из закона сохранения энергии, а также из того что рассматриваемый процесс протекания медленный, в процессе Джоуля-Томсона остается постоянной энтальпия (изоэнтальпийный процесс). Для идеального газа, в отличие от реального, условие изоэнтальпийности дает нулевое изменение температуры и для него эффект отсутствует. 9.7 Сжижение газов переход вещества из газообразного состояния в жидкое. С. г. достигается охлаждением их ниже критической температуры (Тк) и последующей конденсацией в результате отвода теплоты парообразования (конденсации). Охлаждение газа ниже ТК необходимо для достижения области температур, при которых газ может сконденсироваться в жидкость (при Т > ТК жидкость существовать не может). 10.1 Агрегатные состояния вещества. Газы. Жидости. Кристаллически твердые тела. Агрега́тное состоя́ние — термодинамическое состояние вещества, сильно отличающееся по своим физическим свойствам от других агрегатных состояний этого же вещества. Агрегатное состояние определяется физическими условиями, в которых находится вещество, главным образом температурой и давлением. твёрдое тело (аморфное либо кристаллическое), держит как форму, так и объём. Криста́ллы (от греч. κρύσταλλος, первоначально — лёд, в дальнейшем — горный хрусталь, кристалл), твёрдые тела, в которых атомы расположены закономерно, образуя трёхмерно-периодическую пространственную укладку — кристаллическую решётку. Ам́орфные веществ́а (от др.-греч. ἀ «не-» и μορφή «вид, форма») не имеют кристаллической структуры и в отличие от кристаллов не расщепляются с образованием кристаллических граней, как правило — изотропны, то есть не обнаруживают различных свойств в разных направлениях, не имеют определенной точки плавления жидкость, характеризуется более низкой плотностью и промежуточными температурами. Жидкость держит объём, но не держит форму. газообразное состояние, характеризуется низкой плотностью и достаточно высокой температурой. Газ не держит ни форму, ни объём. 10.2 Фазовое равновесие и превращения Равнове́сие фаз в термодинамике — состояние, при котором фазы в термодинамической системе находятся в состоянии теплового и механического равновесия. Типы фазовых равновесий: Тепловое равновесие означает, что все фазы вещества в системе имеют одинаковую температуру. Механическое равновесие означает равенство давлений по разные стороны границы раздела соприкасающихся фаз. Строго говоря, в реальных системах эти давления равны лишь приближенно, разность давлений создается поверхностным натяжением. 10.3 Фазовые переходы первого рода Фазовый переход-переход вещества из одной фазы в дргую. Фазовый переход первого рода (плавление, кристаллизация) сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода. Фазовые переходы первого рода характеризуются постоянством температуры, изменениями энтропии и объема. 11.1 Кривая фазового равновесия Для наглядного изображения фазовых превращений используется диаграмма состояния, на которой в координатах р, Т задается зависимость между температурой фазового перехода и давления в виде кривых испарении (Ки), плавления (Кп) и сублимации(Кс), разделяющих поле диаграммы на три области , соответствующие условиям существования твердой (тт), жидкой (ж) и газообразной (г) фаз. Кривые на диаграмме называются кривыми фазового равновесия, каждая точка на них соответствует условиям равновесия двух существующих фаз: КП твердого тела и жидкости, КИ жидкости и газа, КС жидкости и газа.  11.2Тройная точка - точка, в которой пересекаются кривые фазового равновесия, называется тройной точкой. Она определяет условия одновременного равновесного существования трёх фаз вещества. 11.3 Закон Клапейрона-Клаузиуса КЛАПЕЙРОНА-КЛАУЗИУСА УРАВНЕНИЕ, устанавливает связь между изменениями равновесных значений т-ры Т и давления р однокомпонентной системы (чистого в-ва) при фазовых переходах первого рода (плавлении, испарении, сублимации, полиморфных превращениях). Имеет вид: где DV - изменение объема системы при фазовом переходе, L - теплота перехода. При равновесном переходе 1 моля в-ва из фазы 1 в фазу 2 при постоянных T и p (процесс изотермо-изобарический) L=H2-Н1 и DV=V2-Vl, где Н2, Hl, V2 и Vl - молярные энтальпии и объемы фаз 1 и 2 соответственно. Производная dp/dT рассчитывается как тангенс угла наклона касательной к кривой сосуществования фаз на фазовой р-Т диаграмме. При рассмотрении испарения и сублимации К.-клапейрона-клаузиуса уравнение обычно используют для изучения влияния т-ры на равновесное давление пара над жидкостью или твердым в-вом (определяют dp/dT); обратная величина dT/dp описывает влияние давления на т-ру кипения или сублимации. 12.1 Строение и свойства жидкостей Форма жидких тел может полностью или отчасти определяться тем, что их поверхность ведёт себя как упругая мембрана. Так, вода может собираться в капли. Но жидкость способна течь даже под своей неподвижной поверхностью, и это тоже означает несохранение формы (внутренних частей жидкого тела). Молекулы жидкости не имеют определённого положения, но в тоже время им недоступна полная свобода перемещений. Между ними существует притяжение, достаточно сильное, чтобы удержать их на близком расстоянии Свойства: Текучесть Сохранение объёма Вязкость Образование свободной поверхности и поверхностное натяжение Испарение и конденсация Кипение Смачивание Смешиваемость Диффузия 12.2Поверхностный слой Если жидкая и газообразная фазы одного и того же вещества соприкасаются, возникают силы, которые стремятся уменьшить площадь поверхности раздела — силы поверхностного натяжения. Поверхность раздела ведёт себя как упругая мембрана, которая стремится стянуться. Поверхностное натяжение может быть объяснено притяжением между молекулами жидкости. Каждая молекула притягивает другие молекулы, стремится "окружить" себя ими, а значит, уйти с поверхности. Соответственно, поверхность стремится уменьшится. 12.3 Поверхностная энергия Для перемещения молекулы из глубины жидкости в поверхностный слой надо затоту. Эта работа совершается за счет кинетической энергии молекул и идет на увеличение их потенциалной энергии. Поэтому молекулы поверхностного слоя Жидкости обладают большей потенциальной энергией, чем молекулы внутри жидкости. Эта дополнительная энергия,которой обладают молекулы в поверхностном слое жидкости, называется поверхностной энергией, пропорционально площади слоя ДельтаЕ=сигма*дельтаS 12.4 Явление смачивания Смачивание Смачивание - поверхностное явление, возникающее при контакте жидкости с твёрдой поверхностью в присутствии пара, то есть на границах раздела трёх фаз. Смачивание характеризует "прилипание" жидкости к поверхности и растекание по ней (или, наоборот, отталкивание и нерастекание). Различают три случая: несмачивание, ограниченное смачивание и полное смачивание.  12.5 Формула Лапласа   12.6 Капилярные явления  12.7 Адсорбция. Адсорбция— процесс концентрирования вещества из объёма фаз на границе их раздела. Физическая адсорбция Причиной адсорбции являются неспецифические (то есть не зависящие от природы вещества) ван-дер-ваальсовы силы. Адсорбция, осложненная химическим взаимодействием между адсорбентом и адсорбатом, является особым случаем. Явления такого рода называют хемосорбцией и химической адсорбцией. «Обычную» адсорбцию в случае, когда требуется подчеркнуть природу сил взаимодействия, называют физической адсорбцией. Количественно процесс физической мономолекулярной адсорбции в случае, когда межмолекулярным взаимодействием адсорбата можно пренебречь, описывается уравнением Ленгмюра: где θ — доля площади поверхности адсорбента, занятая адсорбатом, α — адсорбционный коэффициент Ленгмюра, а P — концентрация адсорбтива. Поскольку [S − P] = θ и, соответственно, [S * ] = 1 − θ, уравнение адсорбционного равновесия может быть записано следующим образом: 12.8 Сжимаемость и тепловое расширение СЖИМАЕМОСТЬ (объемная упругость), способность в-ва обратимо изменять свой объем под действием равномерного всестороннего давления. Характеризуется коэффициентом сжимаемость b, определяемым как относит. изменение объема V (или плотности р) в-ва с изменением давления р: Тепловое расширение — изменение линейных размеров и формы тела при изменении его температуры. Количественно тепловое расширение при постоянном давлении характеризуется изобарным коэффициентом расширения (объёмным коэффициентом теплового расширения). Для характеристики теплового расширения твердых тел дополнительно вводят коэффициент линейного теплового расширения. Основной закон теплового расширения гласит, что тело с линейным размером L в соответствующем измерении при увеличении его температуры на ΔТ расширяется на величину ΔL, равную: ΔL = αLΔT де α — так называемый коэффициент линейного теплового расширения. 12.9 Ближний порядок в жидкостях  Электростатика. 13.1 Электростатическое поле.  13.3 закон сохранения электрического заряда.  13.4 Закон кулона   13.5 Напряженность и потенциал     13.6 Энергия заряженного тела в электростатическом поле. 13.7 Принцип суперпозиции при расчёте характеристик полей.  13.8 Связь между напряженность и Потенциалом поля   Графическое изображение электростатического поля (Эквипотенциальные поверхности, силовые линии)   14.1Распределяемые заряды и их характеристики: лин. Пов. Об. Пло-ти. Линейная плотность электрического заряда — предел отношения электрического заряда, находящегося в элементе линии, к длине этого элемента линии, который содержит данный заряд, когда длина этого элемента стремится к нулю. Поверхностная плотность электрического заряда — предел, к которому стремится отношение электрического заряда к площади, на которой этот заряд расположен, при условии что эта площадь стремится к нулю. Объемная плотность плотность=q/V q=ро4/3пи*R3 14.2ма Остраградского – Гаусса   Поле двух параллельных разноименно заряженных плоскостей. Поле разноименно заряженной сферической поверхности  Поле объемно заряженного шара 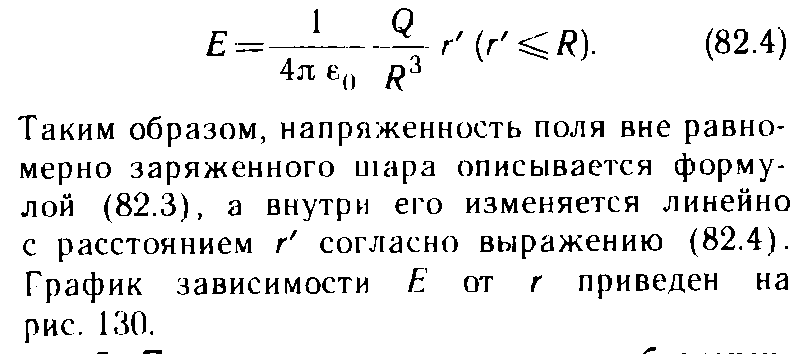 Поля бесконечно заряженного цилиндра(нити) 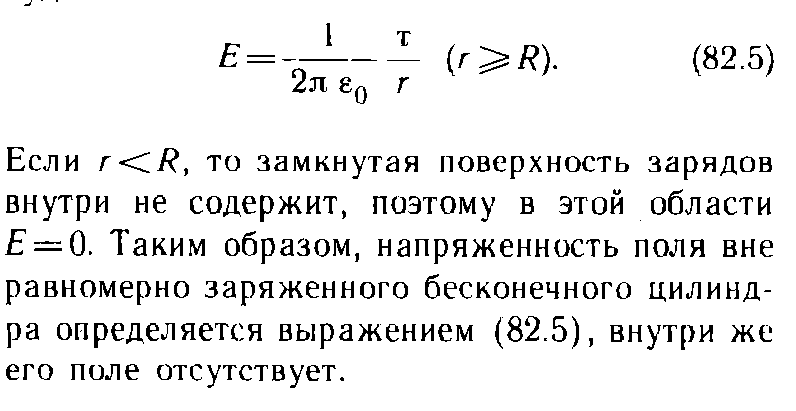 15.1 Потенциальный характер электростатического поля. Работа сил при перемещении зарядов. 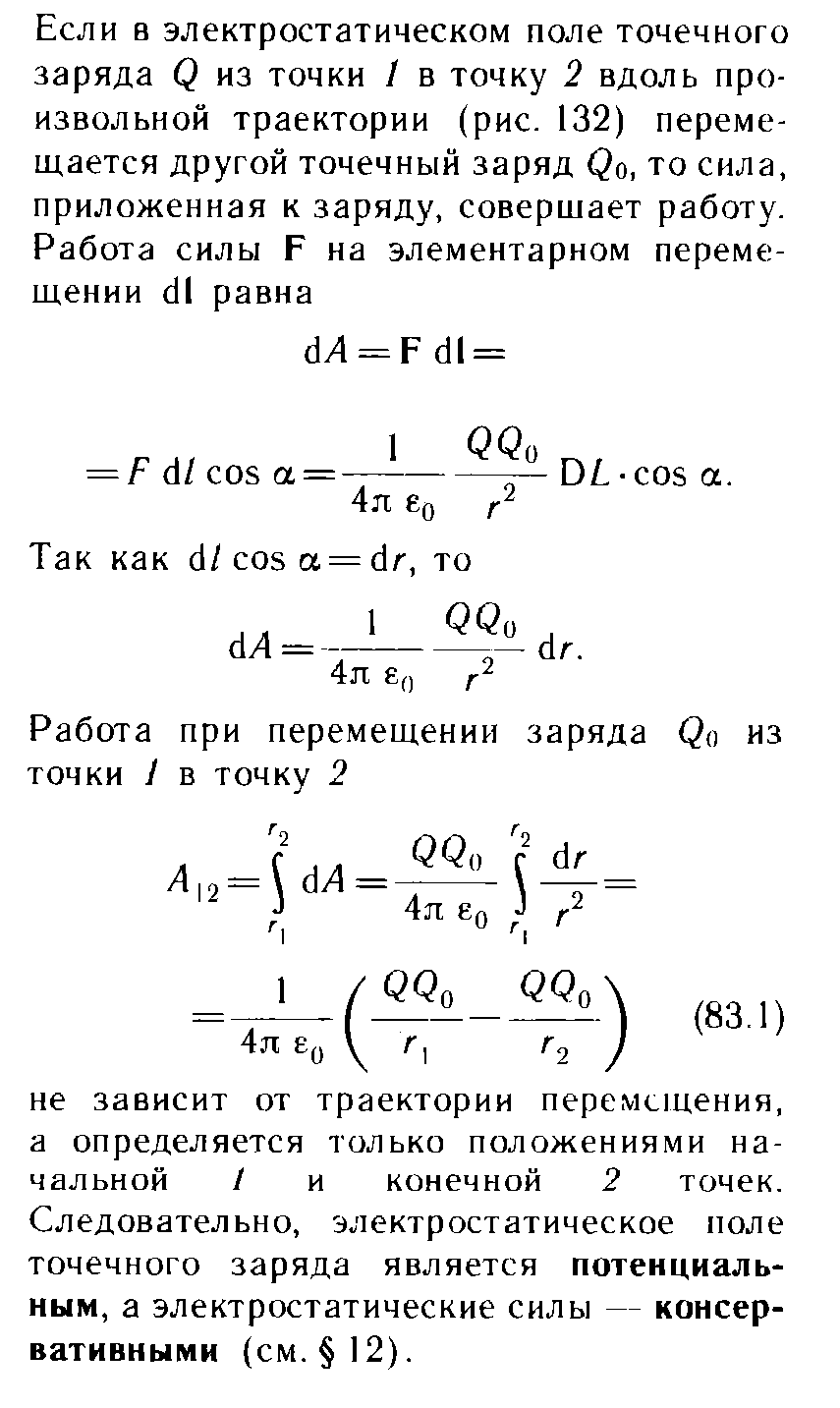 15.2 Циркуляция Теорема о циркуляции вектора напряженности электрического поля  15.3 проводнике во внешнем электрическом поле  Равновесие зарядов на проводнике 1)Напряженность поля внутри проводника равна нулю 2)напряженность на поверхности в каждой точке направлена по нормали к повнрхности. E=En 16.1Электроемкость Электроекость – характеристика проводника, его способность удерживать электрический заряд. Это коэф. пропорциональности между потенциалом и зарядом Зависит от формы, размеров проводника и диэлектрической проницаемости среды. Теплоемкость шара 16.2 Конденсаторы   16.3оединения конденсаторов Емкость плоского коненсатора Последовательное соединение Параллельное соединение 16.4ия электрического поля 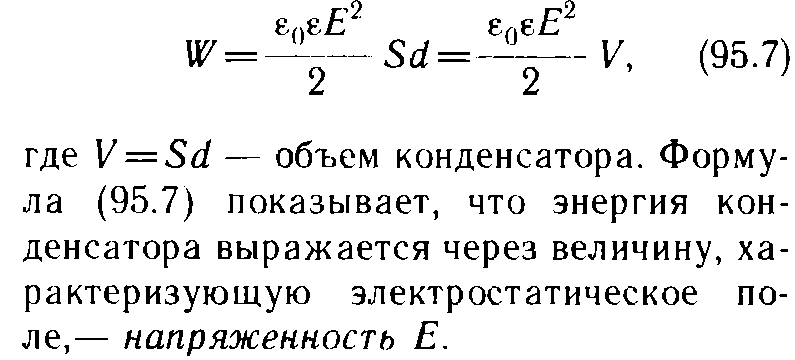 Объемная плотность Если поле однородное,то заключенная в нем энергия распред. В пространстве с пост. Плотностью омега, равная энергия поля деленная на занимаемый полем объем 17.1Электрическое поле в веществе. Типы диэлектриков 1)неполярные молекулы совпадают положительные и отрицательные центры тяжести 2)полярные молекулы положительные и отрицательные центры тяжести не совпадают 3)ионные кристаллы если диэл помещены в Эл. поле, то на границе диэл. Возникают связанные заряды. Поля в диэлектриках описываются с помощью вектора поляризации. Диэликтрическая восприимчивость вещества. Электрическое смещение  Условия на границе двух диэлектриков   Сегнотоэлектрики  |
