1 Методи та механізми 2014. 1. 1 Основні послуги при застосуванні, уніфікація та стандартизація криптографічних перетворень
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
|
повинна використовуватися тільки для цифрових підписів, але не для інших цілей (наприклад, направленого шифрування чи встановлення ключів). Вимоги до захисту ключів та загальних параметрів в достатній мірі викладені надається в NIST SP 800-57. З урахуванням вимог, що викладені в NIST SP 800-57 та FIPS 186-3 [218] , довжини модулів (nlen) повинні бути 2048 і 3072 та більше бітів. Також повинна використовуватись затверджена геш - функція, з параметрами як визначено в FIPS 180-3 та ДСТУ ISO/IEC 10118 -3 [ 194]. Тобто, криптографічна геш-функції повинна відповідати або перевищувати стійкість, яка визначається довжиною модуля RSA криптографічного перетворення N. Краще, щоби стійкість захисту модуля N і геш - функції бути однаковими, якщо тільки не вимагається інше. Також RSA тобто, прості числа P і Q, а також експонента відкритого ключа 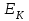 повинні генеруватися з використанням затвердженого генератора випадкових або псевдовипадкових чисел, наприклад згідно NISN SP 800-90 та ДСТУ ISO/IEC 18031-1. При цьому результуючі (псевдо) випадкові числа повинні використовуватися для генерації RSA параметрів як початкові числа. Початкові числа генерації простих чисел повинні триматися в таємниці, або знищуватись, коли обчислюється модуль N. У випадку зберігання початкових чисел генерації простих чисел, вони повинні використовуватися тільки як свідоцтво того, що генеровані значення (тобто, p, q або e) були визначені довільним чином і повинні бути захищені як мінімум так , як вимагається для особистого ключа. повинні генеруватися з використанням затвердженого генератора випадкових або псевдовипадкових чисел, наприклад згідно NISN SP 800-90 та ДСТУ ISO/IEC 18031-1. При цьому результуючі (псевдо) випадкові числа повинні використовуватися для генерації RSA параметрів як початкові числа. Початкові числа генерації простих чисел повинні триматися в таємниці, або знищуватись, коли обчислюється модуль N. У випадку зберігання початкових чисел генерації простих чисел, вони повинні використовуватися тільки як свідоцтво того, що генеровані значення (тобто, p, q або e) були визначені довільним чином і повинні бути захищені як мінімум так , як вимагається для особистого ключа. Детальні вимоги до генерування загальних параметрів та асиметричних пар RSA ключів наведено в [265]. Також необхідно враховувати, що відносно RSA вимоги ззмінюються часто, що потрібно відслідковувати та корегувати вимоги. ANS X9.31, Цифрові Підписи з Використанням Оборотної Криптографії Відкритого Ключа для Індустрії Фінансових Послуг (rDSA), розроблений для Національного Інституту Стандартизації Сполучених Штатів Акредитованим Комітетом Стандартів по Фінансовим Послугам, X9. Інформація про отримання копій ANS X9.31 доступна на http://www.x9.org Список друкарських помилок для ANS X9.31 також доступний. Наступні обговорення засновані на версії ANS X9.31, яка була затверджена в 1998 р.. 1.10.2 Перелік, сутність, вимоги та стан стандартизації методів побудування загально - системних параметрів для криптографічного перетворення в скінченному полі. Перед безпосереднім застосуванням криптографічного перетворення направленого шифрування в скінченному полі(Галуа), кожному користувачеві попередньо необхідно генерувати загальні параметри та асиметричну ключову пару - ключ. Як і в RSA криптографічному перетворенні , перетворення в скінченному полі може застосовуватись як для електронного підпису, так і для направленого шифрування[ 20-23, 18032]. Для направленого шифрування з гідно [ 18032, 20-23] генерування загальних параметрів та ключа повинне здійснюватись таким чином. Нехай є скінченне поле (Галуа) F(p). Спочатку третя довірена сторона генерує загальні параметри 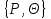 , де , де 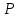 - просте, як правило «сильне» просте число, а - просте, як правило «сильне» просте число, а 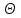 - первісний елемент. Загально - системні параметри повинні розповсюджуватись в домені та встановлюватись і використовуватись на встановленому інтервалі часу з забезпеченням послуг безпеки - тобто забезпечення їх цілісності, справжності, доступності , неспростовності та надійності. - первісний елемент. Загально - системні параметри повинні розповсюджуватись в домені та встановлюватись і використовуватись на встановленому інтервалі часу з забезпеченням послуг безпеки - тобто забезпечення їх цілісності, справжності, доступності , неспростовності та надійності.Далі всі користувачі домену повинні генерувати по принципу « сам – собі» 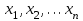 - особисті(таємні) ключі і зберігати та використовувати відповідним чином, причому , де - особисті(таємні) ключі і зберігати та використовувати відповідним чином, причому , де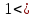 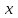 i i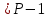 . (1.192) . (1.192)Відкриті ключі кожен користувач обчислює, використовуючи справжні загальносистемні діючі параметри 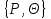 у вигляді відповідного елемента скінченного поля, тобто у вигляді відповідного елемента скінченного поля, тобто 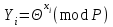 (1.193) (1.193) Приклад генерування асиметричних пар ключів для двох користувачів наведений в таблиці 1.29 Таблиця 1.29 - Генерування асиметричної пари ключів у скінченному полі
Основними вимогами до загально - системних параметрів направленого шифрування в скінченному полі такі[ 218, 20-21]: при зашифруванні та розшифруванні повинні використовуватись цілісні, справжні доменні та доступні загально - системні параметри 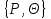 , одинакові для усіх користувачів домену; , одинакові для усіх користувачів домену;асиметрична пара - ключ {хi, Уi) повинна генеруватись на основі випадкового (псевдовипадкового) особистого ключа хi, що задовольняє вимозі (1.192) та обчислення відкритого згідно (1.193); зашифрування повинне здійснюватись за допомогою відкритого ключа Уi, а перевіряння за допомогою особистого ключа хi.. Електронний підпис в скінченному полі здійснюється на основі криптографічного перетворення Ель-Гамаля за двома модулями – простими числами P та q. Загальносистемними параметрами з урахуванням є Таблиці 1.30 - загальні параметри електронного підпису в скінченному полі
Указані загальносистемні параметри можуть бути для всіх користувачів однаковими і змінюватися дуже рідко. У FIPS 186-1 обмеження на загальні параметри інші, їх можна знайти в [219]. До загально - системних параметрів та ключів електронного підпису в скінченному полі (FIPS 186 - 1 та FIPS 186 - 3(DSA)) повинні виконуватись такі вимоги: - P - простий модуль, де 2L-1 < P< 2L, і L - бітова довжина P. Значення для L надаються в [218 ]; - q - простий дільник (p- 1), де 2N-1 < q < 2 N, і N - бітова довжина q. Значення для N надаються в [218 ]; g - генератор підгрупи порядку q mod P, такий, що 1 < g < q. x - особистий (таємних )ключ, який повинен бути випадковим або псевдовипадковим цілим числом, таким, що 0 < x < q, тобто, x знаходиться в діапазоні цілих чисел [1, q-1]. Y- відкритий ключ, причому 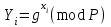 . .Згідно вимог FIPS 186 - 3(DSA) варіанти для пари L і N (бітові довжини p і q,відповідно) повинні задовільняти таким вимогам: (L = 2048, N = 224 ) або (L = 2048, N = 256) або (L = 3072, N = 256). Основними, крім названих вище, для загальних параметрів та ключів повинні виконуватись такі вимоги [218]: стійкість захисту геш - функції, що застосовується, повинна відповідати або перевищувати стійкість захисту (L, N); починаючи з 2012 року повинні використовуватись тільки перші дві (L, N) пари (тобто, (2048, 224) і (2048, 256) пари; загальні (доменні) параметри можуть бути загальними для групи користувачів і можуть бути відкритими; асиметрична пара - ключ {хi, Уi) повинна генеруватись на основі випадкового (псевдовипадкового) особистого ключа хi, що задовольняє вимозі (1.192) та обчислення відкритого згідно (1.193); відносно загальних параметрів повинні виконуватись вимоги відносно їх цілісності, справжності, доступності , неспростовності та надійності ; набір загально системних (доменних) параметрів може залишатися фіксованим протягом тривалого періоду часу; доменними параметрами для DSA електронного підпису є цілі числа p, q, і g; доменні параметри можуть бути генеровані довіреною третьою стороною (такою як CA) або іншим об’єктом; гарантія справжності доменного параметра повинна бути отримана перед генерацією ключової пари, виробленням або перевірянням електронного підпису; загально - системні параметри повинні бути захищені від несанкціонованої модифікації, а також можуть використовуватися тільки для однієї мети (наприклад, для електронного підпису, направленого шифрування чи встановлення ключів); особистий ключ повинен використовуватися тільки протягом фіксованого періоду часу (тобто, крипто періоду особистого ключа); відкритий ключ може використовуватися, поки є необхідність перевіряння електронних підписів, генерованих з використанням зв'язаного з особистим ключем; особистий ключ повинен бути захищений від несанкціонованого доступу, розкриття і модифікації; відкритий ключ повинен бути захищений від несанкціонованої модифікації (включаючи заміну), наприклад,при використанні сертифіката відкритого ключа; A. перевірник повинен бути упевнений в наявності зв'язку між відкритим ключем, його зв'язаними доменними параметрами і власником ключової пари ; - перевірник повинен отримати відкриті ключі довіреним шляхом (наприклад, із сертифікату). Деталізацію вимог до електронного підпису можна знайти в [20-22 ], але потрібно враховувати, що вони змінюються з часом. 1.10.3 Перелік, сутність, вимоги та стан стандартизації методів побудування загально - системних параметрів для криптографічного перетворення в групі точок еліптичних кривих. 1.10.3.1 Загальні параметри еліптичних кривих над полями 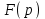 При обґрунтуванні вимог до побудування загальних параметрів еліптичних кривих в якості основних будемо використовувати такі джерелах [268,51-52, 20-21, 218, 234, 265]. Згідно вказаних джерел до загальних параметрів еліптичної кривої Енад полем 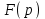 належать такі параметри: належать такі параметри:Розмір поля 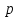 , який визначає базове кінцеве поле , який визначає базове кінцеве поле 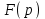 , де , де 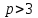 повинно бути простим числом. повинно бути простим числом.Параметри 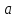 та та 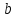 еліптичної кривої, які визначають рівняння еліптичної кривої еліптичної кривої, які визначають рівняння еліптичної кривої 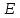 , що використовується: , що використовується: 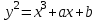 . .Базова точка 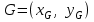 порядку порядку  з координатами з координатами 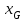 та та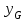 . .Порядок  базової точки базової точки 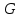 за умови, що за умови, що 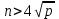 та та  – просте число. – просте число.Кофактор 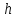 взаємозв’язку порядку кривої взаємозв’язку порядку кривої 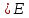 та порядку базової точки та порядку базової точки  , причому , причому 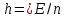 . .Бітовий рядок 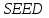 , якщо еліптична крива генерована випадково. У [267,268] наведено приклад того, як генерувати випадкову еліптичну криву та контролювати її параметри, використовуючи для ініціалізації рядок , якщо еліптична крива генерована випадково. У [267,268] наведено приклад того, як генерувати випадкову еліптичну криву та контролювати її параметри, використовуючи для ініціалізації рядок 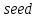 (необов’язково). (необов’язково).Крива, тобто її параметри 1–6, ні в якому разі не повинні вибиратись із переліку значень, що виключені зі списку (не рекомендуються або заборонені). З використанням вказаних джерел можна сформулювати вимоги до розміру та властивостей загальних параметрів еліптичних кривих. Сутність цих вимог у наступному[ 267 ]. Порядок кривої 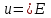 , порядок , порядок  базової точки базової точки 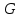 еліптичної кривої та модуль перетворення еліптичної кривої та модуль перетворення 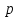 взаємопов’язані: взаємопов’язані: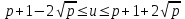 (1.194) (1.194)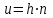 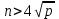 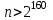 В цілому маємо: 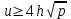 (1.195) (1.195)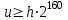 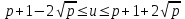 Співвідношення (1.194)–(1.192) дозволяють вибрати вказані загальні параметри ЕК. 1.10.3.2. Методи побудови загальних параметрів еліптичних кривих над полем 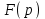 Аналіз основних доступних джерел показав, що методи побудови загальних параметрів еліптичних кривих можна розділити на 2 групи: методи, що ґрунтуються на побудові загальних параметрів вибраного порядку підгрупи базової точки, на основі якого обчислюються параметри кривої. В якості прикладу є метод „ комплексного множення ” [268]; методи обчислення порядку кривої, параметри якої вибрані випадково. До них належать метод Скуфа, SEA та метод «Великих і малих кроків» [51, 52, 20, 21, 268]. Методи комплексного множення мають такі обмеження й недоліки[37, 268]: порядок еліптичної кривої обчислюється попередньо та не є випадковим; обмежене число кривих, що можуть використовуватися; взаємна пов’язаність параметрів еліптичної кривої між собою; значна складність обчислення кореня поліному, причому максимально допустиме значення поліному не перевищує 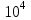 ; ;обмеженість загальних параметрів значенням дискримінанти кривої. Зважаючи на вказане, метод комплексного множення використовувати не рекомендується. Методи побудови загальних параметрів з використанням випадково генерованої кривої зводяться до перевірки параметрів кривої та обчисленню порядку такої кривої. Вони практично не мають вказаних для «комплексного множення» недоліків, але є біль складними та вимагають значно більших обчислювальних ресурсів. Серед цих методів необхідно виділити метод Скуфа, що має поліноміальну складність генерування параметрів кривої, а також алгебро - геометричний метод. Метод Скуфа у подальшому був удосконалений Алкіном та Елкістом, що дозволило суттєво знизити складність його реалізації. Так, складність алгоритму Скуфа складає 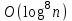 . (1.196) . (1.196)Складність вдосконаленого методу (SEA) можна оцінити як 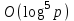 (1.197) (1.197)У цілому проведені дослідження дозволяють зробити такі висновки: при виборі випадково вибраної еліптичної кривої забезпечується формування криптографічно стійких загальних параметрів; алгоритм Скуфа забезпечує обчислення порядку будь-якої кривої як над простим так і над розширеним полем, але обчислювальна складність при цьому зростає зі збільшенням 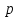 поліноміально; поліноміально;алгоритм SEA має суттєво меншу складність обчислення порядку випадково генерованих еліптичних кривих; Таким чином, на теперішній час розроблено та реалізовано метод побудови параметрів еліптичних кривих SEA, що задовольняє вимогам щодо криптографічної стійкості та має допустиму складність для кривих з порядком до 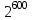 . .1.10.3.3. Загальні параметри еліптичної кривої над полем 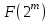 До загальних параметрів еліптичної кривої над скінченним полем 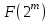 необхідно віднести такі параметри[191]. необхідно віднести такі параметри[191].Розмір поля 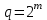 , який визначає базове скінченне поле , який визначає базове скінченне поле 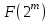 і є покажчиком базису, що використовується для подання елементів поля. і є покажчиком базису, що використовується для подання елементів поля.Параметри 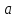 та та 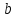 еліптичної кривої, які визначають рівняння еліптичної кривої еліптичної кривої, які визначають рівняння еліптичної кривої 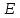 , що використовується : , що використовується : 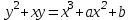 . .Базова точка 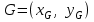 порядку порядку  з координатами з координатами 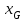 та та 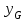 . .Порядок  базової точки базової точки 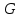 при умові, що при умові, що 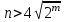 та та  – просте число. – просте число.Кофактор 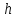 взаємозв’язку порядку кривої взаємозв’язку порядку кривої 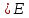 та порядку базової точки та порядку базової точки  причому причому 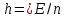 (не обов¢язково, якщо це потрібно в базовій схемі). (не обов¢язково, якщо це потрібно в базовій схемі).Крива, тобто її параметри 1-6, ні в якому разі не повинні вибиратись із переліку значень, що виключені із списку (не рекомендуються або заборонені). Бітовий рядок 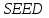 , якщо еліптична крива генерована випадково. В [268] наведено приклад того, як згенерувати випадкову еліптичну криву та контролювати її параметри, використовуючи для ініціалізації строку , якщо еліптична крива генерована випадково. В [268] наведено приклад того, як згенерувати випадкову еліптичну криву та контролювати її параметри, використовуючи для ініціалізації строку 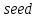 (необов’язково). (необов’язково).Із [191] можна зробити висновок, що на цей час розроблено й рекомендовано до використання такі еліптичні криві над скінченним полем 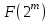 зі значенням зі значенням 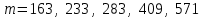 . Для вказаних значень m можуть використовуватись тільки поліноми . Для вказаних значень m можуть використовуватись тільки поліноми 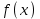 , що мають вигляд: , що мають вигляд: f (x) = 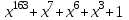 ; ;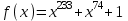 ; ;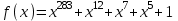 ; (1.198) ; (1.198)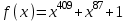 ; ;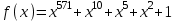 . .Необхідно зазначити, що при використанні пентаномів, тобто поліномів із п’ятьма членами, у порівнянні з трьома, збільшується складність криптоперетворень. Для вказаних m порядок скінченного поля вибраний таким чином, щоб його довжина була у два рази більшою за довжини ключів для симетричних шифрів. При таких співвідношеннях забезпечується однаковий рівень стійкості симетричного шифру та криптоперетворень у групі точок еліптичних кривих. У [191] наведено параметри еліптичних кривих 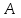 , , 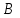 та та  для еліптичних кривих у поліноміальному базисі ( для еліптичних кривих у поліноміальному базисі (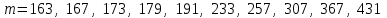 ) та оптимальному нормальному базисі ( ) та оптимальному нормальному базисі (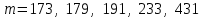 ). ).Із наведеного вище можна зробити висновок, що на теперішній час розроблено методи та засоби обчислення загальних параметрів. Існує можливість використання як уже сформованих і поданих у стандартах [234, 265, 218] загально - системних параметрів, так і їх формування з використанням методів Скуфа і Сатоха [52]. Враховуючи складність формування загально - системних параметрів, можна рекомендувати використовувати загальні параметри, що наведені в [191,234, 265]. У подальшому мають бути розроблені спеціальні програмно-апаратні комплекси, що призначені для формування загальних параметрів еліптичних кривих. На наш погляд, в першу чергу потрібно провести детальний аналіз, розглянути та обгрунтувати з урахуванням перспективних вимог, розміри загально - системних параметрів, а також прийняти в якості національного стандарту та введення в дію міжнародного стандарту ISO/IEC 15946 - 5. Наступним кроком є удосконалення стандарту ISO/IEC 15946 - 5, в першу чергу в напряму збільшення порядків базових точок, включно до n =21024, та можливо і більше. Перспективним також є алгебро - геометричний метод [412 ]. При його застосуванні можна значно зменшити складність, і , як правило, підвищити швидкодію. 1.10.3.4. Методи побудови загальних параметрів еліптичних кривих над полем 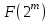 На цей час найбільш придатним методом формування загальних параметрів у групі точок виконуються у два етапи[ 52 ]: 1) підняття циклу ізогенії та коефіцієнтів кривої; 2) обчислення сліду ендоморфізму Фробеніуса, на базі якого визначається порядок кривої. Підняття виконується послідовним підняттям 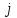 - інваріантів, коефіцієнтів кривої разом з підняттям еліптичних кривих над полем - інваріантів, коефіцієнтів кривої разом з підняттям еліптичних кривих над полем 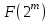 є метод Сатоха [20-21? 52]. є метод Сатоха [20-21? 52].Метод Сатоха, як і метод Скуфа, для визначення порядку кривої використовує властивості ендоморфізму Фробеніуса, але ідея алгоритму серйозно відрізняється від алгоритму Скуфа. Обчислення підгруп 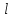 - крутіння з попереднім обчисленням циклу кривих та - крутіння з попереднім обчисленням циклу кривих та 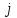 - інваріантів - інваріантів 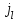 . . Для зниження обчислювальних затрат підняття виконується з використанням багатомірної ітерації Ньютона, що дозволяє виконати одночасний підйом. Це дозволяє обчислити спряжені 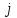 -інваріанти -інваріанти 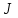 , не обчислюючи значення ендоморфізму Фробеніуса. , не обчислюючи значення ендоморфізму Фробеніуса.1.10.3.5 Загальні параметри еліптичних кривих над полями та 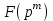 До загальних параметрів еліптичної кривої над полем 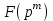 належать такі параметри: належать такі параметри:розмір поля 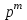 , який визначає базове кінцеве поле , який визначає базове кінцеве поле 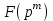 , де , де 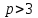 має бути простим числом; має бути простим числом;бітовий рядок 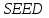 , якщо еліптична крива генерована випадково. У [265,267, 268] наведено приклад того, як згенерувати випадкову еліптичну криву та контролювати її параметри, використовуючи для ініціалізації строку , якщо еліптична крива генерована випадково. У [265,267, 268] наведено приклад того, як згенерувати випадкову еліптичну криву та контролювати її параметри, використовуючи для ініціалізації строку 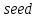 (необов’язково); (необов’язково);параметри 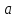 та та 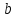 еліптичної кривої, які визначають рівняння еліптичної кривої еліптичної кривої, які визначають рівняння еліптичної кривої 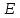 , що використовується: , що використовується: 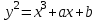 ; ;базова точка 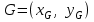 порядку порядку  з координатами з координатами 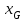 та та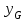 ; ;порядок  базової точки базової точки 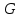 за умови, що за умови, що 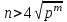 та та  – просте число; – просте число;кофактор 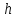 взаємозв’язку порядку кривої взаємозв’язку порядку кривої 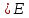 та порядку базової точки та порядку базової точки  причому причому 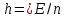 . .При цьому еліптична крива, тобто її параметри, ні в якому разі не повинні вибиратись із переліку значень, що виключені із списку (не рекомендуються або заборонені). Кортеж параметрів еліптичної кривої має генеруватись випадково. Для цього рекомендується використовувати випадкові бітові рядки SEED. Указане стосується генерації загально - системних параметрів еліптичних кривих над скінченними полями 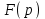 , , 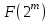 та та 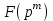 . Вибір способів та засобів генерування SEED має здійснюватись з урахуванням вимог законодавства. . Вибір способів та засобів генерування SEED має здійснюватись з урахуванням вимог законодавства.1.10.4 Перелік, сутність, вимоги та стан стандартизації методів побудування загально - системних параметрів для криптографічного перетворення в фактор - кільці. 1.10.4.1 Основні підходи вимоги до побудування загально - системних параметрів перетворень в фактор - кільці. Загально - системними параметрами алгоритму NTRUEncrypt є кортеж {N, q, p}. Детальний опис такого кортежу наводиться в пункті 1.6.7. Розглянемо вимоги до цього кортежу. Параметр N визначає розмір кільця R - максимальний степінь поліномів кільця, а p і q – два взаємно прості числа. За умови, що малий модуль ділить більший модуль q, то приведення за модулем р виразу p*r*h + m по модулю одразу розкриває значення m. Через це потрібно, щоб більший модуль q та менший модуль p були взаємно простими в кільці Z[X]/(XN-)[217, 177-180. 187]. Тому p і q є модулями, згідно з якими зводяться коефіцієнти поліномів фактор - кілець. Окрім того, параметр р визначає інтервал, якому мають належати всі коефіцієнти поліномів, що використовуються в криптосистемі NTRUEncrypt. Так, простір повідомлень LM визначається як LM = {M(x) 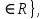 (1.199) (1.199)причому коефіцієнти поліномів-повідомлень належать інтервалу [– (p –1)/2, (p – 1)/2]. (1.200) У стандарті Х9.98 в якості q використовується ступінь числа 2(211= 2048), а p=3. Необхідно, щоб параметр стійкості N був простим числом. Якщо N складається з багатьох (у тому числі й однакових) співмножників (наприклад, якщо N – ступінь двійки), то як показав Гентрі [217], метод згортки (foldingmethod) дозволяє відновити особистий ключ і вихідне повідомлення з решітки розмірністю набагато менше ніж N. Для запобігання атак, заснованих на факторизації h та r, необхідно, щоб для кожного простого дільника Р модуля q порядок P(modN) повинен бути N-1 або (N-1)/2. Ця вимога pf,tpgtxe’ df;kbdbq побічний ефект – зростання ймовірності того, що вибраний випадковим чином особистий ключ f буде оборотнім в R q. Якщо у перетворенні r х h(modq) q буде використане маленьким або не буде існувати f–1 (Z/qZ) [X]/(XN– 1), криптоаналітик може використати знання h для розв’язання e= rh+ m’ з використанням лінійної алгебри та отримати значення повідомлення m. Аналіз показав, що немає відомих проблем стійкості відносно модуля q - він може бути як простим, так і складеним числом. В стандарті Х9.98 q вибрано рівним 2l для деякого l , так як це забезпечує зростання ефективності виконання операцій приведення за даним модулем. Асиметричною парою ключа є кортеж випадкових поліномів (f, fp, h), де (f, fp) – особистий (конфіденційний) ключ отримувача направлено зашифрованого повідомлення, а h – відкритий ключ зашифрування. Одноразовими ключами є багаточлени g та r, де g – поліном, за допомогою якого обчислюється відкритий ключ h, а r – ключ сеансу зашифрування. Також до ключа визначені його параметри числа - df, dg та dr. Ці параметри визначають коефіцієнти множини багаточленів відповідно: Lf = L (df, df – 1); Lg = L(dg, dg); (1.2013) Lr = L(dr, dr). У (1.201), наприклад, запис у вигляді L (df, df – 1) означає, що множина Lf є сукупністю можливих багаточленів кільця R, кожен із яких в якості коефіцієнтів має df одиниць (1) та (df – 1) від’ємних одиниць (–1), а ті коефіцієнти, що залишилися, приймають нульові значення. По аналогії визначається число (1), (-1) та (0) і для Lg та Lr. Значення загальносистемних параметрів згідно стандарту X9.98 наведені у таблиці 1.30. В таблиці кожного рівня безпеки перший рядок – це набір параметрів, оптимізованих за розміром, другий рядок – набір параметрів, оптимізованих за швидкістю, третій рядок - набір параметрів, оптимізованих за загальними затратами (усереднене). Таблиця 1.30. – Загальносистемні параметри згідно X9.98.
Набори параметрів, наведені у даному стандарті для використання з деяким рівнем стійкості k, фактично мають рівень стійкості k' > k проти зловмисника, що використовує найкращі з відомих у липні 2008 року атаки. У таблиці 1є31 порівнюються реальні рівні стійкості наборів параметрів з їх заявленими рівнями стійкості. Таблиця 1.31 – Стійкість рекомендованих наборів параметрів у порівнянні з кращими на сьогоднішній день атаками
1.10.4.2 Методи генерування та вимоги до ключових даних. Генерування ключів. При генеруванні ключів вважаються відомими загальні параметри та параметри ключів. За таких умов генерування ключів здійснюється у певній послідовності. 1. Із повної множини Lf обчислюється особистий (конфіденційний) багаточлен ключ f(x). 2. Із повної множини Lg обчислюється особистий (конфіденційний) багаточлен ключ g(x). 3. За відомим f(x) обчислюються мультиплікативно зворотні в кільці R для нього багаточлени fq(x) та fp(x), які задовольняють умовам: f(x) * fq(x)=1(mod q); f(x) * fp(x)=1(mod p). (1.202) 4. Обчислюється відкритий ключ h(x) = fq(x)* g(x) (modq) (1.203) 5. Як особистий (конфіденційний) ключ вибирається пара (f(x), fp(x)). 6. Відкритий ключ h(x) повинен бути доступним усім користувачам (абонентам) із забезпеченням його цілісності, справжності, доступності й неспростовності. Особистий ключ f і одноразовий поліном g у загальному випадку повинні генеруватись випадковим (псевдовипадковим) чином, але для f повинні існувати зворотні поліноми як за модулем p, так і за модулем q. Наприклад, для стандарту X9.98 він повинен мати наступний вигляд: f = 1 + p*F, (1.204) де F генерується за допомогою примітиву lbp-kgp-3, p — менший модуль, ціле число (у даному стандарті p = 3). Ключі повинні генеруватись або з використанням генератора випадкових бітів RBG у зв’язці з індексною функцією генерації IGF для Х9.98, або за допомогою випадкових чисел (діапазон значень від 0 до N-1). Щоб ключі відповідали рівню безпеки в k біт, генератор випадкових біт повинен бути ініціалізований хоча б 64+k бітами ентропії (тобто виконувати 64+k холостих циклів генерації. Для реалізації алгоритму зашифрування необхідно згенерувати поліном r (ключ сеансу зашифрування). У загальному випадку ключ - поліном r повинен обиратись випадковим (псевдовипадковим) чином (зі ступенем не більшим, ніж N-1). У стандарті Х9.98 він детерміновано формується з повідомлення m та солі b за допомогою примітиву lbp-bpgm-3[217]. При розшифруванні обчислюється поліном a = f * e mod q. (1.204) У стандарті IEEEP 1363.1 для зменшення ймовірності неправильного розшифрування поліном а має коефіцієнти не в діапазоні [0, q-1], а в діапазоні [-q/2, q/2]. У стандарті Х9.98 коефіцієнти полінома а повинні лежати в межах [A, A + q-1], де A – загальносистемний параметр, яки залежить від інших ЗСП, зазвичай велике від’ємне число. Розшифроване повідомлення m* у загальному випадку може не співпадати з вихідним, тому що приводиться як за модулем p, так і за модулем q у вигляді a = r*gp + f*m mod q. Тому необхідно, щоб поліном a мав коефіцієнти з такого інтервалу, щоб їх не потрібно було приводити за модулем q. Це дозволить однозначно відновити вихідне повідомлення. 1.10. 4.3 Порівняльний аналіз методів направленого шифрування за критеріями складності (з точки зору загальносистемних параметрів). Використовуючи дані таблиці 1.32 проведемо аналіз методів направленого шифрування з точки зору загальносистемних параметрів за критеріями складності. У таблиці 1.32 наведені результати порівняння розмірів ключів для NTRU, RSA та еліптичних кривих (EC) [29-21, 217, 238, 378-379, 361-364]. Причому прийнято, що для NTRU та RSA розмір блоку шифротексту порівняний з розміром відкритого ключа. Таблиця 1.32 – Порівняння розмірів ключів для NTRUEncrypt та інших алгоритмів з відкритими ключами
Із таблиці слідує, що довжина відкритого ключа NTRU в декілька разів більша за ключ RSA, а довжина особистого ключа в декілька разів менша. Але на високому рівні стійкості (256 бітів) навіть відкритий ключ NTRU менший або приблизно дорівнює довжині ключа RSA, а особистий ключ NTRU має довжину на порядок меншу. У цілому відносно NTRU Х9.98 можна зробити такі висновки. 1.10.5 Загальні висновки та рекомендації до направленого шифрування в фактор - кільці. 1. Модулі p та q повинні бути були взаємно простими. 2. Інтервал, у якому повинні лежати коефіцієнти поліномів-повідомлень, повинен вибиратись в межах [A, A + q-1]. 3. Параметри N, q, та p повинні мати певні обгунтовані співвідношення. 4. Особливістю NTRU Х9. 98 є те, що тільки розробником визначені та рекомендуються до використання конкретні значення загальносистемних параметрів. Відповідні значення наведено в таблиці 1.31, і тільки при їх використанні розробник гарантує вказані рівні стійкості. 5. У таблиці 1.31 наведена реальна стійкість рекомендованих наборів параметрів у порівнянні з запропонованою відповідно до рівня стійкості. Аналіз їх значень дозволяє зробити висновок, що реальна стійкість дещо перевищує запропоновану; 6. У таблиці 1.32 наведені результати оцінки розмірів ключів для NTRUEncrypt та інших алгоритмів з відкритими ключами, які дозволяють зробити висновки про перевагу крипто перетворень, а також визначити проблемні питання крипто перетворень в кільці зрізаних поліномів. 6. Запропоновані попередні оцінки алгоритму відносно стійкості до основних атак, що можуть бути реалізовані на алгоритм NTRUEncrypt. Також в таблиці 3.4 наведені оцінки часу криптоаналізу відносно основних алгоритмів на відкритих ключах для різних рівнів безпеки. 7. Із стандарту Х9.98 NTRUEncrypt можливо реалізувати ефективний захист від несанкціонованого доступу через застосування простих пристроїв, таких як смарт - карти та електронні ключі. Так за даними компанії NTRU Cryptosystem безконтактні смарт - карти з NTRUEncrypt будуть коштувати у 6-10 раз дешевше за смарт - карти з RSA. 8. Згідно стандарту Х9.98 NTRUEncrypt може використовуватися також для транспортування симетричних ключів із забезпеченням криптографічного захисту. 9. Безпосередньо криптографічні перетворення в фактор - кільці NTRUEncrypt визначені тільки в стандарті Х9.98 NTRUEncrypt. Для їх застосування необхідно відповідним чином здійснити гармонізацію, або розробити з використанням аналогічних або розширених вимог національний стандарт. 10. Одним із недоліків Х9.98 NTRUEncrypt є розширення у порівнянні з іншими алгоритмами направленого шифрування довжини криптограми. Бажано щоби вона була мінімізована. 11. Іншим недоліком Х9.98 NTRUEncrypt є збільшення довжин відкритих L в та особистих ключів асиметричних пар. 1.11 Проблемні питання теорії та практики побудування та аналізу криптосистем та напрями їх вирішення. 1.11.1 Основною метою проведення криптоаналізу необхідно вважати визначення криптографічної стійкості криптографічних перетворень, перш за все у сенсі неможливості чи можливості визначення спеціальних (ключових) даних тощо. Для визначення ступеня небезпечності таких дій можна застосовувати різні підходи. Кращими з них є врахування можливостей зовнішнього порушника (криптоаналітика). Криптоаналіз також має здійснюватись перш за все розробником з метою доведення рівня гарантій щодо криптографічної стійкості систем та засобів КЗІ, що задекларована розробником та очікується замовником, в тому числі в процесі їх застосування та удосконалення. Вважається за необхідне відійти від традиційного розгляду зовнішнього порушника. При дослідженнях пропонується розглядати такі джерела загроз: - іноземних розробників ІТ технологій і систем безпеки, які співпрацюють зі спецслужбами з питань вбудовування несанкціонованих функцій; - національних розробників ІТ технологій та систем безпеки, які переслідують свої комерційні інтереси чи співпрацюють зі спецслужбами; - спеціальні служби та підрозділи технологічно розвинених держав; - внутрішніх (санкціонованих) співробітників та спеціалістів (інсайдерів); - зовнішніх порушників 0 - 3 рівнів згідно [ 212 ]. 1.11.2Важливими проблемами теорії та практики надання електронних довірчих послуг, які повинні бути вирішеними, в першу чергу засобом використання криптографічних перетворень[210, 329, 76, 93] є такі: - уніфікація та стандартизація криптографічних примітивів, криптографічних механізмів та протоколів при наданні електронних довірчих послуг згідно з Регламентом 2012 та Регламентом 2014; - уніфікація, стандартизація та створення систем безпечних електронних послуг з електронної ідентифікації, електронної автентифікації, електронного підпису,електронного штампу, електронної мітки часу, електронних документів, електронної доставки документів та електронної автентифікації веб - сайтів; - вдосконалення та розробка нових методів, механізмів та алгоритмів криптографічних перетворень та криптографічних протоколів; - прогнозування розвитку, стандартизації, уніфікації та вдосконалення криптографічних перетворень та криптографічних протоколів; - практичне створення та впровадження уніфікованих програмно - технічних комплексів та систем для третьої довіреної сторони; - уніфікація технічних специфікацій форматів даних та протоколів взаємодії. 1.11.3 у залежності від умов експлуатації засобів КЗІ та відповідно до цінності інформації, що захищається, необхідно розглядати чотири рівні порушника: Нульовий рівень – випадкове ненавмисне ознайомлення зі змістом інформації (випадкове прослуховування в каналі); Перший рівень – порушник має обмежені кошти та самостійно створює засоби і методи атак на засоби КЗІ, а також інформаційно-телекомунікаційні системи із застосуванням широко розповсюджених програмних засобів та електронно-обчислювальної техніки; Другий рівень – порушник корпоративного типу має змогу створення спеціальних технічних засобів, вартість яких співвідноситься з можливими фінансовими збитками при втраті, спотворенні та знищенні інформації, що захищається. У цьому разі для розподілу обчислень при проведенні атак можуть застосовуватись локальні обчислювальні мережі; Третій рівень – порушник має науково-технічний ресурс, який прирівнюється до науково-технічного ресурсу спеціальної служби економічно розвиненої держави. Основним критерієм при визначенні дій порушника є рівень збитків, який пропонується оцінювати такими категоріями: 1 – незначні, 2 – значні, але здебільшого припустимі, 3 – середні, 4 – дуже значні. При практичній оцінці можна вважати, що порушник першого рівня може вкласти у розв’язання задач криптоаналізу $ (104 – 2 104), другого рівня – $ (106 –107), третього – $ (109 – 2 109). 1.11.4 Загальні завдання забезпечення безпеки в кібер середовищі можуть включати такі основні послуги як: доступність, цілісність, конфіденційність. Можна вважати, що порушення кібербезпека зводиться до здійснення кібер атаки. Кібер атака - дії, що спрямовані на маніпулювання критично важливими системами, ресурсами, інформацією (порушення конфіденційності) або її крадіжку, блокування (порушення доступності), псування (спотворення), руйнування і знищення (порушення цілісності) У проекті Закону України «Про внесення змін до Закону України" Про основи національної безпеки України "Щодо кібернетичної безпеки України» (Номер, дата реєстрації: 2483 від 07.03.2013) міститься таке визначення термінів: "Кібернетична безпека (кібербезпека) - це стан захищеності життєво важливих інтересів людини й громадянина, суспільства та держави в кібер просторі. При цьому кібернетичний простір (кіберпростір) - це середовище, що виникає в результаті функціонування на основі єдиних принципів и за загальними правилами інформаційних, телекомунікаційних та інформаційно-телекомунікаційних систем. Можна зробити висновок про те, що поняття кінетичної безпеки є більш вузьким чим інформаційної безпеки, а останнє може включає перше. 1.11.5 Використання хмарних обчислень не тільки дозволяє реалізувати можливість віддаленої швидкої обробки інформації та забезпечує досягнення високих показників відмово стійкості інформаційної інфраструктури, але й вносить додаткові загрози інформаційній системі та інформації, що там обробляється. Під хмарою можна розуміти спрощене подання сукупності технологій та апаратного забезпечення, що складається із обчислювальних ресурсів, сховищ даних, апаратури віртуалізації, сервера управління запитами і так далі. Клієнтські комп’ютери через мережу зв’язку (наприклад Інтернет) з’єднуються із сервером, який обробляє запроси та керує наступними діями щодо роботи системи хмари та її взаємодією із клієнтом. 1.11.6 Якщо головним для користувача при обчисленнях в хмарах є забезпечення конфіденційності, то найкращим засобом захисту можна назвати криптографічний захист інформації. При використанні систем хмарних обчислень у споживача відсутня можливість застосування додаткових засобів обмеження доступу до інформації , таких як контроль фізичного доступу та інших організаційних і технічних заходів, тобто єдиним надійним контрольованим засобом захисту інформації може стати криптографічний засіб. Основними методами в цьому випадку є використання симетричного та направленого шифрування, цифрових підписів та протоколів захищеного обміну даними. Всі ці механізми та методи можна об’єднати спеціальними системами або програмними компонентами, які в цілому можна назвати механізмом забезпечення захищеного обміну інформацією. До переваг таких механізмів можна віднести наступне: криптографічна безпека встановлюваного з’єднання; відкритість при певних умовах програмного коду, що дає можливість програмістам вдосконалювати протоколи до певного рівня та розробляти додатки до нього; розширюваність, що згодом надасть можливість використовувати нові криптографічні алгоритми, геш-функції та криптографічні протоколи; відносна ефективність, яка обґрунтовується завдяки спеціальній технології зменшення активності робочої машини, що використовується майже у всіх протоколах поданого типу. Таким чином, механізми криптографічного захищеного обміну інформацією є дуже зручним та адекватним рішенням проблеми забезпечення конфіденційного обміну даними при обчисленнях в хмарі. Такі механізми у цілому відповідають головним вимогам до технології безпечного обміну даними. Основними та визначними вимогами з цих вимог є такі: 1) Забезпечення конфіденційності, цілісності та доступності (КЦД), а також при необхідності неспростовності та надійності з відповідними рівнями гарантій на всіх етапах обробки інформації у хмарі. 2) Ефективність роботи механізму безпеки,тобто досягнення забезпечення КЦД засобом витрати адекватної кількості матеріально - технічних ресурсів. 3) Можливість реального впровадження з урахуванням потреб та різного типу забезпечення. 4) Використання сертифікатів для ідентифікації та автентифікації. 5) Застосування електронних довірчих послуг у відповідності з нормативно - правовою базою. 1.11.7 Однією з фундаментальних задач теорії стійкості є класифікація криптографічних систем за рівнем гарантій стійкості. Її можна вирішити на основі використання параметрі кортежу (2.15) - (N k, H(К), 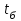 , γ, Ру, l0) , але при цьому, на наш погляд, провідним показником є безпечний час , γ, Ру, l0) , але при цьому, на наш погляд, провідним показником є безпечний час 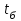 . .У залежності від складності задачі криптоаналізу, криптографічні перетворення (шифри) за криптографічною стійкістю можна поділити на чотири класи: 1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||