Шпоры ЛСАР. 1 1 Основные понятия и определения тау
 Скачать 421.5 Kb.
|
|
10 1) Математическое описание линейных САР. Исследование САР и ееэлементов связаны с изучением процессов в этих САР или ее элементов. Математическая формулировка этих законов определяет уравнение которое может быть положено на основе анализа. Эти ур-я линейные с диф-ми постоянными коэф-ми; лине-е дифер-е с переменными коэф-ми; нелинейные ур-я и алгебраические ур-я. Любая САр состоит изсвязана м/у собой элементамипоэтому диф ур-е можшо получить состовляя уравнения отдельных элементов 2) Критерий устойчивости найквеста Этот критерий является графическим критерием. Правила, с помощью которых можно установить по АФЧХ разомкнутой системы необходимое и достаточное условие замкнутой системы. Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала на действительной оси координат от -1, j0. Второй случай соответствует неустойчивой САР. Эта точка называется критической. Если же АФЧХ проходит через точку (-1; j0), то САР будет находиться на границе устойчивости. Если неустойчивая система имеет в правой полуплоскости петлю, то эта система будет устойчива в замкнутом состоянии и если АФЧХ разомкнутой системы описываемая концом вектора 1+W, при возрастании частоты от нуля до ∞ стрелка вектора обойдет критическую точку против часовой стрелки k раз. Это является необходимым и достаточным условием. 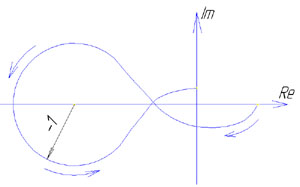 11 1. Математическое описание линейных САР. Исследование САР и ее элементов связаны с изучением процессов в этих САР или ее элементов. Математическая формулировка этих законов определяет уравнение которое может быть положено на основе анализа. Эти ур-я линейные с диф-ми постоянными коэф-ми; лине-е дифер-е с переменными коэф-ми; нелинейные ур-я и алгебраические ур-я. Любая САр состоит изсвязана м/у собой элементамипоэтому диф ур-е можшо получить состовляя уравнения отдельных элементов 2) Анализ устойчивости по логарифмическим характеристикам. Если ЛАХ разомкнутой САР пересекает ось частоты ранее чем ЛФХ пересекает ось (-180) то замкнутая САР будет устойчива. 12 1) Передаточная функция звена. 2) Устойчивость линейных систем. Критерий устойчивости Найквиста. Устойчивость линейных систем В процессе работы на систему действуют различные возмущающие силы, вызывающие ее отклонение от заданного закона движения. Если под влиянием возмущения система отклонилась от состояния равновесия и после прекращения действия внешнего возмущения снова вернулась в исходное состояние, то такая система устойчива. Если под влиянием внешнего возмущения система будет отклоняться от состояния равновесия, а после прекращения действия возмущения система не возвращается в исходное состояние, а удаление системы с течением времени возрастает, то такая система называется неустойчивой. В линейных системах отклонение при неустойчивом движении будет неограниченно возрастать. Необходимое и достаточное условие устойчивости является выполнение требования, в соответствии с которым характеристическое уравнение системы должно иметь отрицательную вещественную часть. Наличие среди корней характеристического уравнения хотя бы одного корня с положительной вещественной частью свидетельствует о невыполнении этого условия, т.е. приводит к неустойчивости системы. Устойчивость в линейной системе характеризуется затуханием переходного процесса. Т.к. затухание переходного процесса в свою очередь определяется только корнем характеристического уравнения и не зависит от воздействия, то устойчивость является внутренним свойством линейной системы. Для определения устойчивости системы необходимому и достаточному условию нужно уметь находить корни характеристического уравнения. Это можно сделать просто для уравнения 1-го и 2-го порядков. Реальные системы десятых, сотых порядков. Поэтому для анализа устойчивости без нахождения корней характеристического уравнения, используют критерии устойчивости. Критерий устойчивости найквеста Этот критерий является графическим критерием. Правила, с помощью которых можно установить по АФЧХ разомкнутой системы необходимое и достаточное условие замкнутой системы. Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала на действительной оси координат от -1, j0. Второй случай соответствует неустойчивой САР. Эта точка называется критической. Если же АФЧХ проходит через точку (-1; j0), то САР будет находиться на границе устойчивости. Если неустойчивая система имеет в правой полуплоскости петлю, то эта система будет устойчива в замкнутом состоянии и если АФЧХ разомкнутой системы описываемая концом вектора 1+W, при возрастании частоты от нуля до ∞ стрелка вектора обойдет критическую точку против часовой стрелки k раз. Это является необходимым и достаточным условием. 13 1. Передаточная функция системы, соединенных между собой звеньев. Передаточная функция системы – отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых нач. условиях. Ф(s)=X(s)/G(s), s=p – показатель дифференцирования  2. Устойчивость линейных систем. Критерий устойчивости Раусса-Гурвица. Устойчивость линейных систем В процессе работы на систему действуют различные возмущающие силы, вызывающие ее отклонение от заданного закона движения. Если под влиянием возмущения система отклонилась от состояния равновесия и после прекращения действия внешнего возмущения снова вернулась в исходное состояние, то такая система устойчива. Если под влиянием внешнего возмущения система будет отклоняться от состояния равновесия, а после прекращения действия возмущения система не возвращается в исходное состояние, а удаление системы с течением времени возрастает, то такая система называется неустойчивой. В линейных системах отклонение при неустойчивом движении будет неограниченно возрастать. Необходимое и достаточное условие устойчивости является выполнение требования, в соответствии с которым характеристическое уравнение системы должно иметь отрицательную вещественную часть. Наличие среди корней характеристического уравнения хотя бы одного корня с положительной вещественной частью свидетельствует о невыполнении этого условия, т.е. приводит к неустойчивости системы. Устойчивость в линейной системе характеризуется затуханием переходного процесса. Т.к. затухание переходного процесса в свою очередь определяется только корнем характеристического уравнения и не зависит от воздействия, то устойчивость является внутренним свойством линейной системы. Для определения устойчивости системы необходимому и достаточному условию нужно уметь находить корни характеристического уравнения. Это можно сделать просто для уравнения 1-го и 2-го порядков. Реальные системы десятых, сотых порядков. Поэтому для анализа устойчивости без нахождения корней характеристического уравнения, используют критерии устойчивости. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВЕЦА Необходимым и достаточным условием устойчивости системы любого порядка без решения характеристического уравнения, по рассмотрению его коэффициентов, были сформулированы учеными Раусом и Гурвицом. Руас сказал, что для выполнения условия устойчивости, а следовательно для расположения всех корней характеристического уравнения в левой полуплоскости , необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.   Гурвец дополнил, что для выполнения условия устойчивости, а следовательно, для расположения вех корней характеристического уравнения в левой полуплоскости, необходимо и достаточно, чтобы все n диагональных миноров матрицы были положительны. 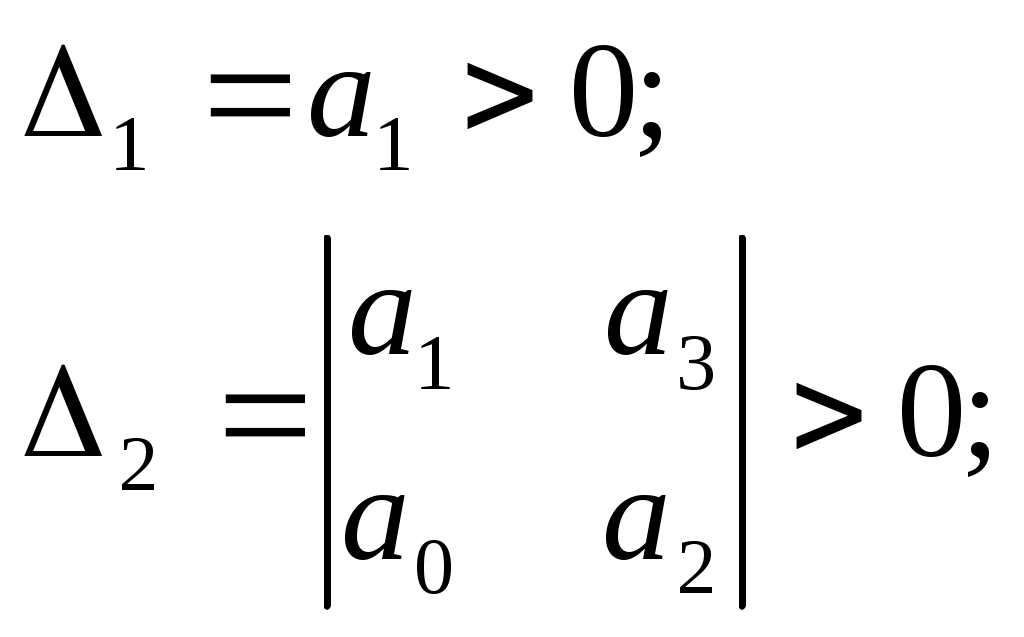 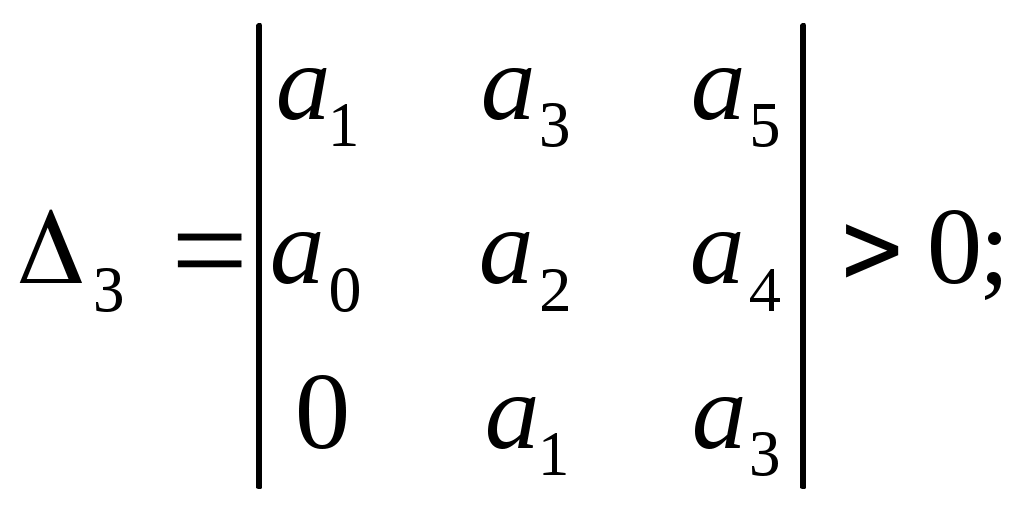 Критерий устойчивости Рауса и Гурвеца является алгебраическим, т.к. при их использовании задача определения знаков вещественных частей хар. уравнения сводится к выполнению общих алгебраических операций. 14 1) Структурные схемы и их преобразование. Последовательное соединение звеньев. Структурная схема САУ в простейшем случае строится из элементарных динамических звеньев. Но несколько элементарных звеньев могут быть заменены одним звеном со сложной передаточной функцией. Для этого существуют правила эквивалентного преобразования структурных схем. Рассмотрим возможные способы преобразований.  Последовательное соединение (рис.28) - выходная величина предшествующего звена подается на вход последующего. При этом можно записать: y1 = W1  yo; y2 = W2 y1; ...; yn = Wn yn - 1 = > yn = W1 W2.....Wn.yo = Wэкв yo, где  . То есть цепочка последовательно соединенных звеньев преобразуется в эквивалентное звено с передаточной функцией, равной произведению передаточных функций отдельных звеньев. 2) Построение логарифмических характеристик последовательно соединенных типовых динамических звеньев Пусть передаточная функция части системы 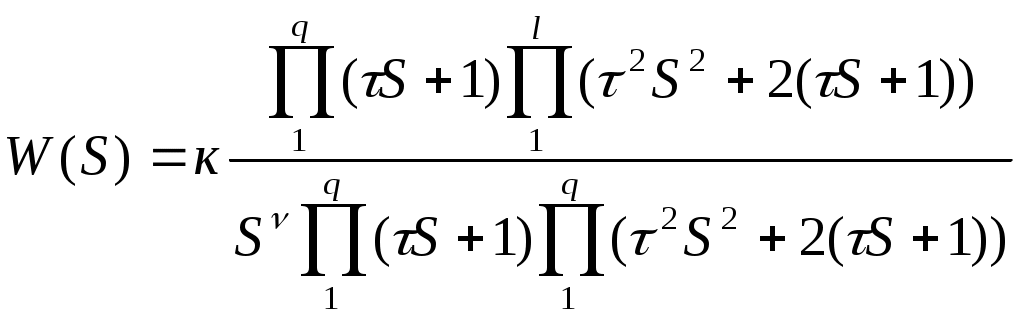 Подставив вместо S jω найдем модуль, затем логарифмируя, найдем выражение 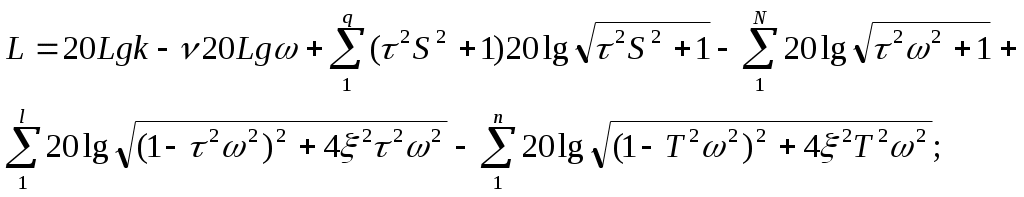 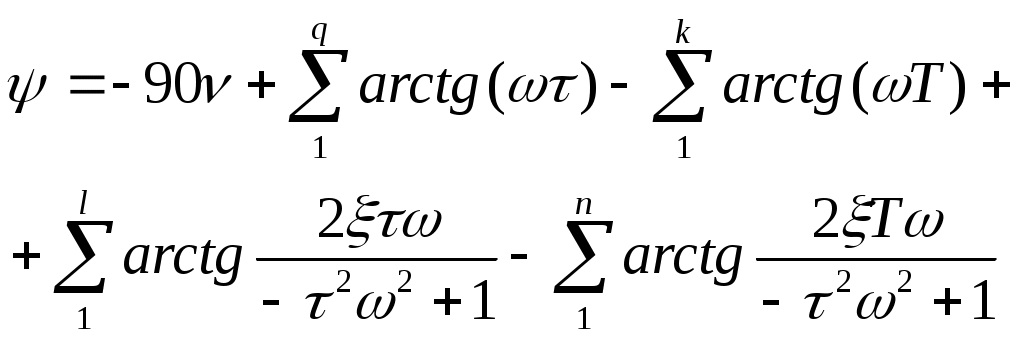 Эти формулы показывают, что результирующие характеристики определяются суммой логарифмических и фазовых характеристик типовых звеньев. 15 1) 2. Параллельно - согласное соединение (рис.29) - на вход каждого з 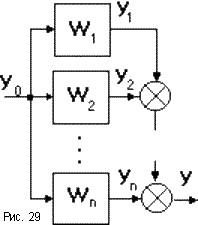 вена подается один и тот же сигнал, а выходные сигналы складываются. Тогда:y = y1 + y2 + ... + yn = (W1 + W2 + ... + W3)yo = Wэкв yo, где  . То есть цепочка звеньев, соединенных параллельно - согласно, преобразуется в звено с передаточной функцией, равной сумме передаточных функций отдельных звеньев. 16, 17, 18 19 1)Характеристики динамических звеньев. Частотные характеристики Частотные характеристики Рассмотрим передаточную функцию, состоящую из n-го количества элементов. Последовательность выражений позволяет найти амплитуду и фазу колебаний на выходе системы при гармоническом воздействии на ее входе. Модуль этого выражения показывает, во сколько раз увеличивается или уменьшается амплитуда колебаний на выходе системы по сравнению с амплитудой колебаний на входе. Аргумент вектора F(jω) описывает фазовый угол колебаний по отношению колебаниям на входе => (*) определяет частотную характеристику, называемую амплитудно-фазовой частотной характеристикой (АФЧХ). АФЧХ строится на комплексной плоскости  j – мнимая единица.  - коэффициент, характеризующий изменение амплитуды при изменении частоты, при изменяющейся частоте, называется амплитудно-частотной характеристикой (АЧХ). дает представление о фазовом сдвиге выходных колебаний и он называется фазово-частотной характеристикой (ФЧХ)Вещественные или мнимые частотные характеристики связаны с АЧХ и ФЧХ следующим образом: 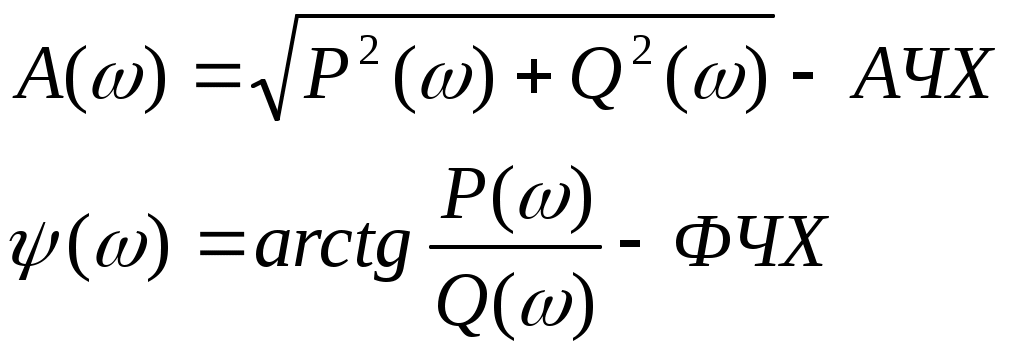 При анализе САР на устойчивость и качества процесса регулирования, а также при решении других задач, часто обращаются к ЛЧХ Усиление L(ω) = 20lg|Ф(jω)| = 20lgA(ω) [дБ] – является единицей логарифмической относительно величины. Изменения относительно двух величин в 10 раз соответствует изменению усиления на 20 дБ. Известно, что АЧХ представляет собой отношение 2-х амплитуд: входного и выходного сигналов. 20 1)Характеристики динамических звеньев. Прееходная функция системы Переходная функция системы Переходной функцией САР называется переходный процесс системы, вызванный единичным ступенчатым воздействием при нулевых начальных условиях. Используя понятие передаточной функции замкнутой системы и обратное преобразование Лапласа можно для переходной функции системы записать выражение:  . Если изображение управляющего сигнала G(S) является изображением единичного ступеньчатого воздействия, то его можно представить как  , тогда выражение будет определять переходную функцию в следующем виде:  - эта формула характеризует реакцию системы при единичном скачке и является переходной функцией.21 1) В примене к нелинейности состоит Пусть передаточная функция замкнутой системы будет представлена W(S)=K(S)/D(S) в этом случае диф уравнение замкнутой нелинейной САР можно представить D(S)X(S)+K(S)D(X)=0 Пусть функция f(x) однозначная функция, заменяем ее суммой линейной функции не линейных слагаемых: f(x)=c(x)+µφ(x) выбираем с таким чтобы уравнение при µ=0 имело следующий вид [D(S)+CK(S)]X=0 Решение этого уравнения имело бы чисто мнимые корни, вот такая линеаризация называется эквивалентной 2) Структурная схема САУ в простейшем случае строится из элементарных динамических звеньев. Но несколько элементарных звеньев могут быть заменены одним звеном со сложной передаточной функцией. Для этого существуют правила эквивалентного преобразования структурных схем. Рассмотрим возможные способы преобразований. 1. Последовательное соединение (рис.28) - выходная величина предшествующего звена подается на вход последующего. При этом можно записать: y1 = W1 yo; y2 = W2 y1; ...; yn = Wn yn - 1 = > yn = W1 W2.....Wn.yo = Wэкв yo, где . То есть цепочка последовательно соединенных звеньев преобразуется в эквивалентное звено с передаточной функцией, равной произведению передаточных функций отдельных звеньев. |