Шпоры ЛСАР. 1 1 Основные понятия и определения тау

• Название: 1 1 Основные понятия и определения тау
• Дата: 20.04.2023
• Размер: 421.5 Kb.
• Имя файла: Шпоры ЛСАР.doc
• Тип: Закон; #1075820
• страница: 3 из 3

22

1) Построение логарифмических характеристик последовательно соединенных типовых динамических звеньев

Пусть передаточная функция части системы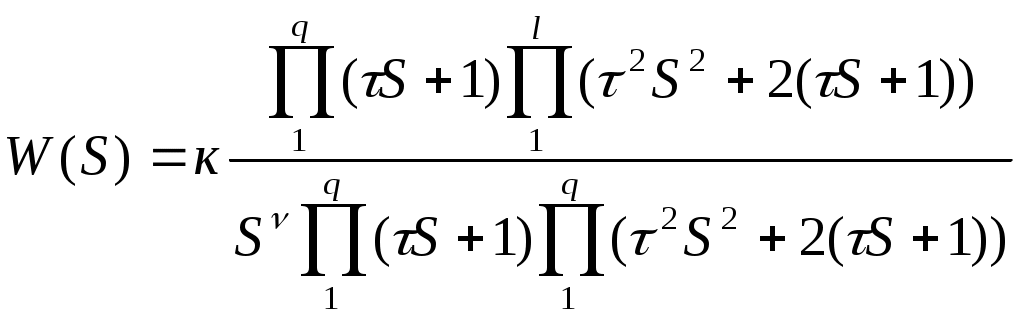

Подставив вместо S jω найдем модуль, затем логарифмируя, найдем выражение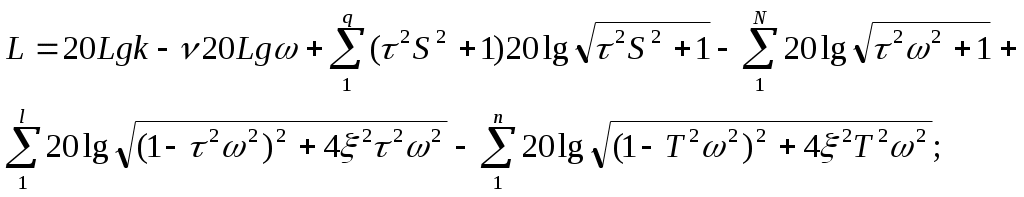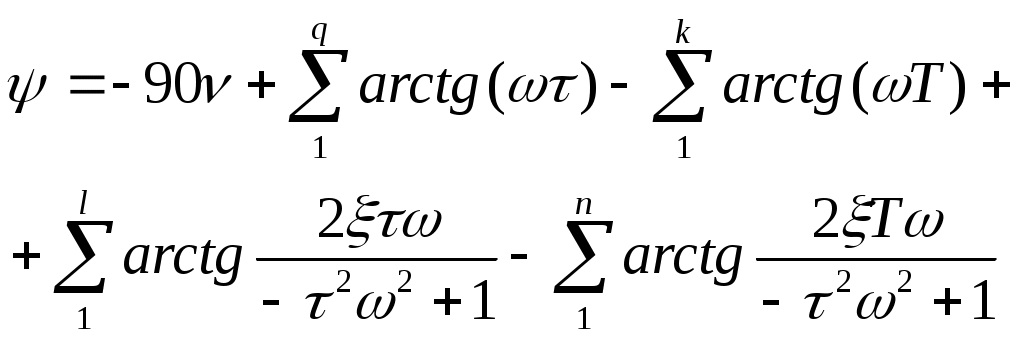

Эти формулы показывают, что результирующие характеристики определяются суммой логарифмических и фазовых характеристик типовых звеньев.

2)ЛЕКЦИИ


23

1) Основные показатели качества системы

Правильно спроектированная САР должна отвечать указанной точности и плавности протекания процесса, под влиянием управляющего или возмущающего воздействия.



Пусть эта система находится в состоянии переходного процесса. На вход подаем единичное возмущение (g(t) = 1(t)); управляющий сигнал на выходе , где x_св(t) – свободная составляющая переходного процесса, которая обуславливается свойствами системы и соответствующему общему решению другой системы. Х_вын(t) – вынужденная составляющая переходного процесса, обусловленная законом изменения входного воздействия g(t).

Известно, что Х_вын(t) определяет точность САР, а x_св(t) влияет на показатели переходного процесса

Показатели качества процесса регулирования:

1) Перерегулирование – это отношение разности σ = (_Xmax – X_уст)/ X_усn*100% перерегулирование характеризует колебания системы. Допустимый предел (25…30)%

2) Время регулирования характеризует быстроту уравновешивания системы. t_рег принимаем за момент окончания переходного процесса.(допускается отклонение ±5%)

3) Число колебаний регулируемой величины в течении времени переходного процесса. t_{регулир} характеризует колебания системы. (допускается не более 3-х полных колебаний).
24

1)Характеристики динамических звеньев Частотные характеристики

Рассмотрим передаточную функцию, состоящую из n-го количества элементов.

Последовательность выражений позволяет найти амплитуду и фазу колебаний на выходе системы при гармоническом воздействии на ее входе.

Модуль этого выражения показывает, во сколько раз увеличивается или уменьшается амплитуда колебаний на выходе системы по сравнению с амплитудой колебаний на входе.

Аргумент вектора F(jω) описывает фазовый угол колебаний по отношению колебаниям на входе => (*) определяет частотную характеристику, называемую амплитудно-фазовой частотной характеристикой (АФЧХ).

АФЧХ строится на комплексной плоскости j – мнимая единица.

- коэффициент, характеризующий изменение амплитуды при изменении частоты, при изменяющейся частоте, называется амплитудно-частотной характеристикой (АЧХ).

дает представление о фазовом сдвиге выходных колебаний и он называется фазово-частотной характеристикой (ФЧХ)

АФЧХ:

Вещественные или мнимые частотные характеристики связаны с АЧХ и ФЧХ следующим образом: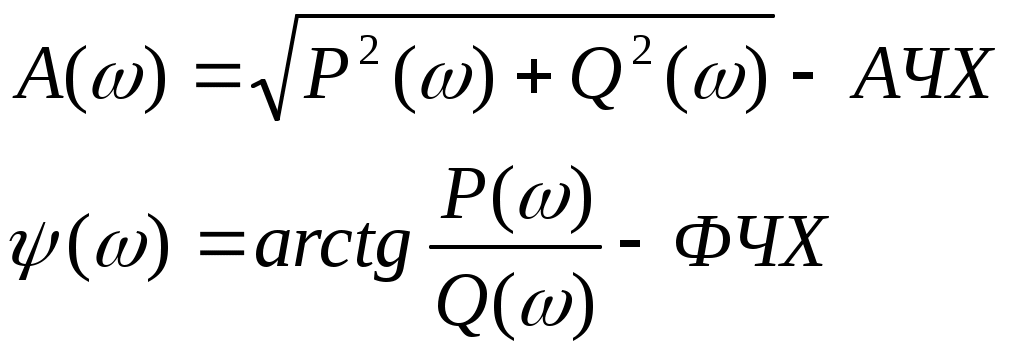



При анализе САР на устойчивость и качества процесса регулирования, а также при решении других задач, часто обращаются к ЛЧХ

Усиление L(ω) = 20lg|Ф(jω)| = 20lgA(ω) [дБ] – является единицей логарифмической относительно величины. Изменения относительно двух величин в 10 раз соответствует изменению усиления на 20 дБ.

Известно, что АЧХ представляет собой отношение 2-х амплитуд: входного и выходного сигналов.
25

2) Статическое и астатическое САР.

Системы стабилизации, программного управления и следящие системы можно разделить на 2 группы:

1 – статические;

2 - астатические;

1) 2)


САР будет статической по отношению к возмущающему или управляющему воздействиям, постоянной величине, отклонению регулируемой величины.

САР явл-ся астатической по возмущению и управляющему воздействию, если при стремлении возмущающего управ. воздействия постоянной величины отклонения регулируемая величина стремится к нулю и не зависит от величины приложенного воздействия. Одна и та же САР может быть астатической по управлению и статической по возмущению, либо наоборот.
26

1. Нелинейной системой автоматического управления наз-ся такая система которая содержит хотябы одно звено описываемое нелинейным уравнением.

В применении к нелинейности состоит

Пусть передаточная функция замкнутой системы будет представлена W(S)=K(S)/D(S) в этом случае диф уравнение замкнутой нелинейной САР можно представить D(S)X(S)+K(S)D(X)=0

Пусть функция f(x) однозначная функция, заменяем ее суммой линейной функции не линейных слагаемых: f(x)=c(x)+µφ(x) выбираем с таким чтобы уравнение при µ=0 имело следующий вид [D(S)+CK(S)]X=0

Решение этого уравнения имело бы чисто мнимые корни, вот такая линеаризация называется эквивалентной.
2. Построение желаемой ЛАХ. Ж. ЛАХ опред. показ. кач. и точн. проц. регулир. Низночастот. ее часть обусл. точн. воспро. медл. измен. возд. По ней можно опред. добротность по скорости и добротность по ускорению, а также статич. ошибку. Частота среза системы опред. с помощью номограмм Солодникова. По перерегулированию опред. вещ. чать САР, а по вещ. части наход. время регулир.: tрег.=kπ/ωсреза, k-коэф. Найдя tрег. можно опред. частоту среза ωсреза. Для наиб. простой реализ. послед. корректир. устройства изломн. накл. жел. ЛАХ (низкочатс.) и ЛАХ желаем. части совпад.

ε(t)=ω3/Dω+ ε3/Dε, ωk=Dω, ωl=Dε^0.5, ω=1/T, tрег.=4,2π/ωсреза, Wустр.=Wжел.-Wнеизм.

27

1) Синтез САР

Сущность задачи синтеза законов состоит в следующем:

Такой выбор структурной схемы САР, а также ее параметров, ее конструктивное решение, при которой обеспечивается требуемые показатели качества и точности процесса регулирования, а сама САР состоит из наиболее простых устройств управления.

Вс. САР можно разделить на:

- объект регулирования (исполнительное устройство, усилитель мощности и измерительные устройства) Все это неизменная часть САР

- корректирующие устройства и усилители – это изменяемая часть

В значительной степени определяющей при выборе устройств неизменяемой части является стоимость, надежность, масса и габаритные размеры.

Порядок синтеза:

• 
  составляется упрощенная структурная схема , выбирается место и схема, включающая корректор и усилители устройств
  
• 
  по критерию качества или требованию показателей качества и точности регулирования подбирают желаемую логарифмическую частотную характеристику разомкнутой САР
  
• 
  Определяют тип и параметры корректирующих устройств САР и составляют окончательную схему САР
  
• 
  Определяют динамические характеристики системы и сравнивают их с соответствующими данными технических условий
  
• 
  Приведенный порядок синтеза может привести к неоднозначности решения задачи.
  

2) Устойчивость импульсных систем

Необходимо и длстаточно что бы полюсы ее передаточной функции распологались в левой полуплоскости комплексной переменной S. Таким образом импульсная система устойчива если, все корни ее характерестического уравнения лежат внутри круга единичного радиуса.

КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВЕЦА

Необходимым и достаточным условием устойчивости системы любого порядка без решения характеристического уравнения, по рассмотрению его коэффициентов, были сформулированы учеными Раусом и Гурвицом.

Руас сказал, что для выполнения условия устойчивости, а следовательно для расположения всех корней характеристического уравнения в левой полуплоскости , необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.

Гурвец дополнил, что для выполнения условия устойчивости, а следовательно, для расположения вех корней характеристического уравнения в левой полуплоскости, необходимо и достаточно, чтобы все n диагональных миноров матрицы были положительны.

Критерий устойчивости Рауса и Гурвеца является алгебраическим, т.к. при их использовании задача определения знаков вещественных частей хар. уравнения сводится к выполнению общих алгебраических операций.

Принадлежность корней к кругу еденичного радиуса может быть установлена при помощи критерия Шур- Кона. До некоторой степени он анологичен критерию Гурвица, однако при его использование необходимо состовлять и анализировать определитель вплоть до до определителя порядка 2п*2п, где п порядок характеристического уравнения.

28

1) Критерий устойчивости найквеста

Этот критерий является графическим критерием. Правила, с помощью которых можно установить по АФЧХ разомкнутой системы необходимое и достаточное условие замкнутой системы. Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала на действительной оси координат от -1, j0. Второй случай соответствует неустойчивой САР. Эта точка называется критической. Если же АФЧХ проходит через точку (-1; j0), то САР будет находиться на границе устойчивости.

Если неустойчивая система имеет в правой полуплоскости петлю, то эта система будет устойчива в замкнутом состоянии и если АФЧХ разомкнутой системы описываемая концом вектора 1+W, при возрастании частоты от нуля до ∞ стрелка вектора обойдет критическую точку против часовой стрелки k раз. Это является необходимым и достаточным условием.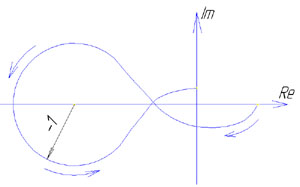



29

1)Изменение неизменной величины во времени определяет переходный процесс и представляет собой динамическую характеристику по которой можно судить о качестве работы системы. Чтобы качественно выполнять задачу регулирования в различных условиях система должна обладать определенным запасом устойчивостим
2)

Устойчивость линейных систем

В процессе работы на систему действуют различные возмущающие силы, вызывающие ее отклонение от заданного закона движения. Если под влиянием возмущения система отклонилась от состояния равновесия и после прекращения действия внешнего возмущения снова вернулась в исходное состояние, то такая система устойчива.

Если под влиянием внешнего возмущения система будет отклоняться от состояния равновесия, а после прекращения действия возмущения система не возвращается в исходное состояние, а удаление системы с течением времени возрастает, то такая система называется неустойчивой.

В линейных системах отклонение при неустойчивом движении будет неограниченно возрастать.

Необходимое и достаточное условие устойчивости является выполнение требования, в соответствии с которым характеристическое уравнение системы должно иметь отрицательную вещественную часть. Наличие среди корней характеристического уравнения хотя бы одного корня с положительной вещественной частью свидетельствует о невыполнении этого условия, т.е. приводит к неустойчивости системы.

Устойчивость в линейной системе характеризуется затуханием переходного процесса. Т.к. затухание переходного процесса в свою очередь определяется только корнем характеристического уравнения

и не зависит от воздействия, то устойчивость является внутренним свойством линейной системы.

Для определения устойчивости системы необходимому и достаточному условию нужно уметь находить корни характеристического уравнения. Это можно сделать просто для уравнения 1-го и 2-го порядков. Реальные системы десятых, сотых порядков. Поэтому для анализа устойчивости без нахождения корней характеристического уравнения, используют критерии устойчивости.
КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВЕЦА

Необходимым и достаточным условием устойчивости системы любого порядка без решения характеристического уравнения, по рассмотрению его коэффициентов, были сформулированы учеными Раусом и Гурвицом.

Руас сказал, что для выполнения условия устойчивости, а следовательно для расположения всех корней характеристического уравнения в левой полуплоскости , необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.

Гурвец дополнил, что для выполнения условия устойчивости, а следовательно, для расположения вех корней характеристического уравнения в левой полуплоскости, необходимо и достаточно, чтобы все n диагональных миноров матрицы были положительны.

Критерий устойчивости Рауса и Гурвеца является алгебраическим, т.к. при их использовании задача определения знаков вещественных частей хар. уравнения сводится к выполнению общих алгебраических операций.
30

1) Статическое и астатическое регулирование.

Системы стабилизации, программного управления и следящие системы можно разделить на 2 группы:

1 – статические;

2 - астатические;

1) 2)


САР будет статической по отношению к возмущающему или управляющему воздействиям, постоянной величине, отклонению регулируемой величины.

САР явл-ся астатической по возмущению и управляющему воздействию, если при стремлении возмущающего управ. воздействия постоянной величины отклонения регулируемая величина стремится к нулю и не зависит от величины приложенного воздействия. Одна и та же САР может быть астатической по управлению и статической по возмущению, либо наоборот
2) Показатели качества процесса регулирования:

1) Перерегулирование – это отношение разности σ = (_Xmax – X_уст)/ X_усn*100% перерегулирование характеризует колебания системы. Допустимый предел (25…30)%

2) Время регулирования характеризует быстроту уравновешивания системы. t_рег принимаем за момент окончания переходного процесса.(допускается отклонение ±5%)

3) Число колебаний регулируемой величины в течении времени переходного процесса. t_{регулир} характеризует колебания системы. (допускается не более 3-х полных колебаний)

1) Собственная частота колебаний системы , где Т_к – период собственных колебаний системы.

2) Логарифмический декремент затухания Характеризует быстродействие системы, т.е., быстроту затухания колебательного процесса.

3) Максимальная скорость сигнала на входе . Данный показатель характеризует быстродействие системы.

Для замкнутой САР, имеющий колебательный переходный процесс, на основе указанных показателей качества можно установить область допустимых отклонений регулируемой величины.

31

2) Устойчивость импульсных систем

Необходимо и длстаточно что бы полюсы ее передаточной функции распологались в левой полуплоскости комплексной переменной S. Таким образом импульсная система устойчива если, все корни ее характерестического уравнения лежат внутри круга единичного радиуса.

КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВЕЦА

W*(s)=H*(s)/G*(s).

Для уст. замкн. имп. системы необх., чтобы z=e^q=(η+1)/(η-1). Полином G*(s)=a0+(a1)e^q+…+(an)e^(nq) в этом случ. можно преобраз. так, чтобы он отображ. внутри единич. круга в пл. z на лев. полупл. η. Поэтому усл. |z|<1 будет соотв. усл., что действ. Re(η)<0.
32

1) Классификация САУ. Следящие системы

САУ в зависимости от характера управляющего воздействия делится на 3 класса:

• 
  система стабилизации;
  
• 
  система программного регулирования;
  
• 
  следящая система;
  

. Следящая система

Управляющее воздействие явл-ся величиной переменной, матем. Описание его во времени не может быть установлено, т.е. неизвестен источник сигнала. Т.к. следящая система предназначена для воспроизведения на выходе управляющего воздействия с возможно большей точностью, то ошибка явл-ся характерной, по которой можно судить о динамических св-вах следящих систем.

Ошибка в следящей системе – это сигнал, в зависимости от величины которого осуществляется управление исполнительного устройства объекта.

2)Типовые нелинейные звенья

1.звено релейного типа

2. звено с кусочно-лминейной характеристикой

3. звено с криволинейной характеристикой

4. звено уравнение которого содержит произведение переменных или их производных и другие их комбинации

5. неленейный импульсный элемент

6. логическое звено

7. звенья описываемые кусочно-линейными диф-ми уравнениями, в том числе переменной структуры.