Шпоры ЛСАР. 1 1 Основные понятия и определения тау

• Название: 1 1 Основные понятия и определения тау
• Дата: 20.04.2023
• Размер: 421.5 Kb.
• Имя файла: Шпоры ЛСАР.doc
• Тип: Закон; #1075820
• страница: 1 из 3

1
1) Основные понятия и определения ТАУ

ТАУ - это научная дисциплина, образующая в совокупности науку об управлении. ТАУ появилась с появлением механизмов.

Линейные непрерывные системы АУ.

Основные понятия АУ:

• 
  рабочая операция;
  
• 
  операция управления;
  

К рабочим операциям отн-ся все действия, необходимые для выполнения процесса в соответствии теми или иными законами, которыми определяется ход данного процесса (вращение вала эл./двигателя). Для улучшения и усовершенствования рабочих операций используются автоматические устройства, которые полностью или частично заменяют труд человека. Замена труда человека наз-ся механизацией.

Для правильного и качественного выполнения операций необходима операция управления. По средствам операции упр-ния обеспечивается в нужный момент времени начало, порядок следования и окончание операции, при этом придаются необх-е параметры самому процессу. Совокупность управления операций образует процесс управления. Операция управления также как и раб. операция частично или полностью выполняться технологическими устройствами в системе. Замена труда человека в операции упр-ния наз-ся автоматизацией. Совокупность средств упр-ния и объекта образует систему управления.

Система, в которой все рабочие и управляющие операции выполняются полностью без участия человека, наз-ся автоматической системой. Система, которая автоматизирует только часть управления, наз-ся автоматизированной системой.

Чтобы осуществить авт. упр-ние или создавать систему упр-ния необходимы конкретные знания рабочего процесса, принципа его работы; необходимы знания методов упр-ния, которые явл-ся общими для самых разнообразных процессов.

При автоматизации упр-ния тех. процессов возникает необходимость в различных группах операций упр-ния. В ТАУ изучают операции по поддержанию заданного закона изменения значений координат.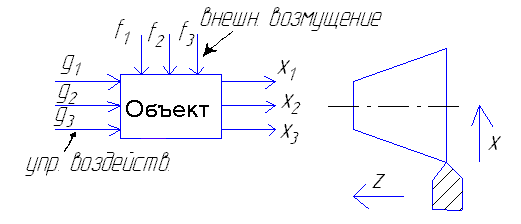



Переменные x, g и f в зависимости от природы объекта могут быть связаны различными соотношениями.

В общем виде: x = A (g,f), где функция А явл-ся оператором объекта определенных видов математической зависимости. Всякий объект обладает массой, т.е. он динамический. Переменные x, g и f динам-х объектов обычно связаны м/у собой дифференциальными, интегральными или разностными уравнениями. В качестве независимой этих переменных выступает время
2. Передаточные функции импульсных систем.

Когда сигнал имп. элем. сущ.: W*(q;0)=Y*(q;0)/(Ku·X*(q;0)). Когда попад. в промеж. между имп.: W*(q;ε)=Y*(q;ε)/(Ku·X*(q;0)). Перед. функции получены из реакции лин. части на послед. имп. Свойства: 1) перед. ф. имп. САР явл. ф. аргум. e^q, т.к. e^q=e^(q+2πi), где i=0;±1; ±2;…. В этом слу. W*(q) явл. периодич. ф. с периодом 2π. 2) перед. ф. W*(q; ε) имеет бесчисл. множ. реш., соотв. различ. знач. парам. ε. 3) Для имп. с паузами знач. передат. ф. для интервалов действ. отлич. от знач. для их пауз.

2.

1) Цель курса состоит в изучении принципов автоматического управления, типов систем автоматического управления, используемых в технике, математического аппарата исследования линейных САУ, основных элементов и характеристик САУ, методов анализа САУ на устойчивость и качество управления, способов корректировки свойств линейных САУ

2. В дискрет. САР контр управл. замык. только на опред. промеж. времени, осущ. возд. на исп. орган импульса. В паузах мажду имп. цепь упр. ост. разомкн. Многие из таких систем сост. из одного исм. элем. и непрер. лин. части. По спос. квантования все имп. САР можно разд.: по врем. квантования – имп. САР; по уровню квантов. – релейн.; по врем. – цифровые.

Импульсная модуляция с помощью имп. элемента.

Имп. элемент преобразует непрерывный сигнал в виде последовательности импульсов. Преобразование непрерывного сигнала в импульсный наз-ся квантованием. Различают след. Виды квантования:

• 
  амплитудно-импульсное (АИМ);
  
• 
  широтно-импульсное (ШИМ);
  
• 
  частотно- импульсное (ЧИМ);
  

1). АИМ – это значит, что амплитуда имп. сигнала зависит от амплитуды непрерывного сигнала в момент квантования. Т-период квантования;  - продолжительность времени.



2). ШИМ  амплитуда импульса явл-ся величиной постоянной. Импульс, как и в варианте АИМ, также повторяется через постоянный промежуток времени. А время действия импульса явл-ся величиной переменной и зависит от амплитуды непрерывного сигнала в момент квантования.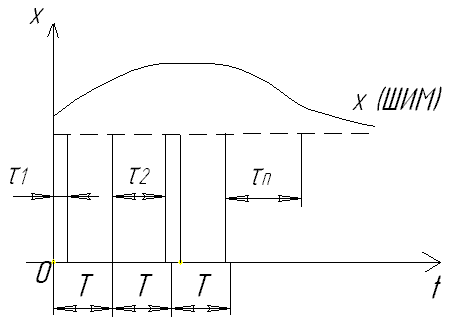



3). ЧИМ. При ЧИМ амплитуда импульса и ширина импульса есть величины постоянные. А частота (период повторяется) импульса зависит от величины амплитуды непрерывного сигнала в момент квантования.



3.

1) Основные принципы регулирования. Принцип разомкнутого управления

В основе алгоритма упр-ния заложены 3 фундаментальных принципа:

1) Принцип разомкнутого управления;

2) Принцип обратной связи;

3) Принцип компенсации (регулирование по возмущению);
1) Принцип разомкнутого управления:



Алгоритм упр-ния строится только на основе алгоритма функционирования и не контролируется по фактическому значению управляемой величины х.

Близость x к U обеспечивается жесткостью характеристик систем. При наличии воздействия f величины х может заметно отклониться от заданной, при этом алгоритм управления станет непригодным.
2) Нелинейные САР. Устойчивость периодических решений

Нелинейной системой автоматического управления наз-ся такая система которая содержит хотя бы одно звено описываемое нелинейным уравнением.

Пусть постр. две кривых. Будем двиг. по Gнэ(A) в напр. возр. ампл. A. Если разомкн. лин. САР уст., то в вход. точке пересеч. этих двух кривых соотв. неуст. периодия. реш. А точке выч. из контура соотв. уст. решений. Для однознач. хар. этот критерий явл. необход., но не достат.



4

1) Основные принципы регулирования. Принцип обратной связи

В основе алгоритма упр-ния заложены 3 фундаментальных принципа:

1) Принцип разомкнутого управления;

2) Принцип обратной связи;

3) Принцип компенсации (регулирование по возмущению);

2) Принцип обратной связи:



 = g – x.

В принципе обратной связи производится управление функции отклонения .

g явл-ся функцией от х : g=F(x).

2) Регулирование по возмущению и комбинированное регулирование

1) Принцип разомкнутого управления:



Алгоритм упр-ния строится только на основе алгоритма функционирования и не контролируется по фактическому значению управляемой величины х.

Близость x к U обеспечивается жесткостью характеристик систем. При наличии воздействия f величины х может заметно отклониться от заданной, при этом алгоритм управления станет непригодным.

3) Принцип компенсации (регулирование по возмущению):



_f = F(g,f)

g = F₁(f) _f = 0 – в установившемся режиме по принципу компенсации (отклонение должно отсутствовать)

При сравнении системы регулирования по возмущению с системой управления, то 1-ая отличается большей устойчивостью и быстродействием от 2-ой системы. Недостаток: возможно компенсировать только те возмущения, которые мы можем измерить. Поэтому весьма эффективно во многих объектах

применение комбинированного управления (1-ое+2-ое). Пример: управление генераторами на эл/станции.

5

1) Основные принципы регулирования. Принцип компенсации

В основе алгоритма упр-ния заложены 3 фундаментальных принципа:

1) Принцип разомкнутого управления;

2) Принцип обратной связи;

3) Принцип компенсации (регулирование по возмущению);

3) Принцип компенсации (регулирование по возмущению):

_f = F(g,f)

g = F₁(f) _f = 0 – в установившемся режиме по принципу компенсации (отклонение должно отсутствовать)

При сравнении системы регулирования по возмущению с системой управления, то 1-ая отличается большей устойчивостью и быстродействием от 2-ой системы. Недостаток: возможно компенсировать только те возмущения, которые мы можем измерить.

2) Статическое и астатическое регулирование.

Системы стабилизации, программного управления и следящие системы можно разделить на 2 группы:

1 – статические;

2 - астатические;

1) 2)



САР будет статической по отношению к возмущающему или управляющему воздействиям, постоянной величине, отклонению регулируемой величины.

САР явл-ся астатической по возмущению и управляющему воздействию, если при стремлении возмущающего управ. воздействия постоянной величины отклонения регулируемая величина стремится к нулю и не зависит от величины приложенного воздействия. Одна и та же САР может быть астатической по управлению и статической по возмущению, либо наоборот.

6

1)Классификация САУ. Системы стабилизации

САУ в зависимости от характера управляющего воздействия делится на 3 класса:

• 
  система стабилизации;
  
• 
  система программного регулирования;
  
• 
  следящая система;
  

1). В процессе работы системы стабилизации управляющее воздействие остается величиной постоянной. Основной задачей системы остается поддержание на постоянном уровне с допустимой ошибкой величины независимо от действующих возмущений.

Отклонение регулируемой величины явл-ся хар-ным для систем стабилизации и позволяет дать качественную оценку систем этого класса.



 = X₂(t₂) – X₁(t₁)

Система стабилизации явл-ся различного рода САУ, преднозначенные для регулирования скорости, напряжения, давления и т.д.

2) Классификация САУ. Следящие системы.

Следящая системаУправляющее воздействие явл-ся величиной переменной, матем. Описание его во времени не может быть установлено, т.е. неизвестен источник сигнала. Т.к. следящая система предназначена для воспроизведения на выходе управляющего воздействия с возможно большей точностью, то ошибка явл-ся характерной, по которой можно судить о динамических св-вах следящих систем.Ошибка в следящей системе – это сигнал, в зависимости от величины которого осуществляется управление исполнительного устройства объекта.

7

1).Классификация САУ. Системы программного управления.

Классификация САУ.

САУ в зависимости от характера управляющего воздействия делится на 3 класса:

• 
  система стабилизации;
  
• 
  система программного регулирования;
  
• 
  следящая система;
  

2). система программного регулирования.

Управляющее воздействие изм-ся по заранее установленному закону. Системы программного управления явл-ся системами воспроизведения. В этих системах основной задачей явл-ся по возможности более точное воспроизведение управляющего воздействия на выходе в виде соответствующих изменений управляемой величины. О точности упр-ющего воздействия системы судят по величине ошибки, к-рая определяется как разность м/у управляющим воздействием и регулируемой величиной в данный момент времени.


 = g(t₁) – X(t₁) – ошибка в момент времени t₁.

Системой программного управления может служить любая копировальная система.

2) Типовые нелинейные звенья

1.звено релейного типа

2. звено с кусочно-лминейной характеристикой

3. звено с криволинейной характеристикой

4. звено уравнение которого содержит произведение переменных или их производных и другие их комбинации

5. неленейный импульсный элемент

логическое звено

звенья описываемые кусочно-линейными диф-ми уравнениями, в том числе переменной структуры.

8

1) САР непрерывно импульсного и релейного действия.

В зависимости от вида сигнала различаются непрерывные, релейные (нелинейные) и импульсные САР. Особенностью непрерывной САР явл-ся то, что во всех элементах системы входные и выходные сигналы непрерывны. К числу непр-ных систем относятся системы с гармонической циркуляцией. При этом для передачи могут исп-ся амплитудное модулирование, частотное мод-е и фазовое мод-е колебаний.

Если структуре САР имеется хотя бы один элемент с нелинейной характеристикой, то такя система наз-ся релейной.

2)Показатели качества процессов регулирования.

1) Перерегулирование – это отношение разности σ = (_Xmax – X_уст)/ X_усn*100% перерегулирование характеризует колебания системы. Допустимый предел (25…30)%

2) Время регулирования характеризует быстроту уравновешивания системы. t_рег принимаем за момент окончания переходного процесса.(допускается отклонение ±5%)

3) Число колебаний регулируемой величины в течении времени переходного процесса. t_{регулир} характеризует колебания системы. (допускается не более 3-х полных колебаний)

Дополнительные показатели качества:

1) Собственная частота колебаний системы , где Т_к – период собственных колебаний системы.

2) Логарифмический декремент затухания Характеризует быстродействие системы, т.е., быстроту затухания колебательного процесса.

3) Максимальная скорость сигнала на входе . Данный показатель характеризует быстродействие системы.

Для замкнутой САР, имеющий колебательный переходный процесс, на основе указанных показателей качества можно установить область допустимых отклонений регулируемой величины.

9

1) Требования, предъявляемые к динамическим свойствам САУ

Изменение неизменной величины во времени определяет переходный процесс и представляет собой динамическую характеристику по которой можно судить о качестве работы системы. Чтобы качественно выполнять задачу регулирования в различных условиях система должна обладать определенным запасом устойчивости, а также точн., кач.

2) Устойчивость импульсных систем. Критерий Раусса-Гурвица.

Устойчивость линейных систем

В процессе работы на систему действуют различные возмущающие силы, вызывающие ее отклонение от заданного закона движения. Если под влиянием возмущения система отклонилась от состояния равновесия и после прекращения действия внешнего возмущения снова вернулась в исходное состояние, то такая система устойчива.

Если под влиянием внешнего возмущения система будет отклоняться от состояния равновесия, а после прекращения действия возмущения система не возвращается в исходное состояние, а удаление системы с течением времени возрастает, то такая система называется неустойчивой.

В линейных системах отклонение при неустойчивом движении будет неограниченно возрастать.

Необходимое и достаточное условие устойчивости является выполнение требования, в соответствии с которым характеристическое уравнение системы должно иметь отрицательную вещественную часть. Наличие среди корней характеристического уравнения хотя бы одного корня с положительной вещественной частью свидетельствует о невыполнении этого условия, т.е. приводит к неустойчивости системы.

Устойчивость в линейной системе характеризуется затуханием переходного процесса. Т.к. затухание переходного процесса в свою очередь определяется только корнем характеристического уравнения

и не зависит от воздействия, то устойчивость является внутренним свойством линейной системы.

Для определения устойчивости системы необходимому и достаточному условию нужно уметь находить корни характеристического уравнения. Это можно сделать просто для уравнения 1-го и 2-го порядков. Реальные системы десятых, сотых порядков. Поэтому для анализа устойчивости без нахождения корней характеристического уравнения, используют критерии устойчивости.

КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВЕЦА

Необходимым и достаточным условием устойчивости системы любого порядка без решения характеристического уравнения, по рассмотрению его коэффициентов, были сформулированы учеными Раусом и Гурвицом.

Руас сказал, что для выполнения условия устойчивости, а следовательно для расположения всех корней характеристического уравнения в левой полуплоскости , необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.

Гурвец дополнил, что для выполнения условия устойчивости, а следовательно, для расположения вех корней характеристического уравнения в левой полуплоскости, необходимо и достаточно, чтобы все n диагональных миноров матрицы были положительны.

Критерий устойчивости Рауса и Гурвеца является алгебраическим, т.к. при их использовании задача определения знаков вещественных частей хар. уравнения сводится к выполнению общих алгебраических операций.