Диплом. Сацицкий. 1 анализ силовых схем российских электровозов с асинхронным тяговым приводом
 Скачать 6.03 Mb. Скачать 6.03 Mb.
|
|
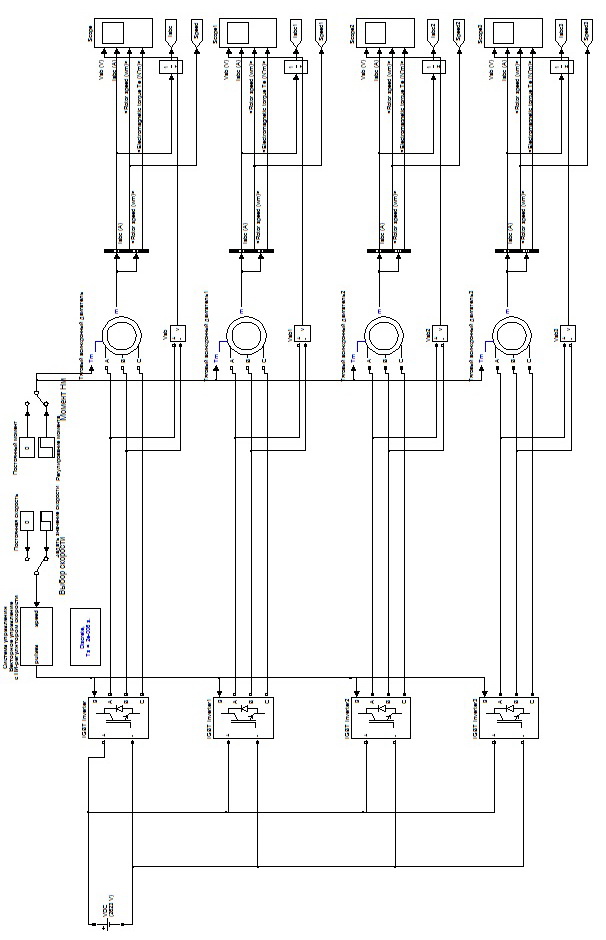
2.3 Проектирование силовой цепи электровоза 2ЭС5 Согласно технической документации, одна секция локомотива 2ЭС5 имеет четыре тяговых двигателя, которые получают питание от индивидуального источника трехфазного напряжения. Для моделирования силовой цепи электровоза на одном рабочем поле программы Matlab устанавливаются четыре модели асинхронных двигателей (Тяговый асинхронный двигатель–Тяговый асинхронный двигатель 3), которые будут получать электрическое питание от четырех трехфазных инверторов (IGBT Inverter). В свою очередь, инверторы получают электрическую энергию от источника постоянного тока. В виртуальной силовой схеме электровоза 2ЭС5 (рисунок 2.9) применяется общий генератор импульсов (Pulse Generator), а также общее заземление (Ground). Это упрощение позволяет исключить загромождение электрической схемы, а также компьютерная модель будет быстрее загружаться при моделировании.
3 СОЗДАНИЕ КОМПЬЮТЕРНЫХ МОДЕЛЕЙ СИСТЕМЫ УПРАВЛЕНИЯ ЭЛЕКТРОВОЗОВ 3.1 Анализ системы управления асинхронным приводом Системы регулирования скорости двигателя постоянного тока достаточно просты, но слабым местом такого электропривода является электродвигатель. Он дорог и ненадежен. При работе происходит искрение щеток, под воздействием электроэрозии изнашивается коллектор. Такой электродвигатель не может использоваться в запыленной и взрывоопасной среде. Асинхронные электродвигатели превосходят двигатели постоянного тока по многим параметрам: они просты по устройству и надежны, так как не имеют подвижных контактов. Они имеют меньшие по сравнению с двигателями постоянного тока размеры, массу и стоимость при той же мощности. Асинхронные двигатели просты в изготовлении и эксплуатации. Основной недостаток асинхронных электродвигателей – сложность регулирования их скорости традиционными методами (изменением питающего напряжения, введением дополнительных сопротивлений в цепь обмоток). Управление асинхронным электродвигателем в частотном режиме до недавнего времени было большой проблемой, хотя теория частотного регулирования была разработана еще в тридцатых годах. Развитие частотно-регулируемого электропривода сдерживалось высокой стоимостью преобразователей частоты. Появление силовых схем с IGBT-транзисторами, разработка высокопроизводительных микропроцессорных систем управления позволило различным фирмам Европы, США и Японии создать современные преобразователи частоты доступной стоимости. Для осуществления возможности регулирования момента и скорости в современных электроприводах используются следующие методы частотного управления, такие как: - векторное; - скалярное. Наибольшее распространение в приводах компрессоров, вентиляторов, насосов и прочих механизмов получили асинхронные электроприводы со скалярным управлением. Однако для вращения более мощного агрегата (например, тяговый двигатель электровоза переменного тока) в мире применяется векторное управление с широтно-импульсной модуляцией. Преимущества векторного метода управления асинхронным двигателем: - высокий уровень точности при регулировании скорости вращения вала, несмотря даже на возможное отсутствие датчика скорости; - осуществление вращения двигателя на малых частотах происходит без рывков, плавно; - если установлен датчик скорости, то можно достичь номинального значения момента на валу даже при нулевом значении скорости; - быстрое реагирование на возможное изменение нагрузки – резкие скачки нагрузки практически не отражаются на скорости электропривода; - высокий уровень КПД двигателя, за счет сниженных потерь из-за намагничивания и нагрева. Несмотря на очевидные преимущества, метод векторного управления имеет и определенные недостатки – большая сложность вычислений, для работы необходимо знание параметров двигателя. Однако именно векторный способ регулирования позволяет регулировать момент на валу двигателя, изменять скорость по жесткой характеристике двигателя. Поэтому, в качестве способа регулирования асинхронным приводом электровоза 2ЭС5 «Скиф» принимается векторное регулирование. 3.2 Векторное управление асинхронным приводом с широтно-импульсной модуляцией Широтно-импульсная модуляция (ШИМ) – это способ реализации вектора напряжения статора, применяемый в подавляющем большинстве систем векторного регулирования. Известно, что регулирование частоты вращения исполнительных механизмов можно осуществлять при помощи различных устройств: механических вариаторов, гидравлических муфт, дополнительно вводимыми в статор или ротор резисторами, электромеханическими преобразователями частоты, статическими преобразователями частоты. Применение первых четырех устройств не обеспечивает высокого качества регулирования скорости, неэкономично, требует больших затрат при монтаже и эксплуатации. Статические преобразователи частоты являются наиболее совершенными устройствами управления асинхронным приводом в настоящее время. Принцип частотного метода регулирования скорости асинхронного двигателя заключается в том, что, изменяя частоту питающего напряжения, можно в соответствии с выражением 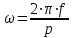 , (3.1) , (3.1)где p – число пар полюсов двигателя; При неизменном числе пар полюсов возможно изменять угловую скорость магнитного поля статора. Этот способ обеспечивает плавное регулирование скорости в широком диапазоне, а механические характеристики обладают высокой жесткостью. Регулирование скорости при этом не сопровождается увеличением скольжения асинхронного двигателя, поэтому потери мощности при регулировании невелики. Для получения высоких энергетических показателей асинхронного двигателя – коэффициентов мощности, полезного действия, перегрузочной способности – необходимо одновременно с частотой изменять и подводимое напряжение. Закон изменения напряжения зависит от характера момента нагрузки  . При постоянном моменте нагрузки напряжение на статоре должно регулироваться пропорционально частоте: . При постоянном моменте нагрузки напряжение на статоре должно регулироваться пропорционально частоте: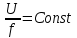 . (3.2) . (3.2)Таким образом, для плавного бесступенчатого регулирования частоты вращения вала асинхронного электродвигателя, преобразователь частоты должен обеспечивать одновременное регулирование частоты и напряжения на статоре асинхронного двигателя. Большинство современных преобразователей частоты построено по схеме двойного преобразования. Они состоят из следующих основных частей: звена постоянного тока (неуправляемого выпрямителя), силового импульсного инвертора и системы управления. Звено постоянного тока состоит из неуправляемого выпрямителя и фильтра. Переменное напряжение питающей сети преобразуется в нем в напряжение постоянного тока. Широтно-импульсное управление характеризуется периодом модуляции, внутри которого обмотка статора электродвигателя подключается поочередно к положительному и отрицательному полюсам выпрямителя. Длительность этих состояний внутри периода ШИМ модулируется по синусоидальному закону. Рассмотрим схему трехфазного инвертора для питания асинхронного двигателя. Такие устройства широко применяются для регулирования частоты вращения электродвигателей переменного тока. Для получения напряжения на статоре двигателя с низким содержанием высших гармоник, применяют широтно-импульсный способ формирования выходного напряжения инвертора. Для поддержания заданной скорости вращения вала двигателя можно реализовать обратную связь по скорости и регулировать частоту питающего напряжения (скалярное управление с применением датчиков обратной связи). Основным недостатком такой системы управления является плохая динамика регулирования, этого недостатка лишен метод векторного управление. Асинхронный двигатель питается от трехфазного IGBT инвертора с ШИМ модуляцией, который построен с использованием блока «универсальный мост». Контур управления скоростью в системе управления использует пропорционально-интегральный контроллер для получения в системе DQ-координат значения тока Iq (quadrature-axis), посредством которого контролируется крутящий момент двигателя. С помощью значения тока Id (direct-axis) регулируется магнитный поток. Блок DQ-ABC используется в качестве преобразователя трехфазной системы координат в систему координат DQ для регулятора тока. Блок преобразования координат из координатной системы ABC в ортогональную систему dq, используется практически во всех системах векторного управления и предназначен для прямого преобразования переменных. Преобразование координат осуществляется по следующим уравнениям: 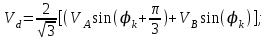 (3.3) 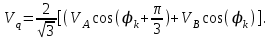 С помощью преобразования Парка для перевода стационарной системы координат в двухосную вращающуюся систему координат (id, iq), обладая информацией о реальных значениях в трехфазной системе ABC возможно получить данные в двухфазной системе dq (рисунок 3.1). 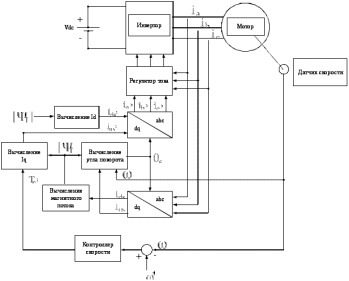 Рисунок 3.1 – Функциональная схема управления асинхронным двигателем с короткозамкнутым ротором Схема обеспечена визуализацией значений измеренных сигналов токов и напряжений в трехфазной цепи, а также на выходе блока "асинхронная машина" доступны такие данные как ток ротора, скорость и крутящий момент на валу двигателя. В конце времени моделирования система достигает своего устойчивого состояния. Асинхронный двигатель подключается к инвертору с ШИМ, который действует в качестве источника тока синусоидальной формы. Скорость двигателя ω сравнивается с опорным значением и ошибка обрабатывается регулятором скорости, чтобы произвести команду коррекции крутящего момента Te. Как будет показано ниже, поток ротора и вращающий момент может быть по отдельности под контролем статора по продольной оси тока и идентификаторами тока Iqs квадратурной оси соответственно (рисунок 3.2). 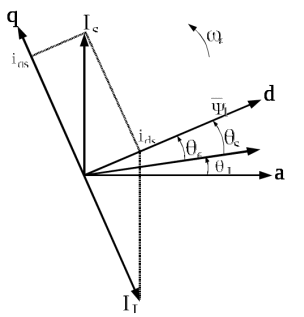 Рисунок 3.2 – Принцип управления с ориентацией по полю Ток статора Iqs (quadrature-axis) вычисляется из крутящего момента Te по формуле 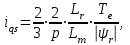 (3.4) (3.4)где 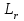 – индуктивность ротора; – индуктивность ротора;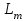 – взаимная индуктивность; – взаимная индуктивность;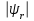 – текущее расчетное потокосцепление ротора. – текущее расчетное потокосцепление ротора.Контроллер пропорционально-интегрального типа используется как регулятор скорости, который поддерживает скорость двигателя равной заданной скорости в устойчивом состоянии и обеспечивает хорошую динамику во время переходных процессов. В реальном асинхронном двигателе ток статора формируется в неподвижной системе координат, поэтому его модель содержит внутренний блок вращения вектора тока или ротатор, с помощью которого осуществляется переход от неподвижной системы координат к системе d-q, ориентированной по потокосцеплению. Угол поворота вектора тока определяется частотой статора если в качестве опорного вектора используется потокосцепление ротора и по нему ориентирована координатная система. Модель двигателя можно задать избыточной системой математический уравнений с использованием 3-х фазной системы напряжений и токов. Однако целесообразно свернуть 3 величины в 2 с помощью обратимого алгоритма преобразования Кларка. Преобразование Кларка позволяет представить фазные токи и напряжения в качестве постоянных величин а не в виде значений переменных во времени. Это производится путем замены синусоидальной трехфазной системы питания двигателя на вращающуюся систему координат. Таким образом, переменные значения токов и напряжений сводятся к постоянным величинам с помощью преобразования Парка, которое и позволяет представить трехфазную асинхронную машину переменного тока как двигатель постоянного тока. Система управления контролирует сразу 2 параметра: - стабилизирует ток намагничивания на постоянном значении, обеспечивая необходимый уровень магнитного поля в двигателе. - регулирует при этом Iqs , для обеспечения необходимого момента на валу. Благодаря такому подходу асинхронная машина по характеристикам управления становится похожей на способ управления двигателем постоянного тока с независимым возбуждением. Так как система контролирует одновременно два тока то такая система управления называется векторной. В системе управления находится два ПИД-регулятора, которые регулируют соответствующий ток статора, изменяя напряжения и пересчитываются обратно с помощью преобразования Парка и Кларка (инверсных) в переменные значения напряжений трехфазной сети (которые делаются алгоритмом ШИМ). Преобразования Парка вращает систему координат, а инверсное преобразование Парка использует скорость вращения системы координат. Этой скоростью является синхронная скоростью вращения – скорость вращения синхронного двигателя, включенного в ту же электрическую сеть питания, что и асинхронный. Скорость равна скорости вращения ротора асинхронного двигателя с добавлением скорости скольжения. Для этого требуется: - точное измерение скорости вала, - вычисление скорости скольжения. Скорость ротора измеряется с помощью датчика инкрементального энкодера. Величина скольжения – определяется по модели двигателя. Так как подать напряжение на двигатель, не зная частоты, которая в свою очередь определяется скольжением невозможно, то нельзя просто измерить скорость скольжения. Поэтому модель двигателя предсказывает какое скольжение должно быть в данный момент т.е. модель работает на опережение. Скорость регулируется другим ПИД-регулятором, который вычисляет рассогласование между уставкой (заданное значение) скорости и ее текущим значением по датчику скорости и изменяет при этом ток Iqs, влияющий на момент. Системой используется зависимость: что скорость является интегралом момента. Поэтому система управления называется векторное управление с ориентированием по полю ротора (indirect field oriented control). Этот алгоритм векторного управления в настоящее время наиболее популярен. Алгоритм управления показан на рисунке 3.3. 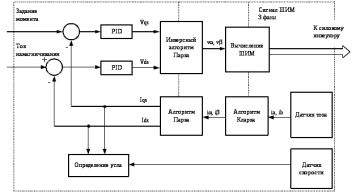 Рисунок 3.3 – Алгоритм векторного управления с ориентированием по полю ротора Модель построена с использование библиотечной модели асинхронного двигателя из дополнения Toolbox Simulink к пакету прикладных программ MATLAB. Проведение компьютерных экспериментов электромеханических процессов, протекающих в частотно-регулируемых электроприводах с ПИ‑контроллером скорости и алгоритмом векторного управления, является допустимым и оправданным при внедрении дополнительных корректирующих блоков для реализации управления по вектору главного потокосцепления Ψ0 и стабилизации модуля |Ψ0|. Эта модель дискретизируется с использованием интервала времени 2 мкс (рисунок 3.4). 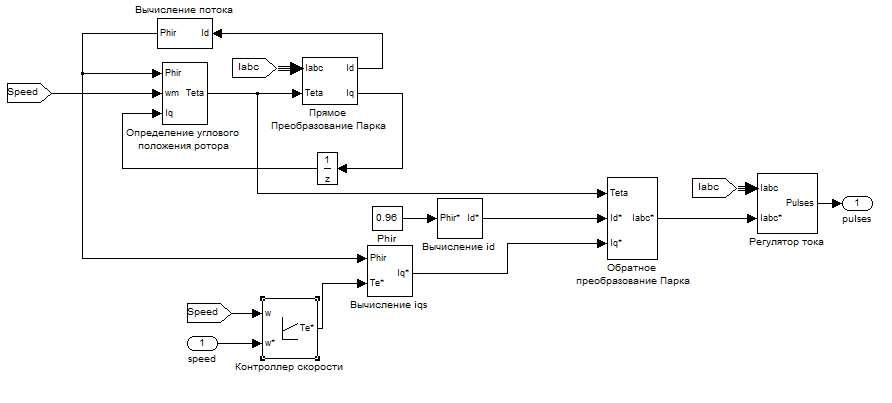 Рисунок 3.4 – Модель системы управления с ПИ-контроллером скорости Регулятор тока в векторном блоке управления состоит из трех контроллеров гистерезиса и построен с Simulink блоками (рисунок 3.5). 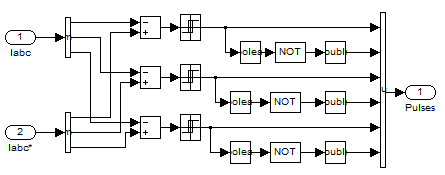 Рисунок 3.5 – Регулятор тока Блок преобразования координат по полученным значениям входных синусоидальных токов трёхфазной системы и угла поворота ротора вычисляет величины координат в систему direct axis и нулевой последовательности в двухосной вращающейся системе отсчета для трехфазного синусоидального сигнала, при этом используется следующее выражения: 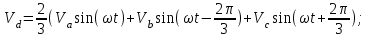 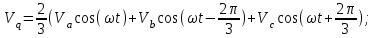 (3.5) (3.5)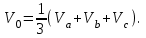 где  = скорость вращения (рад/с) вращающейся системы координат. = скорость вращения (рад/с) вращающейся системы координат.Блок обратного преобразования в Matlab представлен на рисунке 3.6. 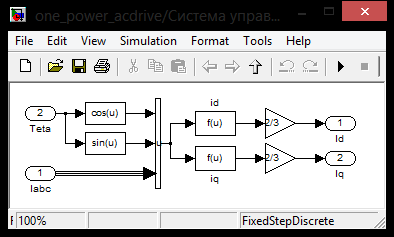 Рисунок 3.6 – Обратное преобразование Парка Блок выполняет обратное преобразование Парка. Он преобразует три величины: прямой оси, квадратичной оси и компоненты нулевой последовательности, выраженные в двухосной системе координат обратно в фазовые значения. Преобразование является одинаковым для тока и напряжения просто необходимо заменить значения Va, Vb, Vc, Vd, Vo на переменные Ia, Ib, Ic, Id, Iq и I0. Токи Id и Iq представляют являются токами протекающими в двух эквивалентных обмотках ротора (D обмотки на той же оси, что и поле обмотки, а Q обмотки в квадратичной оси), производящих один и тот же поток, что и токи статора Ia, Ib, Ic. Вычисление потока производится с помощью функции дискретного фильтра нижних частот первого порядка (рисунок 3.7). 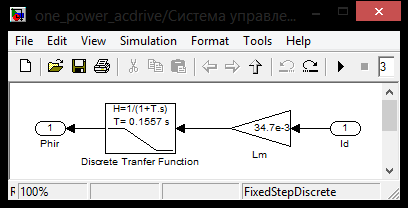 Рисунок 3.7– Вычисление потока Скорость двигателя обеспечивается выходом измерительного блока асинхронной электрической машины (рисунок 3.8). 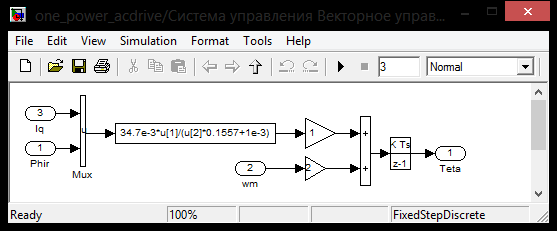 Рисунок 3.8 – Регулятор скорости двигателя Окно настройки параметров дискретного интегратора времени представлен на рисунке 3.9. 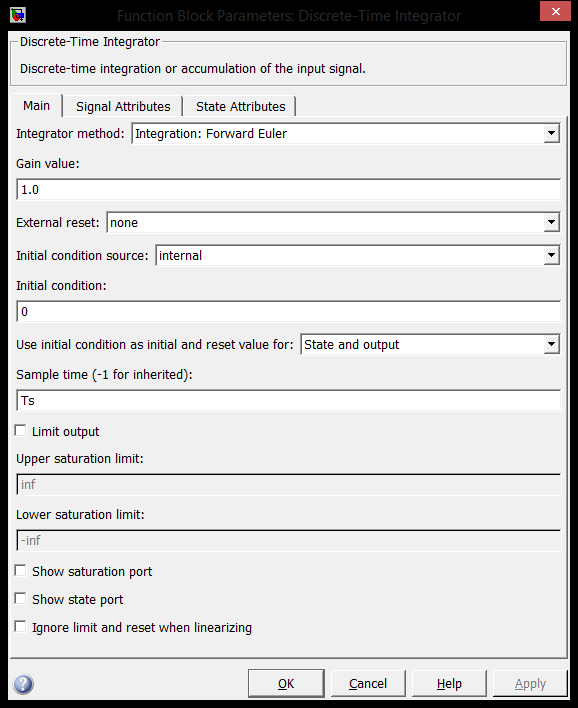 Рисунок 3.9 – Параметры дискретного интегратора времени Блок контроллера скорости представлен на рисунке 3.10. 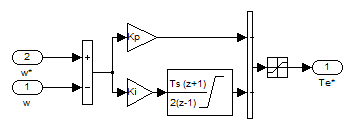 Рисунок 3.10 – Блок контроллера скорости Регулятор скорости пропорционально-интегрального типа реализуется с использованием Simulink блоков и производит вычисление значения величины рассогласования заданной и текущей измеренной скорости полученной на входе блока от асинхронной машины. Настройка параметров ПИ регулятора производится в диалоговом окне по следующим коэффициентам. Окно настройки параметров ПИ регулятора представлен на рисунке 3.11. 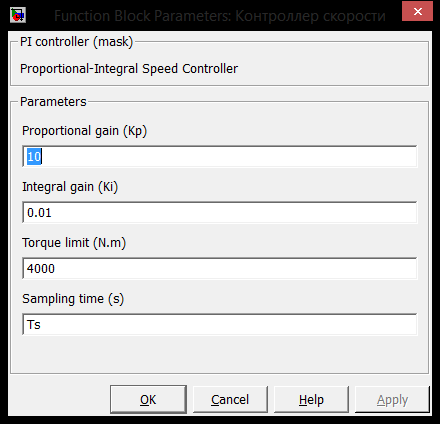 Рисунок 3.11 – Окно настройки параметров ПИ регулятора 4 ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТОВ НА КОМПЬЮТЕРНЫХ МОДЕЛЯХ 4.1 Теоретические основы процессов, происходящих при движении подвижного состава Тяговые расчёты используются при: проектировании железных дорог, проектировании подвижного состава, организации эксплуатации локомотивов, организации движения поездов. При расчётах используются упрощения: поезд принимается за материальную точку, масса поезда считается равномерно распределённой по его длине, железнодорожный путь в плане считается состоящим из прямых участков и дуг окружностей постоянного радиуса, длина переходных кривых включается в общую длину криволинейного участка, продольный профиль железнодорожного пути считается состоящим из прямолинейных отрезков и наличие между ними сопряжений не учитывается. Сила тяги локомотива зависит от скорости и определяется по тяговым характеристикам, которые строятся в соответствии с характеристиками тяговых двигателей. Сила тяги локомотива не превосходит силы сцепления ведущих колёс локомотива с рельсами. Коэффициент сцепления на стоянке максимален и убывает при возрастании скорости движения. Коэффициент сцепления зависит от многих случайных факторов: состояние пути, атмосферные условия Его заменяют расчётным коэффициентом сцепления ψK, определяемым по эмпирическим формулам, основанным на результатах экспериментов в реальной эксплуатации. Сопротивление движению – это сила, приложенная в точках касания колёс с рельсами, на преодоление которой затрачивается такая же работа, как на преодоление всех неуправляемых сил, препятствующих движению. Основное сопротивление – это силы, препятствующие движению локомотива по прямому горизонтальному пути на открытой местности при нормальных метеоусловиях с любой скоростью. Виды сопротивления: - сопротивления от трения в буксовых подшипниках; - сопротивление от трения качения колёс по рельсам; - сопротивление от трения скольжения колёс по рельсам; - рассеяния энергии при взаимодействии колёс с рельсами (потеря энергии на стыках и неровностях пути, упругая деформация рельсов и шпал); - сопротивления воздушной среды; - рассеяния энергии в окружающую среду при вертикальных колебаниях подрессоренных частей подвижного состава и рывках по длине поезда. Из-за влияния различных факторов, установить аналитические зависимости для основного удельного сопротивления невозможно, значение получают экспериментальным путём. В результате обработки опытных данных получают эмпирические формулы и графики. Дополнительное сопротивление это временно действующие силы, возникающие в конкретных условиях эксплуатации подвижного состава: - от уклона профиля пути; - от кривизны пути; - от ветра; - от низкой температуры; - от тоннелей; - от подвагонных генераторов пассажирских вагонов. Дополнительное удельное сопротивление движению в кривых участках пути возникает по следующим причинам: - колёса одной колёсной пары проходят разный путь по наружному и внутреннему рельсу (конусность бандажей уменьшает эту разницу), что приводит к увеличению проскальзывания колёс; - за счёт действия центробежной силы гребни колёс прижимаются к внутренней боковой грани наружного рельса, что увеличивает силу трения скольжения; - тележки подвижного состава поворачиваются относительно оси кузова, в результате чего в опорах, шкворневых устройствах и буксах возникают силы трения скольжения. Уравнением движения поезда называется - дифференциальное уравнение, описывающее зависимость между ускорением и равнодействующей приложенных к поезду сил На поезд действует много различных постоянных и переменных сил, отличающихся по направлению и величине: сила тяжести локомотива и вагонов, сила тяги электровоза, а также силы сопротивления, инерции и др. Под действием этих сил одновременно с качением колес по рельсам имеет место виляние, галопирование, скольжение, наклон отдельных единиц подвижного состава в поезде. Для упрощения уравнения движения учитывают только поступательное и вращательное. Таких как, якорей тяговых электродвигателей, зубчатых передач и колесных пар. Этими факторами определяется характер движения. Алгебраическая сумма этих сил определяет равнодействующую силу: 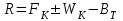 , (2.1) , (2.1)где 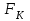 – сила тяги, кН; – сила тяги, кН;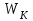 – сила сопротивления движению, кН; – сила сопротивления движению, кН;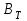 – тормозная сила, кН. – тормозная сила, кН.При проведении расчётов, требующих повышенной точности учитывается также скорость движения поезда. Процесс трогания с места подвижного состава после длительных стоянок (20 минут и более) происходит в условиях полусухого и сухого трения. За время стоянки разрушается масляный клин между трущимися деталями буксового подшипника, снижается температура и повышается вязкость смазки. Стоянка сопровождается значительным смятием металла в зоне контактной площадки, что увеличивает потери от трения качения по рельсам. Добавочное сопротивление при трогании с места для подвижного состава на подшипниках качения. Тормозная сила определяется как сумма произведений действительных сил нажатия тормозных колодок на действительные коэффициенты трения колодок. Для предотвращения юза тормозная сила, не должна превышать силу сцепления колёсной пары с рельсами. Тормозными задачами являются задачи определения тормозных средств и задачи определения расстояния, на котором поезд может остановиться или снизить скорость до заданного значения. Из-за инерционности тормозной системы увеличение тормозной силы в разных вагонах происходит не одновременно. Для упрощения расчётов принимается, что тормозная сила нарастает мгновенно до установившегося значения через некоторый отрезок времени tп, который называют временем подготовки тормозов к действию. Тормозной путь равен сумме подготовительного тормозного пути (расстояния, пройденного за время подготовки тормозов) и действительного пути торможения. Величина действительного пути торможения обычно определяется численным интегрированием уравнения движения по интервалам скоростей. 4.2 Моделирование процессов разгона электровоза 2ЭС5 Для проведения расчетов принимается, что максимальное тяговое усилие при трогании с места электровоза ограничено значением 833 кН. Разгон осуществляется при нескольких вариантах нагрузки. В первом варианте вращающий момент равен 8700 Нм (222 720 Н для электровоза). Это номинальный режим работы двигателя при скорости вращения 1038 об/мин (108 рад/с) при номинальной мощности 981 кВт, что соответствует скорости 120 км/ч. На рисунке 4.1 показан процесс разгона секции электровоза 2ЭС5 от 0 до 120 км/ч, при этом нагрузка на валу двигателя равна 8700 Нм. В данном примере проводится моделирование без учета нагрузки на двигатель от состава и локомотива. 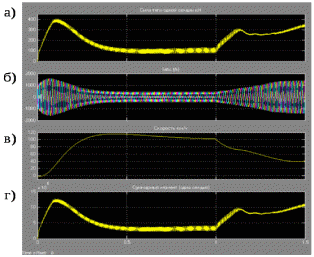 Рисунок 4.1 – Переходные процессы при разгоне электровоза с постоянной нагрузкой 8700 Нм: а) значение силы тяги, кН; б) ток нагрузки на тяговом двигателе, А; в) скорость движения электровоза, км/ч; г) значение суммарного электромагнитного момента секции электровоза, Нм На рисунке 4.1 присутствует ограничение силы тяги в 833 кН по условию трогания с места для данного электровоза. На графике представлен процесс разгона при номинальной нагрузке двигателя 8700 Нм от 0 до 120 км/ч и переход на скорость до 45 км/ч при нагрузке на валу электродвигателя 27000 Нм. На графике видно изменение тока статора двигателя от пускового значения к номинальному 430 А и до тока длительного (часового) режима электровоза. При этом сила тяги локомотива изменяется от 250 кНм до 690 кНм (от 125 до 390-395 кНм для одной секции). На рисунке 4.2 изображено моделирование процесса разгона с 45 км/ч при моменте сопротивления на валу двигателя 27000 Нм до 120 км /ч с последующим снижением нагрузки на валу электродвигателя до номинального значения равного 8700 Нм. На диаграмме трехфазных синусоидальных токов при этом отображено изменение амплитудного значения токов статора от пускового при высоких значения нагрузки на валу двигателя до номинального соответствующего моменту сопртивления на валу электродвигателя 8700 Нм. 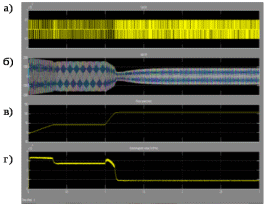 Рисунок 4.2 – Переходные процессы при разгоне электровоза от 45 до 120 км/ч: а) значение силы тяги, кН; б) ток нагрузки на тяговом двигателе, А; в) скорость движения электровоза, км/ч; г) значение суммарного электромагнитного момента секции электровоза, Нм На рисунке 4.3 показано моделирование процесса перехода от часового/длительного режима с реализуемой силой тяги 690 кН на скорости 45 км/ч с нагрузкой 27000 Нм и ограничением электромагнитного момента электродвигателя при трогании с места 32500 Нм к режиму максимальной скорости 120 км/ч и реализуемой силой тяги 250 кН при номинальном моменте сопротивления на валу тягового двигателя 8700 Нм. Из графиков токов видно переходной режим от пускового к номинальному. 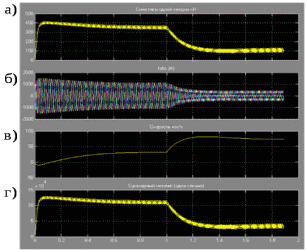 Рисунок 4.3 – Переходные процессы при разгоне электровоза с нагрузкой на валу двигателя 8700 Нм: а) значение силы тяги, кН; б) ток нагрузки на тяговом двигателе, А; в) скорость движения электровоза, км/ч; г) значение суммарного электромагнитного момента секции электровоза, Нм 4.3 Моделирование процессов торможения электровоза Первый эксперимент с торможением производится из условия движения локомотива с начальной скоростью 50 км/ч с ее снижением до 0 км/ч (до полной остановки) Процесс изменения тока нагрузки асихронного двигателя представлен на рисунке 4.4. В этом случае при отсутствии тока нагрузки снижается до нуля и скорость движения. 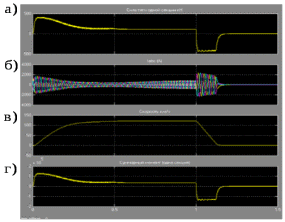 Рисунок 4.4 – Переходные процессы при торможении электровоза с 50 до 0 км/ч: а) значение силы тяги, кН; б) ток нагрузки на тяговом двигателе, А; в) скорость движения электровоза, км/ч; г) значение суммарного электромагнитного момента секции электровоза, Нм На рисунке 4.5 представлены переходные процессы при торможении, в которых при остановке локомотива на валу двигателя остается нарузка 8700 Нм. 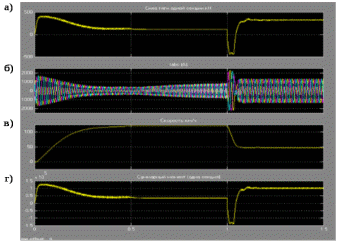 Рисунок 4.5 – Переходные процессы при торможении электровоза с остаточной нагрузкой: а) значение силы тяги, кН; б) ток нагрузки на тяговом двигателе, А; в) скорость движения электровоза, км/ч; г) значение суммарного электромагнитного момента секции электровоза, Нм На данном рисунке приводятся графики эксперимента, в котором производится торможение локомотива до 0 км/ч (до остановки) при условии сохранения нагрузки на валу двигателя. Из графиков видно отличие от предыдущего опыта, где при остановке электровоза ток двигателя опускался до 0 А, напротив в этом эксперименте после остановки по статорной обмотке двигателя протекает ток. На рисунке 4.6 представлены переходные процессы при торможении при повышенной нарузке на валу в 25000 кН (экстренное торможение). 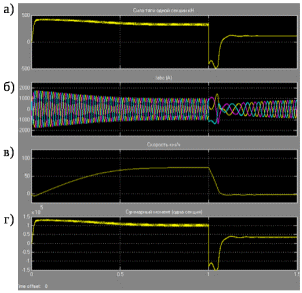 Рисунок 4.6 – Переходные процессы при экстренном торможении электровоза: а) значение силы тяги, кН; б) ток нагрузки на тяговом двигателе, А; в) скорость движения электровоза, км/ч; г) значение суммарного электромагнитного момента секции электровоза, Нм На данных графиках представлен эксперимент аналогичный предыдущему, отличием является большая нагрузка на валу электродвигателя, которая составляет для данного опыта 25000 Нм, что соответствует силе тяги локомотива 690 кН. На рисунке 4.7 изображен процесс торможения со 120 км/ч (номинальный режим двигателя) до 40 км/ч (часовой/длительный режим локомотива) при соответствующем увеличении нагрузки на валу электродвигателя от 8700 Нм до 27000 Нм. При этом диаграмма тока показывает изменение значений тока статора от номинального до тока часового/длительного режима локомотива. 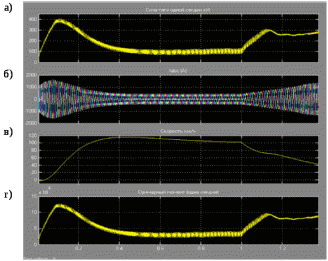 . Рисунок 4.7 – Переходные процессы при торможении электровоза с 120 до 40 км/ч: а) значение силы тяги, кН; б) ток нагрузки на тяговом двигателе, А; в) скорость движения электровоза, км/ч; г) значение суммарного электромагнитного момента секции электровоза, Нм Таким образом, проведенное моделирование доказывает адекватность разработанной системы управления асинхронным приводом, а также модели силовой цепи электровоза 2ЭС5. |