1. Цель и задачи курса теории механизмов и машин. Теория механизмов и машин

• Название: 1. Цель и задачи курса теории механизмов и машин. Теория механизмов и машин
• Дата: 09.03.2018
• Размер: 0.77 Mb.
• Имя файла: TMM.docx
• Тип: Документы; #38026
• страница: 2 из 5

Подвижность механизма – число независимых обобщенных координат, однозначно определяющее положение звеньев механизма на плоскости или в пространстве.

Связь – ограничение, наложенное на перемещение тела по данной координате.

Избыточные (пассивные) – такие связи в механизме, которые повторяют или дублируют связи, уже имеющиеся по данной координате, и поэтому не изменяющие реальной подвижности механизма. При этом расчетная подвижность механизма уменьшается, а степень его статической неопределимости увеличивается. Иногда используется иное определение: Избыточные связи – это связи, число которых в механизме определяется разностью между суммарным числом связей, наложенных кинематическими парами, и суммой степеней подвижности всех звеньев, местных подвижностей и заданной (требуемой) подвижностью механизма в целом.

Местные подвижности – подвижности механизма, которые не оказывают влияния на его функцию положения (и передаточные функции), а введены в механизм с другими целями (например, подвижность ролика в кулачковом механизме обеспечивает замену в высшей паре трения скольжения трением качения).

14. Структурный синтез плоских рычажных механизмов

Структурная группа (группа Ассура) – это такая кинематическая цепь, присоединение которой к любому механизму не изменяет его числа степеней свободы. При этом такая цепь не должна распадаться на более простые цепи с тем же свойством.

Метод структурного синтеза создан Ассуром, согласно котороыму любой плоский механизм может быть образован присоединением групп асура к механизмам первого класса

Каждый плоский рычажный механизм рассматривается как сложная система, состоящая из стойки, ведущих звеньев и ряда простейших наслоений. Количество ведущих звеньев определяется, как известно, числом степеней свободы механизма.

При структурном анализе плоских рычажных механизмов необходимо решить следующие вопросы: а) подсчитать число степеней свободы механизма и определить количество начальных звеньев; б) разложить механизм на структурные группы и механизм ( механизмы) первого класса; в) определить класс, порядок и вид каждой группы; г) определить класс механизма; д) составить формулу строения механизма.

Согласно этому методу схема плоского рычажного механизма, располагаемая в прямоугольной системе координат XOY, представляется как замкнутый многоугольник, состоящий в зависимости от сложности механизма из одного или нескольких замкнутых контуров. Условия замкнутости записывают в векторной форме или в виде проекций на оси координат.

15. Планы положений плоских рычажных механизмов

Независимые между собой параметры, однозначно определяющие положение и движение механической системы, называют обобщенными координатами. Количество обобщенных координат равно числу степеней свободы системы, поэтому, установив число степеней свободы механизма, необходимо выбрать столько же обобщенных координат. Как правило, в механизме с одной степенью свободы имеется одно начальное (входное) звено, поэтому за обобщенную координату обычно принимается или угол поворота вращающегося звена, или линейная координата прямолинейно движущегося звена.

Построение плана скоростей плоского механизма

Основу построения плана скоростей составляет векторная формула определения скорости точки плоской фигуры



Где Vp - скорость точки P, выбранной за полюс; V_mp - скорость точки М во вращательном движении плоской фигуры относительно полюса, величина которой равна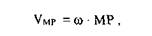

ω- угловая скорость плоской фигуры.

Чтобы воспользоваться векторной формулой, необходимо сначала построить в определенном масштабе, план механизма в заданном положении. Затем нужно выбрать масштабный коэффициент, который равен отношению скорости полюса к длине отрезка, изображающего эту величину. Для обеспечения требуемой точности построения длину отрезка принимают равной 40...60 мм:

 

После этого в выбранном масштабе строится векторный треугольник по уравнению (1.4), в котором вектор Vм является замыкающим вектором, а V_mp перпендикулярен к отрезку МР. Такие построения проводятся для всех характерных точек механизма (как правило, кинематических пар) на одном рисунке.

Построение плана ускорений плоского механизма

Основой построения плана ускорений служит векторная формула, определяющая ускорение точки плоской фигуры: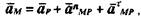

 

где a_p- ускорение точки, выбранной за полюс; aⁿ_MPи a^τ_MP - составляющие ускорения точки М во вращательном движении плоской фигуры вокруг полюса Р. При этом величины этих составляющих определяются по формулам

 

где ω и ε, соответственно, угловая скорость и угловое ускорение плоской фигуры.

Рассмотрим построение плана ускорений на том же самом примере плоского механизма, полагая что начальное звено 1 движется с постоянной угловой скоростью. В этом случае полное ускорение точки А равно его нормальной составляющей и направлено от точки А к оси вращения звена - точке О. По величине



16. Функцией положения механизма называется зависимость координаты выходного звена от обобщенных координат механизма. Для механизма, схема которого показана на рис. при начальном звене 1 и выходном
звене 5 функцию положения механизма можно получить в явном виде

φ₅ = φ₅(φ₁). Чаще, однако, функцию положения механизма удается получить только в неявном виде Φ(φ₁,φ₅)=О. В общем случае механизма с несколькими степенями свободы функция положения механизма в явном виде является функцией обобщенных координат

φ_n= φ_n(φ₁…., φ_s)

где n — индекс выходного звена, φ ₁, ... ,

φ _S — обобщенные координаты механизма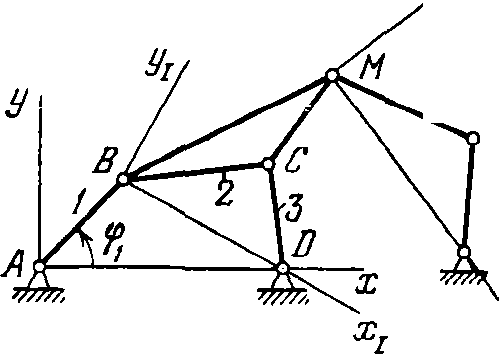



17. Передаточная функция механизма

- зависимость между параметрами движения или состояния рассматриваемого и входного звеньев механизма. Многие передаточные функции механизмов имеют собственные названия - передаточное отношение, силовое передаточное отношение, функция положения и т. д. 
 
 Кинематическими передаточными функциямимеханизма называются производные от функции положения по обобщенной координате. Первая производная называется первой передаточной функцией или аналогом скорости (обозначается), вторая - второй передаточной функцией или аналогом ускорения (обозначается).
♦  Переда́точная фу́нкция механи́зма
Для определённости рассмотрим механизм, у которого W=1.

Введём в рассмотрение первую и вторую передаточные функции механизма.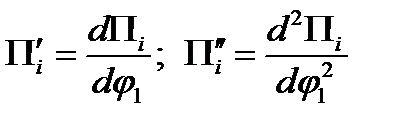

 .

Если 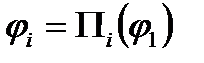 - угловая координата звена i, то первую передаточную функцию называют также аналогом угловой скорости, а вторую—аналогом углового ускорения звена i.



18. Планы скоростей плоских рычажных механизмов.

План скоростей строится для определения скоростей точек (кинематических пар, центров тяжести) и угловых скоростей звеньев механизма.

Построение плана скоростей начинается с того, что мы строим на чертеже механизм в стандартном масштабе, ставим на чертеже точку и обозначаем ее буквой «р» - это полюс плана скоростей, из этой точки выходят скорости всех точек механизма. Далее вычисляем скорость точки принадлежащей входному звену – как правило, кривошипу. Задаемся длинной отрезка соответствующего скорости этой точки, вычисляем масштаб плана скоростей. Потом составляем векторное уравнение для скорости точки – кинематической пары принадлежащей ближайшей к кривошипу группе Ассура. В соответствии с уравнением находим скорость этой точки, скорости остальных точек принадлежащих этой группе Ассура определяем по свойству плана скоростей.

Свойство плана скоростей:

Каждому звену механизма соответствует подобная ей фигура на плане скоростей, только повернутая под определенным углом и в другом масштабе. Т.е. звено треугольное – то на планах будет подобный ему треугольник. Таким образом, можно найти положение остальных точек на плане, составив элементарные пропорции.

После построения плана скоростей определяются искомые величины.


19. Планы ускорений плоских рычажных механизмов.



План ускорений - построение треугольников ускорений, выполненное на отдельном участке чертежа и произведенное из одной общей точки.

Полюсом плана ускорений называется произвольная точка плоскости чертежа, из которой производится построение плана ускорений.

Нормальное ускорение ведущего звена:



Нормальное ускорение направлено из точки к центру вращения.

Касательное ускорение:



При отсутствии углового ускорения касательное ускорение равно нулю.

Ускорение точки В определится из векторного уравнения:



Известны направление ускорения аⁿ_ВА - оно направлено вдоль шатуна АВ из точки В к точке А, и его величина:



Для ускорений а^_ВА и а_В известно только направление. Первое из них направлено перпендикулярно шатуну АВ, а второе вдоль направляющей ползуна.

Масштабом ускорений называется отношение нормального напряжения ведущего звена в м/с² к длине отрезка изображающего данное ускорение на плане ускорений в мм.



Свойства плана ускорений:

- Отрезки планов ускорений, проходящие через полюс, изображают абсолютные ускорения. Направление абсолютных ускорений всегда получается от полюса. В конце векторов абсолютных ускорений принято ставить малую букву той буквы, которой обозначена соответствующая точка на плане механизма;

- Отрезки плана ускорений, соединяющие концы векторов абсолютных ускорений, обозначают относительные ускорения;

- Концы векторов абсолютных ускорений точек механизма жестко связанных между собой на плане ускорений образуют фигуры подобные, сходственно расположенные и повернутые на угол 180- относительно расположения их на плане механизма;

- Постоянные неподвижные точки механизма имеют соответствующие им точки плана ускорений расположенные в полюсе;

20. Кинематический анализ механизмов.

Основной задачей кинематики механизмов является изучение движения звеньев механизмов вне зависимости от сил, действующих на эти звенья.

При кинематическом исследовании механизмов рассматриваются следующие основные вопросы:

1) построение планов скоростей;

2) построение траектории любой точки механизма;

3) определение скоростей и ускорений любой точки механизма, определение угловых скоростей и ускорений любого звена механизма, определение радиуса кривизны в любой точке траектории и др.

Кинематическое исследование можно вести как с применением графических методов, так и аналитическим путем. Графические методы исследования, давая достаточную для инженерной практики точность, обычно оказываются проще и нагляднее аналитических.

Когда ведется систематическое углубленное исследование какого-либо определенного типа механизма, более удобным оказывается аналитический метод. При графических построениях на чертеже приходится изображать не только длины звеньев, но и скорости и ускорения отдельных точек, а также и другие величины. В этих условиях удобно использовать масштабный коэффициент, которым называют отношение действительной величины к изображению. Например, для звена, имеющего длину (м) и изображенного на чертеже отрезком ab (мм), масштабный коэффициент длин будет равен
21. Кинематический анализ зубчатых механизмов.

Задачей кинематического анализа передач является нахождение передаточного отношения передачи через отношения размерных параметров ее звеньев.

Передаточным отношением от звена k к звену i называется отношение угловой скорости ωk (или числа оборотов в минуту nk) звена k к угловой скорости ωi (или числу оборотов в минуту ni) звена i, т.е.



Задачей кинематического анализа передач является нахождение передаточного отношения передачи через отношения размерных параметров ее звеньев.

22. Динамика машин и механизмов. Основные определения.

Динамика – раздел механики машин и механизмов, изучающий закономерности движения звеньев механизма под действием приложенных к ним сил. "Динамика рассматривает силы в качестве причины движения тел".

Динамика машин и механизмов решает следующие основные задачи: установление законов движения звеньев механизмов, регулирование движения звеньев, нахождение потерь на трение, определение реакций в кинематических парах, уравновешивание машин и механизмов.

В основе динамики лежат три закона, сформулированные Ньютоном, из которых следует:

Из первого закона: Если равнодействующая всех внешних сил, действующих на механическую систему равна нулю, то система находится в состоянии покоя.

Из второго закона: Изменение состояния движения механической системы может быть вызвано либо изменением действующих на нее внешних сил, либо изменением ее массы.

Из этих же законов следует, что динамическими параметрами механической системы являются:

1) массы m и моменты инерции I звеньев механизма – инерциальные параметры;

2) силы Fij и моменты сил Mij , приложенные к звеньям механизма - силовые параметры;

3) линейные a ускорения точек звеньев и угловые e ускорения звеньев - кинематические параметры.

В общей постановке динамика - изучение каких-либо процессов или явлений в функции времени. Динамическая модель - модель системы, предназначенная для исследования ее свойств в функции времени (или модель системы, предназначенная для исследования в ней динамических явлений).

Прямая задача динамики - определение закона движения системы при заданном управляющем силовом воздействии.

Обратная задача динамики - определение требуемого управляющего силового воздействия, обеспечивающего заданный закон движения системы.

Методы составления уравнений (динамической модели системы):

энергетический (уравнения энергетического равновесия - закон сохранения энергии); кинетостатический (уравнения силового равновесия с учетом сил инерции по принципу Д’Аламбера).

23. Механическая работа, энергия и мощность.

Работа – интеграл скалярного произведения вектора силы F на вектор элементарного приращения перемещения точки ее приложения dS.



где sk, s0 – конечное и начальное перемещение точки приложения силы F,

(F,dS) – острый угол между вектором силы F и вектором перемещения точки ее приложения dS.