1. Цель и задачи курса теории механизмов и машин. Теория механизмов и машин
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
Энергия – способность системы совершать работу или запас работы. Любая работа совершаемая над системой увеличивает его энергию. В механических системах различают кинетическую и потенциальную энергии. Чтобы сообщить системе ускорение и заставить ее двигаться с требуемой скоростью, нужно совершить работу. Эта работа запасается системой в виде энергии движения или кинетической энергии. Для механической системы, в которой r звеньев вращаются, p совершают поступательное движение и k - плоское, кинетическая энергия равна: 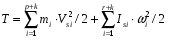 где mi - масса i-го звена, Vsi - скорость центра масс i-го звена, Isi - момент инерции i-го звена относительно его центра масс, wi - угловая скорость i -го звена. Перемещение системы или ее элемента в потенциальном поле из точки с низким потенциалом в точку с более высоким или деформация звена системы требует совершения работы, которая запасается системой в виде потенциальной энергии. Для системы, в которой a звеньев подвергаются скручиванию и s звеньев - линейной деформации, потенциальная энергия деформации равна: 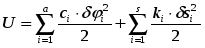 где ci - крутильная жесткость i -го звена, δϕi - угловая деформация i -го звена, ki - линейная жесткость i -го звена, δsi - линейная деформация i - го звена. Мощность – производная от работы по времени. Средняя мощность – отношение совершенной работы ко времени ее выполнения. Рассмотрим механическую систему на которую воздействуют m моментов и f сил. Её мощность: 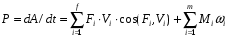 24. Силы, действующие в механизмах, и их характеристики. Все силы, действующие в механизмах, условно подразделяются на: 1. Внешние, действующие на исследуемую систему со стороны внешних систем и совершающие работу над системой. Эти силы в свою очередь подразделяются на: 1) движущие, работа которых положительна (увеличивает энергию системы); 2) сопротивления, работа которых отрицательна (уменьшает энергию системы). Силы сопротивления делятся на: - силы полезного (технологического) сопротивления - возникающие при выполнении механической системы ее основных функций (выполнение требуемой работы по изменению координат, формы или свойств изделия и т.п.); - силы трения (диссипативные) - возникающие в месте связи в КП и определяемые условиями физико-механического взаимодействия между звеньями (работа всегда отрицательна); 3) взаимодействия с потенциальными полями (позиционные) - возникают при размещении объекта в потенциальном поле, величина зависит от потенциала точки, в которой размещается тело (работа при перемещении из точки с низким потенциалом в точку с более высоким - положительна; за цикл, т.е. при возврате в исходное положение работа равна нулю). Потенциальное поле - силы тяжести или веса. Существуют электромагнитные, электростатические и другие поля. 2. Внутренние, действующие между звеньями механической системы. Работа этих сил не изменяет энергии системы. В механических системах эти силы называются реакциями в кинематической паре. 3. Расчетные (теоретические) - силы, которые не существуют в реальности, а только используются в различных расчетах с целью их упрощения: 1) силы инерции - для силового расчета подвижных механических систем. При добавлении этих сил к внешним силам, действующим на систему, устанавливается квазистатическое равновесие системы и ее можно рассчитывать, используя уравнения статики (метод кинетостатики). 2) приведенные (обобщенные) силы – силы, совершающие работу по обобщенной координате равную работе соответствующей реальной силы на эквивалентном перемещении точки ее приложения. 25, Динамическая модель машинного агрегата Машинный агрегат - это, преимущественно, совокупность машины-двигателя, механизма передач и рабочей машины. Это, как правило, Многозвенная система, нагруженная многими силами и моментами, приложенными к различных звеньев. На рис. 4.1 в качестве примера приведена силовая установка, в которой ДВС приводит в движение через зубчатую передачу вал рабочей машины - центробежной помпы. К звеньям машинного агрегата при движении приложены различные силы: движущая сила Fд, сила полезного сопротивления - момент МРМ, силы тяжести, во всех кинематических парах действуют силы трения. При этом каждое звено имеет свою массу, момент инерции. Своими действиями приложенные силы придают механизму тот или иной закон движения. Динамическая модель механизма, или машины представляет собой уравнение движения звена приведения, к которому приведены все силы и массы звеньев. В случае, если звено приведения совершает вращательное движение то уравнение движения принимает вид: 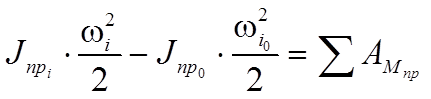 где Jпр – приведенный момент инерции звена приведения; Мпр – приведенный момент сил звена приведения. В случае, если звено приведения совершает поступательное движение уравнение движения имеет вид: 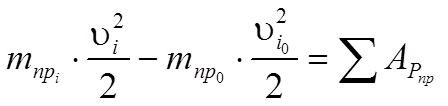 где mпр – приведенная масса звена приведения; Рпр – приведенная сила звена приведения. 26. Приведение сил в механизмах При исследовании движения механизма удобно все силы, действующие на звенья, заменить силами, приложенными к одному звену. При этом надо чтобы работа на рассматриваемом возможном перемещении или мощность, развиваемая замещаемыми силами, равнялась сумме работ или мощностей, от сил, приложенных к звеньям механизма. Звено, к которому приложены приведенные силы, - звено приведения, а точка приложения приведенных сил – точки приведения. Механизм с 1 степенью свободы, для изучения его движение достаточно знать закон движения одного его звена. Звеном приведения выбирают обычно, то звено, по обобщенной координате которого проводится исследование механизма. Например, кривошип, координата угол фи. Графический способ. Строится план возможных скоростей, который может быть построен без знаний закона движения. Метод имеет ограниченную точность, но с помощью плана, можно найти всегда положение скорости. Суммарную приведенную силу или момент удобно записывать в виде составляющих, например: М∑пр=∑МFiпр+∑ММiпр, где каждая составляющая определяется из соответствующего равенства мощностей: МFiпр=Fi·Vi/ω·cos(FiVi) - для силы Fi; ММiпр=Мi·ωi/ω - для момента Мi; Как видно из формул, величина Fпр (Мпр) зависит лишь от соотношения скоростей, а не от их абсолютной величины, что позволяет для приведения сил использовать планы скоростей без учета их масштабов. Каждое i-ое звено механизма обладает массой mi и моментом инерции Ji относительно оси, проходящей через центр масс звена, при этом кинетическая энергия i-го звена плоского механизма равна: Ti=(mi·Vi2/2)+Ji·ωi2/2 27. Приведение масс в механизмах Приведенная масса (момент инерции) – такая условная масса (момент инерции), обладая которой главное звено имеет кинетическую энергию, равную сумме кинетических энергий приводимых масс и моментов инерции: 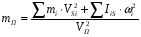 Где mi – масса i-го звена, Vsi – скорость центра масс i-го звена, Iis – момент инерции i-го звена относительно оси, проходящей через центр масс. В случае, когда массы звеньев приводятся к звену, совершающему вращательное движение относительно стойки, целесообразно пользоваться понятием приведённого момента инерции Iп этих масс относительно оси вращение звена приведения. Приведённый момент инерции равен: 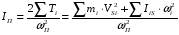 Величины Iп и mп связаны равенством:  Где l – расстояние между точкой приведения и осью вращения звена приведения. Из формул следует, что приведённая сила или приведённый момент сил зависят от отношения скоростей ведомых звеньев и скорости звена приведения, приведённая масса и приведённый момент инерции зависят от отношения квадратов этих же скоростей. 28. Уравнения движения механизма. Для определения законов движения начальных звеньев за заданными силами используются уравнения, которые называются уравнениями движения механизма. Число этих уравнений равняется числу степеней подвижности механизма. Уравнения движения механизма могут быть представлены в разных формах. Для механизмов с одной степенью вольности одна из самых простых форм уравнений получается на основе теоремы об изменении кинетической энергии: изменение кинетической энергии механизма на некотором перемещении равняется сумме работ всех сил, которые действуют на звенья механизма на этом самом перемещении. Данный закон представлен в виде уравнения: 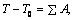 (1) (1)где Т — кинетическая энергия механизма в произвольном положении; Т0 — кинетическая энергия механизма в положении, которое принимается за начальное; 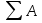 — сумма алгебраизма работ всех сил и моментов, которые прилагаются к механизму на некотором перемещении. — сумма алгебраизма работ всех сил и моментов, которые прилагаются к механизму на некотором перемещении.Работу осуществляют все активные силы и моменты и силы трения во всех кинематических парах механизма. Уравнение движения в энергетической форме. Сведем все силы и моменты механизма с одной степенью вольности к одному звену возведения, то есть заменим рассматриваемый механизм его динамической моделью. Поскольку вся нагрузка, прилагаемая к модели, выражается возведенным моментом МЗВ, то правая часть уравнения (1) равняется 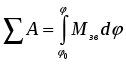 ; ; 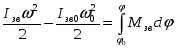 (3) (3)Уравнение (3) называют уравнением движения механизма в энергетическом виде, или — в форме уравнения кинетической энергии. В целом верхний предел интегрирования в (3) считается переменной. 29. Режимы движения машины. В зависимости от того какую работу совершают внешние силы за цикл движения машины различают три режима движения: разгон, торможение и установившееся движение. Циклом называют период времени или период изменения обобщенной координаты, через который все параметры системы принимают первоначальные значения. Установившимся движением механизма называют такое движение, при котором его обобщенная скорость и кинетическая энергия являются периодическими функциями времени. Минимальный промежуток в начале и в конце которого повторяются значения кинетической энергии и обобщенной скорости механизма – называют временем цикла установившегося движения. Для идеальной механической системы, в которой нет потерь энергии и звенья абсолютно жесткие при получении уравнений движения механизма можно воспользоваться теоремой об изменении кинетический энергии: разность энергии за какой либо промежуток времени равна работе сил за тот же промежуток времени. 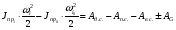 где Ад.с. – работа движущих сил; Ап.с. – работа сил производственных сопротивлений; Ав.с. – работа сил вредных сопротивлений (трения и внешней среды); АG – работа сил веса. Для режима разгона: wi0 = 0, Ап.с. = 0, тогда:  Работа движущих сил при разгоне расходуется кинетическую энергию, работу сил вредных сопротивлений и веса. Для режима выбега: wi = 0, Ад.с. = 0, Ап.с. = 0 тогда: Работа движущих сил при разгоне расходуется кинетическую энергию, работу сил вредных сопротивлений и веса. Для режима выбега: wi = 0, Ад.с. = 0, Ап.с. = 0 тогда: Запасённая кинетическая энергия при выбеге тратится на преодоление работ сил вредных сопротивлений и веса. Режимы разгона и выбега называют режимами неустановившегося движения. 30. Установившийся режим движения машины. Коэффициент изменения средней скорости. Установившийся режим движения машины наступает тогда, когда работа внешних сил за цикл не изменяет ее энергии, то есть суммарная работа внешних сил за цикл движения равна нулю.  При установившемся движении уравнение энергетического баланса:  Где  соответственно работа за цикл движущих сил и сил сопротивления, ϕ10 - начальное значение обобщенной координаты, Δϕц - приращение обобщенной координаты за цикл. В пределах цикла текущее значение суммарной работы не равно нулю. Работа может быть то положительной, то отрицательной. При положительной величине работы машина увеличивает свою кинетическую энергию за счет увеличения скорости, то есть разгоняется. На участках, где суммарная работа отрицательна, кинетическая энергия и скорость машины уменьшается, машина притормаживается. В установившемся режиме величины увеличения скорости на участках разгона и снижения на участках торможения за цикл равны, поэтому средняя скорость движения w1ср постоянна. Коэффициент изменения средней скорости. Величина амплитуды колебаний скорости Δw1 определяется разностью между максимальной w1maxи минимальной w1minскоростями. За меру измерения колебаний скорости в установившемся режиме принята относительная величина, которая называется коэффициентом изменения средней скорости.  Где ω₁ср = (ω₁max + ω₁min) /2 – средняя угловая скорость машины. Для различных машин в зависимости от требований нормального функционирования (обрыв нитей в прядильных машинах, снижение чистоты поверхности в металлорежущих станках, нагрев обмоток и снижение КПД в электрогенераторах и т.д.) допускаются различные максимальные значения коэффициента изменения средней скорости. Существует нормативная документация, устанавливающая допустимые значения коэффициента неравномерности [δ]. Чтобы снизить внутреннюю виброактивность и неравномерность движения применяются различные методы: ⇒ уменьшение влияния неравномерности внешних сил (например, применение многоцилиндровых ДВС, насосов и компрессоров с рациональным сдвигом рабочих процессов в цилиндрах); ⇒ уменьшение влияния переменности приведенного момента инерции (тоже обеспечивается увеличением числа цилиндров в поршневых машинах, а так- же уменьшением масс и моментов инерции деталей, приведенный момент инерции которых зависит от обобщенной координаты); ⇒ установка на валах машины центробежных регуляторов или аккумуляторов кинетической энергии - маховиков; ⇒ активное регулирование скорости с использованием систем автоматического управления, включая и компьютерное управление. 31. Силы в кинематических парах плоских механизмов (без учета трения). Сила, как векторная величина характеризуется относительно звеньев механизма тремя параметрами: координатами точки приложения, величиной и направлением. Рассмотрим с этих позиций реакции в кинематических парах плоских механизмов. 1. Поступательная КП. В поступательной КП связи, наложенные на относи- тельное движение звеньев, запрещают относительное поступательное движение по оси y и относительное вращение. Заменяя эти связи реакциями, получим реакцию Fij и реактивный момент Mij.  При силовом расчете поступательной КП определяются: реактивный момент Mij, величина реакции Fij; известны: точка приложения силы –геометрический центр кинематической пары A1п. и направление – нормаль к контактирующим поверхностям звеньев. Число связей в КП Sпл = 2, подвижность звеньев в КП Wпл =1, число неизвестных при силовом расчете ns = 2. 2. Вращательная КП. Во вращательной КП связи, наложенные на относи- тельное движение звеньев, запрещают относительное поступательное движение по осям y и x. Заменяя эти связи реакциями, получим реакцию Fij. При силовом расчете вращательной КП определяются: направление реакции Fij; величина реакции Fij; известна: точка приложения силы – геометрический центр кинематической пары B1в .  Число связей в КП Sпл = 2, подвижность звеньев в КП Wпл =1, число неизвестных при силовом расчете ns = 2. 3. Высшая КП. В высшей паре связи, наложенные на относительное движение звеньев, запрещают движение в направлении нормали к контактирующим поверхностям (ось y). Заменяя эту связь реакцией, получим реакцию Fij. При силовом расчете в высшей КП определяются: величина реакции Fij; известны: точка приложения силы – точка контакта рабочих профилей кинематической пары С2вп; направление вектора силы – контактная нормаль к профилям.  Число связей в КП Sпл = 1, подвижность звеньев в КП Wпл =2, число неизвестных при силовом расчете ns = 1. 32. Силовой расчет типовых механизмов Постановка задачи силового расчета: для исследуемого механизма при известных кинематических характеристиках и внешних силах определить уравновешивающую силу или момент и реакции в кинематических парах механизма. Виды силового расчета: · статический – для механизмов, находящихся в покое или движущихся с малыми скоростями, когда инерционные силы пренебрежимо малы, или в случаях, когда неизвестны массы и моменты инерции звеньев механизма (на этапах, предшествующих эскизному проектированию); Уравнения статического равновесия:  где Fi - внешние силы, приложенные к механизму или его звеньям, Mi - внешние моменты сил, приложенные к механизму или его звеньям. · кинетостатический – для движущихся механизмов при известных массах и моментах инерции звеньев, когда пренебрежение инерционными силами приводит к существенным погрешностям;  где Fui -инерционные силы, приложенные к звеньям, Mui- моменты сил инерции, приложенные к звеньям. · кинетостатический с учетом трения – может быть проведен, когда определены характеристики трения в КП и размеры элементов пар. Определение числа неизвестных при силовом расчете. Для определения числа неизвестных, а, следовательно, и числа независимых уравнений, при силовых расчетах необходимо провести структурный анализ механизма и определить число и классы кинематических пар, число основных подвижностей механизма, число избыточных связей. Чтобы силовой расчет можно было провести, используя только уравнения кинетостатики, необходимо устранить в нем избыточные связи. В противном случае, к системе уравнений кинетостатики необходимо добавить уравнения деформации звеньев, необходимые для раскрытия статической неопределимости механизма. Уравновешивающая сила или момент должны действовать по каждой основной подвижности механизма. Поэтому суммарное число неизвестных в силовом расчете определяется суммой связей в КП механизма и его основных подвижностей  33. Кинетостатический силовой расчет типовых механизмов Различают два этапа кинетостатического расчёта: - Расчёт механизма без учёта потерь на трение в кинематических парах. - После конкретного конструирования узлов производится дополнительный расчёт потерь мощности в кинематических парах на преодоление трения. Итогом кинетостатического расчёта является определение движущей силы на ведущем звене, которая даёт возможность определить крутящий момент по формуле Полная мощность определяется по формуле: 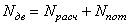 . По значению полной мощности выбирается мощность двигателя. . По значению полной мощности выбирается мощность двигателя.Порядок проведения кинетостатического расчёта: 1. Определение степени подвижности механизма. 2. Для каждого отдельного положения механизма внутри цикла его работы строятся планы скоростей и планы ускорений. С помощью планов ускорений определяются ускорения центров масс. 3. Механизм раскладывается на структурные группы Ассура. 4. Производится кинетостатический расчёт отдельных структурный групп начиная с последней, постепенно приближаясь к ведущему звену. 5. Кинетостатический расчёт ведущего звена. 6. Определение крутящего момента или движущей силы на ведущем звене. 7. Определение мощности двигателя. 8. Пункты 4-7 повторяются для множества положений механизма за полный цикл его работы. 9. Выбираются наибольшие значения мощности и усилий, действующие в кинематических парах. 10. На основании полученных данных составляется задание на проектирование. 34. Действие сил в поступательной паре с учетом трения. Сила трения на поверхности соприкосновения двух звеньев направлена в сторону, противоположную скорости относительного движения и приближённо может быть определена по формуле Кулона где Коэффициент трения зависит от многих факторов (чистоты поверхности, наличия и качества смазки, материала тел и др.) и определяется экспериментально. Сила трения покоя (сила сцепления), т.е. сила, которую надо преодолеть, чтобы тело привести в движение обычно больше силы трения скольжения, поэтому различают коэффициент сцепления Сила трения возникает как результат действия внешних силF, поэтому она является реактивной силой, в результате действия которой суммарная реакция 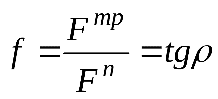 . Угол . Угол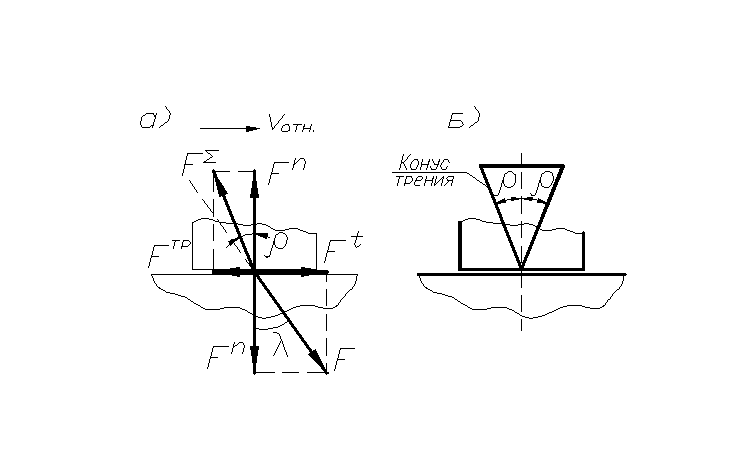 Если построить конус с углом при вершине 2·ρ (рис. 92, б), то получим конус трения. Движение возможно при т.е. при рис. 92 В общем случае движение возможно, если сила внешнего воздействия F находится за пределами конуса трения. Мощность, затрачиваемая на трение скольжения равна: где знак зависит от направления скоростей. 35. Трение во вращательных парах Вращательная кинематическая пара образуется цапфой (опорной частью вала) и охватывающим её подшипником. Для того чтобы цапфа, находящаяся под действием нескольких приложенных к ней сил, могла вращаться, необходимо, чтобы равнодействующая Р этих сил (рис. 16.10) создавала момент не меньший момента силы трения. 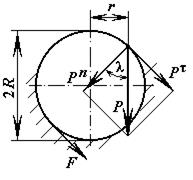 Рис. 16.10 Разложив силу Р на нормальную Рn и тангенциальную Рt составляющие и обозначив через: r плечо действия силы Р относительно оси вращения цапфы; R – радиус цапфы; l - угол между линией действия силы Р и радиусом, проведённым в точку приложения силы P, получим: момент, вращающий цапфу, равен  ; ;момент силы F трения равен Следовательно, момент силы Р не может вращать цапфы, если линия действия силы Р проходит внутри круга. Такой круг получил название – круга трения. 36.Механический коэффициент полезного действия η (КПД) – отношение работы сил производственных сопротивлений к работе всех движущих сил за время установившегося движения: η = Как видно из формулы (3.61), КПД показывает, какая доля механической энергии, приведенной к машине, полезно расходуется на совершение той работы, для которой машина создана. Отношение работы сил непроизводственных сопротивлений к работе движущих сил называется коэффициентом потерь: ψ =  . (3.62) . (3.62)Механический коэффициент потерь показывает, какая доля механической энергии, подведенной к машине, превращается в конечном счете в теплоту и бесполезно теряется в окружающем пространстве. Отсюда имеем связь между КПД и коэффициентом потерь η =1- ψ. Из этой формулы вытекает, что ни в одном механизме работа сил непроизводственных сопротивлений не может равняться нулю, поэтому КПД всегда меньше единице (η <1). Из этой же формулы следует, что КПД может равняться нулю, если Адв.с=АFтр. Движение, при котором Адв.с= АFтрназываетсяхолостым. КПД не может быть меньше нуля, т.к. для этого необходимо, чтобы Адв.с<АFтр. Явление, при котором механизм находится в покое и при этом удовлетворяется условие Адв.с<АFтр, называется явлением самоторможения механизма. Механизм, у которого η = 1, называется вечным двигателем. Таким образом, коэффициент полезного действия находится в пределах 0 £ η < 1. 37.Синтез рычажных механизмов. Синтез осуществляется в несколько этапов: • Структурный синтез (выбор структуры механизма); • Кинематический синтез (определение геометрических параметров кинематической схемы); • Динамический синтез (определение динамических параметров: масс, моментов инерции звеньев и др.). Структурный синтез может осуществляться по «структурным слоям»: если к стойке присоединять структурные группы, то всегда будет получаться нормальный механизм. Таких механизмов может быть множество. Для того, чтобы оценить качество проектируемого механизма, надо задаться критериями оценки (критериями синтеза) и их желательными абсолютными или относительными значениями. Входными параметрами синтеза являются критерии оценки механизма, а выходными – геометрические или динамические параметры кинематической схемы. Если число входных параметров соответствует числу выходных параметров, то задача синтеза может быть решена. Если имеется несоответствие между числом входных и выходных параметров синтеза, то задача либо не имеет решения в общем случае (число входных параметров больше), либо имеет множество решений (число входных параметров меньше числа выходных). В последнем случае часть выходных параметров задают произвольно, а остальные вычисляют, пользуясь составленными соотношениями между входными и выходными параметрами. При этом может получиться некоторое множество вариантов механизма с различной структурой, разным числом звеньев, разными габаритами, массой, энергопотреблением и т.д. Сравнивая варианты, выбирают такой, который в наилучшей степени соответствует выбранным критериям синтеза. 38 Условия существования кривошипа Важной кинематической характеристикой при синтезе механизма является проворачиваемость его звеньев, т.е. наличие в нем одного или двух кривошипов. Она зависит от соотношения длин звеньев. Рассмотрим плоский шарнирный четырехзвенник ABCD (рис. 10.1). Заданы l1, l2, l3 и l4 — длины звеньев, причем для исследования вариантов длин стойки принимают: l1 < l2 < l3 < l4. Для того, чтобы звено АВ было кривошипом, оно должно при вращении последовательно пройти через крайние левое (АВ1) и правое (АВ2) положения. На рис. 10.1 шарнирный четырехзвенник показан в двух крайних положениях совпадения кривошипа и стойки: штриховыми линиями — крайнее левое положение, штрихпунктирными — крайнее правое. Линиями видимого контура показано произвольное положение механизма. Из DВ1С1D следует:  из DВ2С2D: .  Рис. 10.1 Независимо от соотношения длин l2 и l3 неравенство всегда обеспечит выполнение другого неравенства. Позиции AB1 и AB2 характеризуют крайние положения звена 1, которое будет кривошипом, т.е. звеном, совершающим полный оборот. Позиции DC1 и DC2 свидетельствуют о том, что звено CD не совершает полного оборота. Оно совершает качательное движение и называется коромыслом. Механизм с данными свойствами называется кривошипно-коромысловым. Неравенство 2 характеризуется правилом Грасгофа, которое можно записать следующим образом. NB 10.2. Правило Грасгофа: Для существования кривошипа в шарнирном четырехзвеннике необходимо, чтобы сумма длин кривошипа и стойки была меньше суммы длин двух других звеньев. 39. Синтез кривошипно-коромыслового механизма по коэффициенту изменения средней скорости коромысла. Кривошипно-коромысловый механизм. Заданы длина коромысла l3, угол его размаха  Схема синтеза кривошипно-коромыслового механизма Определяем угол между крайними положениями шатуна АВ:  . .Из середины отрезка B1B2 точки Е проводим прямую через центр качания коромысла (точка О2). Строим  ). Из точки F радиусом ). Из точки F радиусом Длина кривошипа O1A  ; ;Длина шатуна AB 40. Манипуляторы. Манипулятор – совокупность пространственного рычажного механизма и системы приводов, осуществляющая под управлением программируемого автоматического устройства или человека-оператора действия (манипуляции), аналогичные действиям руки человека. Устройство и применение манипуляторов Основу манипуляторов составляют пространственные механизмы со многими степенями свободы. Манипуляторы выполняют работы в средах, недоступных или опасных для человека (подводные глубины, вакуум, радиоактивная среда и другие агрессивные среды), вспомогательные работы в промышленном производстве. Манипуляторы используются в медицинской технике (например, в протезировании). Манипуляторы изучает теория манипуляторов, которая является разделом теории машин и механизмов. В узком смысле манипулятором называется механическая рука. Манипуляторы делятся на управляемые человеком и автоматические манипуляторы (роботы-манипуляторы как разновидность роботов). Развитие манипуляторов привело к созданию промышленных роботов. Проектирование механизмов-манипуляторов требует решения таких задач, как создание манёвренности, устойчивости в работе, выбор правильного соотношения полезных и холостых ходов. Иногда требуется проектирование таких систем, в которых оператор чувствует усилие, создаваемое на рабочем органе или на грузозахвате. 41 Технические показатели кинематической схемы манипуляторов промышленных роботов. Манипулятор – управляемое устройство или машина для выполнения двигательных функций, аналогичных функциям руки человека при перемещении объектов в пространстве, оснащенное рабочим органом.  Оптимальная система расположения элементов кинематической пары - понятие относительное: конструкция оптимальная для одних условий, может быть неприемлемой для других. Часто это связано с технологичностью, как совокупностью свойств конструкции, проявляемых при оптимальных затратах труда, средств, материалов и времени при принятых условиях изготовления, эксплуатации и ремонта промышленного робота. Конструкция, достаточно технологичная в единичном производстве, часто оказывается малотехнологичной в массовом производстве и совершенно нетехнологичной в автоматизированном производстве. Основные технические показатели промышленных роботов: Грузоподъемность руки ПР , Число степеней подвижности ПР - сумма возможных координатных движений объекта манипулирования относительно опорной системы (стойки, основания) ПР. Погрешность позиционирования - отклонение заданной позиции исполнительного механизма от фактической при многократном позиционировании (повторении движения). Погрешность позиционирования может оцениваться в линейных или угловых единицах. Погрешность отработки траектории рабочего органа ПР - отклонение фактической траектории от заданной по программе. Рабочее пространство промышленного робота (манипулятора или автооператора) - пространство, в котором может находиться исполнительный орган (устройство) ПР, М или А. Рабочая зона ПР, М или А - пространство, в котором может находиться рабочий орган (например, рука) при функционировании ПР, М или А. Зона обслуживания ПР, М или А - часть рабочей зоны, где полностью сохраняются заданные (паспортные) значения технических характеристик ПР, М или А. Мобильность ПР определяется его возможностью совершать движения. По мобильности роботы подразделяют на две группы: стационарные (обеспечивающие ориентирующие и транспортирующие движения) и передвижные (обеспечивающие дополнительно к названным еще и координатные движения). 42. Статическое уравновешивание механизма. Распределение масс звеньев механизма, переводящее его центр масс в неподвижную точку, называется статическим уравновешиванием. При движении звеньев механизма в кинематических парах возникают дополнительные динамические нагрузки от сил инерции звеньев. Это возникает из-за того, что центры масс звеньев в общем случае имеют переменные по величине и направлению ускорения. Т.к. всякий механизм имеет неподвижное звено-стойку, то и на стойку механизма также воздействуют вполне определенные динамические нагрузки. В свою очередь через стойку эти нагрузки передаются на фундамент механизма. Динамические нагрузки, возникающие при движении механизма, являются источниками дополнительных сил трения в кинематических парах, вибраций звеньев и фундамента, дополнительных напряжений в отдельных звеньях механизма, причиной шума и т.д. Поэтому при проектировании механизма ставится задача о рациональном подборе масс звеньев механизма, обеспечивающем полное или частичное устранение указанных динамических нагрузок. Решение подобной задачи, относящейся к динамическому проектированию механизма машины, называется его уравновешиванием. Цель уравновешивания механизмов – устранение переменных воздействий на фундамент, вызывающих кинематические колебания, как самого фундамента, так и здания, в котором он находится. Наиболее просто и наглядно статическое уравновешива ние выполняется методом заменяющих масс. Пусть дано движущееся звено массой т с центром масс S(рис. а).  Сосредоточим массу звена, распределенную по всему его объему, в точках А и В (рис. б). Величины сосредоточен ных масс найдутся из уравнений:  откуда   При этом масса звена и положение его центра масс не из менились. 43. Метод замещающих масс. Применяется для уравновешивания механизмов. При использовании этого метода, звено механизма с распределенной массой заменяется расчетной моделью, которая состоит из точечных масс.  Условия перехода от звена с распределенной массой к модели с точечными массами: 1. Сохранение массы звена: 2. Сохранение положения центра масс: 3. Сохранение момента инерции 44. Условия существования зубчатой передачи. Зубчатыми передачами называются механизмы с высшими кинематическими парами в состав которых входят зубчатые колеса, рейки или секторы - звенья, снабженные профилироваными выступами или зубьями. Условием существования высшей кинематической пары является условие неразрывности контакта звеньев, которое заключается в том, что проекции скоростей звеньев в точке контакта на контактную нормаль к профилям должны быть равны. При выполнении этого условия профили не отстают друг от друга (нарушение контакта приведет к исчезновению пары), и не внедряются друг в друга. 45. Основная теорема плоского зацепления. Основная теорема плоского зацепления сформулирована Виллисом (Теорема Виллиса). Передаточное отношение между звеньями, совершающими вращательное движение, прямопропорционально отношению угловых скоростей и обратно пропорционально отношению расстояний от центров вращения до полюса. В ней подчеркивается, что для обеспечения заданного передаточного отношения необходимо и достаточно, чтобы нормаль к профилям зубьев в контактных точках (контактная нормаль) пересекала бы в процессе зацепления профилей линию межосевого расстояния передачи все время в одной и той же точке. В эвольвентном зацеплении контактной нормалью является линия зацепления N1N2, а точкой линии межосевого расстояния, через которую она проходит при зацеплении зубьев полюс зацепления П передачи. Следует отметить, что теорема зацепления удовлетворяется и в том случае, если профиль зубьев одного из колес выбран произвольно, а профиль зубьев парного колеса построен как сопряженный выбранному. Следствия из теоремы Виллиса: 1.Точка профиля зуба работает только тогда, когда нормаль к профилю в ней проходит через полюс зацепления П. Обе нормали в точке Т касания профилей сливаются в одну и проходят через полюс П. 2.Нормали к профилю в его рабочей части должны пересекать начальную окружность зубчатого колеса. 3.Точки рабочего профиля работают в том порядке, в каком нормали в них проходят через полюс зацепления П. 4.Рабочие профили проскальзывают при зацеплении. Скорость скольжения профилей (внешнее зацепление): V12 = (ω1 + ω2) ПТ 46.Скорость скольжения профиля. Скорость скольжения профилей в высшей кинематической паре равна произведению скорости относительного вращения на расстояние от контактной точки до полюса зацепления:  Для внутреннего зацепления Для внутреннего зацепления  В полюсе зацепления lKP = 0 и следовательно скорость скольжения равна нулю Vck = 0 , т.е. профили перекатываются без скольжения.В случае цилиндрических передач рассматривают: а) Внешнее зацепление  б) Внутреннее зацепление  Vp= Vp1 = Vp2 в) Зацепление реечное Vp2 = Vp1 =  1 1  rw1 rw1Ввиду ограниченности объема курса предметом дальнейшего изучения будут прямозубые и эвольвентные косозубые зубчатые передачи, у которых u = const. Геометрию таких колёс передачи определяют эвольвента окружности. 47.Угол давления определяет положение нормали в высшей КП относительно вектора скорости и контактной точки ведомого звена. Его величина определяется размерами механизма, передаточной функцией и перемещения толкателя S. Угол передачи движения γ - угол между векторами абсолютной и относительной (по отношению к кулачку) скоростей той точки толкателя, которая находится в точке контакта. Если пренебречь силой трения между кулачком и толкателем, то силой, приводящей в движение толкатель (движущей силой), является давление Q кулачка, приложенное к толкателю в точке А и направленное по общей нормали к профилям кулачка и толкателя. Разложим силу Q на взаимно перпендикулярные составляющие Q1 и Q2, из которых первая направлена по направлению скорости. Сила Q1 перемещает толкатель, преодолевая при этом все полезные (связанные с выполнением технологических задач) и вредные (силы трения) сопротивления, приложенные к толкателю. Сила Q2 увеличивает силы трения в кинематической паре, образованной толкателем и стойкой. Очевидно, что с уменьшением угла γ сила Q1 уменьшается, а сила Q2 увеличивается. При некотором значении угла γ может оказаться, что сила Q1 не сможет преодолеть все сопротивления, приложенные к толкателю, и механизм не будет работать. Такое явление называют заклиниванием механизма, а угол γ , при котором оно имеет место, называют углом заклинивания. При проектировании кулачкового механизма задают допускаемое значение угла давления, обеспечивающее выполнения условия γ ≥ γ min > γ закл, т. е. текущий угол γ ни в одном положении кулачкового механизма не должен быть меньше минимального угла передачи γ min и значительно превосходить угол заклинивания γзакл . Для кулачковых механизмов с поступательно движущимся толкателем рекомендуется γ min = 60° и γmin = 45° - механизмов с вращающимся толкателем. 48. Производящие поверхности. Станочное зацепление Геометрия зубчатого колеса зависит в первую очередь от размеров и формы инструмента. Поэтому стандартизация параметров инструмента, воспроизводящего эвольвентный профиль зубчатого колеса, необходима с технической и экономической точек зрения. За основу стандарта форм и размеров зубчатого колеса принят теоретический исходный контур (ТИК, рис. 20.4),который представляет собой чередующиеся симметричные зубья и впадины трапециевидной формы. Размеры теоретического исходного контура установлены государственным стандартом. Базовая линия теоретического исходного контура, по которой толщина зуба равна ширине впадины, называется его делительной прямой. Расстояние между одноименными профилями соседних зубьев по делительной или по любой другой параллельной ей прямой называют шагом зубьев р исходного контура.  Если форма инструмента повторяет форму ТИК, а делительная прямая является начальной прямой, то начальная окружность нарезаемого колеса касается делительной прямой ТИК. Как уже отмечалось ранее, подвижные центроиды катятся друг по другу без скольжения, поэтому шаг зубьев по начальной окружности колеса должен быть равен шагу зубьев ТИК. Если z – число зубьев нарезаемого колеса, то длина окружности – подвижной центроиды колеса равна: πd=zp где d – диаметр подвижной центроиды колеса: d = pz/π = mz. Подвижную центроиду колеса, при его зацеплении с рейкой, называют делительной окружностью. Делительная окружность делит зуб на делительную головку и делительную ножку. В выражении (20.4) введён основной параметр зубчатого зацепления – модуль m: m = p/π (20.5) модуль измеряется в мм и может принимать только значения оговоренные ГОСТом. В долях модуля задаются все линейные размеры контура: высота делительной головки: ha = ha*m (20.6) высота делительной ножки: hf = (ha*+c)m (20.7) радиус переходной кривой: ρf = ρf*m (20.8) где ha* - коэффициент высоты головки с* - коэффициент радиального зазора ρf* - коэффициент радиуса переходной кривой. |
