1. Цель и задачи курса теории механизмов и машин. Теория механизмов и машин

• Название: 1. Цель и задачи курса теории механизмов и машин. Теория механизмов и машин
• Дата: 09.03.2018
• Размер: 0.77 Mb.
• Имя файла: TMM.docx
• Тип: Документы; #38026
• страница: 5 из 5

52. Основные параметры эвольвентных цилиндрических передач

В качестве главного профиля зубьев цилиндрических зубчатых колес, наибольшее распространение получил эвольвентный профиль. Плоская эвольвента окружности представляет собой траекторию любой точки прямой линии, перекатываемой без скольжения по эволюте, т.е. по основной окружности радиуса r_b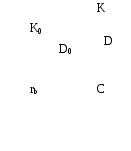



Перекатываемая по основной окружности прямая называется производящей прямой. Свойства эвольвенты окружности.

1. 
   Нормаль к эвольвентам (прямая КС) касается основной окружности, точка касания (С) - центр кривизны эвольвент.
   
2. 
   Все эвольвенты одной основной окружности эквидистантны, и расстояние KD между ними равно длине дуги К₀D₀.
   
3. 
   Каждая ветвь эвольвенты вполне определяется радиусам основной окружности и положением начала отсчета эвольвентного угла.
   
4. 
   Эвольвента не имеет точек внутри основной окружности.
   

Уравнение эвольвенты -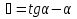

Каждая ветвь эвольвенты определяется радиусом основной окружности

Теоретический и производящий исходные контуры

За основу стандарта форм и размеров зубчатого колеса принят теоретический исходный контур ТИК, который представляет собой чередующиеся симметричные зубья и впадины трапециевидной формы. Базовая линия теоретического исходного контура, по которой толщина зуба равна ширине впадины, называется его делительной прямой. Расстояние между одноименными профилями соседних зубьев по делительной или по любой другой параллельной ей прямой называют шагом зубьев р исходного контура.




. Если z – число зубьев нарезаемого колеса, то длина окружности – подвижной центроиды колеса равна: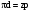

где d – диаметр подвижной центроиды колеса: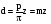

Подвижную центроиду колеса при его зацеплении с рейкой называют делительной окружностью. Делительная окружность делит зуб на делительную головку и делительную ножку.

модуль m: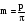

53 Волновые зубчатые передачи

Волновая зубчатая передача — механизм, содержащий зацепляющиеся между собой гибкое и жесткое зубчатые колеса и обеспечивающий преобразование и передачу движения благодаря деформированию гибкого колеса (рис. 19.1).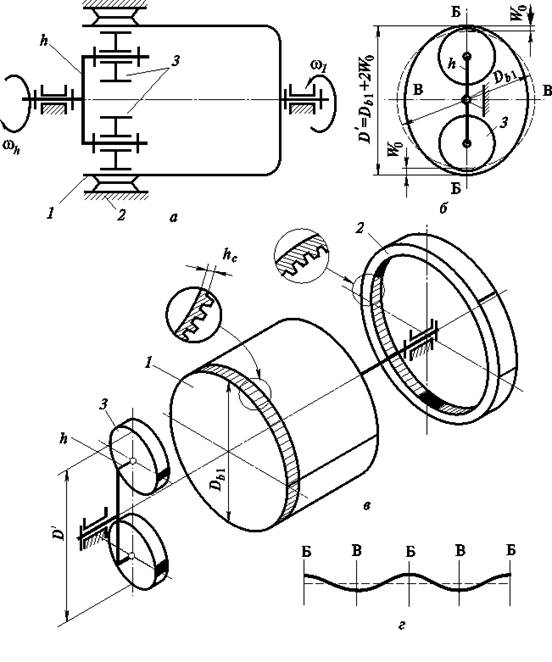



Рис. 19.1

Волновая зубчатая передача (ВЗП) состоит из трех основных элементов: гибкого колеса 1 (рис. 19.1, а, б, в), жесткого колеса 2 и генератора волн h. Ее можно рассматривать как конструктивную разновидность планетарной передачи с внутренним зацеплением, характерной особенностью которой является использование сателлита (гибкого колеса), деформируемого в процессе передачи движения. Для обеспечения симметрии нагружения волновой зубчатой передачи используют две волны деформации и четные числа зубьев колес, которые связаны соотношением  .

Кинематика волновой передачи. При вращении генератора волн обе волны деформации перемещаются по периметру гибкого колеса. В результате каждый зуб гибкого колеса за один оборот генератора волн дважды входит в зацепление с зубьями жесткого колеса.

Волновая передача может быть двухступенчатой. В этом случае гибкое колесо 1 выполняется в виде кольца с двумя зубчатыми венцами  и  , которые входят в зацепление с жесткими колесами , имеющими соответственно  и  зубьев. Если жесткое колесо 2 неподвижно, то движение от вала генератора волн преобразуется с помощью двух волновых зацеплений и передается на выходной вал, соединенный с жестким колесом 

Передаточное отношение двухступенчатой ВЗП определяется формулой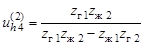

 

Особенности волнового зацепления. Гибкое колесо ВЗП при его нагружении изменяет свою начальную форму. Это происходит из-за наличия зазоров и упругости элементов, взаимодействующих с гибким колесом. Изменение формы гибкого колеса  ограничено с внешней стороны жестким колесом , а с внутренней генератором волн h. Гибкое колесо, опирающееся на генератор волн в пределах участков постоянной кривизны   стремится принять форму жесткого колеса. С увеличением момента закручивающего гибкое колесо зоны выбранных зазоров в зацеплении увеличиваются, что приводит к увеличению числа пар зубьев в зацеплении. Благодаря многопарности зацепления нагрузочная способность ВЗП выше, чем планетарной. КПД волновой передачи также выше, потому что в зацеплении зубья почти не перемещаются при прилегании гибкого колеса к жесткому. При стальных гибких колесах в одноступенчатых волновых передачах можно получить передаточное отношение 60 – 320, а КПД равным 0,85...0,80. Двухступенчатые ВЗП обеспечивают передаточные отношения от  до  и более при КПД от 0,7 до 0,1.

с. 19.3

54 Червячные зубчатые передачи.

Червячной - называется зубчатая передача, состоящая из двух подвижных звеньев - червяка и зубчатого колеса и предназначенная для передачи и преобразования вращательного движения между ортагональными перекрещивающимися осями. Червяком называют звено, наружная поверхность которого имеет форму винта. Червячным колесом называется зубчатое колесо с косыми зубьями, которое зацепляется с червяком

Виды червячных передач и червяков:

1. 
   по виду делительной поверхности червяка
   
   • 
     цилиндрические червячные передачи
     
   • 
     глобоидные червячные передачи
     
2. 
   по виду теоретического торцового профиля витка червяка
   
   • 
     архимедов червяк (ZA) - профиль выполнен по архимедовой спирали;
     
   • 
     эвольвентный червяк (ZI) - профиль выполнен по эвольвенте окружности;
     
   • 
     конволютный червяк (ZN) - профиль выполнен по удлиненной эвольвенте
     

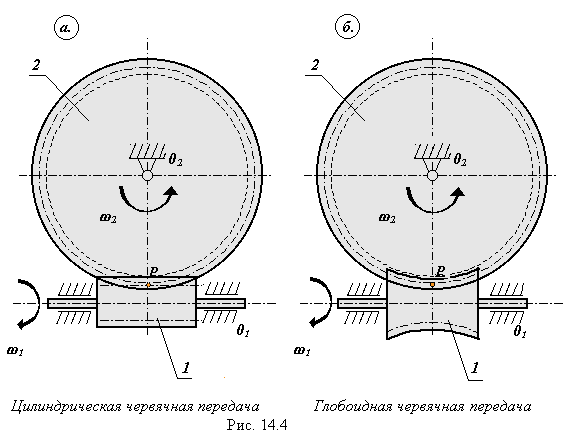Геометрия зацепления цилиндрической червячной передачи

Связь между основными параметрами червяка - диаметром начального цилиндра d w1 , ходом винтовой линии pz1 и углом ее наклона bw - устанавливается следующим соотношением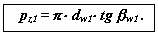



Связь между ходом винтовой линии pz1 и шагом многозаходного винта p1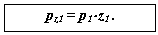



55.Планетарная зубчатая передача.

Планетарной зубчатой передачей называют механизм для передачи и преобразования вращательного движения, содержащий зубчатые колеса с перемещающейся осью вращения хотя бы одного из них. Конструктивно ПП всегда представляет собой набор взаимозацепленных зубчатых колёс  часть из которых имеет общую геометрическую неподвижную ось вращения, а другая часть имеет подвижные оси вращения, концентрически вращающиеся на так называемом «водиле» вокруг неподвижной. Зубчатые колёса на неподвижной оси всегда связаны друг с другом не напрямую, а через зубчатые колёса на подвижных осях, а ввиду того, что вторые способны не только вращаться относительно первых, но и обкатывать их, тем самым передавая поступательное движение на водило, все звенья. Конструкция передачи со многими сателлитами обеспечивает зацепление большего числа зубцов и потому меньшую нагрузку на каждый зубец. Это позволяет достичь меньших размеров и массы по сравнению с обычной передачей при той же передаваемой мощности.

Соосность ведущих и ведомых валов облегчает компоновку машин и каскадных механизмов.

Сбалансированность сил в передаче приводит к меньшему уровню шума.

Конструкция передачи позволяет достичь больших передаточных отношений при малом числе колёс.

К недостаткам планетарных передач относят повышенные требования к точности изготовления и сборки, а также малый КПД при больших передаточных отношениях.

56,Передаточное отношение планетарных передач.

Передаточное число зубчатой передачи – это отношение числа зубьев ведомого зубчатого колеса к числу зубьев ведущего колеса.

При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, а два других служат в качестве ведущего и ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также от того, какой элемент закреплён.

ередаточное отношение 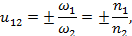 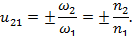(иногда используется обозначение ) определяется при ведущем колесе 1, передаточное отношение  определяется если ведущим является колесо 2:




 

Передаточное число зубчатой передачи – это отношение числа зубьев ведомого зубчатого колеса к числу зубьев ведущего колеса. Передаточное число зубчатой передачи определяется по формуле: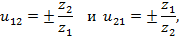



Передаточное число планетарного механизма определяется по формуле:



где 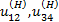- передаточные числа ступеней (с учетом знаков) при остановленном водиле.

57. Метрический синтез планетарных механизмов.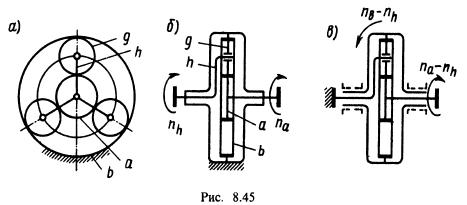


Кинематика. При исследовании кинематики планетарных передач широко используют метод остановки водила — метод Виллиса. Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм (рис. 8.45, б), представляющий собой простую передачу, в которой движение передается οт α к ί через паразитные колеса g. Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила. В качестве примера проанализируем кинематику передачи, изображенной на рис. 8.45. Условимся приписывать частотам вращения индекс звена (а, n_h и т. д.), а передаточные отношения сопровождать индексами в направлении движения и индексом неподвижного звена. Например, i^h_ba означает передаточное отношение от А к А при неподвижном Ь. Для обращенного механизма



В планетарных передачах существенное значение имеет знак передаточного отношения. Условимся, что при />0 вращение ведущего и ведомого звеньев происходит в одном направлении; при /<0 вращение противоположное. В рассматриваемом примере колеса а и b вращаются в разных направлениях, а потому i^h_ab<0. Переходя к реальному механизму, у которого в большинстве случаев практики колесо b заторможено, а — ведущее и h — ведомое, на основе формулы (8.74) при n = 0 получаем



Частоту вращения сателлита определим из равенства



При заданных n_а и n_h определяют n_д или (n_g — n_h) как частоту вращения сателлита относительно водила или относительно своей оси (используют при расчете подшипников). Далее,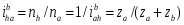



Для случая, когда неподвижно колесо я, на основе формулы (8.74) при n_в = 0 с помощью аналогичных преобразований находим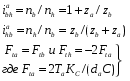



Анализ кинематики планетарных передач, выполненных по другим схемам, производят таким же методом.
58.кулачковые механизмы.

Кулачковым называется механизм, который содержит два основных звена: кулачок и толкатель, образующих высшую кинематическую пару.

Достоинства кулачковых механизмов: 1) возможность воспроизведения практически любого закона движения выходного звена; 2) малое количество деталей (кулачок и толкатель), что позволяет просто изготавливать и обслуживать.

Недостаток: наличие высшей кинематической пары, в которой могут возникать повышенные удельные давления, что может привести к разрушению поверхности кулачка.

Кулачок — звено, входящее в высшую кинематическую пару, рабочая поверхность которого имеет переменную кривизну. Простейший кулачковый механизм состоит из кулачка, толкателя и стойки. Выбором профиля кулачка можно получить практически любой закон движения выходного звена. Кулачковые механизмы классифицируются по следующим признакам:

1. По расположению звеньев в пространстве

♦ пространственные;

♦ плоские;

2. По движению кулачка

♦ вращательное;

♦ поступательное;

♦ винтовое;

3. По движению выходного звена

♦ возвратно-поступательное (с толкателем);

♦ возвратно-вращательное (с коромыслом);

4. по наличию ролика

♦ с роликом;

♦ без ролика;

5. По виду кулачка

♦ дисковый (плоский);

♦ цилиндрический;
♦ коноид (сложный пространственный);

6. По форме рабочей поверхности выходного звена ♦ плоская;

♦ заостренная;

♦ цилиндрическая;

♦ сферическая;

♦ эвольвентная;

7. По способу замыкания элементов высшей пары

♦ силовое;

♦ геометрическое.

При силовом замыкании удаление толкателя осуществляется воздействием контактной поверхности кулачка на толкатель (ведущее звено – кулачок, ведомое – толкатель). Движение толкателя при сближении осуществляется за счет силы упругости пружины или силы веса толкателя, при этом кулачок не является ведущим звеном. При геометрическом замыкании движение толкателя при удалении осуществляется воздействием наружной рабочей поверхности кулачка на толкатель, при сближении – воздействием внутренней рабочей поверхности кулачка на толкатель. На обеих фазах движения кулачок ведущее звено, толкатель – ведомое.
59. Кинематика кулачковой передачи.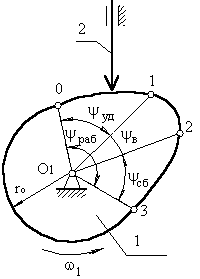


В процессе работы толкатель совершает в соответствии с рисунком 3 движения:

1) поступательно вверх – в этом случае толкатель взаимодействует с участком 01;

2) стоит на месте (выстой) – контакт с участком 12. Здесь постоянный радиус кривизны.

3) толкатель опускается (сближение) – контакт с участком 23.

В первой фазе подъему толкателя (фаза удаления) на профиле кулачка соответствует угол ψ_удал; в фазе выстоя – ψ_выс; в фазе сближения – ψ_сб.ψ_удал + ψ_выс + ψ_сб = ψ_раб – рабочий угол профиля кулачка.

Угол профиля кулачка можно показать только на кулачке.

Угол поворота кулачка, соответствующий выше указанным фазам перемещения толкателя, определяют, используя метод обращения

движения, в соответствии с которым всей системе, включая стойку, мысленно сообщают движение с угловой скоростью (ω₁).Тогда в обращенном движении кулачек становится неподвижным: ω*₁ = ω₁ + (–ω₁) = 0,

а ось толкателя вместе со стойкой будут перемещаться в направлении (–ω₁). И угол поворота кулачка, соответствующий той или иной фазе движения, определяется по углу поворота оси толкателя в обращенном движении на соответствующем участке. Ось толкателя в обращенном движении в любом положении будет касаться окружности радиуса r_е.

Поворот кулачка на участке: 01 – φ_01, 12 – φ_{12 ,} 23 – φ₂₃

рабочий угол поворота кулачка φ_раб: φ_раб = φ₀₁ + φ₁₂ + φ₂₃

Всегда независимо от схемы механизма φ_раб = ψ_раб, а

φ_уд ≠ ψ_уд, φ_выс ≠ ψ_выс, φ_сб ≠ ψ_сб, для всех схем, кроме кулачкового механизма с центральным толкателем.

61. Динамика кулачковой передачи.

Динамика - раздел механики машин и механизмов, изучающий закономерности движения звеньев механизма под действием приложенных к ним сил.
В основе динамики лежат три закона, сформулированные Ньютоном, из которых следует: 
Из первого закона: Если равнодействующая всех внешних сил, действующих на механическую систему равно нулю, то система находится в состоянии покоя. 
Из второго закона: Изменение состояния движения механической системы может быть вызвано либо изменением действующих на нее внешних сил, либо изменением ее массы. 
Из этих же законов следует, что динамическими параметрами механической системы являются:

• 
  инерциальные (массы m и моменты инерцииI);
  
• 
  силовые (силы F_ij и моменты сил M_ij);
  
• 
  кинематические (линейные a и угловые e ускорения).
  

60. Силы в кулачковой передаче

Сила, действующая на толкатель со стороны кулачка и вызывающая его движение, направлена по нормали к кулачку в точке контакта его с толкателем. Поэтому в общем случае она направлена под углом к направлению движения толкателя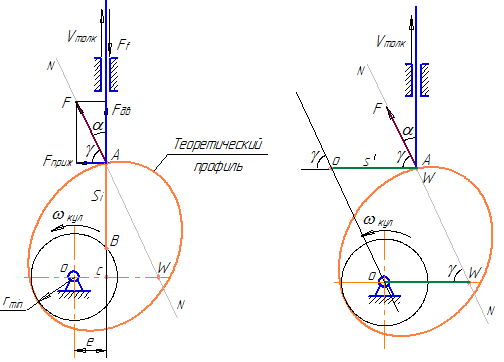


Угол между действующей на толкатель силой и направлением его движения называется углом давления(обозначается α), а угол между действующей силой и направлением, перпендикулярным направлению движения толкателя называется углом передачи движения (обозначается γ). В сумме эти углы составляют угол, равный 90⁰, поэтому при рассмотрении работоспособности механизма с учетом направления передачи сил можно оперировать любым из них.

Сила давления кулачка на толкатель F (без учета сил трения) направлена по нормали к профилю кулачка.

Под действием движущей силы F cos толкатель поднимается и преодолевает силы полезных сопротивлений и силы трения в направляющих толкателя.

Сила вызывает перекос толкателя и возникновение сил трения в направляющих толкателя. Если эта сила велика, то может произойти заклинивание и поломка толкателя.

62. Метрический синтез кулачковой передачи.

 На этом этапе определяются основные размеры звеньев механизма, которые обеспечивают заданный закон преобразования движения в механизме или заданную передаточную функцию. Как отмечалось выше, передаточная функция является чисто геометрической характеристикой механизма, а, следовательно, задача метрического синтеза чисто геометрическая задача, независящая от времени или скоростей. Основные критерии, которыми руководствуется проектировщик, при решении задач метрического синтеза: минимизация габаритов, а, следовательно, и массы; минимизация угла давления в вышей паре; получение технологичной формы профиля кулачка.