9. Неравномерность движения машины. Различные периоды и режимы движения машины

• Название: 9. Неравномерность движения машины. Различные периоды и режимы движения машины
• Дата: 04.03.2019
• Размер: 222.75 Kb.
• Имя файла: 9-12.docx
• Тип: Документы; #69503

9. Неравномерность движения машины. Различные периоды и режимы движения машины.

циклически повторяющееся изменения угловой скорости кривошипа характерны для многих машин: строгальных, долбежных, ткацких станков, кривошипных прессов, многих станков-автоматов, компрессоров, насосов-качалок и т.п. При этом в большинстве машин период изменения угловой скорости равен времени одного оборота кривошипа.

Причин циклической неравномерности вращения кривошипа две:

первая причина – непостоянство внешних сил, действующих на звеньях механизма (точнее - несовпадение по времени работ, поступающих с двигателя и расходуемых машин). Примером машины, где эта причина проявляет себя, служит тихоходный поршневой насос. В нем на такте выталкивания жидкости на поршень действует значительное усилие; оно заставляет кривошип уменьшить его угловую скорость к концу этого такта. На такте всасывания усилие на поршень невелико и двигатель к концу всасывания «разгонит» кривошип (таблица 2.1);

вторая причина – силы инерции, возникающие в звеньях при их движении (можно эту причину объяснить и иному: из-за изменения скоростей движения звеньев – ползуна, коромысла и т.п. – меняется их кинетическая энергия). Примерами машин, где эта причина проявляет себя, являются быстроходные автоматы, применяемые в легкой промышленности: силы инерции, возникающие из-за быстрого возвратно-поступательного движения звеньев, часто в несколько раз превосходят силы, действующие на рабочие органы (таблица 2.1).

Какая из двух причин неравномерности вращения кривошипа сказывается сильнее, зависит от соотношения рабочей нагрузки и сил инерции, действующих на звенья.

Степень циклической неравномерности вращения кривошипа характеризуют отношением: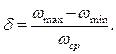

 , (2.3)

называемым коэффициентом неравномерности движения. Т.е., коэффициент неравномерности движения механизма δ – это отношение разности между максимальной и минимальной угловой скорости к её среднему значению.

Бόльшие значения δ нежелательны по ряду причин:

Во-первых, большие колебания скорости могут ухудшить рабочий процесс: в полиграфических машинах (могут смазывать изображение); в текстильных машинах (могут обрывать нить) и т.п.

Во-вторых, при увеличении δ возрастают динамические нагрузки в приводе от двигателя к рабочему органу и увеличиваются опасные резонансные колебания в валах.

В-третьих, асинхронные электродвигатели, приводящие в движение большинство машин, не допускают, чтобы колебания их угловой скорости превосходили 3-5 %, т.к. при δ = 0,03-0,05 их КПД уменьшается, обмотки перегреваются, что может привести к короткому замыканию.

Для изучения периодических колебаний скоростей во время установившегося движения необходимо знать среднюю скорость механизма. Т.к. скорость меняется от минимального значения до максимального, то средняя скорость будет равна средней арифметической

 . (2.4)

Физический смысл коэффициента неравномерности δ. Коэффициент неравномерности движения характеризует только перепад угловой скорости ведущего звена в пределах от ω_min до ω_max, но не показывает динамику движения внутри одного полного цикла периода установившегося движения, т.е. не зависит от частоты колебаний.

На рисунке 2.2 показаны два графика зависимости ω = ω(φ), у которых ω_max и ω_min равны, но угловые ускорения для графика (рисунок 2.2, б) значительно больше. Поэтому и динамические характеристики различны, т.е. различны кинетическая энергия, момент инерции и др.



а - с плавным изменением угловой скорости; б - менее плавным

Рисунок 2.2 - Графики зависимости угловой скорости

от угла поворота

Основные режимы движения машины.

Процесс движения машины в общем случае состоит из трех фаз: разбега, установившегося режима и выбега (рис. 7.2). Разбег (режимI и II) и выбег (режимы IV и V) относятся к неустановившемуся режиму, который характеризуется непериодическими, т. е. неповторяющимися, изменениями скорости главного вала машины (начального звена). Такой процесс движения называют переходным.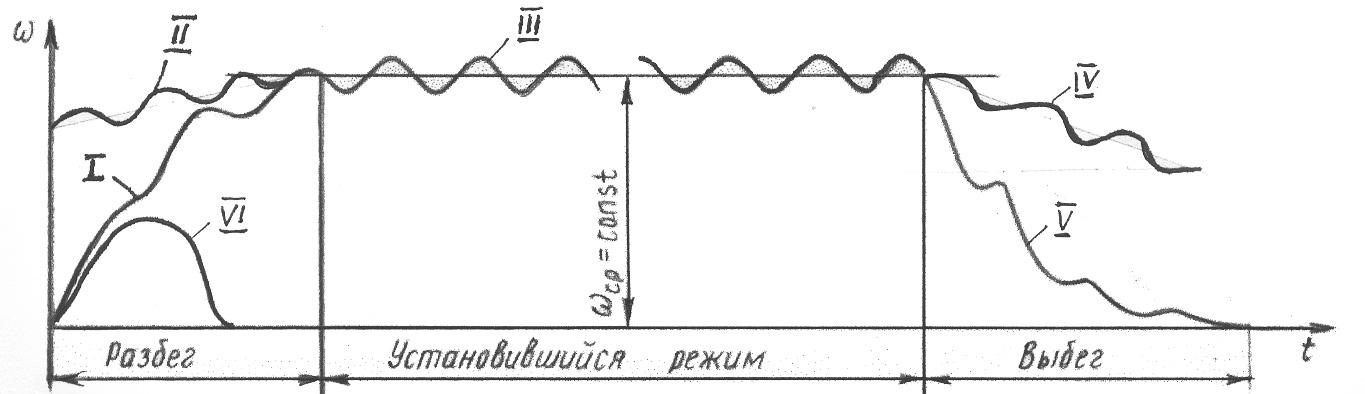

Рис. 7.2

При установившемся режиме III скорость главного вала изменяется периодически. В частном случае скорость может быть постоянной. В установившемся режиме работает большинство энергетических и технологических машин. Часто установившееся движение чередуется с разгонами (при повышениях скоростного режима II) и торможениями (при понижениях скоростного режима IV). Так работают, например, автомобильный двигатель и различные другие транспортные машины. Многие механизмы в установившемся режиме вообще не работают. Это особенно характерно для целого ряда приборов (реле, контакторы и т. п.). Их механизм во время срабатывания (режим VI) переходит из одного положения в другое, не совершая замкнутого повторяющегося кинематического цикла.

Неустановившийся режим движения машины имеет место тогда, когда ее пускают в ход и она, набирая скорость, выходит на установившийся режим, а также тогда, когда для остановки машины ее двигатель выключают и она продолжает двигаться за счет накопленного запаса кинетической энергии; при этом машина постепенно теряет скорость из-за действия сил трения или каких-либо других сил сопротивления, в том числе и специальных тормозных сил.

Разгоны (разбеги) и торможения могут происходить с большим ускорением. Это вызывает значительное динамическое нагружение механизма, что, в свою очередь, может привести к перенапряжениям и даже к поломкам.

Во время разбега и выбега угловая скорость многих машин проходит через критическую (резонансную) зону. Во избежание динамической перегрузки механизма и возможной аварии проход этой зоны должен быть достаточно быстрым, что надо обеспечить при проектировании, сделав расчет обеих фаз неустановившегося режима. Решение многих других динамических задач также связано с исследованием этого режима.

10. регулирование движения машин. Общие положения

Неравномерность движения и методы ее регулирования.

Уравнение работ является основным энергетическим уравнением установившегося режима. Из него вытекает, что приращения кинетической энергии механизма за цикл не происходит и, следовательно, угловая скорость начального звена в начале и в конце цикла одинакова, однако в пределах цикла текущее значение суммарной работы не равно нулю. Работа может быть то положительной, то отрицательной. При положительной величине работы машина увеличивает свою кинетическую энергию за счет увеличения скорости, то есть разгоняется. На участках, где суммарная работа отрицательна, кинетическая энергия и скорость машины уменьшается, машина притормаживается. В установившемся режиме величины увеличения скорости на участках разгона и снижения на участках торможения за цикл равны, поэтому средняя скорость движения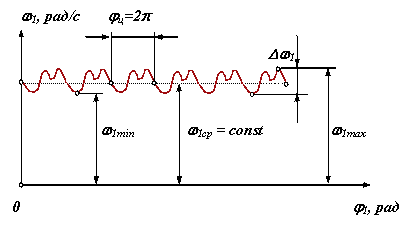постоянна, где- частота вращения начального звена агрегата.



В машинах, приведенный момент инерции которых зависит от обобщенной координаты, на неравномерность движения оказывает влияние величина изменения приведенного момента инерции. Колебания скорости изменения обобщенной координаты машины не оказывают прямого влияния на фундамент машины. Поэтому эти колебания и вызывающие их причины определяют, так называемую, внутреннюю виброактивность машины.

11. построение кинематических диаграмм на примере кривошипно-ползунного механизма

Построение кинематических диаграмм

В качестве примера рассмотрим построения кинематических диаграмм S_C=S_C(t) для перманентного движения точки «С» кривошипно-ползунного механизма АВС, т. е. когда кривошип вращается с постоянной угловой скоростью .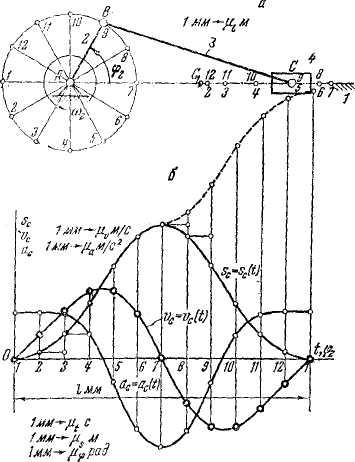



Рис.3.1 Кривошипно- ползунный механизм:

S_C=S_C(t); - диаграмма перемещения

V_c= V_c(t); - диаграмма скорости

а_с= а_с(t); - диаграмма ускорения

Для этого произведем разметку путей точек В и С. Отчет перемещений точки С удобно вести от крайнего левого положения ползуна. Проводим оси координат и на оси абсцисс откладываем отрезок l _MM, представляющей собой в масштабе время Т одного полного оборота кривошипа, т.е. Т=

где: n-частота вращения кривошипа в оборотах в минуту,

тогда 

Построение диаграммы перемещения

Отрезок l разбиваем на 12 равных частей и в соответствующих точках 1,2,3 и т. д. откладываем расстояние пройденные точкой «С» от крайнего левого положения С₁ ползуна. Так в точке 2 откладываем в направлении параллельном оси ординат, отрезок С₁С₂; точке 3-отрезок С₁С₃ , и т.д.

Если отрезки С₁,С₂, С₁С₃ откладывать прямо со схемы (Рис. а), то

масштаб диаграммы S_C=S_C(t)по оси ординат будет равен μ_i, т.е. масштабу

построения схемы. С положения С₇, когда точка С займет крайнее правое

положение, расстояния С7С8, С7С9 вычитаются из ординаты С1С7, отложенной в положении С7, и, таким образом, кривая S_C=S_C(t) в положении, когда кривошип 2 придет в начальное положение, будет иметь ординату, равную нулю.

Полученная кривая является кривой расстояний точки С от крайнего

левого положения ползуна. Если надо построить кривую путей, пройденных

точкой С, то от положения С_7, расстояния С₇С₈, С₇С₉ надо прибавлять к ранее отложенному отрезку С₁С₇, на рис. б) – часть кривой путей показана штрихами. Т.к. кривошип вращается с постоянной угловой скоростью ₂, то можно считать, что по оси абсцисс отложено не время t, а углы поворота φ₂ звена 2 , т.е. диаграммы S_C=S_C(t), будут одновременно и диаграммами S_C=S_C(φ₂). Масштаб μ_φ= 2π/l , где отрезок l должен быть взят с чертежа в мм.

Построение диаграмм скоростей и ускорений методом

графического дифференцирования

Имея кинематическую диаграмму перемещений звена, можно получить диаграмму скоростей путем графического дифференцирования. Рассмотрим последовательность построения диаграммы скоростей методом хорд.

1. 
   На диаграмме перемещений проводим хорды: оа, ав, и т.д.
   

2. Строим оси координат для диаграммы скоростей и на продолжении оси

абсцисс (ot) влево, откладываем полюсное расстояние (ОР_V) в пределах

= 30 – 60 мм.

3. Из полюса Р_V проводим лучи: 1, 2, 3, …, и т. д. параллельные хордам

оа, ав, и т.д. до пересечения с осью ординат в точках: 1^’, 2^’, 3^’, ….

4. Из точек 1^’, 2^’, 3^’, проводим горизонтальные линии до середины

соответствующих отрезков времени (1^’’, 2 ^‘’, 3 ^‘’, …).

5. Полученные точки соединяем плавной кривой.

6. Вычисляем масштаб скоростей.



При дифференцировании диаграммы угловых перемещений получаем соответственно диаграмму угловых скоростей в масштабе:

 

Для получения графика ускорений производим графическое дифференцирование графика скоростей. При этом: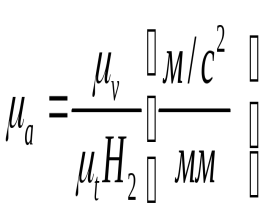

;

При дифференцировании графика скоростей необходимо обратить внимание на определение величины ускорения в нулевом (12) положении.

Для этого надо воспользоваться хордой (12 - 1), продолжив график скоростей в следующий цикл.

Масштаб времени можно вычислить по формуле

,

где Т – период одного оборота кривошипа, с; L_X – длина отрезка между точками 1 и 1 на графике (диаграмме) перемещений, мм.

Так как период Т можно вычислить по формулам

, или , с,

где ω₁ – угловая скорость кривошипа, 1/с; n₁ – частота вращения кривошипа, об/мин, то масштаб времени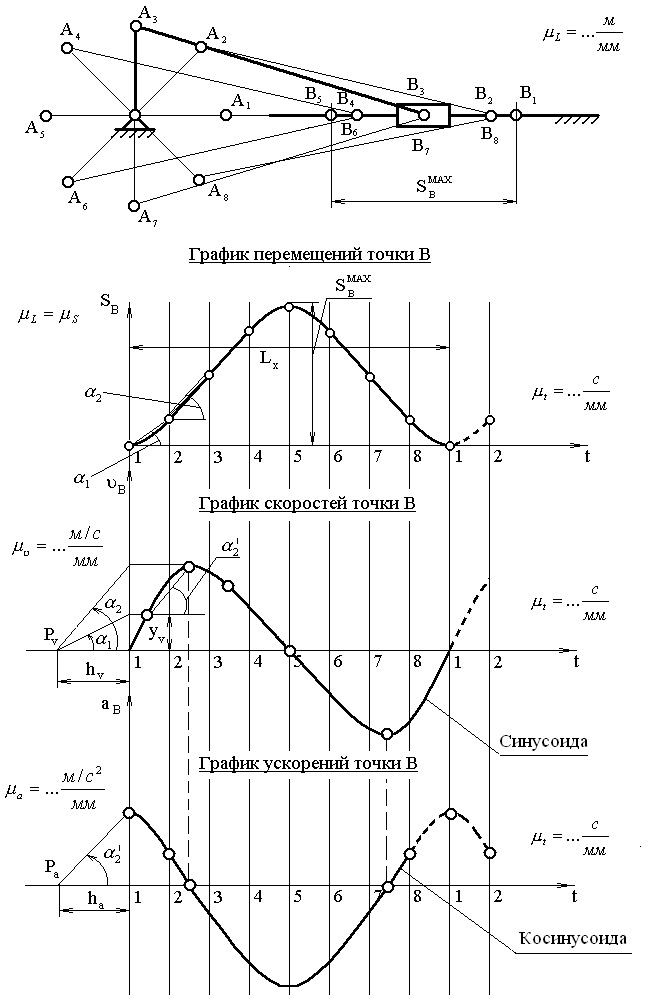

, с/мм.



Рис. 3.2

12. кинетическая энергия механизма. Приведенная масса. Приведенный момент инерции

Кинетическая энергия механизма

Для i-го звена, совершающего сложное движение (например, для шатуна кривошипно-ползунного механизма), кинетическую энергию можно выразить формулой

,

где первое слагаемое правой части – это кинетическая энергия поступательного движения центра масс звена; второе слагаемое – кинетическая энергия вращательного движения; mi – масса звена; Vsi – скорость центра масс; Jsi – момент инерции звена относительно центра масс;  – угловая скорость звена.

Для всего механизма кинетическая энергия равна сумме кинетических энергий всех звеньев механизма:

                               (1)

где n – количество подвижных звеньев.

 

Приведенная масса механизма

Условно заменим механизм его динамической моделью. Например, кривошипно-ползунный механизм заменим динамической моделью, состоящей из стойки и кривошипа.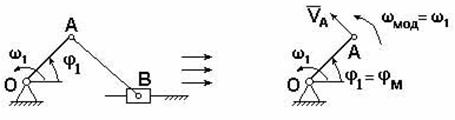



            Рис. 5.2. Замена кривошипно-ползунного механизма динамической моделью

 

Здесь ОА – звено приведения механизма, в котором как бы сосредоточена инертность всех звеньев механизма, А – точка приведения.

Уравнение (1) умножим и разделим на квадрат скорости точки приведения VA: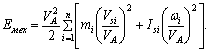



Выражение в квадратных скобках имеет размерность массы (кг) и называется приведенной массой mпр механизма в точке А.

Тогда



где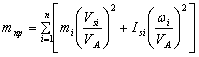

.                                   (2)

Приведенной массой механизма называется такая условная масса, которая как бы сосредоточена в точке приведения механизма, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма.

 

Приведенный момент инерции

Так как , где  – длина звена приведения,  – его угловая скорость, то кинетическую энергию механизма можно выразить уравнением



где приведенный момент инерции механизма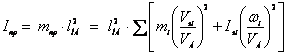

.                     (3)

Приведенным моментом инерции механизма называется такой условный момент инерции, которым как бы обладает звено приведения относительно оси вращения, кинетическая энергия которого (при таком моменте инерции) равна сумме кинетических энергий всех звеньев механизма.

Величины mпр и Jпр не являются постоянными для данного механизма, а меняют свое численное значение в зависимости от положений звеньев, так как звенья меняют свои скорости.

 

Пример 1.

Определить приведенную массу и приведенный момент инерции

линейные и угловые скорости звеньев и центров масс звеньев: 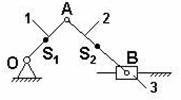,  и  – скорости центров масс кривошипа, шатуна и ползуна,  и  – угловые скорости кривошипа и шатуна.

       

Рис. 5.3. Кривошипно-ползунный механизм

 

Пусть кривошип 1 – звено приведения, А – точка приведения.

Приведенная масса механизма вычисляется по формуле

,

а приведенный момент инерции согласно (3) – по формуле

.