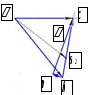
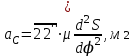Примеры. Исследование рычажного механизма Исходные данные Дана схема (рис. 2), частота вращения ведущего звена n
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
1 2 Примеры выполнения курсовой работы.Тема 1. Кинематическое исследование рычажного механизма 1.1. Исходные данные Дана схема (рис. 2), частота вращения ведущего звена nAB = 950 об/мин и длины звеньев rAB = 110 мм, lBC = 460 мм, lBD = 290 мм. Исследование механизма производится в 11-ом положении (заданный угол поворота кривошипа ).  Рис. 2. Схема механизма 1.2. Описание построения плана механизма Принимаем длину кривошипа 1 на чертеже равной 40 мм. Расчет масштабного коэффициента производим по формуле
где 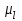 – масштабный коэффициент, м/мм; – масштабный коэффициент, м/мм;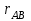 – длина кривошипа по заданию, м; – длина кривошипа по заданию, м;AB – длина кривошипа на чертеже, мм. 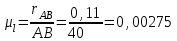 . .Расчет длин звеньев механизма на чертеже ведем, используя следующую формулу
Где  – длина звена на чертеже, мм; – длина звена на чертеже, мм;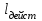 – действительная длина звена, м; – действительная длина звена, м;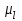 – масштабный коэффициент, м/мм. – масштабный коэффициент, м/мм. ; ; . .1.3. Структурный анализ механизма Составим описание звеньев и кинематических пар механизма и занесём их соответственно в таблицу 1.1 и таблицу 1.2. Таблица 1.1 Характеристика звеньев механизма
Таблица 1.2 Характеристика кинематических пар механизма
Степень свободы плоского механизма находится по формуле Чебышева
где 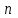 – число подвижных звеньев, в данном механизме их 5 (табл. 1.1); – число подвижных звеньев, в данном механизме их 5 (табл. 1.1); – число одноподвижных кинематических пар 5 класса, в данном механизме их 7 (табл. 1.2); – число одноподвижных кинематических пар 5 класса, в данном механизме их 7 (табл. 1.2); – количество двухподвижных пар 4 класса, в данном механизме их нет (табл. 1.2). – количество двухподвижных пар 4 класса, в данном механизме их нет (табл. 1.2). . .1.4. Построение кинематических диаграмм По найденным на планах механизма положениям ведомого звена 5 вычерчиваем график перемещения ползуна B, начиная от крайнего нижнего положения. Время оборота ведущего звена (кривошипа AВ) найдем по формуле
где  – время оборота кривошипа АВ, с; – время оборота кривошипа АВ, с;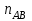 – частота вращения кривошипа АВ, об/мин. – частота вращения кривошипа АВ, об/мин.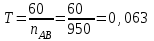 . .Изобразим это время на оси абсцисс отрезком x = 159 мм. Масштабный коэффициент времени на диаграмме рассчитывается по формуле
где  – масштабный коэффициент времени на диаграмме, с/мм; – масштабный коэффициент времени на диаграмме, с/мм; – время оборота кривошипа АВ, с; – время оборота кривошипа АВ, с; – принятая длина отрезка по оси абсцисс, мм. – принятая длина отрезка по оси абсцисс, мм.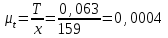 . .Масштаб перемещений на диаграмме, откладываемых по оси ординат, принимаем равным величине удвоенного масштаба длины на схеме механизма. 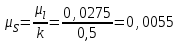 где 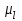 =0,00275 – масштабный коэффициент плана положений механизма, м/мм; =0,00275 – масштабный коэффициент плана положений механизма, м/мм;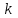 – коэффициент уменьшения (увеличения) диаграммы перемещений по сравнению с планом положений; – коэффициент уменьшения (увеличения) диаграммы перемещений по сравнению с планом положений;Масштабный коэффициент угла поворота кривошипа найдем по формуле
где 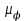 – масштабный коэффициент угла поворота кривошипа, рад/мм; – масштабный коэффициент угла поворота кривошипа, рад/мм; – масштабный коэффициент времени на диаграмме, м/мм; – масштабный коэффициент времени на диаграмме, м/мм; – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;Угловую скорость звена 1 можно найти по следующей формуле
где  – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;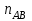 – частота вращения кривошипа АВ, об/мин. – частота вращения кривошипа АВ, об/мин. . .Тогда 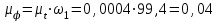 . .Дифференцируя график перемещений, получим график изменения скорости ведомого звена. Дифференцирование проводим графически методом хорд. Вычисляем масштабный коэффициент скорости на диаграмме
где 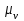 – масштабный коэффициент скорости на диаграмме, м·с-1/мм; – масштабный коэффициент скорости на диаграмме, м·с-1/мм;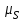 – масштабный коэффициент перемещений на диаграмме, м/мм; – масштабный коэффициент перемещений на диаграмме, м/мм; – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;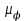 – масштабный коэффициент угла поворота кривошипа, рад/мм; – масштабный коэффициент угла поворота кривошипа, рад/мм; – полюсное расстояние, мм. – полюсное расстояние, мм.Полюсное расстояние Hv принимаю равным 40 мм. Тогда  . .Аналогичным способом получим кривую ускорения, дифференцируя график скорости. Вычисляем масштабный коэффициент ускорения на диаграмме
где 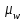 – масштабный коэффициент ускорения на диаграмме, м·с-2/мм; – масштабный коэффициент ускорения на диаграмме, м·с-2/мм;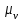 – масштабный коэффициент скорости на диаграмме, м·с-1/мм; – масштабный коэффициент скорости на диаграмме, м·с-1/мм; – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;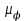 – масштабный коэффициент угла поворота кривошипа, рад/мм; – масштабный коэффициент угла поворота кривошипа, рад/мм; – полюсное расстояние, мм. – полюсное расстояние, мм. . .1.5. Описание построения плана скоростей От произвольно взятой точки Р отложим вектор скорости  , который направлен перпендикулярно кривошипу в направлении , который направлен перпендикулярно кривошипу в направлении  . Принимаем длину вектора . Принимаем длину вектора  на плане скоростей равной 40 мм. на плане скоростей равной 40 мм.Вращение кривошипа задано схемой механизма и направлено против часовой стрелки. Скорость точки B кривошипа можно найти, предварительно рассчитав угловую скорость вращения кривошипа
где  – скорость точки В кривошипа, м/с; – скорость точки В кривошипа, м/с; – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;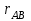 – длина кривошипа по заданию, м. – длина кривошипа по заданию, м. Расчет масштабного коэффициента скорости
где  – масштабный коэффициент скорости, м·с-1/мм; – масштабный коэффициент скорости, м·с-1/мм; – скорость точки В кривошипа, м/с; – скорость точки В кривошипа, м/с;Pb – длина вектора Pb на плане скоростей, мм.  . .Для каждого из 12-и положений: Скорость точки C ползуна найдем, решив совместно два векторных уравнения
Первое уравнение описывает движение т. С относительно т. В, а второе описывает движение т. С, принадлежащей ползуну. Скорость точки D ползуна найдем, решив совместно два векторных уравнения
Первое уравнение описывает движение т. D относительно т. В, а второе описывает движение т. D, принадлежащей ползуну. Векторы скоростей 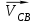 и и  строим из т. B перпендикулярно шатунам 2 и 4 до их пересечения с осью xx. строим из т. B перпендикулярно шатунам 2 и 4 до их пересечения с осью xx.1.6. Описание построения плана ускорений От полюса Π отложим вектор нормального ускорения в направлении от В к А в виде вектора  . .Нормальное (центростремительное) ускорение т. В кривошипа найдем по формуле
где 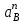 – нормальное ускорение т. В, м/с2; – нормальное ускорение т. В, м/с2; – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;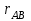 – длина кривошипа по заданию, м – длина кривошипа по заданию, м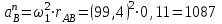 . .Принимаем длину вектора 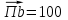 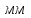 . .Расчет масштабного коэффициента ускорения проведем по формуле
где  – масштабный коэффициент ускорения, м·с-2/мм; – масштабный коэффициент ускорения, м·с-2/мм;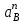 – нормальное ускорение т. В, м/с2; – нормальное ускорение т. В, м/с2;Πb – длина вектора Πb на плане скоростей, мм.  . .Для каждого из 2-ух положений: Ускорение точки C найдем, решив совместно два векторных уравнения
Ускорение точки D найдем, решив совместно два векторных уравнения
Нормальные ускорения  и и  строим параллельно шатунам 2 и 4 соответственно, причем они направлены от т. С и D к т. В. строим параллельно шатунам 2 и 4 соответственно, причем они направлены от т. С и D к т. В.Тангенциальные ускорения  и и  строим перпендикулярно нормальным ускорениям строим перпендикулярно нормальным ускорениям 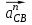 и и  из конца векторов до пересечения с осью xx. из конца векторов до пересечения с осью xx.Для «0-го» положения: Нормальное ускорение  определим по формуле определим по формуле
где  – нормальное ускорение звена CB, м/с2; – нормальное ускорение звена CB, м/с2;cb – длина вектора cb скорости шатуна СВ на чертеже, мм; 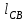 – действительная длина шатуна CB, м. – действительная длина шатуна CB, м. ; ;На плане ускорений длина вектора ncb будет равна
где  – длина вектора нормального ускорения точки B кривошипа, мм; – длина вектора нормального ускорения точки B кривошипа, мм; – нормальное ускорение звена CB, м/с2; – нормальное ускорение звена CB, м/с2; – масштабный коэффициент ускорения, м·с-2/мм. – масштабный коэффициент ускорения, м·с-2/мм. . .Нормальное ускорение  найдем по формуле (1.18) найдем по формуле (1.18) . .А длину вектора  по формуле (1.19) по формуле (1.19) . .Для «11-го» положения: Нормальное ускорение  определим по формуле (1.18) определим по формуле (1.18) ; ;На плане ускорений длина вектора 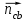 будет равна (1.19) будет равна (1.19) . .Нормальное ускорение  найдем по формуле (1.18) найдем по формуле (1.18) . .А длину вектора 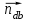 по формуле (1.19) по формуле (1.19) . .Тангенциальное ускорение звена СВ находим из плана ускорений по формуле
где 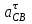 – тангенциальное ускорение звена CB, м/с2; – тангенциальное ускорение звена CB, м/с2;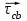 – величина вектора τСВ на плане ускорений; – величина вектора τСВ на плане ускорений; – масштабный коэффициент ускорения, м·с-2/мм. – масштабный коэффициент ускорения, м·с-2/мм.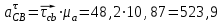 ; ;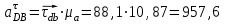 . .Сравнительный анализ Рассчитаем скорость и ускорение выходного звена, полученные построением планов скоростей. Для этого умножаем длину вектора абсолютной скорости ползуна С на масштабный коэффициент плана скоростей и длину вектора абсолютного ускорения на масштабный коэффициент плана ускорений:
Рассчитаем скорость и ускорение выходного звена, полученные построением диаграммы скоростей. Для этого умножаем ординату диаграммы скорости ползуна С на масштабный коэффициент диаграммы скоростей и ординату диаграммы ускорения на масштабный коэффициент диаграммы ускорений (например, для второго положения механизма):
Сравним полученные значения Таблица 1.3 Сравнительный анализ скоростей и ускорений
 1 2 |

 ,
, ,
,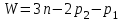 ,
,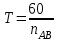 ,
,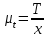 ,
, ,
,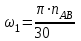 ,
, ,
, ,
, ,
, ,
,

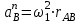
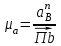


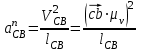 ,
, ,
, ,
,