курсовая по ТММ. Ненахов Илья КР ТММ. Структурное, кинематическое и кинетостатическое исследование плоского рычажного механизма
 Скачать 288.48 Kb. Скачать 288.48 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН АКАДЕМИЯ ЛОГИСТИКИ И ТРАНСПОРТА Кафедра: Магистральная инженерия КУРСОВАЯ РАБОТА Тема: Структурное, кинематическое и кинетостатическое исследование плоского рычажного механизма Дисциплина: _Теория машин и механизмов_ Выполнил:__ Ненахов И.С.____ Группа:____УСД-Л-20-1____ Проверил:___Жадраев Р. Ж._____ Алматы 2021 Академия логистики и транспорта Кафедра «Магистральная инженерия» Утверждаю: Зав. кафедрой «МИ»  Аширбаев Г.К. Аширбаев Г.К.«16»_09_ 2021_ г., Протокол № 1 ЗАДАНИЕ на выполнение курсовой работы по дисциплине «Теория механизмов и машин» на тему: «Структурное, кинематическое и кинетостатическое исследование плоского рычажного механизма» Задание выдано студенту __ Ненахов И.С._группы _____УСД-Л-20-1___ ВАРИАНТ № _4 - 2__ Схема механизма 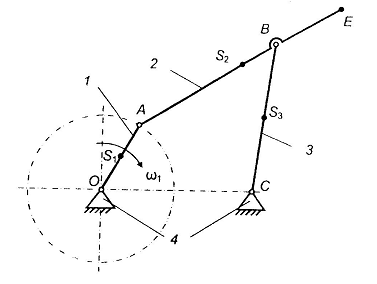 Исходные данные:
Задание выдал (а)________ Дата выдачи «____25____» ______09____________ 202 1____ г. Срок сдачи «___10_____» ________12__________ 202 1____ Провести кинематический и кинетостатический анализ для механизма шарнирного четырехзвенника . Угловая скорость кривошипа (звено 1) постоянна. 
1.КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА. Структурный анализ механизма k = 4 – количество звеньев n = 3 – количество подвижных звеньев p5 = 4 – количество кинематических пар 5-го класса О(0,1) кинематическая пара 5-го класса; А(1,2) кинематическая пара 5-го класса; В (2,3) кинематическая пара 5-го класса; С(3,0) кинематическая пара 5-го класса. Степень подвижности механизма:w = 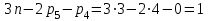 . .Механизм образован присоединением к ведущему звену ОА (звено 1) и стойке (звено 0) группы, состоящей из звеньев 2 и 3. Построение 12 планов положения механизма. Для подсчёта масштабного коэффициента μl длиной звена ОА на чертеже задаёмся произвольно. Из таблицы исходных данных все длины переводим в миллиметры. lOA = 0,08м; lOC = 0.16 м; lBC = 0,2 м; lAB = 0,2 м; lBE = 0,18 м. Длину отрезка ОА, изображающего на чертеже размер ведущего звена, принимаем равной 50 мм т.е. ОА = 50 мм. Тогда масштаб схемы механизма будет 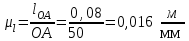 , ,и по нему из таблицы исходных данных длины звеньев ОС, АВ, ВС, ВЕ переводим в мм: 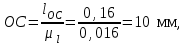 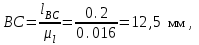 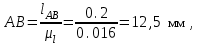 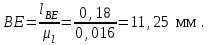 При построении плана положения механизма пользуемся методом засечек. Вначале отмечаем на чертеже положение неподвижных элементов кинематических пар. Строим 12 равностоящих положений ведущего звена. На этом чертеже изображаем планы положений остальных звеньев механизма и положение т. Е. Затем соединяем плавной линией положения этой точки и получаем траекторию этой точки (шатунную кривую) рис . 1.3. Построение плана скоростей Для каждого положения механизма определяются скорости точек графическим методом. Вначале определяем скорость точки A, принадлежащей ведущему звену, вращающегося равномерно с угловой скоростью 1. Скорость этой точки по  модулю равна: модулю равна: 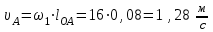  и направлена перпендикулярно ОА в соответствии с направлением угловой скорости 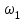 . Выбираем в качестве полюса плана скоростей точку р. скорость точки A ( . Выбираем в качестве полюса плана скоростей точку р. скорость точки A (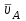 ) на плане скоростей строим в виде вектора pa, от полюса р, длиной которого задаёмся. ) на плане скоростей строим в виде вектора pa, от полюса р, длиной которого задаёмся.Принимаем pa = 100 мм. Вычисляем масштаб плана скоростей: 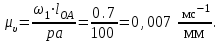 Строим план скоростей для группы звеньев 2, 3. Построение ведем по следующим двум векторным уравнениям: 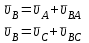 , ,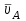 скорость точки А по модулю равная скорость точки А по модулю равная 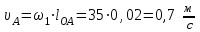 и направленная перпендикулярно линии АВ в сторону, соответствующую направлению угловой скорости звена ОА; 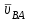 скорость точки B при вращении звена АВ вокруг оси шарнира А, по модулю неизвестная и направленная перпендикулярно линии АВ; скорость точки B при вращении звена АВ вокруг оси шарнира А, по модулю неизвестная и направленная перпендикулярно линии АВ;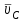 скорость точки С равная нулю; скорость точки С равная нулю;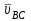 скорость точки В при вращении звена ВС вокруг оси шарнира С, по модулю неизвестная и направленная перпендикулярно линии ВС. скорость точки В при вращении звена ВС вокруг оси шарнира С, по модулю неизвестная и направленная перпендикулярно линии ВС.Построение плана скоростей ведем в следующей последовательности (рис. ). Строим решение первого векторного уравнения, указанного выше. От полюса р плана откладываем отрезок (ра), изображающий скорость т. A ( 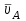 ), перпендикулярно линии ОА в соответствии с направлением вращения звена ОА. Длину этого отрезка принимаем равной (ра) = (ОА) = 50 мм. Через точку а проводим направление скорости ), перпендикулярно линии ОА в соответствии с направлением вращения звена ОА. Длину этого отрезка принимаем равной (ра) = (ОА) = 50 мм. Через точку а проводим направление скорости 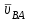 линию, перпендикулярную АВ. Переходим к построению решения второго векторного уравнения, указанного выше. Скорость точки С равна нулю ( линию, перпендикулярную АВ. Переходим к построению решения второго векторного уравнения, указанного выше. Скорость точки С равна нулю (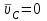 ), поэтому точку с совмещаем с полюсом р. Через точку p проводим направление скорости ), поэтому точку с совмещаем с полюсом р. Через точку p проводим направление скорости 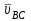 линию, перпендикулярную ВС, до пересечения с линией, проведенной перпендикулярно АВ, и получаем точку в конец вектора скорости точки В линию, перпендикулярную ВС, до пересечения с линией, проведенной перпендикулярно АВ, и получаем точку в конец вектора скорости точки В 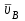 . Скорость точки Е ( . Скорость точки Е (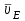 ) находим по правилу подобия: конец вектора этой скорости (точка е) должен лежать на линии ав в том же отношении в каком точка Е лежит на АВ. ) находим по правилу подобия: конец вектора этой скорости (точка е) должен лежать на линии ав в том же отношении в каком точка Е лежит на АВ.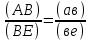 . .Отсюда 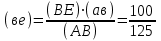 Искомая скорости точки В (В) и точки Е (Е) равна: 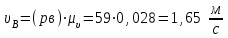 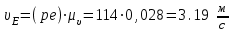 . .1.4. Построение плана ускорений. Ускорения находятся методом плана ускорений. Строим план ускорений для группы звеньев 2, 3. Этот план строится по таким двум векторным уравнениям: 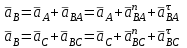 , ,где 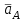 нормальное ускорение (оно же и полное) точки А, по модулю равное нормальное ускорение (оно же и полное) точки А, по модулю равное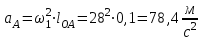 и направленное параллельно линии ОА от точки А к точке О; 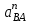 нормальное ускорение точки В во вращательном движении звена АВ относительно точки А, по модулю равное нормальное ускорение точки В во вращательном движении звена АВ относительно точки А, по модулю равное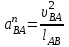 , ,и направленное параллельно линии АВ от точки В к точке А; 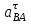 касательное ускорение точки В в том же движении звена АВ, по модулю равное касательное ускорение точки В в том же движении звена АВ, по модулю равное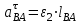 (2 угловое ускорение звена АВ, пока нам неизвестное) и направленное перпендикулярно линии АВ; 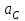 ускорение точки С, равное нулю ( ускорение точки С, равное нулю (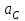 = 0); = 0); 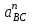 нормальное ускорение точки В во вращательном движении звена ВС относительно точки С, по модулю равное нормальное ускорение точки В во вращательном движении звена ВС относительно точки С, по модулю равное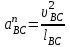 , ,и направленное параллельно линии ВС от точки В к точке С; 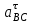 - касательное ускорение той же точки в том же движении звена ВС равное - касательное ускорение той же точки в том же движении звена ВС равное 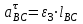 (3 угловое ускорение звена ВС, пока нам неизвестное) и направленное перпендикулярно линии ВС; Построение плана ускорений ведём в следующей последовательности (рис. -----). Строим решение первого векторного уравнения указанного выше, для чего от полюса плана откладываем отрезок (а) изображающий ускорение 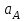 , параллельно линии ОА. Длину (а) принимаем равной (а) = 100 мм, от чего масштаб плана ускорения будет , параллельно линии ОА. Длину (а) принимаем равной (а) = 100 мм, от чего масштаб плана ускорения будет 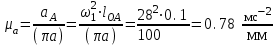 от точки а откладываем отрезок ( 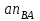 ), изображающий ускорение ), изображающий ускорение 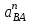 ; ; Длина отрезка ( |

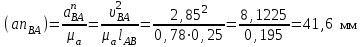
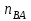 проводим направление касательного ускорения
проводим направление касательного ускорения 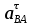 линию перпендикулярную линии AB. Затем переходим к решению второго векторного уравнения, указанного выше. Точку с совмещаем с точкой , так как (аС = 0), от точки откладываем отрезок (
линию перпендикулярную линии AB. Затем переходим к решению второго векторного уравнения, указанного выше. Точку с совмещаем с точкой , так как (аС = 0), от точки откладываем отрезок (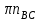 ), изображающий нормальное ускорение
), изображающий нормальное ускорение 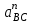 , его длина равна
, его длина равна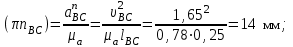
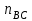 проводим направление ускорения
проводим направление ускорения 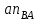 линией, перпендикулярной АВ. Точка пересечения в представляет собой конец вектора ускорения аВ.
линией, перпендикулярной АВ. Точка пересечения в представляет собой конец вектора ускорения аВ.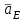 ) точку е находим по правилу подобия из соотношения:
) точку е находим по правилу подобия из соотношения: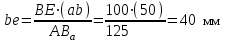
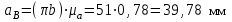
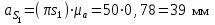
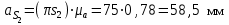
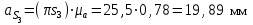
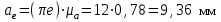
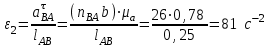
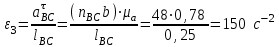 .
.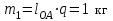
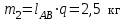
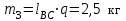
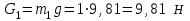
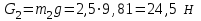
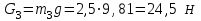
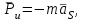
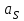 – ускорение центра масс
– ускорение центра масс 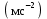
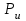 противоположно направлению вектора
противоположно направлению вектора 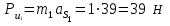
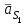
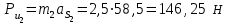
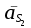 этого звена.
этого звена.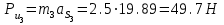
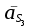 этого звена.
этого звена.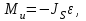
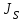 момент инерции масс звена относительно оси проходящей через его
момент инерции масс звена относительно оси проходящей через его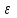 угловое ускорение звена (сек‾²)
угловое ускорение звена (сек‾²)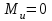 , так как звено вращается равномерно.
, так как звено вращается равномерно.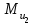 найдем по формуле
найдем по формуле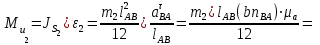
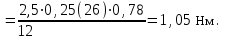
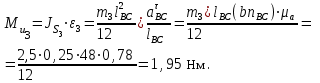
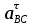 тангенциального ускорения точки В во вращении звена ВС относительно точки С.
тангенциального ускорения точки В во вращении звена ВС относительно точки С. 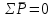
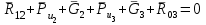 (1)
(1)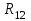 , величина и направление реакции
, величина и направление реакции 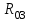 .
.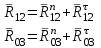
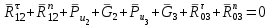 (2)
(2)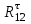 найдем, рассматривая равновесие звена 2. Звено 2 находится под действием следующих сил: силы инерции
найдем, рассматривая равновесие звена 2. Звено 2 находится под действием следующих сил: силы инерции 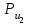 , составляющих
, составляющих 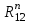 и
и 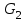 и момента инерции
и момента инерции 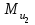 . Напишем равенство нулю суммы моментов всех сил относительно точки В, приложенных к звену 2 (тем самым исключим из него момент неизвестной реакции
. Напишем равенство нулю суммы моментов всех сил относительно точки В, приложенных к звену 2 (тем самым исключим из него момент неизвестной реакции 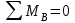 ,
,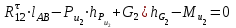 .
.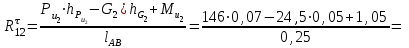
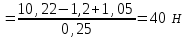
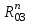 ).
).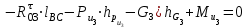
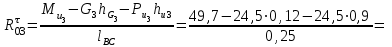
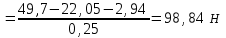
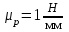
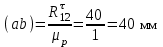
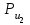 в виде отрезка (bc)
в виде отрезка (bc)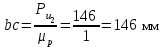
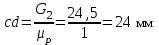
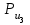 в виде отрезка (de)
в виде отрезка (de)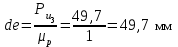
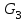 в виде отрезка (ef)
в виде отрезка (ef)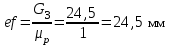
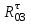 в виде отрезка
в виде отрезка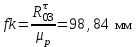
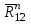 , а через точку k – прямую параллельную ВС, она будет линией действия
, а через точку k – прямую параллельную ВС, она будет линией действия 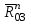 . Находим точку пересечения l этих двух прямых. Отрезок (al) в масштабе
. Находим точку пересечения l этих двух прямых. Отрезок (al) в масштабе 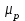 дает искомую величину
дает искомую величину 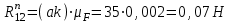
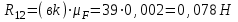
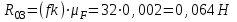
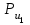 , сила
, сила 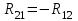 , сила (реакция)
, сила (реакция) 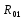 и уравновешивающая сила
и уравновешивающая сила 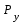 .
.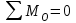
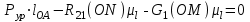
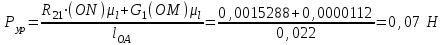
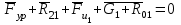 (3)
(3)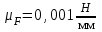
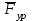 отложим от точки а в виде отрезка (ав)
отложим от точки а в виде отрезка (ав)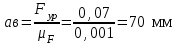
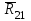 в виде отрезка (вc)
в виде отрезка (вc)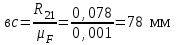
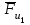 в виде отрезка (cd)
в виде отрезка (cd)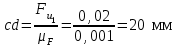
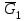 в виде отрезка (de)
в виде отрезка (de)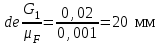
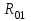 равна:
равна: