1. Частотные и переходные характеристики систем авторегулирования
 Скачать 222.73 Kb. Скачать 222.73 Kb.
|
|
Введение Радиопередающие устройства (РПдУ) применяются в сферах телекоммуникации, телевизионного и радиовещания, радиолокации, радионавигации. Стремительное развитие микроэлектроники, аналоговой и цифровой микросхемотехники, микропроцессорной и компьютерной техники оказывает существенное влияние на развитие радиопередающей техники как с точки зрения резкого увеличения функциональных возможностей, так и с точки зрения улучшения ее эксплуатационных показателей. Это достигается за счет использования новых принципов построения структурных схем передатчиков и схемотехнической реализации отдельных их узлов, реализующих цифровые способы формирования, обработки и преобразования колебаний и сигналов, имеющих различные частоты и уровни мощности. 1. Частотные и переходные характеристики систем авторегулирования Частотная и переходная характеристики замкнутой системы являются показателями качества при гармоническом и скачкообразном воздействиях. Если задающее воздействие гармоническое: xз(t) = Acost, то выходной процесс линейной системы тоже гармонический: y(t) = AKз()cos(t + з()), где Кз() и з(), соответственно, - АЧХ и ФЧХ замкнутой системы. (t) = xз(t) – y(t) = Acost – AKз()cos(t + з()) будет равна нулю только при Кз() = 1 и з() = 0. Это требование к идеальной частотной характеристике замкнутой системы. Если все составляющие спектра задающего воздействия попадают в область частот, где частотная характеристика идеальна, то воздействие отрабатывается без ошибки. В противном случае возникает динамическая ошибка.Для оценки качества регулирования по АЧХ замкнутой системы используется показатель колебательности М = Кмакс/Кз(0) (см. рис. 1). Обычно величина показателя колебательности меньше 2.  Рис.1 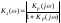 Так как АЧХ будет близка к 1, если Кр()>>1, независимо от вида частотной характеристики разомкнутой системы в этой области частот. Для примера рассмотрим системы авторегулирования разного типа: статическую и астатические первого и второго порядка, передаточные функции которых описываются выражениями: 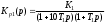 , ,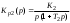 , , 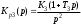 .(1) .(1)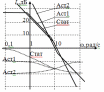 Рис. Их логарифмические амплитудные характеристики, как видно из рис. 2, значительно отличаются в области нижних и верхних частот. Однако если запасы устойчивости в этих системах одинаковы, то различие в амплитудно-частотных характеристиках замкнутых систем невелико (см. рис. 3). Запас устойчивости по фазе для каждой из этих систем определяется выражениями: Δφ1 = 180 – arctg10ωсрT1 – arctgωсрТ1, Δφ2 = 90 – arctgωсрT2, (2) Δφ3 = arctgωсрТ3. По форме АЧХ можно судить о переходной характеристике системы. Так, если АЧХ будет монотонной, то и переходная характеристика монотонна, если в АЧХ будет подъем в области верхних частот, то переходная характеристика будет колебательной. Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4). 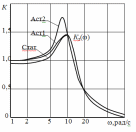 Рис. Обычно используются следующие числовые параметры переходной характеристики: время достижения первого максимума tm, время регулирования tрег, период колебаний на вершине Тв, перерегулирование Δhm/hуст. 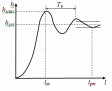 Рис. Так как частотная характеристика замкнутой системы однозначно связана с ЛАХ и ЛФХ разомкнутой системы, то можно установить связь, по крайней мере, качественную, между логарифмическими частотными характеристиками разомкнутой системы и параметрами переходной характеристики замкнутой системы. Так, чем меньше запас устойчивости по фазе, тем больше перерегулирование и медленнее затухание колебаний на вершине. Существует следующая приближенная связь между запасом устойчивости по фазе и перерегулированием: Δhm(в %) = 70 – Δφ(в град) при условии, что запас устойчивости по фазе 300 < < 700. Временные параметры переходной характеристики связаны с частотой среза ср.. Чем больше частота среза, тем шире полоса пропускания замкнутой системы и меньше все временные параметры. Как правило, системы, обладающие удовлетворительным качеством регулирования, имеют запас устойчивости по фазе от 30 до 700. Как можно обеспечить такой запас устойчивости по фазе? Если ЛАХ пересекает ось частот под наклоном -20 дБ/дек. и длина участка с таким наклоном достаточно велика, то запас устойчивости по фазе близок к 900. Такую связь можно установить, например, по логарифмическим частотным характеристикам интегрирующего звена. Во всем диапазоне частот его ЛАХ идет под наклоном –20 дБ/дек., а фазовый сдвиг равен –900. Если же ЛАХ пересекает ось частот под наклоном –40 дБ/дек. и длина участка с таким наклоном достаточно велика, то запас устойчивости по фазе близок к нулю. Поэтому такой наклон ЛАХ при пересечении оси частот нежелателен. Наиболее легко обеспечиваются приемлемые запасы устойчивости по фазе, если ЛАХ разомкнутой системы пересекает ось частот под наклоном –20 дБ/дек. и длина участка с таким наклоном составляет около 1,5 декады. С этим участком сопрягаются участки ЛАХ с наклонами –40 или –60 дБ/дек. Можно выделить 4 типа ЛАХ в окрестности частоты среза, отличающиеся наклонами: 1) -40, -20, -40; 2) -40, -20, -60; 3) -60, -20, -40; 4) -60, -20, -60. Если ЛАХ продлить в области нижних и верхних частот без изменения наклона, то передаточная функция разомкнутой системы для каждого из этих типов ЛАХ запишется, соответственно:
где Т1 = 1/ω1, Т2 = 1/ω2, К = 10L/20, L – значение ЛАХ на частоте ω1. Запас устойчивости по фазе зависит как от длины участка с наклоном –20 дБ/дек., так и от соотношения сопрягающих частот ω1 и ω2 и частоты среза ωср, а также от типа ЛАХ. Для соответствующего типа ЛАХ он определяется выражениями: Δφ1 = arctgωсрT1 – arctgωсрТ2, Δφ2 = arctgωсрТ1 – 2arctgωсрТ2, (4) Δφ3 = -900 + 2arctgωсрТ1 – arctgωсрТ2, Δφ4 = -900 + 2arctgωсрТ1 – 2arctgωсрТ2. Сравним запасы устойчивости по фазе для первого и четвертого типов ЛАХ при одинаковой длительности участка с наклоном –20 дБ/дек., равном 1,5 декады (см. рис. 5). ЛФХ, соответствующая ЛАХ первого типа, получается сложением ЛФХ двух интегрирующих звеньев, форсирующего звена с постоянной времени Т1 и инерционного звена с постоянной времени Т2. ЛФХ, соответствующая ЛАХ четвертого типа, получается сложением ЛФХ трех интегрирующих звеньев, двух форсирующих и двух инерционных звеньев. 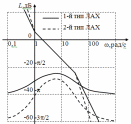 Рис. Видим, что с увеличением наклонов участков ЛАХ, сопрягаемых с участком с наклоном –20 дБдек., запас устойчивости по фазе становится меньше. Заметим также, что запас устойчивости по фазе уменьшается с приближением ср к 1 или 2. Для удобства сравнения процессов в системах, отличающихся друг от друга или передаточными функциями, или параметрами исследование проводится одновременно на трех моделях. Эти модели в изображении VisSim приведены на рис. 6.  Рис. Каждая содержит три линейных звена, задаваемых передаточными функциями. При моделировании статической и астатических систем первого и второго порядка используются только два звена. При этом передаточные функции (6) целесообразно представить в виде произведения передаточных функций отдельных звеньев: 2. Построение логарифмических частотных характеристик Логарифмические частотные характеристики можно определить, прологарифмировав комплексную частотную характеристику: lnK(j) = ln{K()Exp(j())} = lnK() + j(). Действительная часть полученного выражения является логарифмической АЧХ, а мнимая – логарифмической ФЧХ. Определенная таким образом логарифмическая АЧХ измеряется в неперах. Обычно используется другая единица измерения – децибел, и ЛАХ определяется как L() = 20lgK(). Главное достоинство логарифмических частотных характеристик проявляется при построении частотных характеристик последовательного соединения звеньев, так как логарифмические частотные характеристики складываются. Если передаточная функция линейной системы записывается как отношение полиномов, то ее можно представить в виде произведения сомножителей не выше второго порядка. Таких разнотипных сомножителей семь. В соответствии с этим вводятся семь типовых линейных звеньев: 1) безынерционное с передаточной функцией К(р) = К; 2) интегрирующее (К(р) = 1/р); 3) инерционное (К(р) = 1/(1 + рТ)); 4) колебательное (К(р) = 1/(1 + 2dTp + p2T2)); 5) дифференцирующее (К(р) = р); форсирующее (К(р) = 1 + рТ); 7) форсирующее второго порядка (К(р) = = 1 + 2dTp + p2T2). В настоящем лабораторном практикуме используются передаточные функции, составленные из типовых звеньев не выше первого порядка. Поэтому рассмотрим частотные характеристики только звеньев первого порядка. Комплексная частотная характеристика интегрирующего звена К(j) = 1/j. Логарифмическая АЧХ (ЛАХ) L() = 20lg(1/) = -20lg. Логарифмическая ФЧХ () = Arg(1/j) = -/2. Эти характеристики изображены на рис. П1. ЛАХ представляет собой прямую линию с наклоном --20дБ/дек., пересекающую горизонтальную ось на частоте = 1 рад/с. 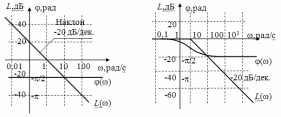 Рис. Комплексная частотная характеристика инерционного звена К(j) = =1/(1 + jT). ЛАХ: L() = 20lg(1/1 + 2T2) = -20lg1 + 2T2. ЛФХ: () = argK(j) = arctg(-T). Обе характеристики являются нелинейными функциями от lg. Построим сначала асимптотическую ЛАХ, составленную из низкочастотной и высокочастотной асимптот. Низкочастотная асимптота: L()0 = -20lg1 + 2T2 = 0. Высокочастотная асимптота: L() = = -20lg1 + 2T2 = -20lgT. Асимптоты пересекаются на частоте с= 1/Т, которую называют сопрягающей. Асимптотическая ЛАХ изображена на рис.8. Наибольшее отличие точной ЛАХ от асимптотической будет на сопрягающей частоте, и оно равно –20lg1 + с2Т2 = -20lg2 3 дБ. При отклонении частоты на октаву от сопрягающей отличие уменьшается до 1 дБ. При приближенном анализе таким отличием точной ЛАХ от асимптотической можно пренебречь и строить только асимптотические ЛАХ. Для построения ЛФХ можно воспользоваться таблицей Таблица.
ЛФХ инерционного звена приведена на рис. 8. Фазовый сдвиг на сопрягающей частоте равен -/4 и изменяется от 0 до -/2 практически за две декады: по одной в обе стороны от сопрягающей частоты. Логарифмические частотные характеристики дифференцирующего и форсирующего звеньев отличаются от характеристик интегрирующего и инерционного звеньев знаком. Они приведены на рис. 9 и рис. 10 соответственно. 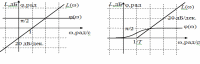 Рис. ЛАХ и ЛФХ последовательного соединения типовых линейных звеньев строятся сложением характеристик отдельных звеньев. Однако при построении ЛАХ удобнее складывать не их значения ,а наклоны. Можно пользоваться следующей методикой. 1. Определяются и наносятся на оси частот все сопрягающие частоты сi = 1/Ti. 2. На частоте = 1 наносится точка с координатой L1 = 20lgK, где К – коэффициент передачи разомкнутой системы. 3. Через эту точку проводится вспомогательная прямая с наклоном 20(l –k) дБ/дек., где l – количество дифференцирующих звеньев, k – количество интегрирующих звеньев. 4. По этой прямой проводится асимптотическая ЛАХ от нулевых частот до первой, самой низкой сопрягающей частоты. 5. Начиная с этой частоты наклон ЛАХ изменяется в соответствии с типом учитываемого звена: для инерционного на –20 дБ/дек., а для форсирующего на 20 дБ/дек. С таким наклоном ЛАХ проводится до следующей сопрягающей частоты и т.д. Пользуясь этой методикой, построим ЛАХ линейной системы с передаточной функцией К(р) = 100(1 + р)/р(1 + 10р)(1 + 0,01р)2. 1. Находим сопрягающие частоты: с1 = 1/10 = 0,1 рад/с, с2 = 1/1 = = 1 рад/с, с3 = 1/0,01 = 100 рад/с. 2. Находим L1 = 20lg100 = 40 дБ, так как К = 100. 3. Определяем наклон вспомогательной прямой. В передаточную функцию входит сомножитель 1/р, т.е. одно интегрирующее звено. Следовательно l = 0, k = 1 и наклон равен –20 дБ/дек. Строим эту прямую (см. рис.11). 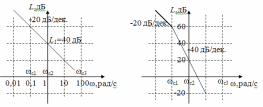 Рис. 4. По этой прямой проводится асимптотическая ЛАХ от нулевых частот до сопрягающей частоты с1 = 10 рад/с. Это сопрягающая частота инерционного звена с передаточной функцией 1/(1 + 10р), следовательно, наклон ЛАХ изменится на –20 дБ/дек и станет равным: –20 + + (-20) = -40 дБ/дек. (рис. 12). 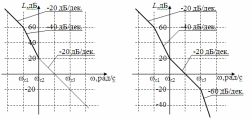 Рис. 5. ЛАХ с таким наклоном проводим до следующей сопрягающей частоты с2 = 1 рад/с. Так как это сопрягающая частота форсирующего звена, то наклон ЛАХ изменится на +20 дБ/дек и станет равным –40 + + 20 = -20 дБ/дек. (рис.13). 6. ЛАХ с наклоном –20 дБ/дек. проводится до следующей сопрягающей частоты с3 = 100 рад/с. Это сопрягающая частота инерционного звена. Таких звеньев два, и наклон становится равным: –20 + 2(-20) = = -60 дБ/дек. Далее сопрягающих частот нет, и ЛАХ с таким наклоном проводится до бесконечной частоты (рис. 14). ЛАХ построена. 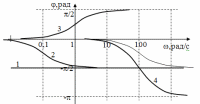 Рис. При построении ЛФХ линейной системы сначала строятся ЛФХ отдельных звеньев, как показано на рис. П9. Цифрами обозначены ЛФХ звеньев: 1 – интегрирующего, 2 – инерционного с Т1 = 10 с, 3 – форсирующего с Т2 = 1 с, 4 – двух инерционных с Т3 = 0,01 с. Сложив эти характеристики, получим ЛФХ системы (рис. 16). 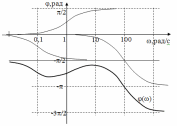 Рис. Заключение Основным направлением развития систем связи является обеспечение множественного доступа, при котором частотный ресурс совместно и одновременно используется несколькими абонентами. К технологиям множественного доступа относятся TDMA, FDMA, CDMA и их комбинации. При этом повышают требования и к качеству связи, т.е. помехоустойчивости, объему передаваемой информации, защищенности информации и идентификации пользователя и пр. Это приводит к необходимости использования сложных видов модуляции, кодирования информации, непрерывной и быстрой перестройки рабочей частоты, синхронизации циклов работы передатчика, приемника и базовой станции, а также обеспечению высокой стабильности частоты и высокой точности амплитудной и фазовой модуляции при рабочих частотах, измеряемых гигагерцами. Что касается систем вещания, здесь основным требованием является повышение качества сигнала на стороне абонента, что опять же приводит к повышению объема передаваемой информации в связи с переходом на цифровые стандарты вещания. Крайне важна также стабильность во времени параметров таких радиопередатчиков - частоты, модуляции. Очевидно, что аналоговая схемотехника с такими задачами справиться не в состоянии, и формирование сигналов передатчиков необходимо осуществлять цифровыми методами. Список литературы радиопередающий радиовещание замкнутый система Коновалов Г.Ф. Радиоавтоматика: Учебник для вузов. – М.: Радиотехника, 2003. Первачев С.В. Радиоавтоматика: Учебник для вузов. – М.: Радио и связь, 1982. Радиоавтоматика: Учебное пособие/ Под ред. В.А.Бесекерского. – М.: Высшая школа, 1985 Гришаев Ю.Н. Синтез частотных характеристик линейных систем автоматического регулирования: Метод. указания / РГРТА, 2000 Гришаев Ю.Н. Системы радиоавтоматики и их модели: учебное пособие.: Рязань,1977. Гришаев Ю.Н. Радиоавтоматика. компьютерный лабораторный практикум/ РГРТА.: Рязань, 2004 | |||||||||||||||||||||||||||||||||||

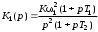 ,
,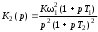 ,
,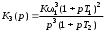 ,
,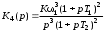 ,
,