Вопросы к экзамену по высшей математике 3 семестр. Матан_3семак. 1. Числовые ряды. Определение сходимости. Необходимое условие сходимости числового ряда
 Скачать 343 Kb.
|
 d=max – максимальный диаметр любой ячейкиСвойства:       7. (теорема о среднем) Если функция f(x,y) непрерывна на кривой L, то на ней найдётся такая точка  , что выполняется равенство  , где l-длина кривой L33. Вычисление криволинейных интегралов 1 рода 1) Явное задание   2) Параметрическое задание     3) Полярное задание   34. Криволинейные интегралы 2 рода. Свойства. Вычисление Опр. Если существует предел интегральной суммы  или  при  , то он называется криволинейным интегралом 2 рода   - общий криволинейный интеграл 2 родаСвойства:    Вычисление: 1) Явное задание  2) Параметрическое задание  35. Формула Грина Теорема: Если функции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными  в плоскости области D с границей L, то имеет место формула: (Движение по кривой такое, что D всегда слева)36. Условие независимости криволинейного интеграла 2 рода от пути интегрирования Теорема: Для того, чтобы криволинейный интеграл 2 рода не зависел от пути интегрирования в области D, необходимо и достаточно, чтобы в каждой точке выполнялось условие  Док-во:   37. Поверхностные интегралы 1 рода. Свойства. Вычисления. Опр. Поверхностный интеграл 1 рода от функции u=f(x,y,z) – предел интегральной суммы 1 рода при , если он не зависит ни от способа разбиения, ни от выбора точки Свойства.     Вычисление сводится к вычислению двойного интеграла по области - проекции S на плоскость хОу Явное задание:  38. Поверхностные интегралы 2 рода. Свойства. Вычисления. 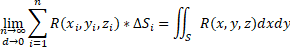  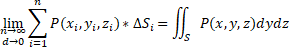 Свойства     5. Если - цилиндрические поверхности, то  Вычисление сводится к вычислению двойного интеграла  1. Метод проецирования на все координатные плоскости  2. Метод проецирования на одну координату  39. Формула Остроградского – Гаусса Пусть в пространстве Oxyz задана замкнутая поверхность S, которая является границей области V  40. Формула Стокса  41. Скалярное поле. Производная по направлению. Градиент Опр. Скалярное поле – числовая функция u, заданная в каждой точке M некоторой пространственной области Ω  – производная функции u по направлению lГрадиентом скалярного поля в точке M называют вектор  Между производной поля по направлению и градиентом существует связь  42. Векторное поле. Примеры. Векторные линии Опр. Если в каждой точке M пространственной области Ω задан определённый вектор а=вект а(М), то говорят, что в этой области задано векторное поле. Векторное поле задаётся тремя скалярными функциями, являющимися проекциями вектора a(M) на координатные оси ДСК:  Опр. Векторной линией поля вект а называется такая линия, касательная каждой точки которой направлена вдоль заданного в этой точке вектора поля. Уравнение векторной линии:  Примеры векторных полей: электростатическое поле, магнитное поле 43. Поток векторного поля. Формулы для вычисления потока Опр. Поверхностный интеграл 1 рода по поверхности Ω от скалярного произведения вект а на единичный вектор нормали называется потоком векторного поля через ориентированную поверхность   Пример вычисления: Вычислить поток векторного поля  через S – верхняя граница x+y+z=1, расположенного в 1 октанте      44. Дивергенция векторного поля. Векторная запись формулы Остроградского – Гаусса Дивергенция векторного поля – предел отношения потока поля через замкнутую поверхность S, окружающую тело M, к объёму V тела, ограниченного этой поверхностью, при стремлении диаметра d тела к нулю:  Теорема Остроградского-Гаусса в векторной форме Теорема: Для любой замкнутой области V, ограниченной замкнутой поверхностью S, верно равенство:  45. Работа и циркуляция векторного поля Опр. Работа векторного поля вект a вдоль дуги L – криволинейный интеграл 2 рода от скалярного произведения   Если путь интегрирования – замкнутый контур, то работа называется циркуляцией  46. Ротор векторного поля. Векторная запись формулы Стокса Ротором или вихрем векторного поля  называется вектор вида Формула Стокса в векторной форме  47. Векторные дифференциальные операции второго порядка Оператор Гамильтона – с его помощью можно представить градиент, ротор и дивергенцию одновременно  1.  2.  3.  4.  5.  48. Специальные векторные поля а) Соленоидальное, если div вект a=0 б) Потенциальное, если rot вект a=0 и существует функция u такая, что вект а=grad u в) Гармоническое, если rot вект a=0 и div вект а=0 г) Произвольное, если rot вект a≠0 и div вект а≠0 |