Вопросы к экзамену по высшей математике 3 семестр. Матан_3семак. 1. Числовые ряды. Определение сходимости. Необходимое условие сходимости числового ряда
 Скачать 343 Kb.
|
  Опр. ТрР, коэффициенты которого определяются по формулам из теоремы, называется рядом Фурье для функции y=f(x), а его коэффициенты называются коэффициентами Фурье для функции y=f(x) 18. Теорема Дирихле Теорема: Пусть 2π-периодическая функция y=f(x) удовлетворяет: 1) f(x) кусочно-непрерывна на [-π; π], т.е. имеет конечное число точек разрыва первого рода 2) f(x) кусочно-монотонна на [-π; π] Тогда формальный ряд Фурье функции f(x) сх., причём его сумма S(x) удовлетворяет: 1)  , если – точка непрерывности f(x)2)  , если – точка разрыва f(x)19. Ряд Фурье для 2l-периодических функций. Коэффициенты Фурье Пусть T=2π. Отобразим отрезок [-π; π] на [-l; l]. Тогда     20. Ряд Фурье для чётных и нечётных 2l-периодических функций Если y=f(x) – чётная функция, то она разлагается в РФ только по косинусам  , где   Если y=f(x) – нечётная функция, то она разлагается в РФ только по синусам  , где  Замечание: При нахождении коэффициентов Фурье полезно учитывать  21. Разложение в ряд Фурье функций, определённых в конечном промежутке (0;l) Опр. Периодическим продолжением функции y=f(x) называется функция g(x), которая является периодической и совпадает с f(x) на (0; l) g(x) должна удовлетворять условиям теоремы Дирихле и может быть разложена в ряд Фурье а) периодическое продолжение (повторение графика)  б) чётное продолжение (симметрия относительно Оу)  в) нечётное продолжение (симметрия относительно начала координат)  22. Ряд Фурье в комплексной форме    23. Амплитудный и фазовый спектры сигнала, представленного тригонометрическим рядом Фурье     Опр. Амплитудный спектр функции – совокупность амплитуд  - частота первой гармоники Опр. Фазовый спектр функции – совокупность начальных фаз Периодические функции имеют дискретные, линейчатые, амплитудные и фазовые спектры 24. Амплитудный и фазовый спектры сигнала, представленного рядом Фурье в комплексной форме   амплитуда комплексной гармоники модуль амплитуды  комплексные гармоники  аргумент амплитудыОпр. Совокупность модулей комплексных амплитуд называется амплитудным спектром сигнала, представленного в комплексной форме Опр. Совокупность аргументов комплексных амплитуд называется фазовым спектром 25. Определение двойного интеграла. Его геометрический и физический смысл Опр. Если существует конечный предел интегральной суммы, который не зависит ни от способа разбиения области D на части, ни от выбора точек  в них, то он называется двойным интегралом от функции z=f(x,y) по области D Геометрический смысл: Двойной интеграл численно равен объёму цилиндрического тела, ограниченного сверху графиком функции z=f(x, y), снизу – областью D, сбоку – цилиндрической поверхностью Физический смысл: Двойной интеграл  численно равен массе плоской пластины D с плотностью 26. Свойства двойного интеграла        27. Вычисление двойного интеграла 1 случай. Пусть D – криволинейная трапеция, ограниченная  . Причём и они непрерывны. Такая область называется правильной в направлении оси Оу: любая прямая, параллельная Оу, пересекает область в двух местах. Если построить сечение цилиндрического тела Т плоскостью, которая перпендикулярна Ох, то в сечении будет получена криволинейная трапеция, площадь которой  Тогда объём трапеции будет вычисляться  2 случай. Если D ограничена  . Причём  . Таким образом, D является правильной в направлении Ох. Тогда  Замечания: 1) Если область D правильная в обоих направлениях, то ДИ можно вычислять двумя способами 2) Если область D неправильная, то её разбивают на правильные части 28. Замена переменных в двойном интеграле. Якобиан. Полярная система координат Пусть в ДИ  прямоугольные координаты х и у преобразуются к новым u и vх=х(u,v) у=у(u,v) Если полученные функции имеют в некоторой области D непрерывные частные производные первого порядка и ненулевой определитель (Якобиан)  , то имеет место формула  Переход в ПСК полезен, если область D – круг, кольцо, сектор.  Формула замены переменных  29. Определение тройного интеграла Опр. Если существует конечный предел интегральной суммы  , который не зависит от способа разбиения тела V на части или от выбора в них точек , то он называется тройным интегралом от функции u=f(x,y,z) по области V и обозначается   30. Свойства и вычисление тройного интеграла        Вычисление: Пусть область интегрирования V – тело, ограниченное снизу поверхностью z=z1(x,y), сверху поверхностью z=z2(x,y), причём z1(x,y)≤z2(x,y) – непрерывные функции в области D, проекции тела V на плоскость хОу. Будем считать область V правильной в направлении оси Oz. Тогда  31. Замена переменных в тройном интеграле. Якобиан. Цилиндрическая система координат x=x(u,v,w) y=y(u,v,w) z=z(u,v,w)   Цилиндрическая система координат x=ρ*cos(φ) y=ρ*sin(φ) z=z 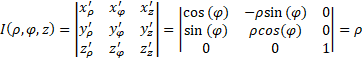  32. Криволинейный интегралы 1 рода. Свойства Опр.  называется криволинейной интегральной суммой 1 рода (по длине дуги)Опр. Предел интегральной суммы, не зависящий ни от способа разбития дуги на части, ни от выбора точек, называется криволинейным интегралом 1 рода от f(x,y) по дуге АВ |