математика ответы. Математика экзамен (вып.). 1. Числовые выражения
 Скачать 0.71 Mb.
|
|
1. Числовые выражения Числовое выражение – это выражение, состоящее одного или нескольких чисел, знаков арифметических действий и скобок. Число тоже является числовым выражением. В процессе выполнения арифметических действий находится значение выражения, но не для всех числовых выражений можно найти значение ( например – 8:(2-2), т.к на 0 делить нельзя ). 2. Числовые равенства и неравенства Числовое равенство – это запись, состоящая из двух числовых выражений, соединённых знаком равенства (5=5, 5+6=7+4, (4:2+5)*3=21). Числовое неравенство – это запись, состоящая из двух числовых выражений, соединённых знаками <, > (неравенства) (5<8, 5+6>4, 4<10-1). Числовые равенства и неравенства бывают верные (5+6=7+4, 4<10-1) и неверные (5+6=7-4, 4+6<10-1). Свойства числовых равенств: 1. К обеим частям истинного числового равенства можно прибавить (вычесть) одно и тоже числовое выражение при этом знак равенства не изменится. Если a=b, то a±c = b±c 2. Если a=b, то a×c = b×c Свойства числовых неравенств: 1. Если a>b, то a–b>0 2. Если a>b, x>y, то a+x > b+y, a–x > b–y 3. Если a>b, то a±c > b±c 4. Если a>b и c>0, то a×c > b×c 5. Если a>b и c<0, то a×c < b×c 3. Выражение с переменной Буквенным выражением или выражением с одной переменной н-ся выражение состоящее из чисел, знаков, арифметических действий , скобок и буквы, которые н-ся переменной 8+0,3в Вместо переменной в выражение можно подставить конкретное значение Множество значений переменных, при которых выражение имеет смысл н-ся областью определения этого выражения (3-у):64 О.О (0…0) (-∞:+∞)( Два выражения с переменной н-ся тождественно равными если при подстановки значения вместо переменной получаются равные значения выражения. 2х+4 2(х+2) Чтобы получить результат используют тождественное преобразование: раскрытие скобок, вынесение общего множителя за скобку, приведение подобных слагаемых, применение формул. 4. Уравнения с одной переменной Уравнение – это равенство 2х выражений с одной переменной. Уравнение с одной переменной это одноместный предикат F1(x)=F2(x) Решить уравнение это значит найти множество значений переменной х, при которых уравнение обращается в истинное равенство или найти множество истинности предиката. Такие значения н-ся корнями уравнения. 7 : Х + 2 = 9 Перед решением уравнения нужно найти ОДЗ. Это множество значений переменной при которых уравнение имеет смысл ОДЗ Х не равно 0 ( - ∞ : 0 ) ( 0 : + ∞ ) Два уравнения называются равносильными, если совпадают ОДЗ и множество решений равны. 5.Неравенства с одной переменной. Предложения 2х + 7 > 10-х, х2+7х < 2, (х + 2)(2х-3)> 0 называют неравенствами с одной переменной. В общем виде это понятие определяют так: Определение. Пусть f(х) и g(х) - два выражения с переменной х и областью определения X. Тогда неравенство вида f(х) > g(х) или f(х) < g(х) называется неравенством с одной переменной. Множество X называется областью его определения. Значение переменной x из множества X, при котором неравенство обращается в истинное числовое неравенство, называется его решением. Решить неравенство - это значит найти множество его решений. Равносильные неравенства. Теоремы о равносильности неравенств В основе решения неравенств с одной переменной лежит понятие равносильности. Определение. Два неравенства называются равносильными, если их множества решений равны. Например, неравенства 2 x + 7 > 10 и 2 x > 3 равносильны, так как их множества решений равны и представляют собой промежуток (2/3, ∞). Теоремы о равносильности неравенств и следствия из них аналогичны соответствующим теоремам о равносильности уравнений. При их доказательстве используются свойства истинных числовых неравенств. Теорема 1. Пусть неравенство f(x) > g(x) задано на множестве Х и h(x) – выражение, определенное на том же множестве. Тогда неравенства f(x) > g(x) и f(x) + h(x) > g(x) + h(x) равносильны на множестве Х. Из этой теоремы вытекают следствия, которые часто используют при решении неравенств: 1) Если к обеим частям неравенства f(x) > g(x) прибавить одно и то же число d, то получим неравенство f(x) + d > g(x) + d, равносильное исходному. 2) Если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части неравенства в другую, поменяв знак слагаемого на противоположный, то получим неравенство, равносильное данному. Теорема 2. Пусть неравенство f(x) > g(x) задано на множестве Х и h(x) – выражение, определенное на том же множестве, и для всех х из множества Х выражение h(x) принимает положительные значения. Тогда неравенства f(x) > g(x) и f(x) × h(x) > g(x) × h(x) равносильны на множестве Х. Из этой теоремы вытекает следствие: если обе части неравенства f(x) > g(x) умножить на одно и то же положительное число d, то получим неравенство f(x) × d > g(x) × d, равносильное данному. Теорема 3. Пусть неравенство f(x) > g(x) задано на множестве Х и h(x) – выражение, определенное на том же множестве, и для всех х из множества Х выражение h(x) принимает отрицательные значения. Тогда неравенства f(x) > g(x) и f(x) × h(x) < g(x) × h(x) равносильны на множестве Х. Из этой теоремы вытекает следствие: если обе части неравенства f(x) > g(x) умножить на одно и то же отрицательное число d и знак неравенства поменять на противоположный, то получим неравенство f(x) × d < g(x) × d, равносильное данному. 6. Уравнения с двумя переменными. Определение. Пусть – выражение с двумя переменными определенное на множестве . Равенство вида , определенное на множестве , называют уравнением с двумя переменными. Областью определения уравнения с двумя переменными является множество . Упорядоченную пару значений переменных обращающую уравнение с двумя переменными в верное числовое равенство, называют решением уравнения с двумя переменными. Пример. Решениями уравнения являются пары . Это уравнение имеет и другие решения. Для нахождения решений уравнения , удобно выразить одну переменную через другую, например, через . Пример. Для нахождения решений уравнения выражают одну переменную через другую, например, через , получают уравнение . Выбрав произвольное значение , вычисляют соответствующее значение . Если , то . Следовательно, пара является решением данного уравнения; если, то, значит, пара так же является решением заданного уравнения и т.д. Множество всех решений уравнения называют множеством решений уравнения. Как правило, уравнения с двумя переменными имеют бесконечное множество решений. Его удобно изображать на координатной плоскости, где все решения уравнения изображают точками на координатной плоскости и получают некоторое множество точек, которые называют графиком уравнения . Так, графиком уравнения является прямая ; графиком уравнения является парабола . Уравнениями с двумя переменными являются уравнения вида: ,– общее уравнение прямой; , – угловой коэффициент, равный тангенсу угла наклона прямой к оси , – ордината точки пересечения прямой с осью ; уравнение окружности вида с центром в начале координат и радиусом ; уравнение окружности с центром в точке и радиусом имеет вид: и др. Для уравнений с двумя переменными справедливы утверждения аналогичные утверждениям для уравнений с одной переменной. 7. Неравенства с двумя переменными. Неравенства вида f(х, у) > 0 или f(х, у) < 0, где f(х; у) - алгебраическое выражение, называется неравенством с двумя переменными. Например: х – 5у < 0, у² - 0,5х +16 ≥ 0, х³+(х - у)² -1>0 Решения неравенств с двумя переменными. Рассмотрим неравенство: (х – у)(х + 2у) > 0. Пара чисел (-3; -1) при подстановке в неравенство обращает его в истинное.(-3–(-1))(-3+2·(-1)) = -2·(-5) =10 > 0 – верно. А пара чисел (5; 10,5) обращает неравенство в ложное. (5 – 10,5)(5 + 2·10,5) = -5,5·26 > 0 – ложно. Пара чисел (-3; -1) является решением данного неравенства, а пара чисел (5; 10,5) – не является решением неравенства. Решением неравенства с двумя переменными называется упорядоченная пара чисел (х; у), которая удовлетворяет этому неравенству, т. е. при подстановке обращает неравенство в истинное. Неравенство с двумя переменными чаще всего имеет бесконечное множество решений. Решить неравенство с двумя переменными, значит найти все его решения или доказать, что решений нет. Для решения неравенств с двумя переменными используется графический метод. Алгоритм решения неравенства с двумя переменными. 1.Построить график уравнения f(х, у) = 0 . Линия графика разбивает плоскость на несколько областей, внутри каждой из которых f(х, у) сохраняет знак. 2. Выбрав произвольную точку, отобрать область (или области), в которых f(х, у) имеет знак, соответствующий знаку исходного неравенства. 3. В случае, если неравенство нестрогое, линия графика включается в решение. Сначала построим прямую. Для этого запишем неравенство в виде уравнения 2у + Зх = 6 и выразим y. Таким образом, получим: y=(6-3x)/2. Эта прямая разбивает множество всех точек координатной плоскости на точки, расположенные выше ее, и точки, расположенные ниже ее.  Возьмем из каждой области по контрольной точке, например А (1;1) и В (1; 3)Координаты точки А удовлетворяют данному неравенству 2у + Зх < 6, т. е. 2 • 1 + 3 • 1 < 6. Координаты точки В не удовлетворяют данному неравенству 2∙3 + 3∙1 < 6. Так как данное неравенство может изменить знак на прямой 2у + Зх = 6, то неравенству удовлетворяет множество точек той области, где расположена точка А. Заштрихуем эту область. Таким образом, мы изобразили множество решений неравенства 2у + Зх < 6. 8. Системы уравнений с двумя переменными. Система уравнений с двумя переменными — это два и более уравнений с двумя неизвестными, записанными одно под другим Решить систему уравнений методом подстановки {2x+y=15 3x−y=5 Решим систему методом подстановки: выразим y из второго уравнения и подставим в первое уравнение. Подставим x в первое уравнение и найдем y:  Ответ: (4;7). Решить систему методом сложения: {x−y−4=0 3x+y−8=0 Решение:  Ответ: (3;−1). 9. Системы неравенств с двумя переменными. Решением неравенства с двумя переменными называется пара значений переменных, обращающие данное неравенство в верное числовое неравенство. Определение: Решением системы неравенств называются пара значений переменных, обращающая каждое неравенство системы в верное числовое неравенство. Изобразим на координатной плоскости множество решений системы неравенств:  Найдём множество решений первого неравенства:  Изобразим график:  Решением будет множество точек расположенных ниже прямой. Найдём множество решений второго неравенства:  Изобразим график уравнения:  Решением будет множество точек расположенных ниже прямой. Изобразим множества решений неравенств в одной координатной плоскости:  Видим их общие решения, которые являются решением системы неравенств. 10. Совокупности уравнений с двумя переменными. Несколько уравнений образуют совокупность уравнений  , если ставится задача найти все те решения, которые удовлетворяют хотя бы одному уравнению совокупности и входит в область определения остальных уравнений.Система двух линейных уравнений с двумя неизвестными имеет вид:  (16)  . Геометрически, каждому уравнению системы (16) соответствует прямая линия на плоскости:  и  Справедливы утверждения: 1) если  , то система (16) имеет единственное решение (геометрически – прямые  пересекаются в определенной точке);2) если  , то система (16) не имеет решений (прямые параллельны);3) если  , то система (16) имеет бесконечно много решений (прямые  и  – совпадают).Основными методами решения систем уравнений (15) являются: 1) метод подстановки; 2) метод исключения неизвестной; 3) метод сложения; 4) метод умножения (деления) уравнений; 5) метод замены переменных; 6) графический метод. 11. Совокупности неравенств с двумя переменными. Совокупность неравенств – это запись, представляющая собой несколько записанных одно под другим неравенств, объединенных слева квадратной скобкой, и обозначающая множество решений, являющихся решениями хотя бы одного из неравенств совокупности. Это определение находится в согласии с описанием совокупностей неравенств, приведенным в учебнике Мордковича [1, с. 222]. Вот пример совокупности неравенств  .При описании совокупностей при надобности можно уточнять число составляющих их уравнений и неравенств, число переменных и вид уравнений и неравенств. К примеру, совокупность из предыдущего абзаца – это совокупность двух неравенств с одной переменной x, причем составляющие ее неравенства – целые рациональные первой степени. Под знак совокупности можно поместить не только уравнения или неравенства по отдельности. Есть смысл рассматривать, например, совокупность уравнения и двух неравенств, неравенства и системы уравнений, совокупность двух систем неравенств и т.п. При этом главное сохранять смысл, заключающийся в совокупности, - она означает множество решений, являющихся решением хотя бы одного объекта совокупности. Для примера приведем совокупность двух систем неравенств  и совокупность такого вида  .Решением совокупности с двумя, тремя и большим числом переменных называется двойка, тройка и т.д. значений переменных, являющаяся решением хотя бы одного объекта совокупности. В качестве примера рассмотрим следующую совокупность 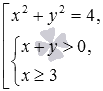 . Пара значений (3, 0) есть решение этой совокупности, так как она является решением системы  , потому что 3+0>0 и 3≥3 - верные неравенства. А пара значений x=−1, y=2 не является решением совокупности, так как она не является решением ни уравнения x2+y2=4, ни системы неравенств .Иногда используются термины «частное решение совокупности» и «общее решение совокупности». Под частным решением совокупности понимают одно отдельно взятое решение, а общим решением называют множество всех частных решений совокупности. Но чаще говорят просто о решении совокупности, а уже из контекста черпают дополнительную информацию, о частном или об общем решении идет речь. В заключение заметим, что из определения совокупности и ее решений следует такой вывод: решение совокупности есть объединение решений всех элементов, составляющих совокупность. А решение систем, напомним, есть пересечение решений всех ее элементов. 12. Обоснование аксиоматического метода построения математических теорий. Аксиоматическое определение множества целых неотрицательных чисел. При аксиоматическом способе построения какой-либо математической теории соблюдаются следующие правила: Некоторые понятия теории выбираются в качестве основных и принимаются без определения. Формулируются аксиомы, которые в данной теории принимаются без доказательства, в них раскрываются свойства основных понятий. Каждому понятию теории, которое не содержится в списке основных, даётся определение, в нём разъясняется его смысл с помощью основных и предшествующих данному понятию. Каждое предложение теории, которое не содержится в списке аксиом, должно быть доказано. Такие предложения называют теоремами и доказывают их на основе аксиом и теорем, предшествующих рассматриваемой. Из правил аксиоматического построения теории выделяют четыре шага: Первый шаг: Задаётся некоторое множество первичных понятий (терминов). Второй шаг: Выделяется некоторое подмножество высказываний (аксиом) о первичных понятиях. Третий шаг: При помощи первичных понятий даются определения всех остальных понятий. Четвёртый шаг: Вывод утверждений (теорем) о первичных и определяемых понятиях. Таким образом, выстраивается алгоритм аксиоматического построения теории: Первичные понятия. Аксиомы. Определения. Теоремы. Соответственно можно на примерах рассмотреть какое утверждение в математике относится к одной составляющей из выше приведенного списка. Примеры первичных понятий. К первичным понятиям аксиоматического построения геометрии на плоскости относятся: точка, прямая, плоскость. Примеры аксиом. Аксиома 1. Через любые две точки можно провести прямую, и притом только одну. Аксиома 2. Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна. Примеры определений. Определение 1: Высказывания, данные через первичные неопределяемые понятия или через некоторые другие ранее известные утверждения, называются определениями. Определение 2: Утверждения, принимаемые без доказательства как верные, называются аксиомами. Определение 3: Новые утверждения о первичных и определяемых понятиях, выведенные чисто логическим путем на основе аксиом, ранее выведенных утверждений и определений, называются теоремами. Определение 4: Простым числом называется такое натуральное число, больше единицы, которое имеет только два делителя – единицу и само это число. Примеры теорем. Теорема 1. Если частное натуральных чисел существует, то оно единственно. Теорема 2. Диагонали у прямоугольника равны. Если построение теории осуществляется аксиоматическим методом, по названым выше правилам, то говорят, что теория построена дедуктивно. При аксиоматическом построении теории, по существу все утверждения выводятся путем доказательства из аксиом. Главным требованием к системе аксиом является ее непротиворечивость, чтобы, сделав вывод теорем на основе этих аксиом, доказанные теоремы не противоречили друг другу. Система аксиом должна быть полной и независимой, При аксиоматическом построении одной и той же теории можно использовать разные системы аксиом. Но они должны быть равносильными. Кроме того, при выборе той или иной системы аксиом математики учитывают, насколько просто и наглядно могут быть получены доказательства теорем в дальнейшем. Большинство интерпретаций для математических теорий (в частности, для арифметических) строятся на базе теории множеств. Поэтому очень важно, чтобы теория множеств была непротиворечивой. Аксиоматическая теория основных структур математики является инструментом, с помощью которого раскрывается теоретико-множественный смысл каждого понятия. Аксиоматическое построение системы натуральных чисел было проведено итальянским математиком Джузеппе Пеано [6] (конец XIX в). Мы сформулируем аксиомы Пеано для расширенного нулем натурального ряда, т.е. для множества N0 = {0, 1, 2, 3, ... } целых неотрицательных чисел. За основное исходное понятие при построении аксиоматической теории принимают отношение: «число в непосредственно следует за числом а», которое обозначается в =  , а также понятия «нуль», «натуральное число».За основные свойства этих понятий принимают следующие аксиомы, обозначенные ниже (А1), (А2), (A3), (А4): (А1). Множество N0 содержит целое неотрицательное число 0, которое не следует ни за каким целым неотрицательным числом. Символически (А1) запишется так: N0) [а' = 0].(А2). Для любого целого неотрицательного числа существует одно и только одно непосредственно следующее за ним натуральное число. Символически (А2) запишется так: (" a Î N0) ($! в Î N) [в = а']. (A3). Для любого целого неотрицательного числа а, отличного от 0, существует единственное целое неотрицательное число, за которым непосредственно следует а. Символически (A3) запишется так: (" a Î N0, a ¹ 0) ($! в Î N0) [в¢ = а]. (А4). (Аксиома индукции). Если подмножество М множества N0содержит 0 и вместе с каждым числом а содержит непосредственно следующее за ним число а', то подмножество М совпадает со всем множеством N0. Символически (А4) запишется так: (0Î М Ù ("a) [а Î М Þ а' Î М]) Þ М = N0. Аксиомы (А1-A3) показывают, что в множестве есть самое первое число («начальный» элемент), а именно 0 и что в нем целые неотрицательные числа идут одно за другим. Аксиома (А4) исключает возможность появления «лишних» элементов в заданном множестве. Нам известна графическая трактовка отношений (Гл. II § 2): если aRв, т.е. если элементы а и в находятся в отношении R, то на графе это обозначается следующим образом а → в. Такая же трактовка на графах и для отношения «непосредственно следовать за». Аксиомы Пеано выделяют из всего многообразия «цепочек» – «цепочки» только одного вида: Принципиально другой модели для приведенной системы аксиом предложить нельзя. Таким образом, мы сформулировали аксиоматическую теорию N0. 13. Метод математической индукции. Одним из самых важных методов математических доказательств по праву является метод математической индукции. Подавляющее большинство формул, относящихся ко всем натуральным числам n, могут быть доказаны методом математической индукции (к примеру, формула суммы n первых членов арифметической прогрессии  , формула бинома Ньютона  и т.п.). |